一类四阶强阻尼波动方程的混合元误差估计

于艳红 刘 洋 李 宏

（1.山东英才职业技术学院 基础部，济南 250116；2.内蒙古大学 数学科学学院，呼和浩特 010021）

本文研究如下一类半线性四阶强阻尼波动方程［1－2]

式中，Ω是R2中具有Lipschitz连续边界∂Ω的有界区域，J＝（0，T]，0＜T＜∞，其中函数f（u）是足够光滑的，且关于u满足Lipschitz连续性条件：也即存在L＞0，使得

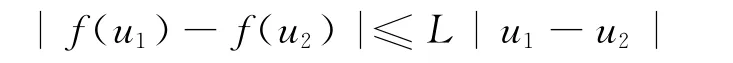
系数A（x）是有界的正函数，即存在正常数m和M满足以下不等式

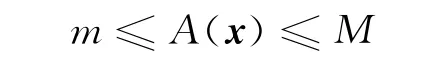
并且假设初值函数u0，u1，边值函数g都是足够光滑的.

近年来，混合有限元方法方面的研究得到了足够的重视，文献［3－5]中使用传统标准的混合元方法分别研究椭圆问题、抛物问题和一些非线性发展方程问题，文献［6]研究了二阶线性强阻尼波动方程的混合有限元方法.文献［2]讨论了四阶强阻尼波动方程一维和多维情形的新的H1－Galerkin混合格式，还给出了有限元解的存在唯一性的证明，并给出了误差估计.但是对于半线性四阶强阻尼波动方程的标准混合有限元方法的研究还没有出现过.本文利用文献［6]的思想提出了半线性四阶强阻尼波动方程的一种混合有限元格式，并分别给出了相应的投影，引理和误差估计证明.

为了下面分析问题需要，首先给出一些必要的定义及记号.（·，·）和‖·‖分别定义为L2内积及范数.并且定义加权L2（Ω）＝（L2（Ω））2范数‖·‖A为‖v‖A＝（A－1v，v）1／2，v∈（L2（Ω））2.并且L2（Ω）的子空间H（div；Ω）如下定义的

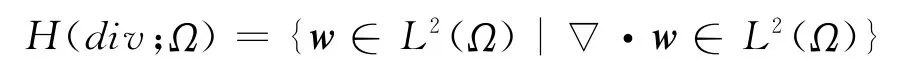
相应的范数定义为

1 混合格式和重要引理

令σ＝A（x）（▽utt＋▽ut＋▽u），可将原方程化为如下一阶系统：

令V＝H（div；Ω）和W＝L2（Ω），下面给出混合有限元的弱形式，求｛（u），σ｝：［0，T]→W×V使得：

其中〈·，·〉是定义在L2（∂Ω）的内积和v是∂Ω的外法向量.

本文使用 Riviart－Thomas空间［4]Vh×Wh⊂V×W，问题（4）～（5）的半离散混合有限元格式为：求｛σh，uh｝：［0，T]→Vh×Wh，使得

为了用混合有限元方法来研究半线性四阶强阻尼波动方程，应该引入一个适合该方程的混合椭圆投影.求满足：

腌渍方式：在制作脆皮鸡时，先加盐、味精等调味料进行前期腌渍，再加入新鲜的蒜苗和蒜瓣等蔬菜一同腌制，然后再刷脆皮水。

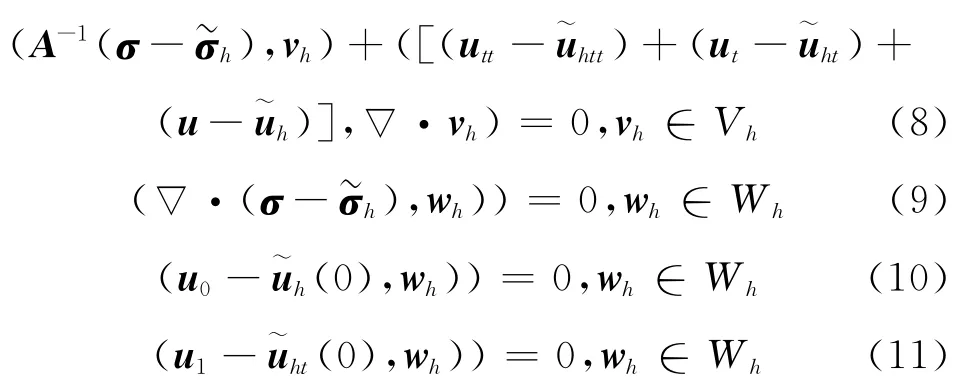
下面给出投影的存在唯一性.

定理1 系统（8）～（9）的解是存在唯一的.

证明 采用文献［6]中的证明方法，只需证明相应的齐次系统

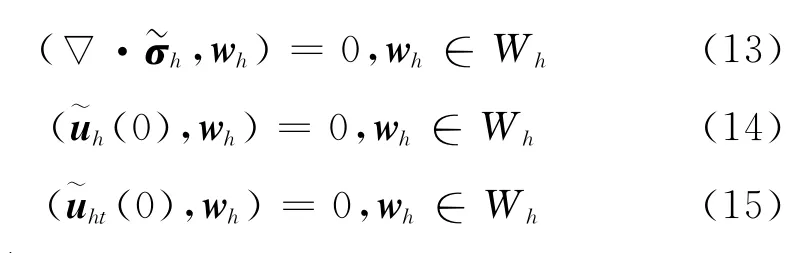
有零解即可.

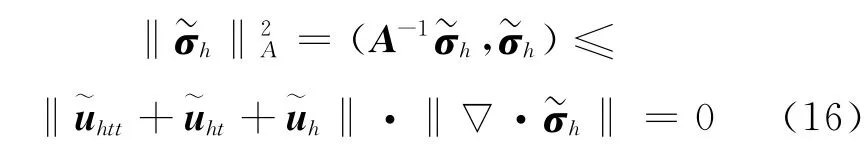
再者，对于空间Wh×Vh，存在一个与h无关的正常数C使得

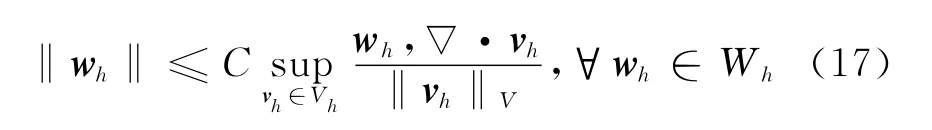
因此由式（12）和式（17），得到

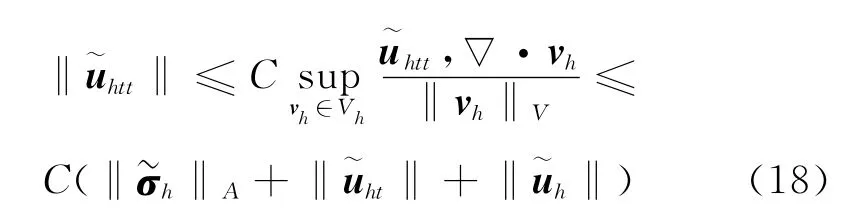
从式（14）和（15）两式，可以得到

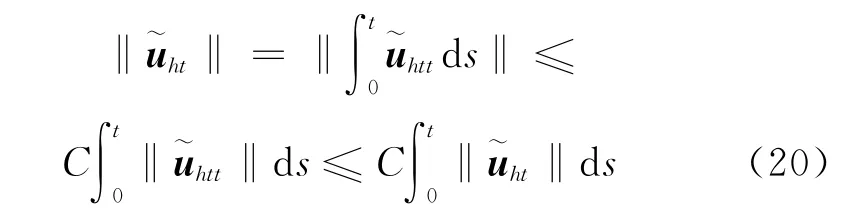
为理论分析的需要，相对于Rviart－Thomas空间，引进投影算子［6]Ph：W→Wh，满足：

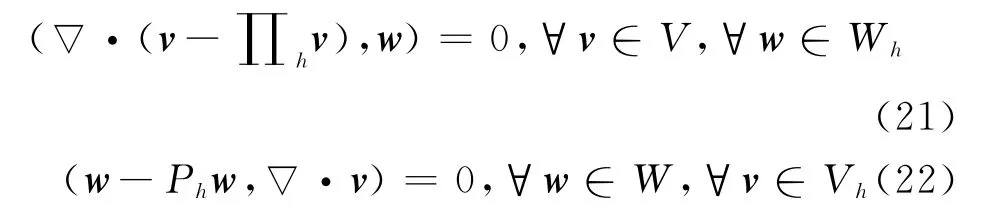
且有逼近性质

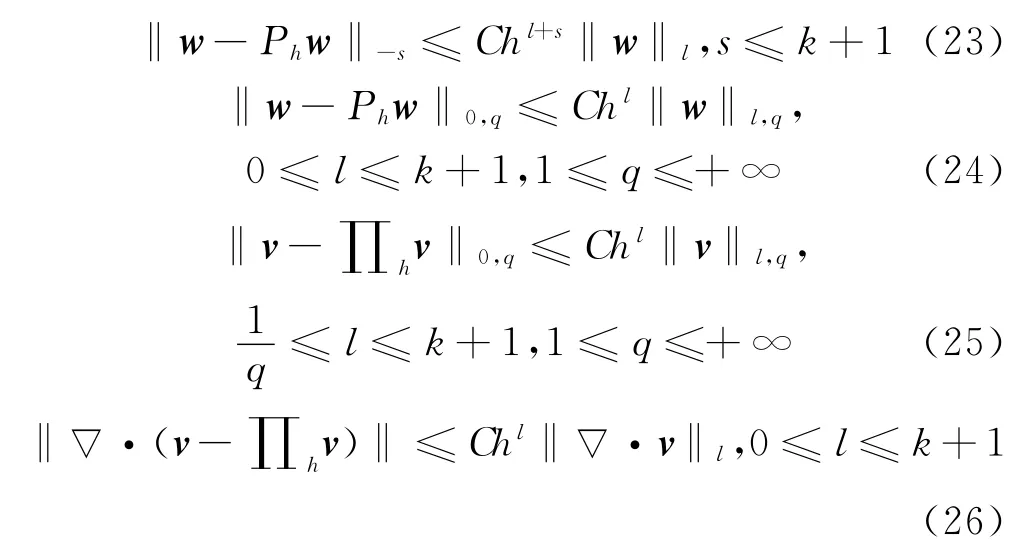
这里Ph是L2投影，∏h是Rviart－Thomas投影.下面给出几个重要的引理.

引理1［6]上面引进的投影算子对∀φ∈V，成立div∏hφ＝Phdivφ（其中div＝▽·）.下面给出的一些误差估计.令u－Phu，则式（8）～（11）可以改写为

引理2 令η＝σ－σh，ρ1＝Phu－uh和ρ2＝u－Phu，满足式（27）～（30），则以下的误差估计成立.

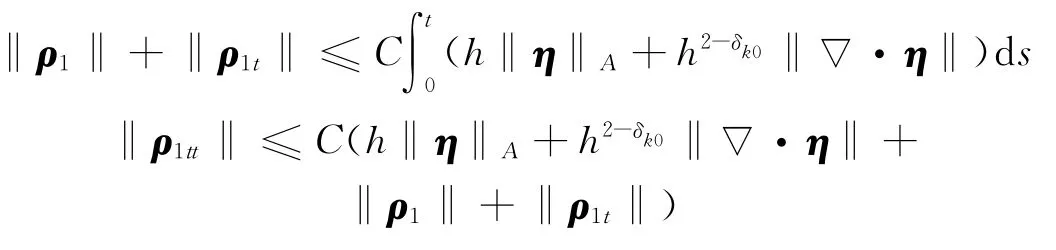
证明 考虑辅助问题

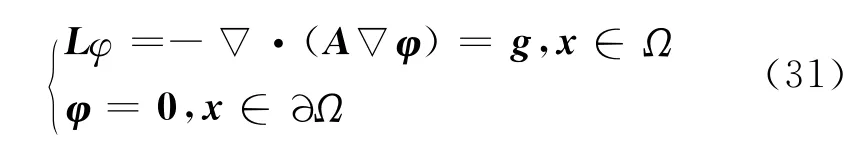
设Ω对问题（31）是2正则，即当g∈L2（Ω）时，存在唯一φ∈H2（Ω）∩H10（Ω）为（31）的解，且有先验估计：

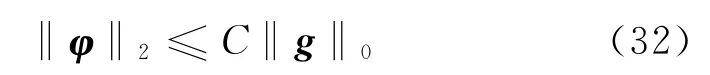
由式（27）和式（31）可以得到

使用已知投影估计及式（28），可得

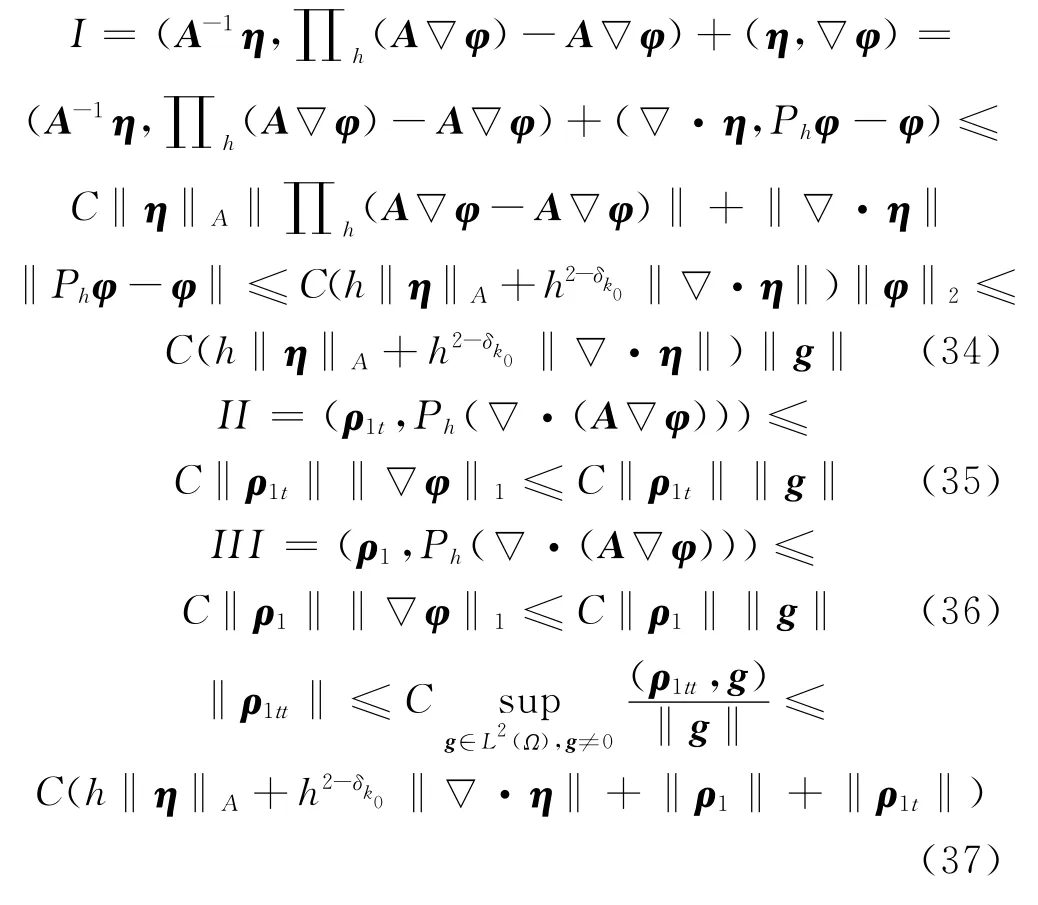
注意到式（29）～式（30），得到

联合式（37）和式（38），使用Gronwall引理，得到

从而有

引理3 令｛σ，u｝和｛σh，uh｝分别是（4）～（5）和（8）～（11）的解，则以下的误差估计成立

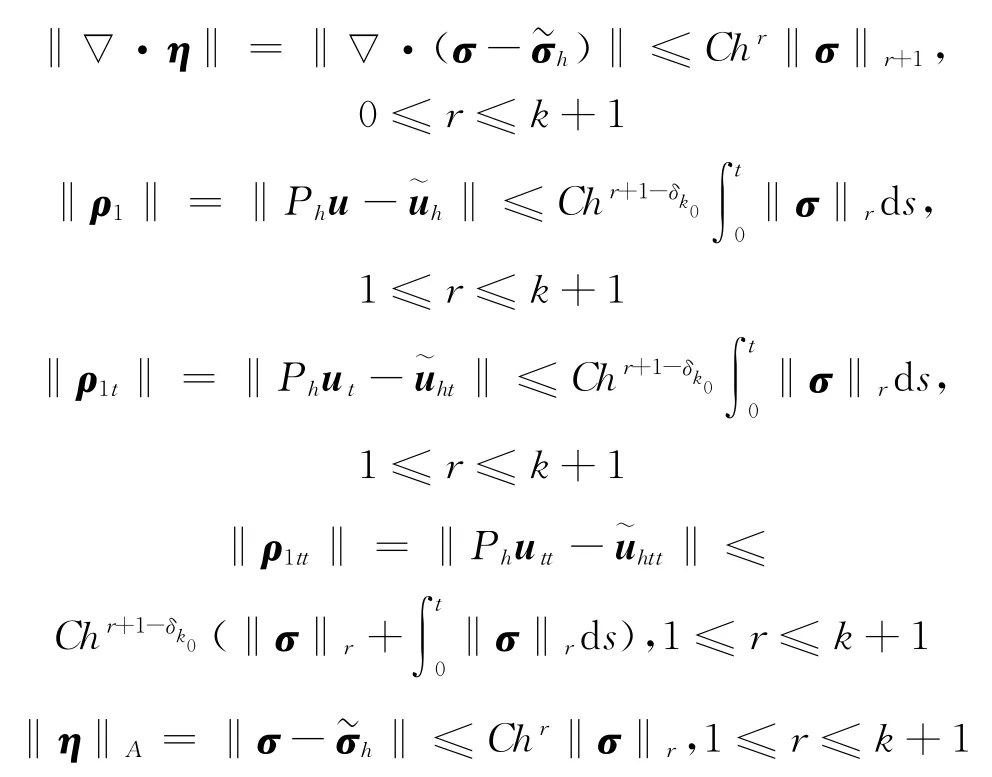
对于k＝0，有

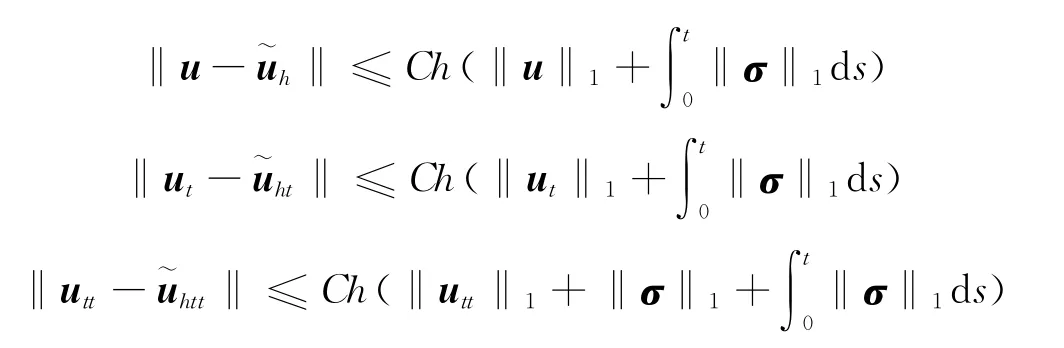
对于k≥1，2≤r≤k＋1，有

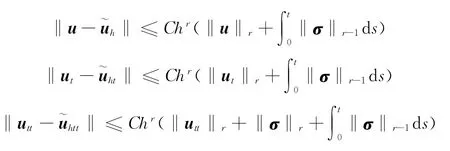
2 误差估计

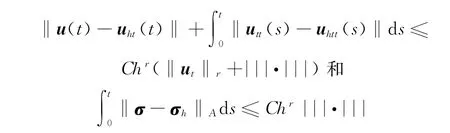
证明 利用ρ和η的定义，将误差写成

因为ρ和η由引理1给定，所以只需估计θ和ζ.因此关于θ和ζ的误差由方程（4）～（9）可以写成

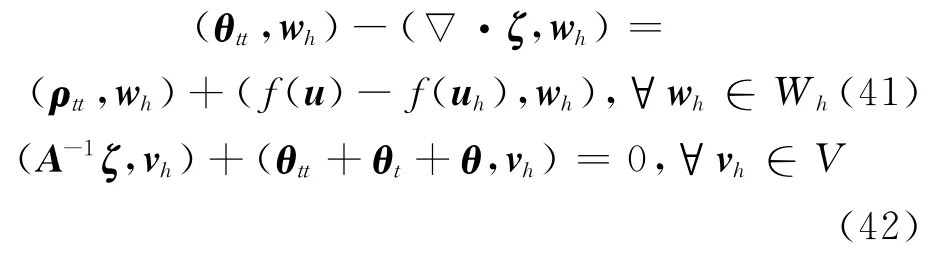
在式（41）中分别取wh＝θtt，wh＝θt和wh＝θ，并将这3个方程相加得

在式（42）中取vh＝ζ，有

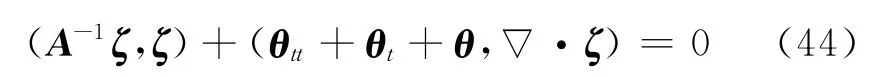
将式（43）和（44）相加，并注意到下面表达式

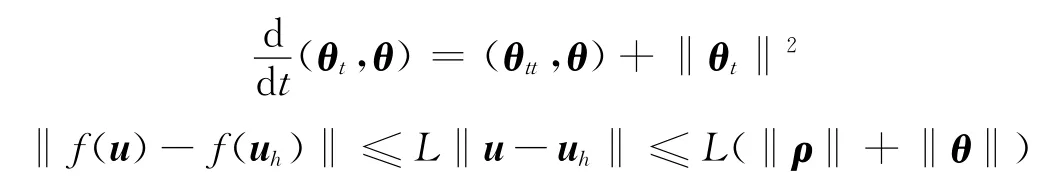
利用Cauchy－Schwarz不等式及Young不等式，有

对上式两端关于时间从0到t积分，得到

再者，由于uht（0）＝Phu1，从而有

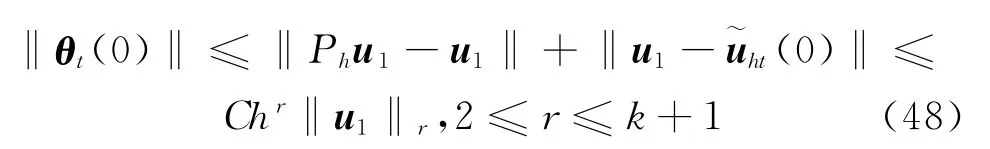
联立式（46）～（48），并使用Gronwall引理可得

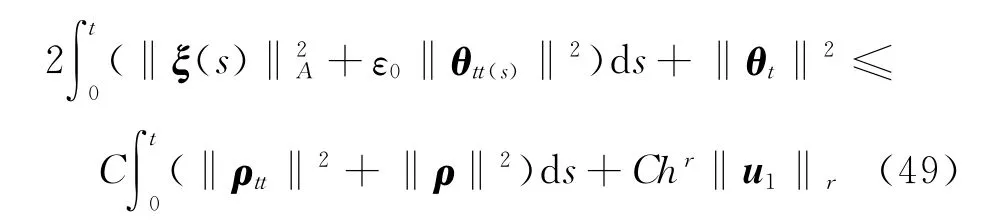
联立式（47）和式（49）使用引理3和三角不等式即得定理2结论.

［1]尚亚东.方程utt－Δu－Δut－Δutt＝f（u）的初边值问题［J].应用数学学报，2000，23（3）：385－393.

［2]刘 洋，李 宏.四阶强阻尼波方程的新混合元方法［J].计算数学，2010，32（2）：157－170.

［3]罗振东.混合有限元方法基础及其应用［M].北京：科学出版社，2006.

［4]Chen Z X.Finite Element Methods and Their Applications［M].Berlin：Springer－Verlag，2005.

［5]Johnson C，Thomee V.Error Estimates for Some Mixed Finite Element Methods for Parabolic Problems［J].RARIO Numer.Anal.，1981，15：41－78.

［6]Pani A K，Yuan J Y.Mixed Finite Element Methods for a Strongly Damped Waveequation［J].Numer.Methods Partial Differential Eq.，2001，17：105－119.