含有未知参数的广义Lorenz系统的自适应投影同步

胡千里 李大美

（1.清华大学 数学系，北京 100084；2.武汉大学 数学与统计学院，武汉 430072）

混沌同步在物理，化学以及保密通讯，生物信息等方面有着潜在的广泛应用［1－5].人们已经提出一系列不同的同步概念，如完全同步，相同步，滞后同步，广义同步等等［6－9]；同时，许多同步方法也不断被提出，如非线性控制方法［9]，自适应方法［14－15]，线性耦合方法等等.在所有的混沌同步方法中，投影同步是很引人注意的一种同步方法.这种同步方法可以保持一些拓扑性质，如 Lyapunov指数和分形维数［10－12].另一种有趣的方法是自适应同步；最近提出的一种称为自适应投影同步的方法［13－15]，结合了投影同步和自适同步的优势，已引起广泛关注.

本文研究广义Lorenz系统这样一个比较特殊的系统的自适应投影同步问题［16－17].文章的组织安排如下：第2部分简要介绍一下广义Lorenz系统；第3部分和第4部分分别考虑系统参数完全未知和部分未知情形下的自适应投影同步问题.第5部分展示数值仿真结果，最后对本文的成果进行简要总结.

1 广义Lorenz系统

2002年，Celikovsky和Chen提出了广义Lorenz系统（GLS）及其标准型的概念［16]，GLS有如下形式

这里a＞0，b＞0，a，b，c，d为系统参数.

系统（2）是系统（1）的一个特殊形式.另外，在系统（2）中，如果令d＝－1，（2）成为著名的Lorenz系统；如果令c＝d－a，（2）则对应于Chen系统；而当c＝0时，（2）正好是Lü系统；如果取a＝25α＋10，b＝（2）成为统一系统.所以系统（2）包含了经典的Lorenz系统族.下面讨论系统（2）含有未知参数情况下的自适应投影同步问题.

2 参数完全未知情况下的自适应投影同步

令系统（2）为驱动系统，受控的响应系统设计如下

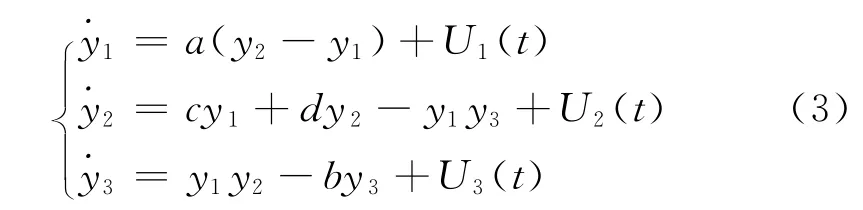
这里，Ui（t）（i＝1，2，3）为控制器，a，b，c，d是未知参数，但是我们假定a＞0，b＞0.

定义系统（2）和（3）的同步误差为：ei＝yi－θxi，（i＝1，2，3），这里θ∈R是尺度因子，可以控制投影比例.可以很容易得到误差系统

设αa，αc，αd是未知参数a，c，d的估计值；k是一个正实数.那么有如下定理：

定理1 对于任意的正实数a，b和任意的实数c，d，如果控制器Ui（t）（i＝1，2，3）设计为如下任意一种形式：

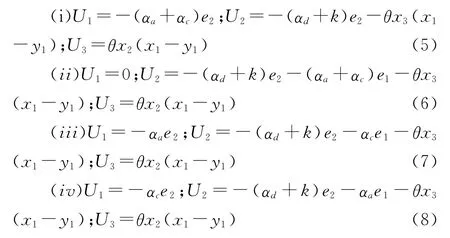
这里αa，αc，αd满足

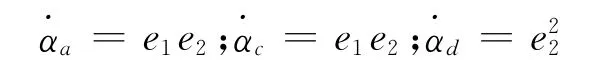
那么系统（2）和（3）对于任意尺度因子θ∈R和任意初值将会实现全局自适应投影同步.

证明：仅以（5）为例，其他的证明过程类似.把（5）代入（4），系统（4）变为

构造如下的Lyapunov函数

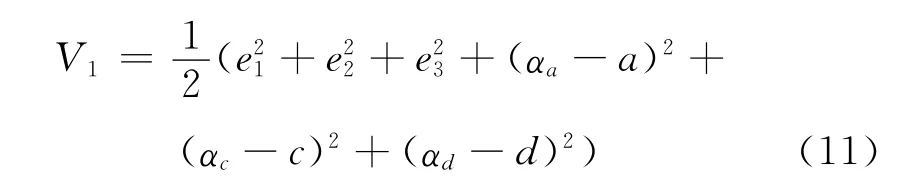
V1沿着系统（10）的全导数为

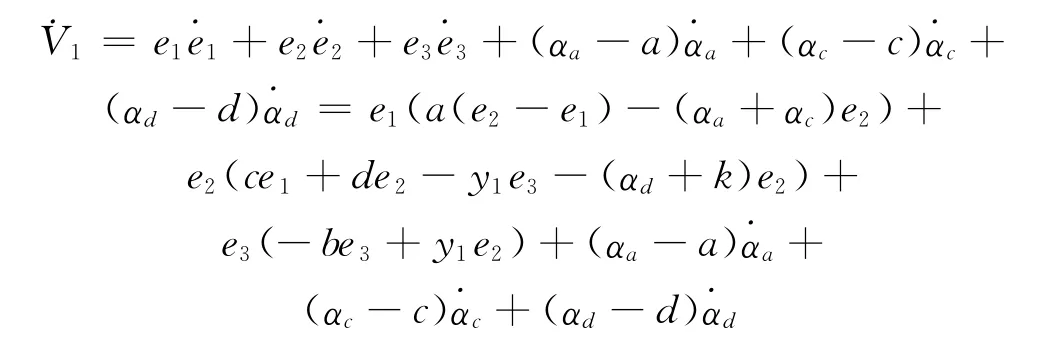
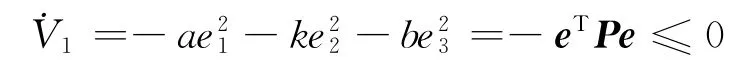
这意味着V1是半负定的.这里e＝（e1，e2，e3）T，P＝diag｛k1，k2，k3｝.

显然，e1，e2，e3，αa－a，αc－c，αd－d∈L∞成立，从误差 系 统 （10），得 到e1，e2，e3∈L∞；再 由V1＝ －eTPe，有

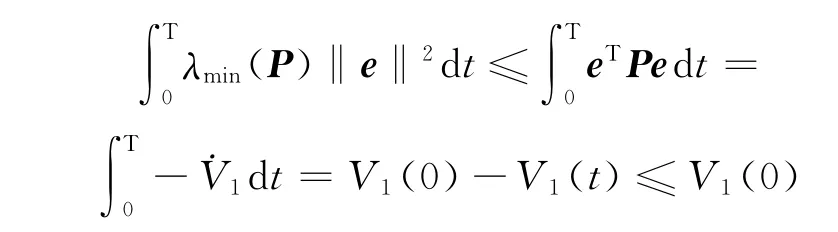
这里λmin（P）是矩阵P的最小特征值.由上式显然可知e1，e2，e3∈L2.因此由 Barbalat引理，我们有当t→∞时，e1（t），e2（t），e3（t）→0.这意味着系统（2）和系统（3）将趋于全局投影同步.

3 部分参数未知情况下的自适应投影同步

仍令（2）作为驱动系统，受控响应系统设计

这里

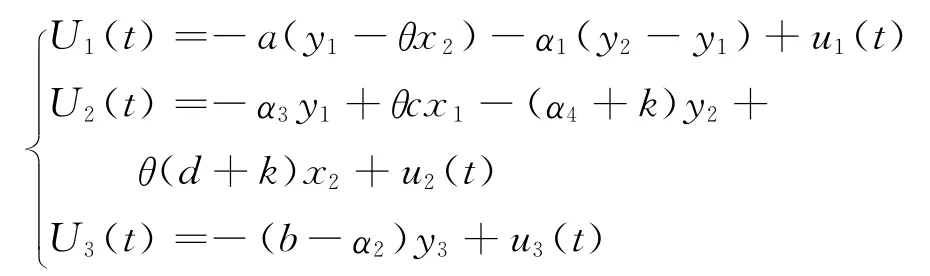
是控制器，a，b，c，d已知，但是ar，br，cr，dr未知.ui是非线性控制器.a，b为正实数；α1，α2，α3，α4是ar，br，cr，dr的估计值；k为任意的一个正数.

定义同步误差ei＝yi－θxi（i＝1，2，3），这里θ∈R仍为尺度因子.很容易得到误差系统

定理2 对于任意的正实数a，b以及任意实数c，d，如果非线性控制器设计为

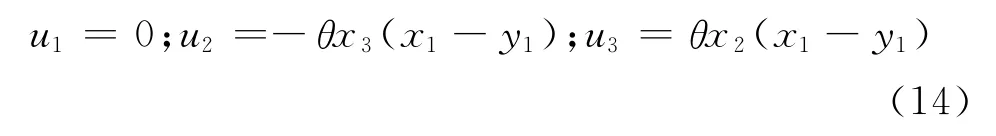
以及自适应率满足

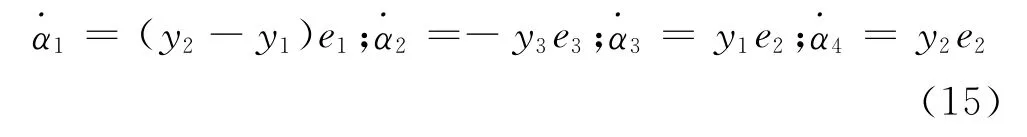
那么系统（2）和（12）将对任意的尺度因子θ∈R实现全局投影同步，同时系统（12）中的未知参数可以被识别出来，更进一步，可以得到＝dr.

证明：构造如下的Lyapunov函数

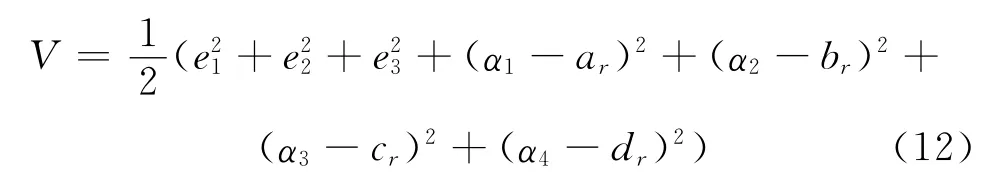
系统（12）沿着系统（13）的全导数为

式中，ui和用（14）和（15）代入，得到

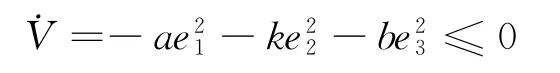
类似于定理1的证明过程，由Barbalat引理，得到t→∞时ei→0.接下来，我们证明（t）＝dr成立.

注1：如果ar，br，cr，dr的选取不同于a，b，c，d，通过定理2可以实现拓扑不等价的两个系统间的同步，在数值模拟部分我们会给出实例.

4 数值仿真

为了验证上述方法的有效可靠性，任取初值（x1（0），x2（0），x3（0））＝（1，4，2），（y1（0），y2（0），y3（0））＝（5，1，－3），（e1（0），e2（0），e3（0））＝Y（0）－θX（0），k＝1进行数值模拟.

4.1 定理1的数值例子

假设未知参数的实际值为：a＝10，b＝8／3，c＝28，d＝－1以及αa，αc，αd的初值为αa（0）＝5，αc（0）＝3，αd（0）＝2，那么系统（2）正是典型的 Lorenz系统，令θ＝－2，驱动响应相图，同步误差的演变曲线图以及自适应率αa，αc，αd的演变图显示在图1中.由图1，我们发现（2）和（3）很快地就实现了投影同步，自适应率收敛到一个常值.

图1 当a＝10，b＝8／3，c＝28，d＝－1及θ＝－2时，驱动响应相图，同步误差的演变曲线图以及自适应率αa，αc，αd演变

图2和图3是另外两个例子.两个例子均说明通过我们设计的控制器可以实现驱动响应系统的自适应投影同步，自适应率均趋于一固定的常数.

图3 当a＝35，b＝3，c＝－7，d＝28及θ＝2时，驱动响应相图，同步误差的演变曲线图以及自适应率αa，αc，αd演变

4.2 定理2的数值例子

取a＝10，b＝8／3，c＝28，d＝－1，假设未知参数的实际值为：ar＝35，br＝3，cr＝－7，dr＝28.对未知参数进行估计的初值设为：α1（0）＝5，α2（0）＝3，α3（0）＝2，α4（0）＝－4，此时系统（2）正是典型的Lorenz系统，（12）是受控的Chen系统.令θ＝4，驱动和响应系统的误差以及参数估计值的演化曲线如图4所示.

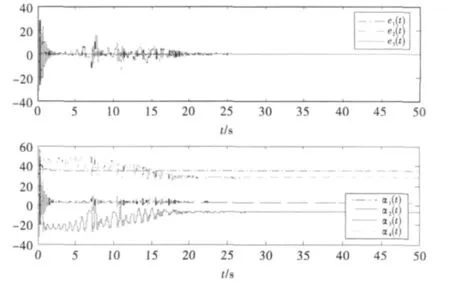
图4 当a＝10，b＝8／3，c＝28，d＝－1及ar＝35，br＝3，cr＝－7，dr＝28，θ＝4时，驱动和响应系统的误差以及参数估计值的演化曲线

从图4可知，系统（2）和系统（12）同样可以很快实现投影同步，也即当t→∞时，yi→4xi，同时我们有＝28.

图5模拟了Chen系统和Lü系统之间的同步.这里a＝35，b＝3，c＝－7，d＝28，未知参数实际值为：ar＝36，br＝3，cr＝0，dr＝20，尺度因子θ＝－2，从图5可以看出，系统（2）和（12）可以很快地实现投影同步，也即当t→∞时，yi→－2xi，同时＝20.也就是说未知参数在同步的同时被识别出来了.

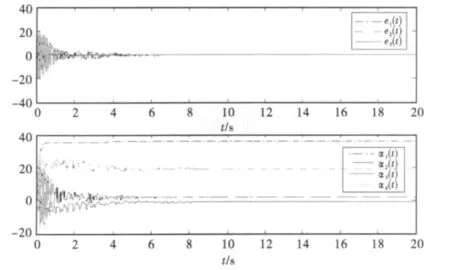
图5 当a＝35，b＝3，c＝－7，d＝28及ar＝36，br＝3，cr＝0，dr＝20，θ＝－2时，驱动和响应系统的误差以及参数估计值的演化曲线

5 结 论

本文研究了广义Lorenz系统的自适应投影同步问题，分别考虑了参数完全未知以及部分未知情形下的自适应投影同步问题，设计了一系列的控制器，这些控制器均可以保证驱动和响应系统实现投影同步.这里的控制器明显比文献［13－15]的简单.这些结论具有广泛应用前景，有望在混沌保密通信等诸多方面得到应用.

［1]Chua L，Itah M.Chaos synchronization in Chua＇s circuits［J].J.Circuits Syst.Comput.，1993（3）：93－108.

［2]Chua L，Yang T，Zhong G.Adaptive synchronization of Chua＇s oscillators［J].Int.J.Bifur.Chaos，1996（6）：189－201.

［3]Chen G，Dong X，From chaos to order.Singapore［M].World Scientific，1998.

［4]Li D，Wang P，Lu J.Some synchronization strategies for a four－scroll chaotic system［J].Chaos，Solitons ＆Fractals，2009，42：2553－2559.

［5]Wang P，Li D，Hu Q.Bounds of the hyper－chaotic Lorenz－Stenflo system［J].Commun.Nonlinear Sci.Numer.Simulat.，2010，15：2514－2520.

［6]Boccaletti S，Kurths J，Osipov G，Valladares DL，Zhou CS.The synchronization of chaotic systems［J].Phys.Rep.，2002，366：1－101.

［7]Rsenblum M，Pikovsky A，Kurths J.Phase synchronization of chaotic oscillators［J].Phys.Rev.Lett..1996，76：1804－1807.

［8]Zhang X，Liao X，Li C.Impulsive control，complete and lag synchronization of unified chaotic system with continuous periodic switch［J].Chaos，Solitons ＆Fractals，2005，26：845－854.

［9]Yang T，Chua L.Generalized synchronization of chaos via linear transformations［J].Int.J.Bifurcation Chaos，1999，9：215－219.

［10]Li C，Chen G.Estimating the Lyapunov Exponents of Discrete Systems［J].Chaos，2004，14：343－346.

［11]Li C，Xia X.On the bound of the Lyapunov exponents for continuous systems［J].Chaos，2004，14：557－561.

［12]Yan J，Li C.Generalized projective synchronization of a unified chaotic system［J].Chaos，Solitons ＆ Fractal，2005，26：1119－1124.

［13]Li R，Xu W，Li S.Adaptive generalized projective synchronization in different chaotic systems based on parameter identification［J].Physics Lett.A ，2007，367：199－206.

［14]Hu M，Xu Z，Adaptive projective synchronization of unified chaotic systems and its application to secure communication［J].Chinese Phys.，2007，16：3231－3237.

［15]Wang D，Han P.Adaptive generalized functional synchronization of chaotic systems with unknown parameters［J].Chinese Phys.B，2008，17：3603－3608.

［16]Celikovsky S，Chen G.On a generalized Lorenz canonical form of chaotic systems［J].Int.J.Bifur.Chaos，2002，12 ：1789－1812.

［17]Wang P，Li D，Wu X，LüJ，Yu X.Ultimate bound estimation of a class of high dimensional quadratic autonomous dynamical systems［J].Int.J.Bifur.Chaos，2011，21：2679－2694.