一类变时滞复杂网络的H∞牵制同步

向 婷 江明辉

（三峡大学 理学院，湖北 宜昌 443002）

近年来，针对复杂网络模型的研究已经深入到生活和科学研究的各个领域，包括互联网、食物链、电力网等，成为目前跨学科、跨领域研究的热点和重点问题之一.所谓复杂网络是由大量节点通过一定的耦合方式连接起来，形成具有复杂动力学行为的大的网络.在不同环境下，这些节点所代表的意义不尽相同，比如在食物链中一个节点表示一个物种，而在互联网中一个节点代表一台独立工作的计算机.同时，节点间的耦合强度和耦合关系对动力行为也会产生不同的促进或抑制作用.

在国内外大量学者研究复杂网络的热潮中，复杂网络的同步问题更是显得非常有吸引力，目前已经得到了大量相关的重要理论结果［1－4].具有代表性的有：Wang和Chen基于简单动力学网络模型的同步问题研究［1－2]；然后Li和Chen又将这个模型扩展到具有耦合时滞的系统［3]，Lv研究了时变动力学网络模型的周期同步［4].这些工作主要集中在对网络同步能力的研究上，侧重于网络属性对网络同步能力的影响，以此通过设计网络的拓扑结构和网络耦合强度来提高网络的同步能力，从而达到实际应用中对网络的要求.而事实上，大部分网络在没有外部控制器的作用下很难实现同步，即便能实现也需要付出较大的代价.因此，同步控制受到广泛关注，一系列的同步控制方法也应运而生.由于复杂网络节点众多，在每个节点施加控制的方法在实际应用中可行性较小，因此有专家学者提出了pinning控制（牵制控制）的思想：通过对网络中的部分节点施加控制从而实现整个网络具有实际所期望的行为［5－8].基于这一理论，复杂网络的控制就有了实际可行的方法.

同时，至目前为止的研究结果大多建立在理想状态下，并没有考虑事实存在而且可能会影响网络动态行为的外部干扰和噪声.因此，提高系统的抗干扰能力显得尤为重要.根据H∞的理论应用，许多相关问题可转变为H∞问题［9－10]，而H∞性能指数恰能精确地反映系统的抗干扰能力.因此，本文将分析具有耦合时变时滞的一般复杂网络的H∞同步问题.

综上所述，本文首先基于pinning控制方法，为一类广义时变时滞复杂网络设计了线性状态反馈控制器，然后基于经典Lyapunov理论［11]和线性矩阵不等式理论［12]，讨论了在这类控制器作用下系统的H∞指数同步控制条件［13]，并给出了相应的算法，最后通过一个经典实例验证了所得结论的有效性和可行性.

1 系统描述与定义

考虑一个由N个相同节点构成的时变时滞复杂网络，其中每一节点均为一个n维动态系统，状态方程描述［1－4]为

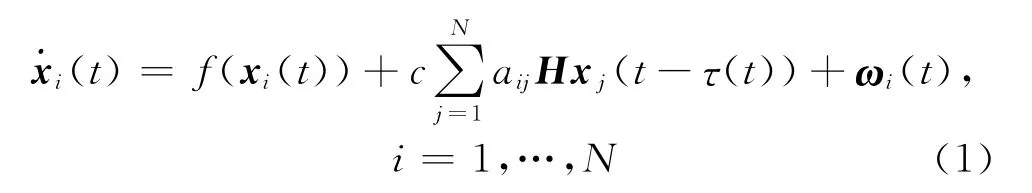
其中，xi（t）＝（xi1（t），…，xin（t））∈Rn为第i个动态节点的状态变量；常数c代表网络的耦合强度；A＝（aij）N×N∈RN×N为外部耦合矩阵，其中aij定义如下：若节点i与节点j（j≠i）存在连接则aij＞0，否则aij＝0，同时A是不可约的.常矩阵H∈Rn×n为内部耦合矩阵.f（xi（t））：Rn×Rn→Rn代表了单个节点的动力学特性，是连续可微向量函数，对于任意初始值（t，xi0）都存在唯一连续解，其中xi0是一个n维向量；ωi（t）∈L0［0，∞）表示不确定外部干扰.时滞τ（t）是一个时变连续函数，满足

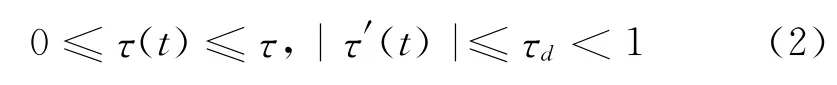
其中τ，τd分别表示时滞和时滞导数的上界.

注1：在网络（1）中，外部耦合矩阵A可以是不对称的，而且矩阵元素也可以不是0或1.同时，对于内部耦合矩阵H没有任何约束条件，这也大大降低了本系统的保守性.

定义1［11]称系统（1）是具有给定H∞性能γ下的鲁棒指数同步，如果满足

1）当外部干扰ω（t）＝0时，系统解s（t）是全局指数同步的，即闭环系统指数稳定；

2）在零初始条件下，对于任意非零外部干扰ω（t）∈L2［0，∞），被控输出满足 ‖z（t）‖2≤γ‖ω（t）‖2.

定义2 函数QUAD（Θ，P）：令P为对称正定矩阵，Θ为对角矩阵，QUAD（（Θ，P））表示一类函数f（x）：RN×n→RN×n，对于任意σ＞0，所有的x，y∈RN×n，t＞t0均满足

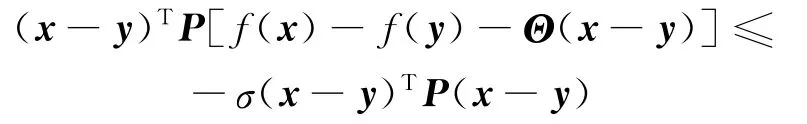
定义3［12]如果存在正常数ε＞0，M＞0，使得对于任意初始条件均满足

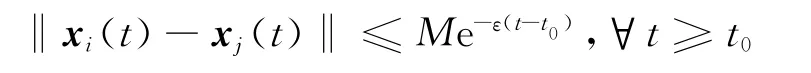
在适当的控制器作用下，原系统（1）是全局指数同步的.

引理1（Schur补）［12]令S11，S12，S22为给定对称矩阵，且满足S22＞0，则

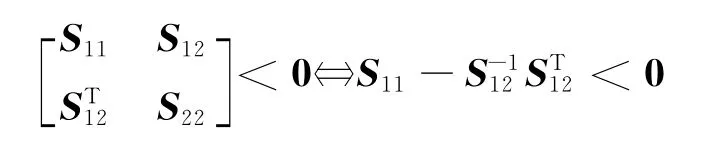
引理2［12]对于任意向量x，y∈Rm，正定矩阵Q∈Rm×m，下述矩阵不等式均成立：

2 主要结果

2.1 连续型复杂网络的H∞指数同步

本文的主要目标是通过引入牵制控制策略使得网络（1）中的每个节点的状态趋于一致，即

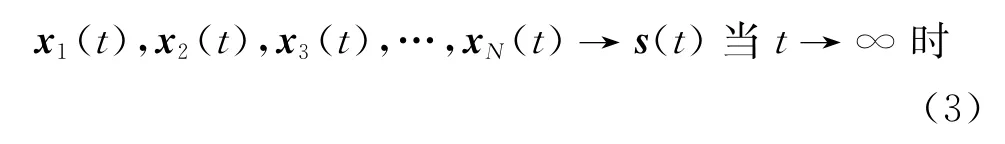
其中s（t）是孤立节点的解，即为此时的同步状态.不失一般性，这里将网络节点进行重新排序，并对前l个节点施加控制［5－8，14].因此，被控系统可描述为

在此，应用时滞状态反馈控制器，具体形式为

其中，反馈增益di≥0，ki≥0.定义误差向量：Δi（t）＝xi（t）－s（t），i＝1，2，…，N.

结合式（1）～（4），若j∈｛l＋1，…，N｝，则令dj＝0，kj＝0.则误差系统可通过非线性微分方程描述为

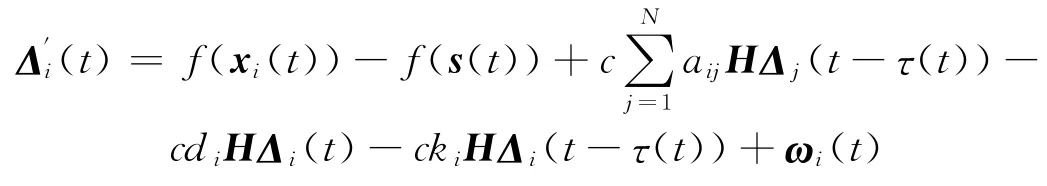
定义如下矩阵：K＝diag（k1，……，kN），D＝diag（d1，…，dN），其中对于任意i∈｛l＋1，…，N｝有di＝ki＝0.在此采用Kronecker积的表示形式，可将误差系统进一步简化为

因此，将N×n维复杂网络（1）的同步控制问题转化成了非线性误差系统（5）的稳定性问题.

同时，为了让系统具有较强的抗干扰能力，定义如下系统输出函数

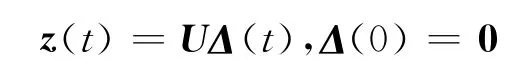
而系统的抗干扰能力可通过闭环传递函数来进行判断［15－16]，函数具体形式为

此时的目的是使得对于任意给定的H∞性能指标γ均有：‖Tωz‖≤γ，即

定理1 若假设条件（2）成立，f（x（t））∈QUAD（（Θ，P）），且对于任意给定的γ＞0，存在一个正常数ε以及对称正定矩阵P，Q满足

其中Γ＝εP－2σP＋2PΘ－2cPE＋eετQ，E＝D⊗H，F＝（A－K）⊗H，则误差系统（5）是指数稳定的，即被控闭环系统（4）是H∞指数同步的，且指数收敛率为

证明：由于E＝D⊗H，F＝（A－K）⊗H，则误差系统（5）可进一步简化为

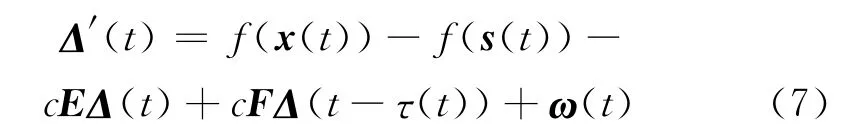
首先，建立系统（7）在ω（t）＝0下的指数稳定性［11，17].选取 Lyapunov函数

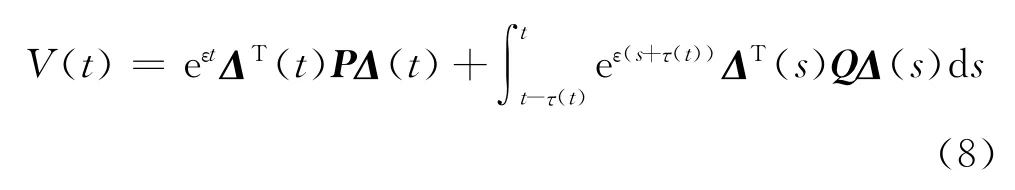
其中P，Q是对称正定矩阵.接下来沿系统（7）的任意轨迹，让V（t）对时间t求导可得

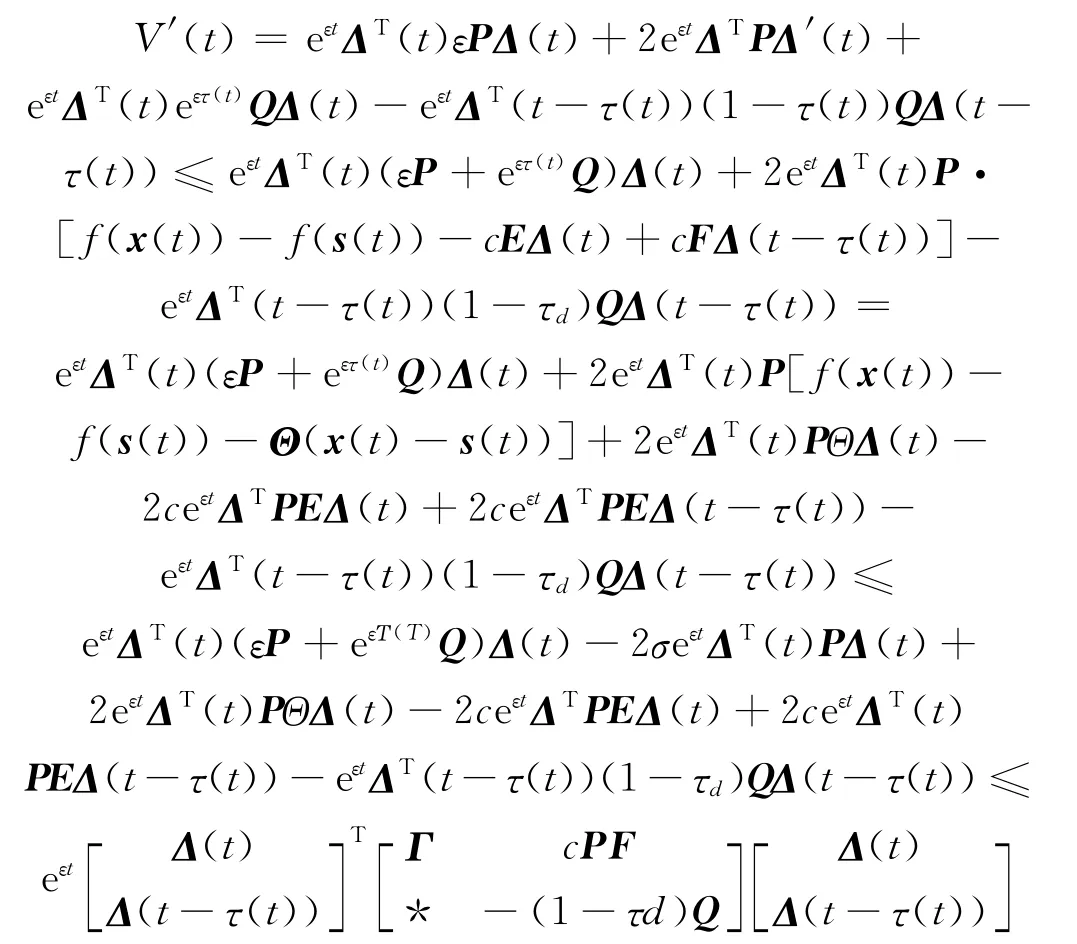
其中Γ＝εP－2σP＋2PΘ－2cPE＋eετQ.因此V（t）≤V（0）.

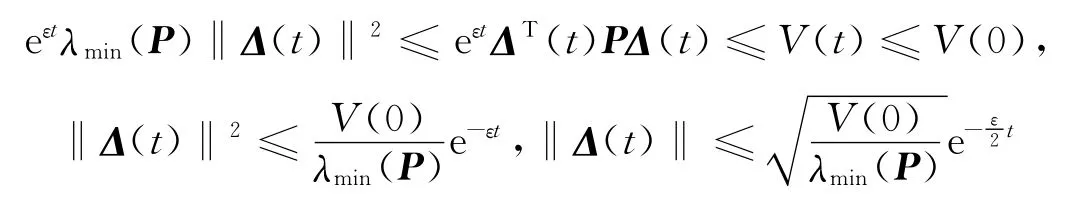
同时，在此结式合（6），（7）和（8），还可得到

其中，

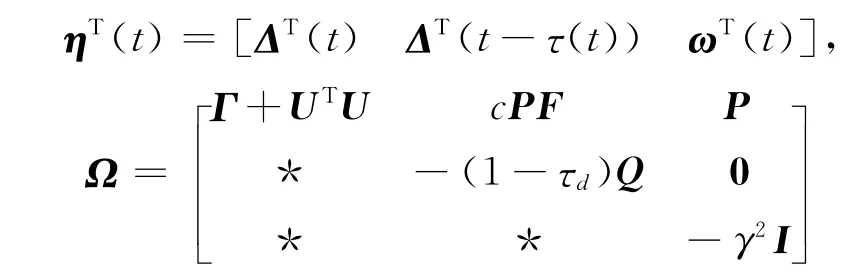
接着应用Schur补引理，可知不等式（6）就等价于：Ω＜0.

因此，

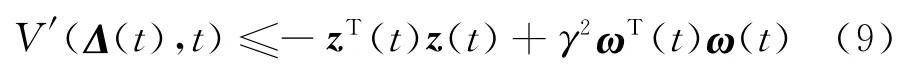
在此，对式（9）的左右两边均从0到t进行积分，则可得到：

令t→∞，则在零初始条件下，有

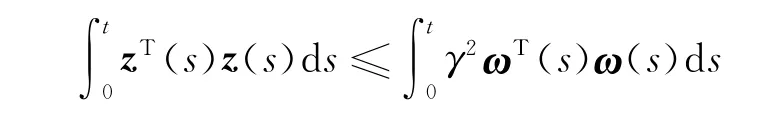
因此，对于任意非零的ω（t）∈L2［0，∞），均有‖z（t）‖2≤γ2‖ω（t）‖2成立.根据定义1，结果得证，定理证明完毕.

定理1将时变时滞复杂网络（1）的H∞指数同步控制问题转化为矩阵P，Q的存在性问题，为进一步简化结论，不妨令Q为单位矩阵Im，可得如下结论.

定理2 若假设条件（2）成立，f（x（t））∈QUAD（Θ，P），且对于任意给定的γ＞0，存在一个正常数ε以及对称正定矩阵P，满足

其中Γ＝εP－2σP＋2PΘ－2cPE＋eετIm，则误差系统（5）是指数稳定的，即被控闭环系统（4）是H∞指数同步的，且指数收敛率为－ε／2.

定理3 当τ′（t）＝0时，若假设条件（2）成立，f（x（t））∈QUAD（Θ，P），且对于任意给定的γ＞0，存在一个正常数ε以及对称正定矩阵P，Q，满足

其中Γ＝εP－2σP＋2PΘ－2cPE＋eετQ＋PFQ－1F－1P－1，则误差系统（5）是指数稳定的，即被控闭环系统（4）是H∞指数同步的，且指数收敛率为－ε／2.

证明：定义Lyapunov函数

其中，P，Q是对称正定矩阵.接下来沿系统（7）的任意轨迹，让V（t）对时间t求导可得

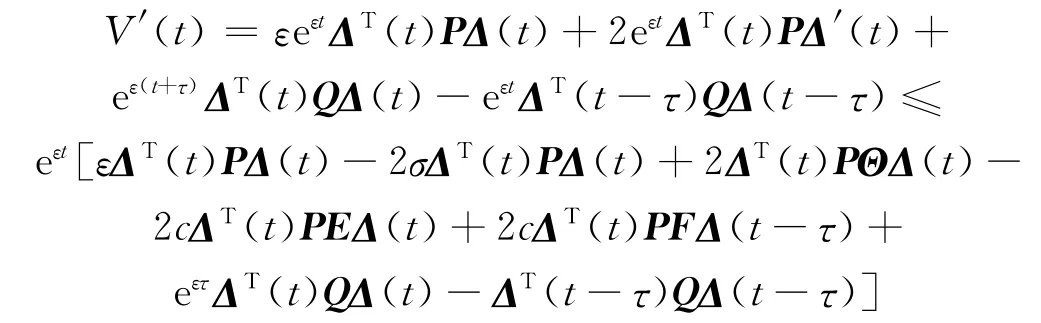
根据引理2，可得

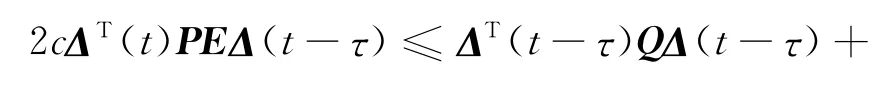
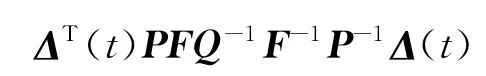
因此，

接下来的论证过程类似于定理（1）的证明，在此省略.

2.2 离散型复杂网络的H∞指数同步

连续型系统可由微分方程来表述，而离散型系统由差分方程描述，两者需要差别对待.在此，本文有必要将所得结论进一步推广到离散型系统［18－21].考虑一个由N个相同节点组成的网络，其中每一节点均为一个n维动态系统，状态方程为

其中xi，f，c，aij，H，ω所代表的意义与系统（1）中相同.时滞τ（k）是一个时变离散函数，满足

本节首先需要考虑的是将系统（1）稳定到同步状态s（k），即

为实现这一目标，本节仍然采用牵制控制策略.为了不失一般性，这里将网络节点进行重新排序，并令前l个节点为受控节点.在此，应用时滞状态反馈控制器，具体形式为

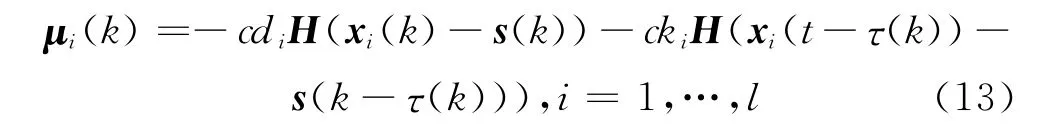
其中，反馈增益di≥0，ki≥0.定义误差系统：Δi（k）＝xi（k）－s（k），i＝1，2，…，N.

结合式（10）～（13），如果j∈｛l＋1，…，N｝，令dj＝0，kj＝0.则误差系统可通过非线性微分方程描述为

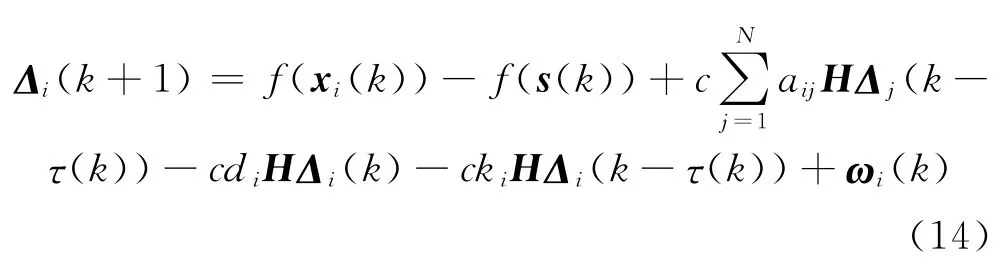
其中对于任意l≤i≤N有di＝ki＝0.

因此，将N×n维系统（10）的同步控制问题转化成了非线性系统（14）的稳定性问题.

同时，为了让系统具有较强的抗干扰能力，定义如下系统输出函数

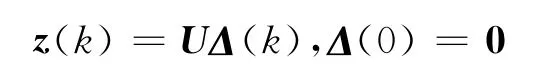
在此的目的是使得对于任意给定的H∞性能指标γ均能有：‖Tωz‖≤γ，即

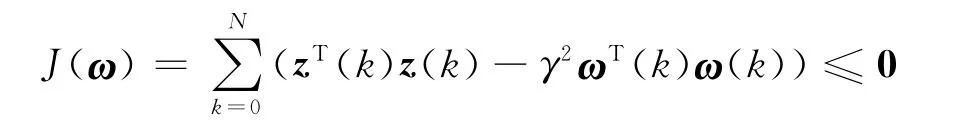
定理4 如果假设条件（11）成立，且对于任意给定标量τm＞0，τM＞0，γ＞0，存在一个正常数ε以及对称正定矩阵P，Q满足

其中Γ＝eε（J－cE）P（J－cE）－P＋Q，则在控制器（13）的作用下，原系统（10）实现H∞指数同步，且指数收敛率为－ε／2.

证明：定义矩阵K＝diag（k1，…，kN），D＝diag（d1，…，dN），并将网络模型在s（k）处线性化，则可将式（4.5）转化为

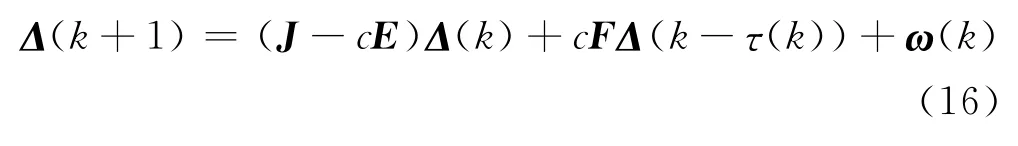
其中J＝diag（J1，…，JN）且是f（x）在s（k）处的Jacobian矩阵，E＝D⊗H，F＝（AK）⊗H.在此，首先建立系统（16）在ω（t）＝0下的指数稳定性.构造如下Lyapunov函数：

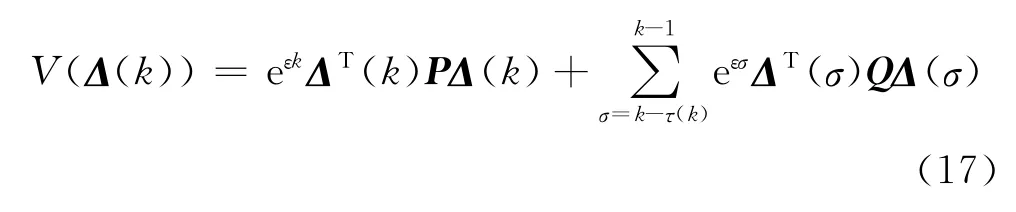
其中P，Q∈RN×n是对称正定矩阵.

其中Γ＝eε（J－cE）P（J－cE）－P＋Q.因此，

下面，需要证明对于任意非零ω（k）∈L2［0，∞），闭环系统（4.6）在零初始状态下满足‖Tωz‖≤γ.这里将Jωz进一步转化为

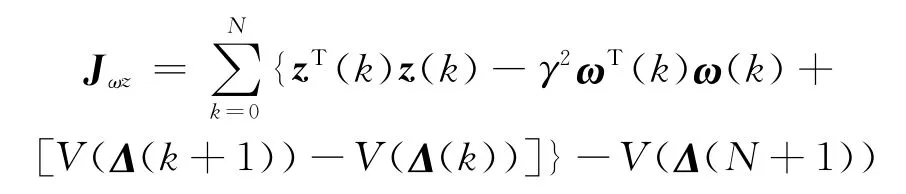
由于V（Δ（k））≥0，容易得到

那么，根据Schur补性质，在零初始状态下，就有‖z‖2≤γ‖ω‖2，定理得证.

定理5：如果假设条件（11）成立，且对于任意给定标量τm＞0，τM＞0，γ＞0，存在一个正常数ε以及对称正定矩阵P满足

其中Γ＝eε（J－cE）P（J－cE）－P＋ceε（J－cE）PF，则在控制器（13）的作用下，原系统（10）实现H∞指数同步，且指数收敛率为－ε／2.

由此可见，由差分方程描述的离散系统在牵制控制下也能实现指数同步.

注2：与文献［7，21]相比，本文结论主要作了几方面的推广：（1）网络系统的结构无需假设aij为0或1，对内部矩阵H也没有约束的条件；（2）在文献［7]中，时滞是一个常数，不随时间的变化而变化，但本文考虑的是时变耦合时滞系统；（3）应用莱布尼兹－牛顿公式和一些自由加权矩阵使得本文的研究结论具有更好的保守性；（4）与文献［7，21]中的渐进同步相比，本文的指数同步具有更快的收敛速度.

注3：本文采用了Pinning控制策略使得具有时变时滞和不确定干扰的复杂网络实现指数同步.此外，在已有文献中，很多研究结论都集中在指数同步问题上，很少考虑到时变时滞复杂网络的H∞指数同步问题.因此，本文恰是对以往研究成果的一个有用推广.

注4：容易看出在定理1，定理4中所叙述的条件关于ε，P，Q都不是严格的线性矩阵不等式，出现了非线性部分.但是，在此一旦固定P，Q，这些条件就可转化为基于优化问题的线性矩阵不等式.

1）估算定理1中ε的最优界：Maximize：ε

Subject to（6）；

2）估算定理4中ε的最优界：

Maximize：ε

Subject to（15）；

为了在后面给出直观的实例分析，在此将具体讨论相应的算法分析.算法描述如下：

步骤1：首先为ε选择一个非负初值，并令N0＝1，k＝0.同时计算终止次数N，然后转到步骤3；

步骤2：若Nk＋1≤N，则令ε＝0.5＊ε，然后继续下一步.否则，计算失败，终止算法；

步骤3：利用Matlab中的LMI工具箱解线性矩阵不等式（6）或（15）.若不可解，则令Nk＋1≤Nk＋1，k＝k＋1，然后转到步骤2.否则，计算P，Q并结束算法.

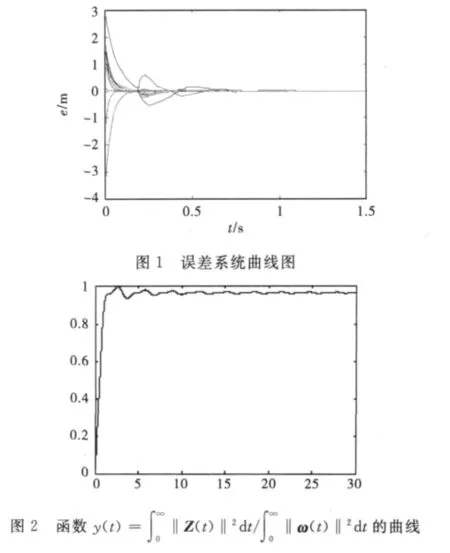
3 仿真实例

本节将通过具体的实例来验证结论的有效性.

考虑一个由4个节点所构成的动力系统，而每个节点代表一个三维子系统.此时系统可记为

例：对于式（19），选择如下：

很显然，函数f（x）满足函数QUAD（Θ，P）的条件.在此，选择第2和第3个节点实施控制，且控制增益选择为d2＝d3＝k2＝k3＝3.根据前面介绍的算法，可计算得到指数同步的最大收敛率为ε≤1.2，同时，通过应用Matlab中的LMI工具箱计算得到存在对称正定矩阵P，Q.

4 结 论

本文主要研究了牵制控制下的时变时滞系统的H∞指数同步问题，基于Lyapunov稳定性理论，并借助于线性矩阵不等式方法给出了时变时滞复杂网络的H∞指数同步控制充分条件，在保证系统具有较好同步性能的同时还保证了系统的抗外部干扰能力，并在实际应用中将H∞指数同步控制问题和指数收敛率的确定问题有效转化为能利用LMI工具箱解决的优化问题，大大提高了该理论在实际应用中的可操作性.最后通过有代表性的实例对所得结论分别进行了验证.

［1]Wang Xiaofan，Chen Guanrong.Synchronization in scale－free dynamical networks：robustness and fragility［J].IEEE Trans.Circuits and System－I，2002，49（1）：54－62.

［2]Wang Xiaofan，Cheng Guanrong.Synchronization in small－word dynamical networks［J].Int.J.Bifurcation，2002，12（1）：1987－1992.

［3]Li Chuanguang，Chen Guanrong.Synchronization in general complex dynamical networks with coupling delays［J].Physica A，2004，343：236－178.

［4]Lv Jinhu，Chen Guanrong.Time－varying complex dynamical network model and its controlled synchronization criteria［J].IEEE Trans.Autom.Control，2005，50（3）：841－846.

［5]Wang Lei，Sun Youxian.Robustness of pinning ageneral complex dynamical network［J].Physics Letters A，2010，374（15）：1699－1703.

［6]Yu Wenwu，Chen Guanrong，Lv Jinhu.On pinning synchronization of complex dynamical networks［J].Automatica，2009，45（2）：429－435.

［7]Liu Z，Chen Z，Yuan Z.Pinning control of weighted general complex dynamical networks with time delay［J].Physica A，2007，375（1）：345－354.

［8]Xu Degang，Su Zhifang.Synchronization criterions and pinning control of general complex networks with time delay［J].Applied Mathematics and Computation，2009，215（4）：1593－1608.

［9]Hamid Reza Karimi，Peter Maass.Delay－range－dependent exponential synchronization of a class of delayed neural networks［J].Chaos，Solitons and Fractals，2009，41（3）：1125－1135.

［10]Lin Peng，Jia Yingmin，Li Lin.Distributed robust consensus control in directed networks of agents with timedelay［J].Systems and Control Letters，2008，57（8）：643－653.

［11]Liao Xiaoxin.Theory methods and application of stabili－ty［M].Wu Han：Huazhong University Press，2010.

［12]Chen Peng，Tian Yuchu.Delay－dependent robust stability criteria for uncertain systems with interval time－varying delay［J].Information Sciences，2008，214（2）：480－494.

［13]Li Yu，Jian Chu.An LMI approach to guaranteed cost control of linear uncertain time－delay systems［J].Automatica，1999，35（6）：1155－1159.

［14]Xiang Linying，Chen Zengqiang，Liu Zhongxin.Pinning control of complex dynamical networks with heterogeneous delays［J].Computers and Mathematics with Applications，2007，379（1）：298－306.

［15]Li Zhongkui，Duan Zhisheng，Huang Lin.Control of networked multi－agent systems［J].Journal of Systems Science and Complexity，2009，22（1）：35－48.

［16]Duan Zhisheng，Zhang Jingxin，Mosca E.Robust H2 and filtering for uncertain linear systems［J].Automatica，2006，42（11）：1919－1926.

［17]Liu Zhongxin，Zhang Xin，Chen Zengqiang，YUAN Zhuzhi.Yuan.Exponential stability criteria for feedback controlled complex dynamical networks with time delay［J].International Journal of Nonlinear Science，2007，7（1）：95－103.

［18]Boukas E K.State feedback stabilization of nonlinear discrete－time systems with time－varying time delay［J].Nonlinear Analysis，2007，66（6）：1341－1350.

［19]Wang Baoxian，Guan Zhihong.Chaos synchronization in general complex dynamical networks with coupling delays［J].Nonlinear Analysis：Real World Applications，2010，11（3）：1925－1932.

［20]Xiong Wenjun，Cao Jinde.Global exponential stability of discrete－time chen－grossberg neural networks［J].Neurocomputing，2005，64：433－446.

［21]Chen Wuhua，Lu Xiaomei，Liang Dongying.Global exponential stability for discrete－time neural networks with variable delays［J].Physics Letters A，2006，358（3）：186－198.