基于数据驱动的多工况过程控制性能评估研究

林晓钟，谢 磊

（浙江大学智能与系统控制研究所工业控制技术国家重点实验室，310027 杭州）

基于数据驱动的多工况过程控制性能评估研究

林晓钟，谢 磊

（浙江大学智能与系统控制研究所工业控制技术国家重点实验室，310027 杭州）

为了解决如何选择合适的基准数据与实时数据进行控制性能评估问题，提出一种基于多变量分类的方法.用一种综合相似因子来衡量当前实时数据和某一工况下数据的相似性，确定实时数据所属的工况，而后再进行控制性能评估，通过仿真结果验证了新方法的有效性.

多工况;相似因子;性能评估

针对基于过程传递函数模型来进行性能评估的不足，近年来学者们提出直接利用过程输出的数据来进行性能评估的方法.基于数据驱动方法最大的优势在于不需要过程知识的精确信息且输出数据较容易获得，从数据中挖掘出过程的信息，因此该类方法具有很强的实用性.Jie Yu等提出了基于数据驱动的性能评估的基准［4－6］，把一段理想的历史输出数据作为参考数据基准，通过分析所监视时段数据和基准时段数据的广义特征值，提出相应的性能优/劣的特征向量.进一步利用统计推断方法得出特征值在相应特征方向上的置信区间，以及在优/劣子空间下的性能指标，从而评价和监视控制性能的优劣.Xuemin Tian［7］等提出了一种基于2－范数的协方差性能基准，通过将当前操作工况数据与基准数据进行比较，从而监控当前控制器的性能变化情况.Gudi［8］等提出了一种基于对应分析的统计基准上的控制器性能评估基准的思想.

然而，以上基于数据驱动的性能评估方法都有一个前提假设:基准数据都来自单一的稳定的工况，而实际生产过程极其复杂，往往不是运行在单一的工况，生产负荷、产品特性、原料组分等的改变，都会导致工况的改变.所以必须考虑到工况变化引起的基准调整问题，即在多工况下历史数据库中有多组可选的数据作为基准，如何选择恰当的基准是较为关键的问题，其关系到性能评估结果的正确与否.本文提出在进行性能评估前，通过分类的方法先确定实时数据所属的工况，从历史数据库中选择恰当工况的数据作为基准，再进行性能评估.采用结合PCA相似因子与几何距离相似因子的多变量分类的方法来衡量两组数据矩阵之间的相似性，从而得到较为准确的分类结果，避免了由于基准数据选择的不恰当影响了控制器性能评估的结果.仿真例子证实了该方法的有效性.

1 基于协方差的数据驱动型的性能评估方法

文献［5］等提出了基于数据驱动的基准.即选取一段控制器性能较为满意的历史数据集I作为基准数据，将需要评估的实时数据作为数据集Ⅱ，定义基于数据驱动的控制器性能评估基准如下:

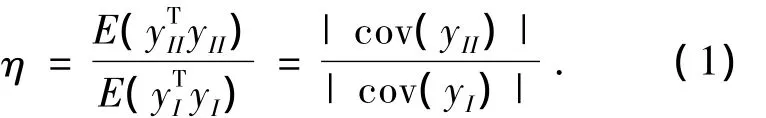
从几何意义上说，|cov(yI)|和|cov(yII)|分别表征由数据集yI和yII的协方差所张成的超曲面的体积;从代数角度，|cov(yI)|和 |cov(yII)|综合考虑了协方差阵整体的因素，而并非单纯地考虑其对角线元素.由分析的结论可知:当η越接近于0时，控制器性能越好;当η越大时，控制器性能越差.通过求解如下优化问题寻找η最大的方向:

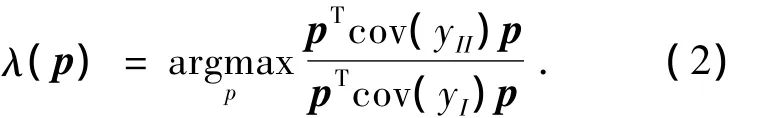
对式(2)求解得

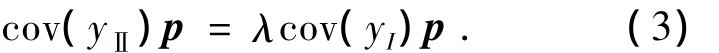
式中:λ为广义特征值;p为对应的特征向量.其矩阵形式为

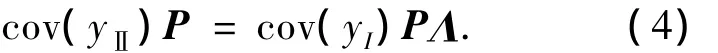
式中:P= ［p1，p2，…pq］，Λ =diag(λ1，λ2，…λq).最大的广义特征值λmax所对应的特征向量pmax为控制性能变得最差所投影的方向.求上式的行列式得

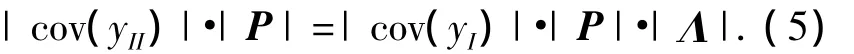
从而得到表征总体性能的指标IV如下:

由性能指标(6)可知:IV＞1时，监控的控制器性能比历史基准性能要差;IV＜1时，监控的控制器性能比历史基准性能要好;IV≈1时，监控的控制器性能与历史基准性能较为接近，较小的偏差可认为是统计误差.只有明显偏离1时，才认为性能发生较为显著的变化.

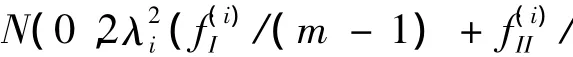
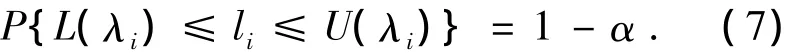
对应于

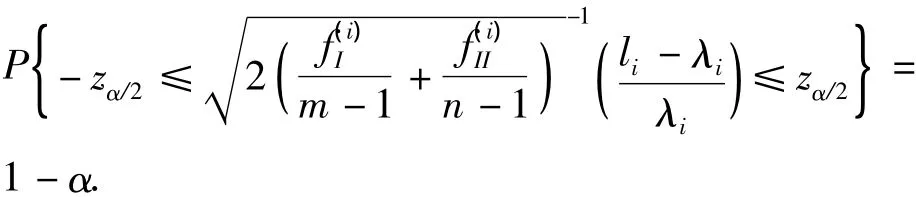
由此可得li的置信上限U(λi)和置信下限L(λi)

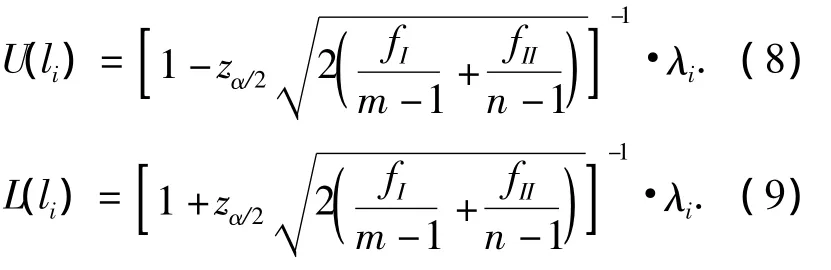
当L(λi)＞1，可以判断总体特征值的真值大于l，表明监控的控制器性能差于沿此特征值对应的特征向量方向上的基准性能;当U(λi)＜1，可以判断总体特征值的真值小于1，表明监控的控制器性能优于沿此特征值对应的特征向量方向上的基准性能;当L(λi)＜1＜U(λi)，从统计角度可判断总体特征值真值等于1，表明监控性能沿此特征值对应的特征向量方向上与基准性能差别不大.

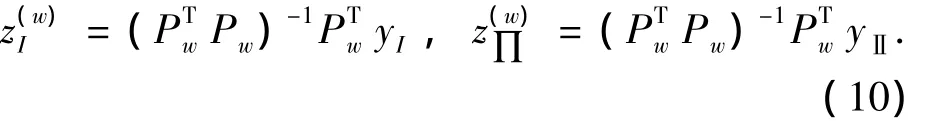
同时可获得基于协方差数据驱动的恶化性能子空间的评估指标Iw

指标Iw给出了所监控的数据与历史基准数据在恶化性能子空间中投影方差的比值，其可作为沿恶化特征方向的控制器性能下降程度的度量指标来判断控制器的性能好坏.

2 正确选择性能基准数据的必要性

文献［5］等所给方法可直观有效地对控制器进行性能评估，但其只考虑评估基准是单一工况的情况，未考虑在多工况下评估基准的选择问题.由于评估基准选择的不当有可能带来的对控制器性能评估的误判，如无法判断是控制器性能的真实下降还是由于基准选择不当造成的性能下降的结果而得出错误的结论.以下这个2输入2输出的例子可以说明未考虑多工况评估基准而得到错误评估结果的问题.

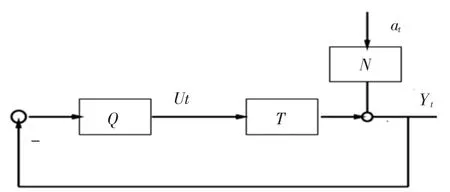
图1 多变量反馈控制系统示意图

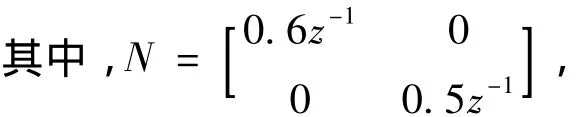
白噪声协方差阵

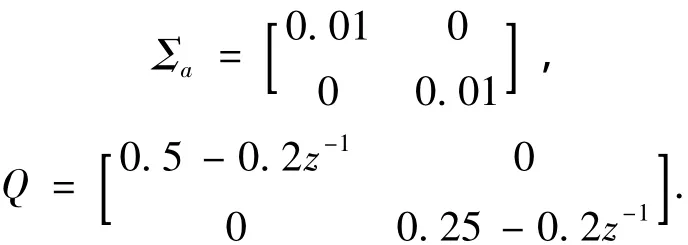
考虑两种工况:

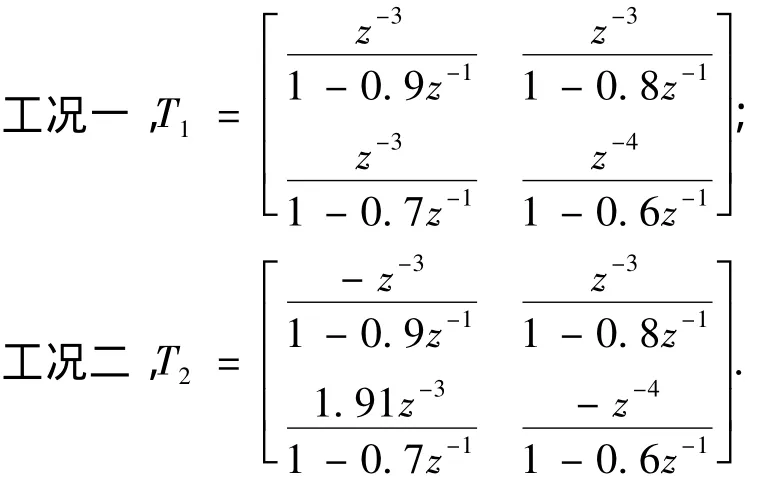
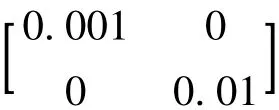
故应采用工况二的数据作为评估基准才能得出正确的评估结果，倘若随意选择评估基准，则会得到与事实相反的评估结果，造成误判.

从该例不难说明，在用基于数据驱动的方法进行性能评估时，控制器性能基准的选取是十分重要的，若控制性能基准选取不当，将会在很大程度上影响评估结果的准确性.

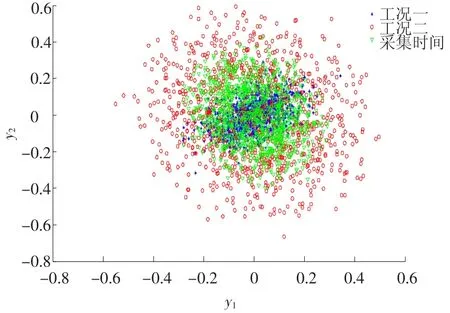
图2 多变量系统输出变量三组数据二维联合分布

3 基于综合相似因子SF的多工况性能评估

上文已阐述了选择性能评估基准的必要性与重要性，针对多变量多工况的条件下，本文提出一种基于综合相似因子距离度量的方法，在进行评估之前，先对所采集的数据与历史数据库中各类工况下的基准数据分别进行匹配，找出所采集数据所属的工况，再进行性能评估，这样方能保证评估结果的正确.

3.1 PCA相似因子

文献［9－10］给出了一种基于PCA相似因子的方法来衡量两类数据矩阵之间的相似性.假设历史数据阵H和实时数据阵S，均有n个变量(数据矩阵列数为n)，它们各自的PCA模型中均包含有k个主元，k≤n，k按如下原则选取:k个主元的方差之和占到总方差的95%以上，则H与S相对应的主元子空间分别为L和M，根据文献［9－10］，PCA相似因子按如下公式计算:

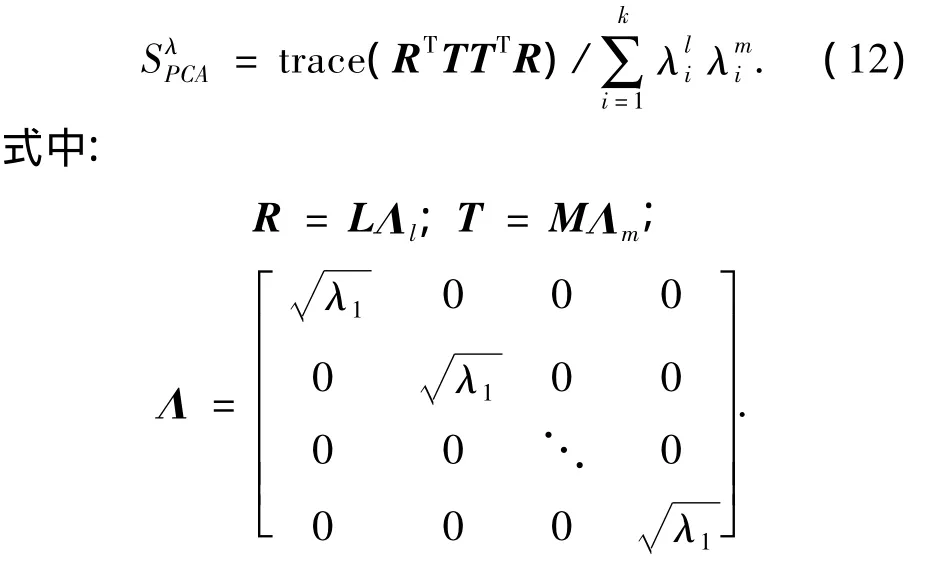
通过式(12)得到的PCA相似因子可以衡量两数据矩阵的相似程度，从几何意义上说，SλPCA表征的是两组数据矩阵在空间中分布形状的相似程度，却未考虑两组数据之间的几何距离因素，因此还需引入表征几何距离的度量因子才能得到更加准确的分类结果.

3.2 几何距离相似因子

若两组数据矩阵在空间分布上具有类似的几何形状，却相互隔着一定的空间距离，此时PCA相似因子对区分两组数据矩阵几乎不起什么作用，引入几何距离相似因子可以将该条件下的数据阵区分开来.

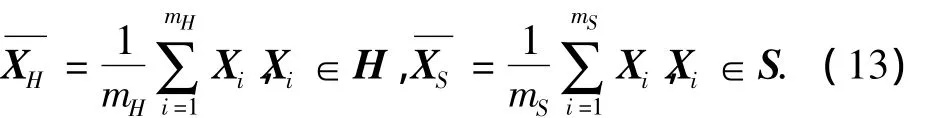
mH和mS分别为数据阵H和S的采样数，Xi为数据阵的第i次采样值.两组中心向量之间的马氏距离定义为

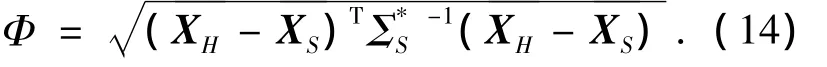
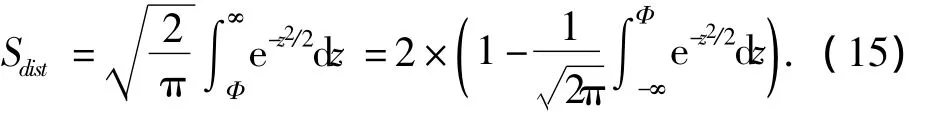
几何距离因子很好地补充了单用PCA因子来衡量两类数据相似性的不足之处.

3.3 综合相似因子SF

在实际应用中，必须综合考虑这两类度量因子的因素，一种简单而有效的方法是将两类因子进行加权组合构成综合相似因子

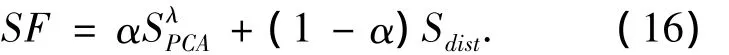
其中:0≤α≤1，若无任何先验知识的情况下，α可取0.5.实际应用中的具体步骤如下:计算实时采集的数据阵与历史数据库中的每一类工况下的数据阵的SF值，选取SF最大值所对应的那一类工况作为实时采集数据所属的工况，而后再按照基于数据驱动的方法进行性能评估.

3.4 多工况基准数据的性能评估

针对历史数据库中有多种工况下的历史数据，将实时采集的数据阵与历史数据库中的每一类工况的基准数据一一比对，找出相似程度最高的那一类工况，从而将该实时采集的数据判定为那一类工况，而后再进行性能评估.

综上所述，多工况过程基准数据的性能评估过程为

1)收集所有可能工况的历史基准数据集.

3)根据已有的先验知识，选择一定的权重α，计算SF综合相似因子.

4)选取SF最大值所对应的那一类工况作为实时采集数据所属的工况.

5)将实时采集数据与其所属工况的历史基准数据进行基于数据驱动型的性能评估.

4 仿真分析

4.1 文中第三部分的仿真例子

第三部分所给的例子三组输出数据如图3所示.将SF综合相似因子应用到第三部分所给的例子中，将实时采集的数据分别与工况一(I)和工况二(II)下的数据用SF综合相似因子进行衡量，得到表1.由表中结果可以看出，实时采集的数据与工况二下的数据SF因子最大，故实时数据应被归类与工况二下的数据，应选取历史数据库中工况二下的数据作为性能评估基准，再进行性能评估.该例子证实了用SF综合相似因子来衡量数据矩阵之间相似程度的有效性.

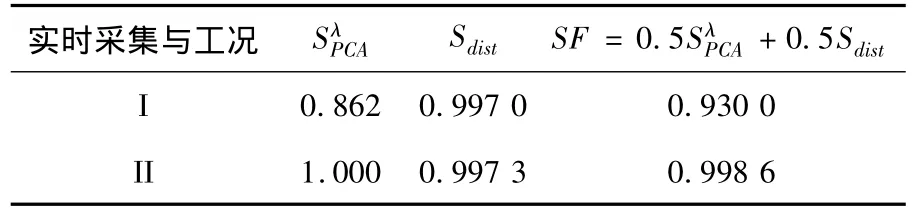
表1 采集数据阵与两类工况下数据阵的相似性比较

4.2 一个4输入4输出的仿真例子

由McNabb和Qin［11］提供的4输入4输出的仿真例子如下:

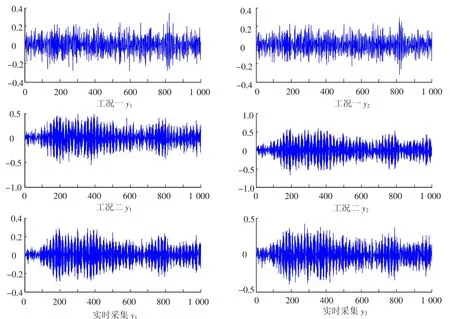
图3 实时采集的数据与不同工况基准的数据

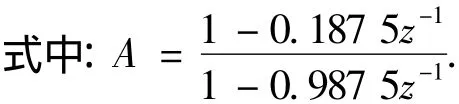
其中白噪声协方差阵

考虑两种工况:

工况一，

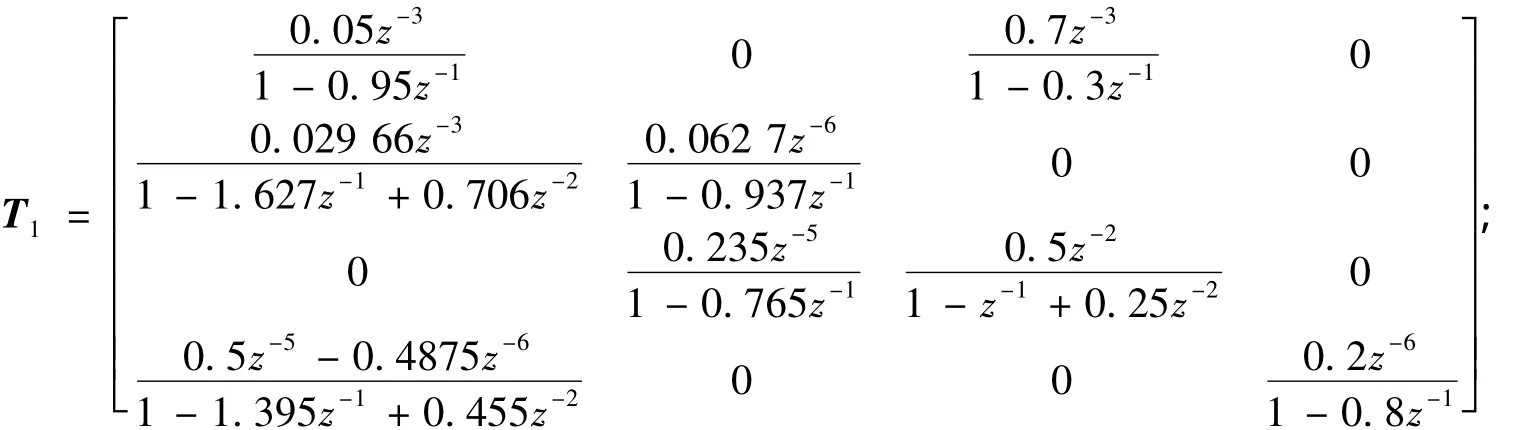
工况二，

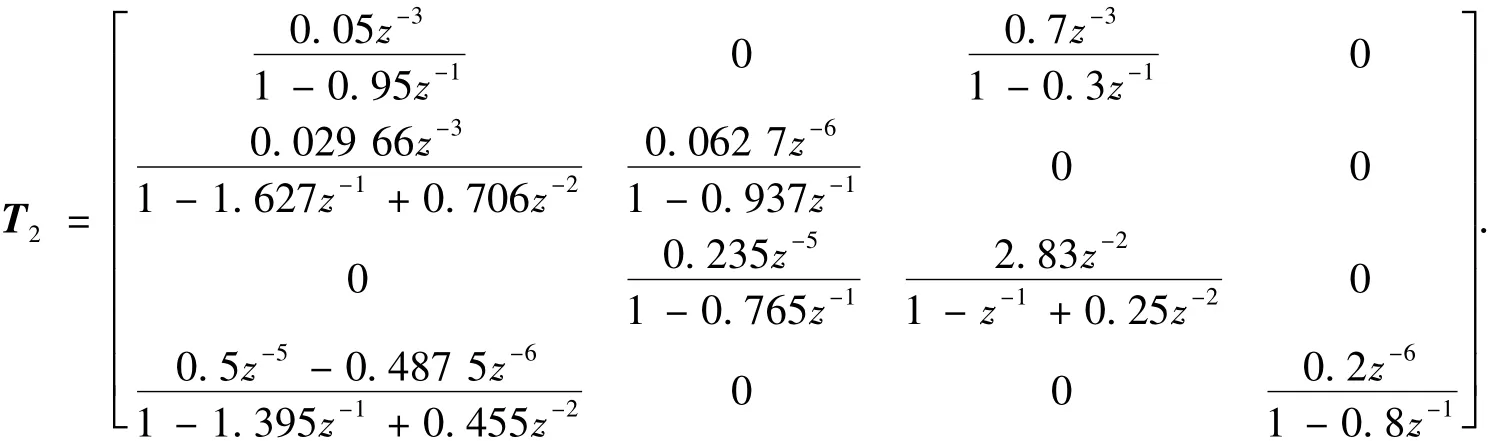
由评估结果分析可知:若选取工况一的数据作评估基准，则实时采集的数据整体性能上是显著变差的;若选取工况二的数据作评估基准，则在整体性能上是得到改进的.而实际采集的数据是来自工况一的，由于白噪声的方差变大，控制性能恶化是符合事实的.

采用本文的提出的SF综合相似因子对所采集的数据进行归类，将实时采集的数据分别与工况一(I)和工况二(II)下的数据用SF综合相似因子进行衡量，得到2表.

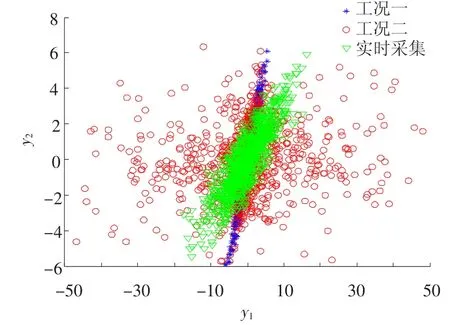
图4 文献［11］例子回路一与回路二输出变量三组数据二维联合分布图

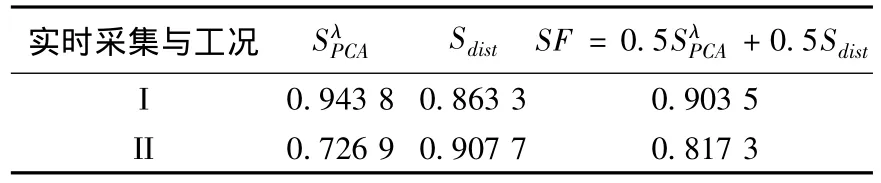
表2 文献［11］例子中采集数据阵与两类工况下数据阵的相似性比较

由表中结果可以看出，实时采集的数据与工况二下的数据SF因子最大，故实时数据应被归类与工况二下的数据，应选取历史数据库中工况二下的数据作为性能评估基准，再进行性能评估，这样方能得到正确的性能评估的结果.

5 结论

本文提出一种针对多变量多工况条件下基于数据驱动的性能评估的方法，用仿真例子阐述了在进行性能评估前选取历史数据库中恰当的基准数据的重要性和必要性，采用综合PCA相似因子与几何距离因子的SF综合相似因子对所采集的数据与历史库中各工况下的数据进行正确的归类，从而才能保证性能评估结果的正确性，仿真例子证实了该方法的有效性.

［1］DUGARD L，GOODWIN G C，XIANYA X.The role of the interactor matrix in multivariable stochastic adaptive control［J］.Automatica，1984，20(5):701 －709.

［2］HARRIS T J，BOUDREAU F，MACGREGOR J F.Performance assessment of multivariable feedback controllers［J］.Automatica，1996，32(11):1505 －1518.

［3］HUANG B，SHAH S L，KWOK E K.Good，bad or optimal?Performance assessment of multivariable processes［J］.Automatica，1997，33(6):1175 －1183.

［4］QIN S J，YU J.Recent developments in multivariable controller performancemonitoring ［J］. Journalof Process Control，2007，17(3):221 －227.

［5］YU H，QIN S J.Statistical MIMO controller performance monitoring.Part I:Data-driven covariance benchmark［J］.Journal of Process Control，2008，18(3 －4):277－296.

［6］YU H，QIN S J.Statistical MIMO controller performance monitoring.Part II:Performance diagnosis［J］.Journal of Process Control，2008，18(3－4):297－319.

［7］TIAN X M，CHEN G Q，CHEN S.A data-based approach for multivariate model predictive control performance monitoring［J］.Neurocomputing，2011.74(4):588 －597.

［8］PUSHA S，GUDI R，NORONHA S.Polar classification with correspondence analysis for fault isolation［J］.Journal of Process Control，2009，19(4):656 －663.

［9］SINGHAL A，SEBORG D E.Pattern matching in historical batch data using PCA［J］.IEEE Control Systems Magazine，2002，22(5):53－63.

［10］SINGHAL A，SEBORG D E.Pattern matching in multivariate time series databases using a moving-window approach［J］.Industrial ＆ Engineering Chemistry Research，2002，41(16):3822－3838.

［11］McNabb C A，Qin S J.Fault diagnosis in the feedbackinvariant subspace of closed-loop systems［J］.Industrial＆ Engineering Chemistry Research，2005，44(8):2359－2368.

The performance assessment of multiple mode MIMO industrial process based on Data-driven controller

LIN Xiao-zhong，XIE Lei

(Institute of Cyber-Systems＆ Control，State Key Laboratory of Industrial Control Technology，Zhejiang University，310027 Hangzhou，China)

To choose the suitable benchmark data for data-driven controller performance monitoring from data based on kinds of multiple mode in the history database，a new method based on multiple variables classification is proposed.First the method provides a combined similarity factor to measure the similarity between realtime acquisition data and data from some mode in the history database，and then it determines the mode that real-time data belongs to，finally it assesses the controller performance.Simulation study demonstrates the efficiency of the proposed approach.

multiple mode，similarity factor，performance assessment

林晓钟，shangdonghappy@126.com.MIMO线性反馈控制系统的性能评价，并对控制变量协方差矩阵的理论下界评价进行了定量分析.Huang［3］研究了MIMO前馈反馈控制器的性能评价，通过对操作数据处理得到前馈反馈最小方差从而作为性能监视的基准.大多数基于MVC基准和LQG基准的性能评估方法离不开过程的传递函数模型，而实际过程中过程的模型又不容易精确地获得，使得这些方法的应用受到了限制.

TP14

A

0367－6234(2012)11－0081－06

随着现代工业及科学技术的迅速发展，现代化的流程工业呈现出规模大、结构复杂、生产单元之间强耦合等特点.在复杂工业过程中，控制回路数目众多，这些控制回路大多在运行初期具有良好的性能，在运行一段时间后，受原料性质、对象特征、优化目标变化以及维护不利等各种因素的影响，控制回路性能将会变差，导致产品的质量和工厂的效益受到影响，所以工业界对控制系统性能要求的提高促进了控制系统性能评估这一领域的发展.最初，很多研究主要聚焦在基于最小方差基准(MVC)的 SISO 系统的性能监视方面［1－2］研究了

2012－02－13.

国家自然科学基金资助项目(61134007).

林晓钟(1986—)男，硕士研究生;

谢 磊(1979—)男，副教授，博士生导师.

(编辑 苗秀芝)