改进层析算法在混凝土超声成像中的应用

李秋锋，马辉聪，陈文生，廖 寅

(无损检测技术教育部重点实验室(南昌航空大学)，南昌330063)

0 引言

计算机层析成像是计算机科学、放射学等结合在一起而产生的一门新的成像技术，是一种先进的可视化技术［1］。它是在无损状态下获得被检物体断面的二维图像，然后以图像形式直观、准确、清晰地展现被检物体内部的结构特征。

射线追踪理论依据是高频近似条件下波场能量沿轨迹传播［2-3］。混凝土超声CT中，以往使用的是直线追踪方法，该方法认为射线在介质中直线传播，而超声波在不均匀的介质传播的路径由于折射、散射而弯曲，使得采用直线追踪法追踪超声传播路径失效;因此，有必要在超声CT中引入曲线追踪方法。曲线追踪的方法很多［4］，其中，基于SNELL定律的射线追踪方法是基于Huygens原理一种局部走时算法，该法简单直观，且在实际应用中，求共发射、共接收点或多发射点等情况下的射线路径时可以提高计算速度［5］。经典的反演算法，如ART和SIRT，都是在局部连续寻优，对于多极值型的目标反演函数，结果可能得到的只是局部解，往往导致结果不准确甚至失效。模拟退火算法对求解方程没有连续性、可导性等数学要求，对于多极值问题能够全局寻优。本研究把混沌搜索和自然权函数引入模拟退火算法中，通过混沌搜索实现在解空间中离散均匀产生解向量，而自然权函数充分考虑了超声在混凝土中的传播特点，在模拟退火算法中约束解空间范围。自然权函数和混沌搜索的引入能提高反演求解准确度。

1 CT基本原理

为说明CT原理，建立J=r×l个网格的模型，从发射探头T到接收探头R的第i条射线路径传播路径距离为Li，模型见图1。由Radon公式可得从激发点到接收点的实测走时［6］式中:x，y表示单元位置;Vj(x，y)为第j个成像单元的超声波速;fj(x，y)为第j个成像单元的波慢(即波速的倒数)。

图1 超声测试原理图Fig.1 Ultrasonic test theory

若成像单元足够的小，则可将每个单元fj(x，y)视为常数，则式(1)可写成级数形式并用矩阵方程表示为

式中:A中元素aij为第i条射线在第j个成像单元内的线段长，走时向量图像灰度向量。

2 弯曲射线追踪原理

弯曲射线追踪算法适用于速度分布模型，由2个部分组成，首先初选射线路径，然后对路径扰动以确定超声传播路径。扰动方法依据任意2种介质的分界面两侧射线路径应符合SNELL折射定律［7］。

2.1 对于任意速度界面修正

为推导任意界面两侧超声传播路径修正量，建立推导模型(图2)。在分界面两侧的A、B、C三点，A点处介质速度为v1，C点处介质速度为v2，B位于分界面上，顺序连接 A、B、C点，然后根据Fermat定律对B点修正，使从A点经过修正点B'再到C点的走时最小，将从出发点到接收点的所有路径修正点连接起来，当校正量范数满足一定精度要求时，即构成整条射线路径［8］。

图2 任意界面射线传播修正图Fig.2 Ray propagation modification of arbitrary

图2中，假设z=f(x)为介质分界面函数，A(x3，z3)和 C(x1，z1)为介质两边端点，B(x2，f(x2))为界面的初始点，B'(x2+Δx，f(x2+Δx))为校正后的点，根据费马原理和Taylor展开并取1阶最小量，得校正量

2.2 对于水平(垂直)层状界面

根据上述任意速度分界面超声传播路径修正公式的结论，对于水平分界面的情况，建立如图3所示的修正模型，f'=0，f″=0假设分界面函数为z=z2，则式(3)可简化为

图3 水平界面射线传播修正Fig.3 Ray propagation modification of horizontal interface

对于矩形网格，超声传播路径与网格水平，垂直方向相交，采用式(4)对试射路径修正，由于式(4)隐含射线在一个网格内修正［9］，若修正点超过一个网格，则用网格纵横交叉点代替修正点。

3 改进模拟退火算法

模拟退火算法求解组合优化问题，首先给问题一个初始解和初始温度，根据给定初始解计算目标函数，然后对初始解扰动产生新解和新的目标函数解，采用一定的规则接收新解，通常依据Metropolis准则接收新解，其接受概率［10］

生成函数通常用于产生扰动新解，高斯函数GG≈exp［－m2/T(t)］为常用生成函数。其中，m为解空间中的任意初始值，T为温度。这种生成函数降温速度慢，容易陷入局部搜索，本文将混沌搜索引入模拟退火算法，将模拟退火算法的全局搜索性和混沌搜索的解空间均匀遍历性结合起来，提高算法计算精度。

由于式(2)求解的欠定性和方程组不相容等特点，为求满意解，总是要采用某种最优化准则，根据最小距离准则和超声传播的先验约束准则构造自然权函数［11］

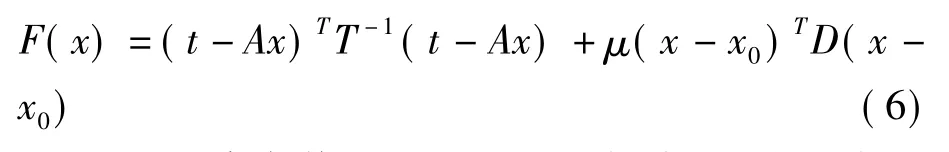
式中:x为待求值，T、D均为对角阵，D中对角元素值为超声穿越单元长度与其单元速度乘积，T中对角元素值为超声传播各路径走时。为超声路径穿越任一单元的长度和与相应单元速度乘积。该自然权函数的特点是，对长度小的路径加重权，增大短距离路径信息的有效性比重，对同一像素而言，超声波路径穿越的次数越多，信息量越大，加重权可以增大超声路径穿越多的像素的信息有效性。

混沌搜索是混沌动力学模型里的一种基于Logistic映射的简单非线性映射模型［12-13］。

其中，μ为控制参数，n∈［0，1］。当 μ=4时，Logistic映射在区间［0，1］上均匀分布，引入混沌搜索，使得模拟退火算法在初始温度下具有较好的随机性，并可以在解空间全局搜索最优解。同时，由于反演区域网格数比较大，自然权函数存在大量极小值，故在每轮降温后再加入回火环节，在每次回火过程中，根据超声传播特点构造的自然权函数，可以起到约束解空间，改善求解方程欠定性和不相容性的作用，具体算法反演流程如图4所示。回火结束，输出最优解，输出速度分布图，反演结束。

4 数值仿真实验

算例的速度模型如图5所示。测区面积为1200 mm ×1200 mm，像元为200 mm ×200 mm，混凝土区域波速为4396 m/s(根据模型参数计算)，模型中心有个缺陷区，波速为3 177 m/s。材料参数如表1所示，测区速度由材料参数并和式(8)计算得到。

根据模型波速和曲线射线追踪得出射线路径和每条射线行走时间，并将此走时时间作为理论时间，采用模拟退火算法和改进模拟退火算法得到的反演结果分别如图6和图7所示，其等值图分别如图8和图9所示。

图4 改进模拟退火算法流程图Fig.4 Flowchart of improved SA algorithm

图5 模拟计算模型Fig.5 Simulation computation model

综合比较图6与图7、图8与图9的模型反演结果可以看出，在数据量有限的情况下，成像效果能够满足要求。单从反演结果来看，2种模拟退火算法程序都能较有效地反映混凝土内部的缺陷，在取得数据数量有限的情况下，图像反演的质量也较高，具有一定的精度。虽然图中都可以反映出缺陷位置，但是图6b显示模型在缺陷区波速平均值为3750.9 m/s，与设定的理论值相差较大，如果嵌入目标与混凝土声速相差不大，很难区分开，容易造成结果失效;而图7b中模型缺陷区平均波速为3175.7 m/s，计算结果更接近模型的理论速度，说明改进模拟退火算法计算更准确，更符合实际，而且在非缺陷区波速过渡快，具有更高的分辨率。

图6 模拟退火算法反演像素与速度对照图Fig.6 Inversion pixel image contrast to velocity value by SA algorithm

图7 改进模拟退火算法反演像素与速度对照图Fig.7 Inversion pixel image contrast to velocity value by improved SA algorithm

表1 模型参数Table 1 Model parameter

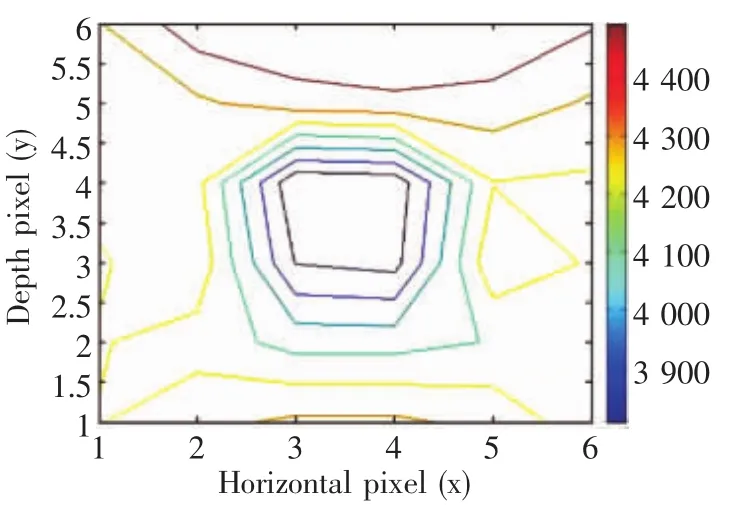
图8 模拟退火算法反演等值图Fig.8 Inversion same value image by SA algorithm

图9 改进模拟退火算法反演等值图Fig.9 Inversion same value image by improved SA algorithm

5 结论

1)改进层析算法可提高反演分辨率，求解精度高;

2)基于SNELL定律和Fermat原理的射线追踪方法非常适用于混凝土超声检测;

3)在反演中引入自然权函数，在每轮回火重新构造自然权函数，可以缩小解空间;

4)根据混沌追踪的离散特点可以得到具有全局性的求解，避免陷入求解局部最优解;

5)改进算法在数据量不多的情况下也能得比较好的成像结果，适用于混凝土超声成像。

［1］Feschet F，Gerard Y.Computerized tomography with digital lines and linear programming［A］，Proceedings of the 12th International Conference on Discrete Geometry for Computer Imagery［C］//Heidelberg，Germany:Springer Verlag，2005，3429:126 －135.

［2］Grunberg M，Genaud S.Mongenet Catherine Seismicray-tracing and Earth mesh modeling on various parallel architectures［J］.Journal of supercomputing，2004，29(1):27－44.

［3］张钋，刘洪，李幼铭，等.射线追踪方法的发展现状［J］.地球物理学进展，2000，15(1):36－45.

［4］Wang H Q.Improvement and realization of linear travel-time interpolation ray tracing algorithm［J］.Russian Journal of Nondestructive Testing，2010，46(9):690 －697.

［5］赵忠伟，骆英，李忠芳，等.混凝土射线追踪方及其模拟计算［J］.公路交通科技，2008，25(8):73－74.

［6］王五平，宋人心，傅翔，等.用超声波CT探测混凝土内部缺陷［J］.水利水运工程学报，2003，(2):57－58.

［7］唐修生，王五平，方璟，等.基于Snell定律的射线追踪程序实现及模拟计算［J］.焦作工学院学报，2004，23(2):119－120.

［8］卫山.二维复杂介质的建模及逐段迭代射线追踪方法的应用研究［D］.武汉:中国科学技术大学，2001，23(6):72－76.

［9］张建中，陈世军，余大祥，等.最短路径射线追踪方法实现及其改进［J］.地球物理学进展，2003，18(1):146－150.

［10］Kirkpatrick S，Gelatt C D，Vecchi M P.Optimization by simulated Annealing［J］.Science，1983，220(4598):671 － 680.

［11］Berryman J G.Fermat’s principle and nonlinear travel time tomography［J］.Physical Review Letter，1989，62(25):2953 －2956.

［12］方振国，陈得宝.新的基于混沌搜索的组合优化算法［J］.计算机应用，2011，3(3):658－659.

［13］Zhang H J.Hu Y F.A hybrid chaotic quantum evolutionary algorithm for resource combinatorial optimization in manufacturing grid system［J］.International Journal of Advanced Manufacturing Technology，2011，52(5－8):821－831.