直升机动力传动系统故障诊断方法
徐英帅,王细洋,孙 伟,胡贵锋
(南昌航空大学航空制造工程学院,南昌330063)
0 引言
动力传动系统是直升机中最主要的机械系统,它直接决定直升机的机动性能、飞行寿命以及飞行安全性,它很容易发生故障,并且发生故障往往都会引起很严重的后果。当今世界上绝大多数直升机为单旋翼带尾桨式,这种形式的直升机传动系统通常包括3个减速器——主、中、尾减速器[1]。其中主减速器在直升机传动系统中的作用至为关键。主减速器主要由齿轮传动机构以及机匣组成,与发动机一起安装于传动系统整流罩内。主减速器的基本功能之一是降低发动机转速和改变传动角度。转速降低,则输出轴扭矩就会增大。传动系统降速比要求非常大,因而均采用行星轮系进行降速[2-3]。
行星齿轮传动系是直升机动力传动系统的关键部分,动力系统事故多出于行星传动系。在大功率、高转速、高负载的工作环境下,行星齿轮系极容易发生齿面磨损、齿面接触疲劳、轮齿弯曲疲劳乃至断齿或轴断裂等失效现象,大幅度缩短了直升机动力传动系统的寿命,影响飞行安全性,甚至导致飞行故障[4-6]。实际上,行星齿轮故障诊断的研究也主要出自直升机动力系统可靠性方面的需求,其研究成果逐渐应用于其他采用行星齿轮系的机械。我国空军部门的飞行实践和直升机企业的维修经验也证实,行星齿轮系的故障是直升机动力传动系统产生故障的主要原因。为此研制的行星齿轮箱故障诊断试验台、检测分析系统,将可作为直升机的机载设备之一,在飞行中予以及时的警示。
1 齿轮振动与信号分离方法
1.1 行星齿轮振动分析
齿轮可看做是由轮齿和轮体组成的振动系统。在润滑良好且齿面摩擦度低的情况下,齿面上摩擦力的作用常可忽略,此时齿轮副的振动方程[7]可以表示为
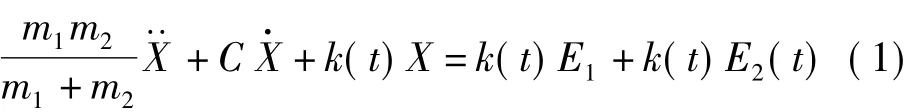
式中,X是沿啮合线上齿轮的相对位移,k(t)是齿轮啮合刚度,m1和m2分别是齿轮副中主动轮与从动轮的质量,C是齿轮啮合阻尼系数,E1是齿轮受载后的平均静弹性变形,E2(t)是齿轮故障函数。等式的前端代表齿轮副本身的振动特征,后端代表激振函数。
由于激振函数中k(t)是周期性的变量,因此齿轮在无故障的理想情况下也存在振动,这样的振动称为啮合振动。该振动是以每齿啮合为基本频率的,即啮合频率,行星齿轮啮合频率的计算式[8]可以表示为

其中,fc、fp、fs分别是行星架、行星轮和太阳轮的旋转频率,Nr、Np、Ns分别是齿圈、行星轮和太阳轮的轮齿个数。激振函数中k(t)E2(t)是激励源,可导致齿轮振动异常。检测出由故障激励源所造成的异常振动的特征是诊断齿轮故障的主要任务。一般情况下,齿轮产生故障失效之后,振动信号的特征当中会产生幅值调制与相位调制,故齿轮振动信号的数学模型可以表示为

其中,rk(t)和φk(t)分别是调幅信号与调相信号。对于没有任何缺陷的齿轮,也不会有调制现象;当齿轮出现异常时,就会出现调制现象,并且随着缺陷的加剧,调制也会越深。
理想的行星轮振动信号通过安装在行星齿轮传动机构齿圈上的传感器获得,是单个行星齿轮振动的总和,在行星轮转动通过传感器位置时会产生多次调制现象,即行星通过调制。理想的行星轮振动信号表达式如下:

其中,αp(t)是行星轮p的幅值调制函数,υp(t)是行星轮p的轮齿啮合振动函数,p相当于单个的齿轮,P是行星轮的个数。所有行星轮的幅值调制函数αp(t)有相同的形式,不同的仅仅是延迟时间,行星架重复旋转时间为1/fc,则有

其中,a(t)是行星通过调制函数,A(m)是它的傅里叶变换。
1.2 行星齿轮信号分离方法
对指定齿轮箱旋转振动信号进行同步采样,如果能保证不同时刻采集信号的起始点相位一致,并保证采样频率与采集的点数一样,这样的时域信号不但可以平均,而且还可大大提高指定周期信号的信噪比,并能减少或抑制不相干的振动信号成分,进而只提取相关的振动信息,这种方法称为时域同步平均[7-9]。概括的讲就是从齿轮振动中取出啮合频率成分,并将它与齿轮轴的旋转频率同步相加、平均,是从混杂有噪声干扰的信号中提取周期性分量的有效方法。
时域同步平均展示了齿轮箱旋转超过1转时齿轮啮合振动的形式,包括一些调制的影响,同时它的频谱还包含相关齿轮啮合成分与边频带簇。因此,时域同步平均[10]可以表示为
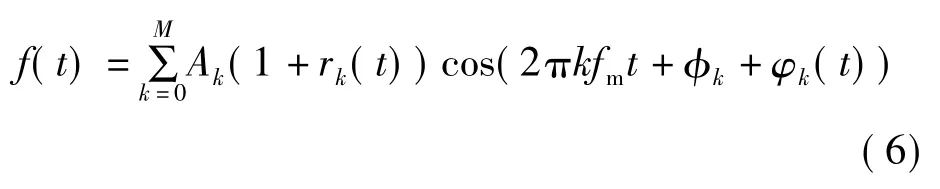
式中,Ak与φk分别为k阶啮合谐波频率的振幅与相位,fm为齿轮的啮合频率,M为齿轮啮合谐波频率的阶数。相同谐波频率调制的影响包括振幅调制和相位调制,其中1+rk(t)为振幅调制函数,φk(t)为相位调制函数,伴随着齿轮的旋转频率这些调制函数是呈周期性的。时域同步平均法在齿轮故障的转动频率与出现频率同步时,才会起到增强故障信号的作用。齿轮的轮齿破损和轴破损都属于这类信号,故时域同步平均法对齿轮故障诊断十分有效。随着平均次数的逐渐增加,齿轮旋转频率与啮合频率及其各阶倍频成分被保留,而其他轴的振动信号和噪声部分相互抵消趋于消失,由此便可得到仅与被检测齿轮振动有关的信号。
提取每个行星轮典型的信号平均的方法包含了将连续时间信号过滤成平均信号的过程。时间滤波器能够把整周期的振动信号分解成每个行星轮的振动信号。每个行星轮的信号平均的时间窗b(t)加在行星轮靠近传感器的振动点上。相关行星轮经过滤波的振动信号的信号平均有相等的周期1/(fp+fc),当时间滤波信号平均 zp(t)超过周期为1/(fp+fc)的iNr时,

分离函数c(n)通过外加时间窗b(t)和行星通过调制函数a(t)来定义。

分离窗是一个余弦窗,表达式如下:

该函数是一个递减函数,当行星轮接近传感器时取最大值,当行星轮离传感器最远时取0值。
2 试验设计
该故障诊断方法的主要步骤包括:将振动传感器放置在与内齿圈相连的位置;齿轮传动机构在运行时会产生振动,通过传感器获得一个完整的振动信号;逐个的分离来自于每个行星齿轮的振动信号。
试验框图如图1所示。齿轮箱由交流电动机驱动,齿轮传动扭矩的变化由控制电动机输出电流的数字式矢量驱动单元来实现。3个加速度计式振动传感器安装在齿轮箱基座上,同时在扭矩测量单元上安装扭矩传感器,在电动机与齿轮箱之间安装编码器以获得转速同步脉冲信号,用于转速测量及时域同步平均。传感器的采集信息通过数据采集卡输入计算机。采用基于LABVIEW的虚拟仪器技术进行数据采集。

图1 齿轮传动故障诊断试验系统框图Fig.1 Block diagram of fault diagnosis system for gear transmission
行星齿轮箱故障诊断试验台如图2所示。行星齿轮箱采用内外中心轮结构,使用精密行星减速机,型号为PXDS115-50(上海磊诺)。该行星齿轮箱为二级行星齿轮变速箱,有输入级和输出级2部分:输入级有3个行星轮,1个太阳轮和1个内齿圈,每个行星轮有36个齿,太阳轮有12个齿,内齿圈有84个齿;输出级也有3个行星轮,1个太阳轮和1个内齿圈,每个行星轮有28个齿,太阳轮有14个齿,内齿圈有70个齿。齿轮箱由型号为Y100L2-4的三相异步电动机驱动,该电动机的同步转速为1.43 kr/min,额定功率为3.0 kW,在该电机的匀速驱动下通过刚性联轴器传递给光电编码器,最后把动力传递给行星齿轮减速箱。在行星齿轮箱输入级内齿圈的外围布置了3个振动传感器,型号为CA-YD-1182(江苏联能),是内装IC放大器的ICP型压电加速度计式振动传感器,传感器以磁吸式安装在齿轮箱体上,这3个传感器对行星齿轮箱内部的3个行星齿轮进行振动信号测量。测量得到信号经过功率放大器后,在恒流源、研华多功能 USB模块 USB-4711A数据采集卡的共同作用下,将所需要的信号进行有效地放大保存。

图2 行星齿轮箱故障诊断试验台Fig.2 Fault diagnosis test-bed for planet gearbox
利用LABVIEW虚拟仪器平台建立数据采集系统。该系统可以进行多通道同时采集信号,正适合该试验所设计的多传感器采集信号的形式;并可实时显示任意通道的时域信息,有助于在线预测估计齿轮的故障信息;同时,系统可以选择采集卡类型,设置通道数目、文件个数等,方便试验的进行。在本试验中,设置通道数目为3,采样频率为60 kHz,采样点数为61 440,采集的信号经A/D转换器转换成数字信号后,再按一定格式转换成数据文件存储到硬盘里。
为了便于试验将输入级的3个行星轮进行编号,如图3a所示。行星齿轮箱是在空载的情况下运行的,为了得到行星齿轮损坏后的信号,故人为使齿轮毁坏失效,将故障嵌入到输入级的1个行星轮上,用锉刀使行星轮2的轮齿有一定程度的破损,如图3b所示。然后对行星齿轮箱进行齿轮啮合试验,并记录行星齿轮箱的振动信号。

图3 行星齿轮啮合试验Fig.3 Meshing experiment of planet gears
3 试验结果
假设行星齿轮箱的速度是不变的,实际上,即使名义上的不变速机械这种情况也不是永恒的。要允许速度的波动所有分析是在角域下被执行的;这仅仅涉及一个角度,与时间变量t无关。从时域到角域的转化要通过对振动信号的同步,采集一个齿轮箱的角度信号,这个同步也能使用锁相频率系数或数字式的重复采样。
为了计算时间窗信号平均行星架的参考位置,要求设置在开始时间(t=0)的那个点上,即传感器与其中的一个行星轮(p=P)接近的位置。这个参考位置可以通过放置在行星架上的轴编码器转速计来获得(通常是齿轮箱的输出),或通过软件同步行星通过调制信号。这需要执行行星架(内齿圈)振动信号平均。每个行星轮通过传感器位置时振动水平增加,会产生一个振动信号的幅值调制。内齿圈关于齿轮啮合振动信号平均的解调被用来决定调制峰值,作为每个行星齿轮通过传感器的位置。在解调信号平均当中最大幅值点被选择作为行星架参考位置的零点。
图4所示是旋转函数的信号幅值图,是通过执行窄带包络线增强获得的结果。分离故障行星轮的信号平均使用式(9)所定义的带有时间窗的行星齿轮信号分离方法,分析时间只有75 s(10×36行星架的旋转)。窄带包络线的峭度(峰值)被用来作为齿轮局部振动啮合行为的标准。峭度值大于4.5表明存在明显的局部故障,该值低于3.5表明是一个完好的齿轮。这里给出一个7.2的峭度,明确的指出故障的存在。

图4 旋转函数的信号幅值图Fig.4 Signal amplitude value as a function of rotation
图5所示是行齿轮信号分离方法的性能分析,数据长度的改变作为行星齿轮故障检测的标准。将图中3个行星轮的峭度、平均次数相比来进行分析;图中也包括了警告(峭度=3.5)和危险(峭度=4.5)的参考水平。每次平均代表行星架的36个旋转(相关行星齿轮旋转的84个周期),在这种情况下,大约需要7.5 s的数据。现将这些数据和行星架的参考位置应用到这种方法当中。
可以看到图5所示的行星齿轮信号分离方法非常有效和稳定:仅一次平均之后,一个非常明显的故障指示在行星轮2中产生,而且伴随相关好的分离(行星轮3低于警告水平线);仅3次平均之后,就完成了极好的故障检测和行星分离(在未损坏的齿轮上不会出现有故障的证据);10次平均之后,新的行星分离已完全稳定,并且通过进一步的平均有非常小的改变。

图5 平均次数函数的齿轮峭度值Fig.5 Gear kurtosis value as a function of number of averaging
4 结论
1)通过对单个行星齿轮振动信号进行适当的分离,可以实现在信号平均时不丢失信息,而且不再履行传统信号平均的那些要求。这种方法可以分离出每个行星轮的振动信号,给出每个行星轮的分离信号平均,进而估计每个行星轮对全部振动信号的影响。
2)行星齿轮信号分离方法可以实现对行星齿轮振动信号进行充分的分离,能够有效诊断和定位行星轮的故障信号,无需较长采样周期,诊断准确率高。
3)试验验证结果表明,采用本方法对直升机动力传动系统进行故障诊断是可行的,对于降低飞行事故,保证飞行安全性是十分重要的。
[1]陈康,刘建新.直升机结构与系统[M].北京:兵器工业出版社,2007:129–132.
[2]Wu B,Saxena A,Khawaja T S,et al.An approach to fault diagnosis of helicopter planetary gears[C]//2004 IEEE Autotestcon,San Antonio,Texas,2004:475–481.
[3]Dong M,He D,Banerjee P,et al.Equipment health diagnosis and prognosis using hidden semi-Markov models[J]. The International Journal of Advanced Manufacturing Technology,2006(30):738–749.
[4]Chaari F,Fakhfakh T,Haddar M.Dynamic Analysis of a Planetary Gear Failure Caused by Tooth Pitting and Cracking[J].Journal of Failure Analysis and Prevention,2006(2):73–78.
[5]Blunta D M,Kellerb J A.Detection of a fatigue crack in a UH-60A planet gear carrier using vibration analysis[J].Mechanical Systems and Signal Processing,2006(20):2095–2111.
[6]Samuel P D,Conroy K,Pines D J.Planetary Transmission Diagnostics[R].NASA Glenn Research,NASA/CR - 2004 -213068.
[7]丁康,李巍华,朱小勇.齿轮及齿轮箱故障诊断实用技术[M].北京:机械工业出版社,2005:10–11,30–31.
[8]Blunt D M.Synchronous averaging epicyclic sun gear vibration:US,6898975 B2[P].2005 -05 -31.
[9]Braun S.The synchronous(time domain)average revisited[J].Mechanical Systems and Signal Processing,2011(25):1087–1102.
[10]Dalpiaz G,Rivola A,Rubini R.Effectiveness and sensitivity of vibration processing techniques for local fault detection in gears[J].Mechanical Systems and Signal Processing,2000,14(3):387–412.

