关于交换的弱归*-半环的研究

沈晓芹,田径,丰丕虎

(1.西安理工大学理学院,陕西西安 710054；2.西北大学数学系,陕西西安 710069)

关于交换的弱归*-半环的研究

沈晓芹1,田径1,丰丕虎2

(1.西安理工大学理学院,陕西西安 710054；2.西北大学数学系,陕西西安 710069)

研究了交换的弱归纳*-半环S上的二阶方阵半环S2×2.给出S2×2仍为弱归纳的一个充分条件.即若S2×2是λ-半环,则S2×2是弱归*-半环.应用这一结果可以证明S上的二元仿射映射存在最小的联立不动点,部分回答了相关文献中的公开问题.

λ-半环；*-半环；矩阵半环；最小联立不动点

1 引言及基本概念

半环是由德国数学家Dedekind在研究交换环的理想时提出的一种代数结构.自上个世纪六十年代开始,半环理论在Kleene,Eilenberg,Salomma等学者的推动下成为理论计算机科学中最重要的代数理论之一.

设S为非空集合.一个(2,2,0,0)型代数(S,+,·,0,1)是半环,记为S,如果

(i)(S,+)是可换的含幺半群,其中0是恒等元；

(ii)(S,·)是幺半群,其中1是恒等元且1/= 0；

(iii)对任意的a,b,c∈S有a·(b+c)=a·b+a·c,(b+c)·a=b·a+c·a；

(iv)对任意的a∈S有a·0=0·a=0.

以下对任意的a,b∈S,将a·b记为ab.

另一方面,不动点理论和与不动点的计算相关的课题在计算机科学的各个学科中都扮演着重要的角色.关于不动点的基本理论参见文献[2-4].

设P是偏序集,f是P上的映射.若有P中的元素x满足f(x)=x,则称x为f的不动点.若f的所有不动点组成的集合存在最小元,则记该最小元为λf；若P中的元素x满足f(x)≤x,则称x为f的前不动点.若f的所有前不动点组成的集合存在最小元,则记该最小元为µf.

设S是半环.若≤是S上的偏序关系,使S上的加法和乘法运算是单调的,则称S是偏序半环；若半环S上带有一个一元运算*:S→S(称为*运算),则称S是*-半环；若半环S既是偏序半环又是*-半环,则称它为偏序*-半环.

设S是半环.对任意a,b∈S,称映射fa,b:x→ax+b为S上的仿射变换.对任意a1,a2,b1∈S,称二元映射(x,y)→a1x+a2y+b1为S上的二元仿射变换.由于偏序半环上的加法和乘法是单调的,容易发现偏序半环上的仿射变换也是单调的.

随着计算机科学的发展,半环上连续映射的不动点受到人们的关注.著名学者Golan[5]指出:半环理论最重要的应用,主要体现在半环上仿射变换的不动点的相关性质.如,半环上仿射变换的不动点的存在性,唯一性及最小性.

2004年ˊEsik和Kuich[6]在Conway半环[7]的基础上将一些具有不动点性质的方程作为公理,并利用这些公理定义了归纳*-半环,进而推广了Kleene定理.2007年文献[8]同样利用方程的公理化方法定义了*-µ-半环和*-λ-半环.并借助它们解决了ˊEsik等人提出的一个公开问题,即:弱归纳*-半环上的形式幂级数半环仍是弱归纳的.

称偏序*-半环S为归纳*-半环[6],如果对任意的a,b∈S有:称满足积星恒等式与和星恒等式的半环为Conway半环.称偏序*-半环S为弱归纳*-半环,如果它满足不动点方程、和星恒等式以及弱不动点归纳法则:

引理1.1[6]弱归纳*-半环是Conway半环.

引理1.2[7]若S是Conway半环,则Sn×n也是Conway半环.

定义1.1[8]设S是偏序半环.对任意的a,b∈S,如果线性映射fa,b有最小不动点(前不动点),则称S为λ-半环(µ-半环).

文献[6]还提出下面的公开问题:若S是弱归*-半环,Sn×n是否仍为弱归纳*-半环?本文针对S是交换的弱归纳*-半环的情形,给出S2×2是弱归纳*-半环的一个充分条件,即:若S2×2是λ-半环,则它是弱归纳*-半环.利用这一结果研究了(Δ)的联立不动点.证明如果S2×2上的仿射变换存在最小不动点,那么S2×2有最小的联立不动点并且它就是文献[1]中构造的联立不动点.

2 矩阵

由S是弱归纳*-半环,有

定理2.1若S是交换的弱归纳*-半环,则以下命题等价:

(i)S2×2是λ-半环；

(ii)S2×2是*-λ-半环；

(iii)S2×2是弱归纳*-半环.

证明已经证明了(i)⇒(ii)成立.另外,由引理2.1知(iii)⇒(ii)成立.又因为*-λ-半环一定是λ-半环,所以(iii)⇒(i)成立.现在证明(ii)⇒(iii)成立.

设S是弱归纳*-半环.由引理1.1知,S是Conway半环.再由引理1.2知S2×2也是Conway半环.那么S2×2满足不动点方程(3)与和星恒等式(7).如果S2×2是*-λ-半环,那么对任意的A,B∈S2×2,A*B是方程AX+B=X的最小不动点.这就说明S2×2满足弱不动点归纳法则(8)式.故,S2×2是弱归纳*-半环.

3 联立不动点

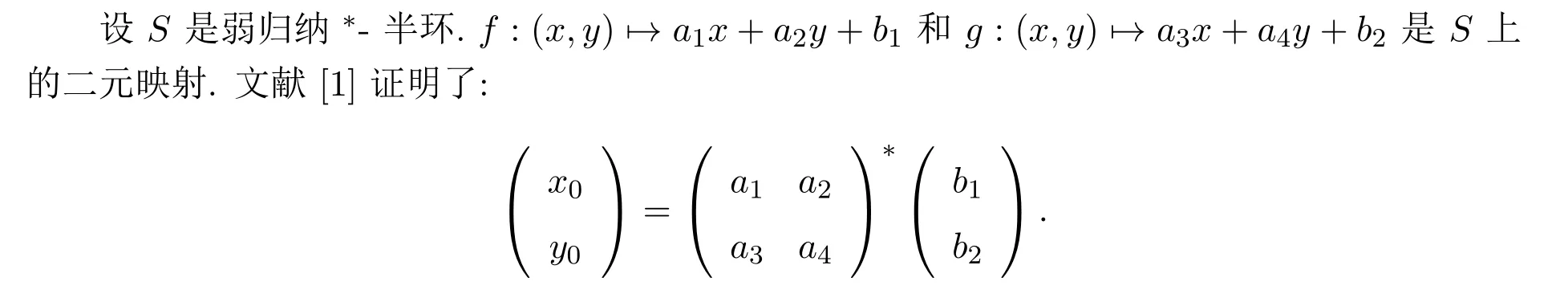
是f和g的联立不动点.进一步,由定理2.1知道它是f和g的最小联立不动点.即有

推论3.1设S是交换的弱归纳*-半环.如果S上的二元映射存在联立不动点,那么它们一定存在最小的联立不动点.

因此,部分地回答了文献[1]中提出的问题.

[1]冯锋,刘晓燕.弱归纳*-半环上仿射映射的联立不动点[J].数学进展,2008,37(3):283-290.

[2]Tarski A.A lattice-theoretical fixpoint theorem and its applications[J].Pacific Journal of Mathematics, 1955,5:285-309．

[3]Davis A.A characterization of complete lattices[J].Pacific Journal of Mathematics,1955,5:311-319.

[4]Abian A,Brown A.A theorem on partially ordered sets with applications to fixed point theorems[J].Canadian J.of Math.,1961,13:173-174.

[5]Golan J.The Theory of Semirings,with Applications in Mathematics and Theoretical Computer Science[M]. Harlow:Longman Scientific and Technical,1992.

[7]Conway J.Regular Algebra and Finite Machines[M].London:Chapman and Hall,1971.

[8]Feng F,Zhao X,Jun Y.B semirings and semirings[J].Theoretical Computer Science,2005,347:423-431.

On commutative weak inductive*-semirings

Shen Xiaoqin1,Tian Jing1,Feng Pihu2

(1.School of Scince,Xi′an University of technology,Xi′an710054,China； 2.Department of Mathematics,Northwest University,Xi′an710069,China)

The semiring S2×2of 2×2 matrices over a commutative weak inductive*-semiring S is studied.It is shown that if 2×2 is a λ-semiring then it is a weak inductive*-semiring again.Then the least simultaneous fixed points of two binary affine maps over S are given.

λ-semiring,*-semiring,matrices semirings,least simultaneous fixed points

O153.3

A

1008-5513(2012)04-0540-06

2011-02-10.

国家自然科学基金(11101330)；陕西省自然科学基金青年基金(2011JQ1007).

沈晓芹(1981-),博士,讲师,研究方向：代数及密码理论.

2010 MSC:16Y60