影响阻尼牛顿法收敛性的两个重要参数

张建军,李春泉,张烈辉

(1.西南石油大学理学院,四川成都 610500；2.西南石油大学石油工程学院,四川成都 610500)

影响阻尼牛顿法收敛性的两个重要参数

张建军1,李春泉1,张烈辉2

(1.西南石油大学理学院,四川成都 610500；2.西南石油大学石油工程学院,四川成都 610500)

对阻尼牛顿算法作了适当的改进,证明了新算法的收敛性.基于新算法,运用计算机代数系统Matlab,研究了迭代次数k,参数对(µ,λ)与初值x0三者间的依赖关系,研究了病态问题在新算法下趋于稳定的渐变(瞬变)过程.数值结果表明:(1)阻尼牛顿迭代中,参数对(µ,λ)与迭代次数k间存在特有的非线性关系；(2)适当的参数对(µ,λ)与阻尼因子α的共同作用能够在迭代中大幅度地降低病态问题的Jacobi阵的条件数,使病态问题逐渐趋于稳定,从而改变原问题的收敛性与收敛速度.

阻尼牛顿法；雅可比矩阵的条件数；病态问题；参数对(µ,λ)

1 引言

目前,非线性方程组求解的数值方法有Newton法,同伦型法,单纯形法与胞腔排除法[13].

牛顿迭代法是一种非常实用的计算方法,迭代公式如下:选择参数α的原则是使之满足:其中µ∈(0,1)为某定数,‖·‖表示向量或矩阵的任何一种范数.

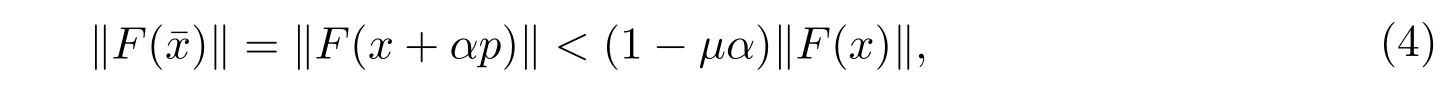
按(3)和(4)式进行迭代修正的方法称为阻尼牛顿法,参数α称为阻尼因子,当α=1时,就是牛顿法.牛顿法的显著缺点是,它是局部收敛的.它要求初始近似x0适当接近非线性方程组(1)的解x*,这个条件难以界定,阻尼牛顿法是基于下降算法,并具有大范围收敛性的一种迭代法.文献[4]给出了求解非线性方程组(1)的阻尼牛顿算法,并给出了特殊情形下阻尼牛顿法的大范围收敛性结果.文献[4]中涉及到两个重要参数µ,λ.但在文献所给算法的5个步骤中没有明确参数λ的作用；文献中关于算法的收敛性定理也与参数λ没有直接的关联.

本文结构安排如下:

第二节对文献[4]的算法作了适当的改进,证明了新算法的收敛性.新的算法与相应的收敛性定理均明确了参数µ与λ各自的作用与相互关系.第三节研究了阻尼牛顿迭代中迭代次数k,参数对(µ,λ)与初值x0三者间的关系；第三节还研究了病态问题在适当的参数对(µ,λ)和阻尼因子α的共同作用下趋于稳定的渐变(瞬变)过程.

2 主要结果

2.1 改进的阻尼牛顿算法

设µ,λ为固定的数,且满足

2.2 收敛性定理

下面证明,上述算法的第4步到第5步循环可在有限步内完成.

从而由(9)式推得(4)式对这个扩充的参数域成立.

这个定理指出,若F′(x)在D中非奇异,则阻尼牛顿法在每个迭代中,α仅改变有限多次.

3 数值试验

3.1 迭代次数k、参数对(µ,λ)与初值x0三者间的关系

为了考察新算法中参数µ与λ对迭代过程的影响,选择文献[4-5]中的非线性方程组为例加以说明.

例1考虑非线性方程组

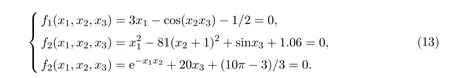
两组近似解分别为(0.4597,-0.9038,-0.5494)与(0.4404,-1.0948,-0.5546),精度要求:ε=10-5. (一)固定初值x0=(5,5,5)T,令参数对(µ,λ)取10种不同的线性关系(满足(5)式)

对每个参数对(µ,λ)计算取得近似解所需要的迭代次数k,参见图1.图中10条直线(与10条曲线相对应)反映的是参数µ与λ的不同线性关系,而10条曲线反映的是相应的直线上各点所对应的迭代次数.不同线性关系下的最小,最大迭代次数分别为7,10,11,12,13,15,17,19,24,33与282,286,294,495,533,564,591,1000,1000,1000.

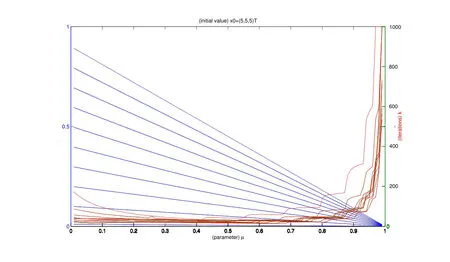
图1 迭代次数k、参数对(µ,λ)与初值x0的关系(1)

计算结果表明:①在不同线性关系中,l越小,取得近似解所需的迭代次数越小.②在不同线性关系中,参数对(µ,λ)与迭代次数k间存在相似的非线性关系,即随着直线的下降,迭代次数先减后增.在直线的前端或中部位置,迭代次数达到最小.在直线的末端,随着直线的下降,迭代次数剧烈增加.

(二)固定参数µ与λ的线性关系,令初值x0变化

在(14)式中取l=1/10.初值(x0,y0,z0)分别取为(5,5,5),(-5,-5,-5),(20,20,20),(-20, -20,-20).四种初值下的最小迭代次数分别为7,9,15与12(参见图2).计算结果表明:①初值越接近非线性方程组的解x*,取得近似解所需的迭代次数越小.②当初值偏离近似解较大时,参数对(µ,λ)与迭代次数k的依赖关系可能会出现较大的波动,如初值为(20,20,20),(-20,-20,-20)时,出现迭代次数超过1000的情形.

图2 迭代次数k、参数对(µ,λ)与初值x0的关系(2)

值得注意的是,即使是对应同一初值,在某些参数对(µ,λ)下,迭代过程收敛于(0.4404, -1.0948,-0.5546)；而在另一些参数对(µ,λ)下,迭代过程收敛于(0.4597,-0.9038,-0.5 494).

为了说明新算法相对于牛顿法的优越性,应用牛顿法求解例1给出的非线性方程组.在初值(5,5,5),(-5,-5,-5),(-20,-20,-20)下牛顿法收敛,迭代次数分别为9,9,11.与阻尼牛顿法相比,牛顿法的收敛速度更快.原因是上述初值下,牛顿迭代中方程组并没有出现奇异或数值稳定性问题.在初值(20,20,20)处,由于牛顿迭代中第一次近似解的雅可比矩阵的条件数为无穷大,计算机停止计算,牛顿法失败.此时,阻尼牛顿法显示出了优越性,如图2所示,在100对(µ,λ)中,97对收敛且迭代次数均小于400,最小迭代次数为15.

3.2 病态问题趋于稳定的渐变(瞬变)过程分析

由于函数F在近似解处的Jacobi阵的条件数的大小能够反映方程组的数值稳定性.因此,本文通过计算条件数跟踪研究了新算法下病态问题趋于稳定的渐变(瞬变)过程.

例2继续研究例1中的非线性方程组.如前所述,在牛顿迭代中,一旦初值远离所给非线性方程组的解x*,牛顿法就可能失败.表1给出了4组初值下牛顿迭代的计算结果(其中:ck=cond(F′(xk)),k=1,2,···表示第k次近似解的Jacobi阵的条件数).所列4组初值下牛顿法不收敛.原因之一是计算的稳定性,第一次迭代后,它们的近似解的Jacobi阵的条件数都很大(或由于Jacobi阵的某些元素为无穷大而使计算机无法确定其条件数),导致了计算过程的不稳定.因此,它们均属于病态问题.另一个原因是计算的效率问题,根据文献[6-8],当函数F在近似解处的Jacobi阵的条件数很大时,可能导致迭代中产生很小的步长,从而降低算法的效率.

表1 牛顿迭代中的病态问题举例

新算法下,上述病态问题都能在15步之内取得满足误差精度的近似解.跟踪计算了收敛过程中条件数ck的变化状况.计算结果见表2.通过对该表的观察与对比,发现条件数的变化呈现出一定的规律性:①通过选择适当的参数对(µ,λ)及对阻尼因子α的调整,使得第一次近似解的Jacobi阵的条件数都得到大幅度地下降.②从第二步迭代开始,各次近似解的Jacobi阵的条件数以两种方式下降,直至收敛.对某些病态问题(如P01等),迭代中Jacobi阵的条件数逐渐变小(单调下降方式或小幅波动下降方式)而使迭代过程收敛.而对另一些病态问题(如P02、P03、P04等),Jacobi阵的条件数先逐渐变大,达到最大值后,陡然变小而使迭代过程收敛.

表2 阻尼牛顿迭代中条件数ck的变化状况

参考文献

[1]Xu Z B,Zhang J S,Wang W.A cell exclusion algorithm for determining all the solutions of a nonlinear system of equation[J].Appl.Math.and Computation,1996,80:181-203.

[2]Zhang J S,You Z Y,Xu Z B.A cell method for finding all solutions of a nonlinear equations and optimization problems[J].Math.Numerica Sinica,1994,16:195-203.

[3]孟彪龙,邢志栋.非线性方程组求全部解的胞腔排除法[J].纯粹数学与应用数学,1999,15(2):72-76.

[4]黄象鼎,曾钟钢,马亚南.非线性数值分析的理论与方法[M].武汉:武汉大学出版社,2004.

[5]施妙根,顾丽珍.科学和工程计算基础[M].北京:清华大学出版社,1999.

[6]Deuflhard P.A modified Newton method for the solution of ill-conditioned systems of nonlinear equations with applications to multiple shooting[J].Numer.Math.,1974,22:289-315.

[7]曾金平,刘星果.自然水平函数在求解病态非线性方程组的阻尼牛顿法中的应用[J].湖南大学学报:自然科学版,2003,30(1):8-10.

[8]周硕,郭丽杰,吴柏生.Jacobi迭代预处理的条件数与迭代次数的关系[J].东北电力学院学报,2003,23(6):57-60.

The effect of two important parameter upon the convergence in damped Newton method

Zhang Jianjun1,Li Chunquan1,Zhang Liehui2

(1.College of Science,Southwest Petroleum University,Chengdu610500,China； 2.College of Petroleum Engineering,Southwest Petroleum University,Chengdu,610500China)

In this paper,the damped Newton method is improved suitably and the convergence for new method is proved.Based on the new algorithm,a program is proposed and fulfilled by numerical and symbolic computations in Matlab,we study the relation among the iteration degrees k,parameters(µ,λ)and initial value x0.We also study the gradual(transient)process of the ill-conditioned systems nonlinear equations tending stable.Numerical results show that there is a special nonlinear relation between the parameters(µ,λ)and the iteration degrees k for damped Newton method and that the suitable parameters(µ,λ)and damping coefficient α can greatly decrease condition number of Jacobi matrix of ill-conditioned systems nonlinear equations.The ill-conditioned problems can gradually become stable and thus the convergence and the convergence speed of the ill-conditioned systems nonlinear equations can be changed.

damped Newton method,condition number of the Jacobi matrix, ill-conditioned systems equations,parameters(µ,λ)

O241.7

A

201109018(2012)04-0433-07

2011-09-24.

四川省教育厅2011年重点科研项目(10ZA073).

张建军(1958-),博士,副教授,研究方向：石油工程信息分析与处理.

2010 MSC:65k05,90C30