一种具有预测功能的抗积分饱和PI速度控制器

周华伟， 温旭辉， 赵峰， 张剑

(1.中国科学院电工研究所，北京100190;2.江苏大学电气信息工程学院，江苏镇江212013;3.中国科学院 研究生院，北京100190)

0 引言

永磁同步电机以其高效率、高功率密度和高转矩/惯量比特性在调速系统中得到了广泛的应用。传统PI控制算法简单、鲁棒性好、可靠性高、易于实现，因此速度控制一般采用PI策略［1］，但是由于传统PI的设计是根据系统局部区域线性化设计的，忽略了饱和区的非线性。在线性区对给定小阶跃以及小负载扰动很有效;若给定大阶跃，PI往往饱和而工作于非线性区，但PI仍按线性区调节，必然导致大的超调、震荡、响应速度变慢等问题［2］。为追求系统的动态响应速度，需要较大的Kp，为防止积分饱和而引起超调，Ki一般很小甚至为零;为确保系统的稳态性能，希望较大的Kp和Ki。因此对于传统PI，一套固定的PI参数无法解决系统稳态性能与动态性能、响应快速性和超调量、跟踪与抗扰等方面的矛盾［3］;若采用多套PI，理想的切换点须反复实验方能获取。

为改善传统PI的不足，学者们提出了不同的策略。变参数 PI［1］根据误差大小及时调整 PI参数;非线性 PI［4－5］通过非线性函数确定 PI参数;模糊PI［6－7］由模糊控制器根据误差和误差的变化率实时整定PI参数。虽然这些方法经过反复试验能整定出合适的PI参数，获得理想的性能，但是以牺牲响应速度换取零超调的。积分分离PI［8］根据误差大小在合适的切换点切换P模式和PI模式，但切换点的选择得通过反复试验获得或者转矩指令的在线频谱分析得到。IP控制［9］使系统传递函数的分子中不含微分项，因此当给定阶跃时能有效削弱超调的发生，但其动态响应速度需加快。滑模变结构控制［10－11］根据系统当前状态有目的地调节，迫使系统按预定状态轨迹运动，但是在稳态时系统输出转矩存在高频抖振现象，这可能导致机械共振。抗积分饱和PI［12］在积分器饱和时，限制积分器作用。经典的抗积分饱和PI算法有:条件积分 PI［2］;回溯算法 PI［13－14］等。尽管该策略充分利用了线性系统控制理论和设计方法，但是由于采用分步法设计原则，系统稳定性和动态性能缺乏预见性［15］。

文献指出非线性校正装置能成功解决快速性和振荡度之间的矛盾。本文在传统PI中引入非线性思想，提出一种具有预测功能的抗积分饱和PI速度控制策略，且将其和传统PI以及回溯算法PI在两台额定功率为20 kW的永磁同步电机(permanent magnet synchronous motor，PMSM)构成的对拖台架上进行对比实验。实验结果表明该策略具有更好的动态性能且能保留传统PI的鲁棒性能以及稳态性能。

1 具有预测功能的抗积分饱和PI速度控制

1.1 控制策略的提出

电机期望的调速性能是:速度给定阶跃时，系统响应快速且无超调，即在远离目标转速时能以最快的加速度趋近目标，而当离目标较近时其响应速度以负指数规律衰减，如图1所示。

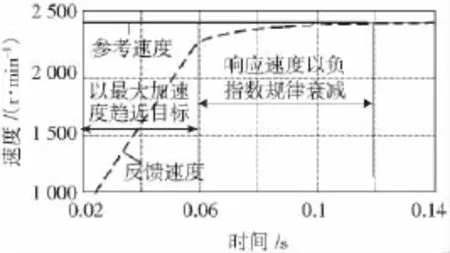
图1 给定阶跃时速度调节器期望性能示意图Fig.1 The expected performance of speed controller when the reference steps

PI控制器不但在系统中引入了一个纯积分环节，而且还引进了一个开环零点。纯积分环节能有效地改善系统的稳态性能，零点有助于改进系统的稳定性能。PD控制器的优点“提前性”、“预见性”［16－17］不但能反映误差信号的变化趋势，而且能在误差信号尚未出现之前就在系统中发出一个有效的早期修正信号，从而有助于系统的稳定，并抑制过大的超调量;但微分存在着将高频干扰信号同时放大的缺点，因此微分控制较少使用。

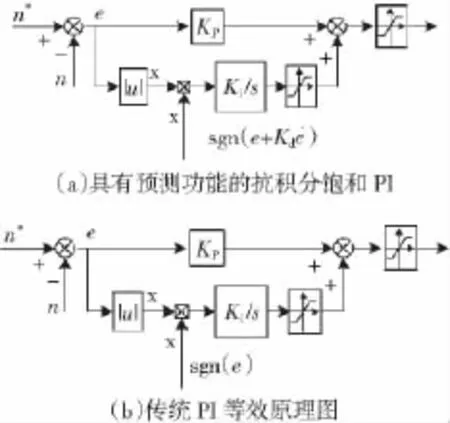
图2 PI控制器Fig.2 PI controller

吸取PD控制器的优点，消除PI控制器的缺点，设计具有预测功能的抗积分饱和PI控制器，原理图如图2(a)所示。传统PI原理图可等效为图2(b)，可见本文所设计PI和传统PI唯一区别就是积分方向的控制，其利用PD预测性能，根据PD输出值的符号决定积分方向。系统在响应给定阶跃的过程中，当e(t)较小时积分器能及时反向积分，而不是等e(t)方向改变了才反向积分，实现了积分器的提前退饱和，大大减小了系统的超调机率。文献［18］指出积分作用可以一定程度的削弱高频开关导致的抖振现象，由于PI中含有积分项，能抑制PD频繁改变符号导致的抖振现象。

1.2 速度控制器设计和性能分析

电机转速环控制系统框图如图3所示，电机运动方程［10］为

式中:J是电机转动惯量;ω电机转速，单位rad/s;B是粘滞阻尼系数;TL是负载转矩;KT是转矩电流系数;i(t)是电机电流。

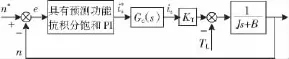
图3 具有预测功能的抗积分饱和PI系统框图Fig.3 The system block diagram of the predictive antiwindup PI

转速误差e(t)以r/min为单位，忽略粘滞阻尼系数，则由式(1)得

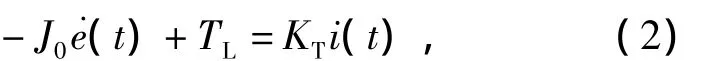
电流环动态响应速度远快于速度环，因此电流的动态响应速度可以忽略，认为电流完全跟随，Gc(s)=1。设转速环PI控制器输出上限为SL，下限为－SL。当给定转速n*正向大阶跃时，PI控制器饱和输出SL，由式(2)求得e(t)为

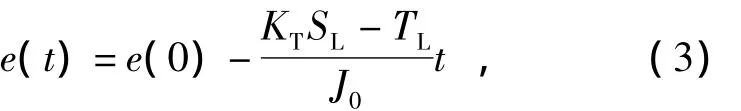
式中e(0)是初始转速误差。

由于所设计PI中积分方向由sgn(e+Kd˙e)决定，当e＞－Kd˙e时，积分方向由sgn(e)决定，此时所设计PI和传统PI一样，因此只要选择合适的PI参数就能保证系统稳定;当e＜－Kd˙e，积分方向由sgn(Kd˙e)控制。为保证系统在适当的时候既能及时退出饱和，又不影响系统的性能，应选择合适的Kd。式(4)决定了积分方向变换点。

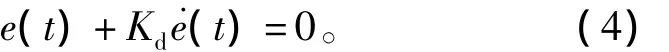
将式(3)代入式(4)得积分项退饱和时的转折点为

由式(4)知t1后积分方向改由sgn(Kd)控制，积分项开始退饱和，但是由于PI控制器中比例项的作用，PI控制器仍处于饱和状态，于是e(t)继续按式(3)减小，只有当积分项退饱和部分的绝对值等于比例项时，PI才处于退饱和临界点，于是有

式中积分起始点为式(5)中(t1，e(t1))。

将式(3)代入式(6)，得PI控制器退饱和临界点为

由此可见要加快系统的响应速度，应充分利用PI饱和。由式(7)知，PI参数决定了系统使用PI饱和的时间和退饱和时剩余转速误差。

当PI退出饱和后，PI才起作用，此时积分方向仍由sgn(Kd˙e)控制，积分项继续反向积分，PI输出减小，于是以(t2，e(t2))为原点，系统方程为

由式(8)求得误差转速，反拉氏变换后得

式中:

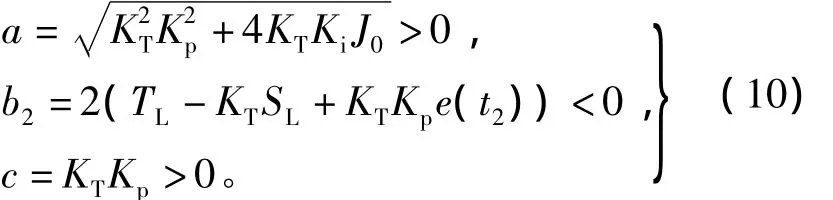
由式(9)得

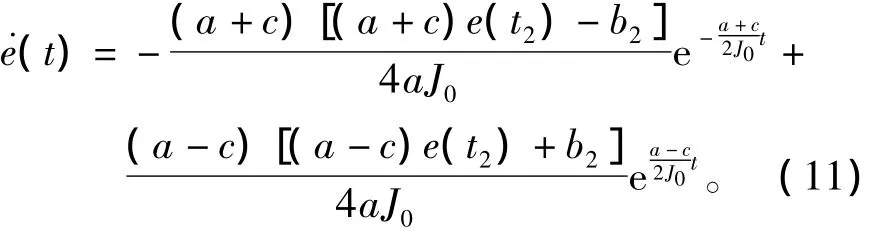
根据式(10)可证明(a+c)e(t2)－b2＞0成立。

在积分方向由sgn(Kd)控制时，为保证积分方向能变为sgn(e)控制，系统进入传统PI，要求e+Kd˙e＞0，于是由式(9)和式(11)得

根据前面分析，式(12)第一项绝对值为递减指数函数，第二项绝对值为递增指数函数，因此要使式(12)在t2后再经一段时间t方成立，只有

由式(7)、式(10)求得式(13)成立的条件为

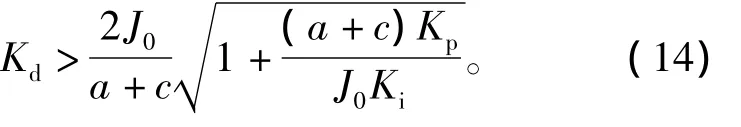
由式(12)求得时间t

因此当Kd满足式(14)时，PI积分方向能由sgn(Kd˙e)控制变为sgn(e)控制，系统能进入传统PI控制。在传统PI控制中，当PI比例部分减小量的绝对值小于积分部分增加量的绝对值时PI输出增加，˙e(t)增加，e(t)减小，当满足e(t)+Kd˙e(t)＜0时，积分方向改由sgn(Kd˙e)控制。如此按式(5)不断变换积分方向，使e(t)按式(16)趋于零，实现了无超调控制，如图4所示。

式中:e(t3)是积分器退出饱和后积分方向开始由sgn(e)决定时的转速误差。

图4 本文所提PI工作原理示意图Fig.4 The schematic diagram of the proposed PI

由式(16)知Kd的大小直接决定着e(t)趋于零的速度，Kd越小，系统响应速度越快，但是其响应速度不可能超过其最大加速度，因此Kd不能无限减小，同时Kd受式(14)的限制。因此

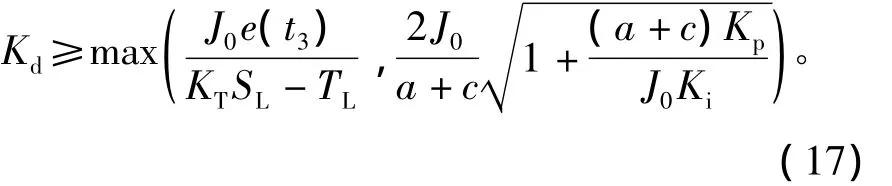
同样可推出当给定转速负向大阶跃时，e(t)的变化情况与正向时相同，只是符号相反。

因此该预测功能的抗积分饱和PI控制器能将系统响应的快速性和无超调完美地结合起来。系统控制框图如图所示。

图5 系统控制框图Fig.5 System control diagram

1.3 稳定性证明

本文所设计的PI控制器不饱和时输出电流指令值为

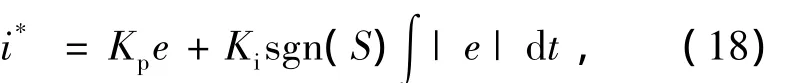
选择李亚普诺夫函数V=0.5S2，由李亚普诺夫稳定性理论得

根据式(1)、式(2)和式(18)按式(19)要求得

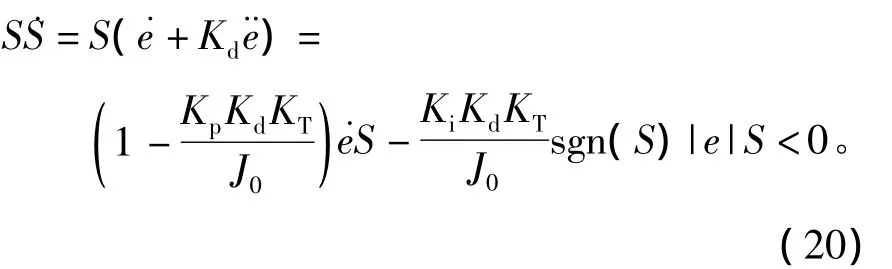
由此可见当˙eS＜0时，系统会自动调整S的方向使˙eS＞0。

2 实验验证

为验证本文所设计的具有预测功能的抗积分饱和PI速度控制器性能，使用两台额定功率为20 kW的PMSM搭建了对拖台架，进行了恒负载转矩下转速阶跃实验和恒转速下负载转矩阶跃实验，且和传统PI以及如图6所示的回溯算法PI进行了实验对比。

PMSM参数为:额定功率 20 kW，额定转速2 500 r/min，极对数3，定子相电阻26 mΩ，d轴电感0.52 mH，q轴电感1.02 mH，永磁磁链0.129 Wb。实验中母线电压为320 V，最大转矩/电流角δ设定为20度，PI参数见表1。转速使用NI CAN卡记录，电流波形采用PEMUK罗氏线圈CWT1和泰克示波器DPO3054测量。

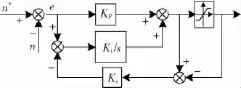
图6 回溯算法PIFig.6 Anti-windup PI based on tracking back calculation scheme

表1 PI参数Table 1 PI parameters

在负载为70 N·m时按表2进行转速阶跃实验。由图7～图9知使用传统PI速度控制策略转速从1 000 r/min阶跃到2 500 r/min需要1.5 s且存在365 r/min的超调，从2 500 r/min阶跃到1 000 r/min需要1.4 s且存在35 r/min的超调;尽管回溯算法PI解决了超调问题，但是需要的调速时间仍然较长;而采用本文提出的PI速度控制策略调速时间分别为0.86 s和0.76 s，大大的缩短了调速时间，同时解决了速度超调的问题，另稳态时不存在稳态误差。由电流波形分析得到本文提出的PI速度控制策略有效地利用了PI饱和特性，适当地延长了系统最快响应速度段的时间;同时该PI策略能及时退出积分饱和，使转速误差以负指数规律衰减为零，避免了超调的发生。因此本文提出的PI算法具有优良的动态响应品质，在满足无超调的同时实现了系统的快速响应，且具有良好的稳态性能。

表2 负载为70 N·m速度给定阶跃Table 2 Steps of reference speed at TL=70 N·m

为进一步验证本文提出的PI控制策略的抗负载扰动的鲁棒性能，按表3在2 500 r/min转速下进行了负载转矩阶跃实验。由图10～图12知负载转矩在25 N·m和95 N·m之间阶跃时，3种PI速度控制器都能把电机转速波动控制在160 r/min以内;传统PI控制策略和回溯算法PI控制策略使电机转速恢复用时均为1.18 s和1.04 s，而本文提出的 PI策略需1.22 s和1.1 s使电机转速恢复，因此本文提出的PI控制策略使电机转速恢复时间略长于传统PI和回溯算法PI，主要原因是由于在该情况下本文提出的PI控制策略没能利用PI饱和特性，另外在趋近稳态过程中是以负指数规律趋近的。由此可见基于预测功能的抗积分饱和PI速度控制器保留了传统PI的鲁棒性。

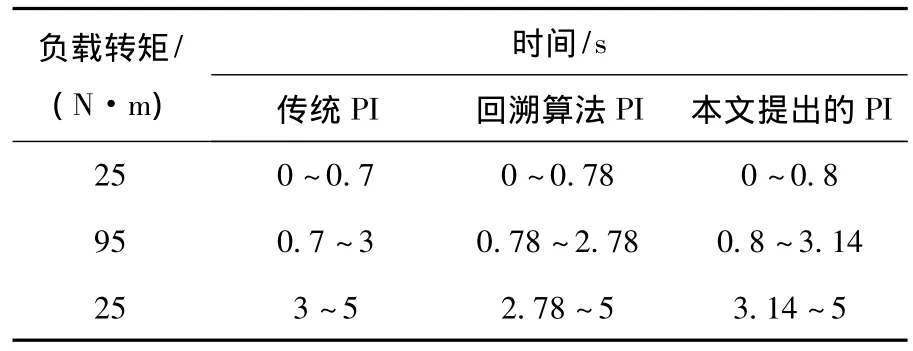
表3 转速2 500 r/min时负载转矩突变Table 3 Steps of load torque at n*=2 500 r/min

图7 传统PI速度响应性能Fig.7 Speed response performance with the traditional PI

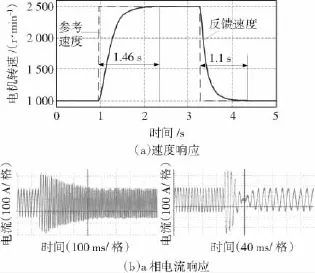
图8 回溯算法PI速度响应性能Fig.8 Speed response performance with PI based on tracking back calculation scheme

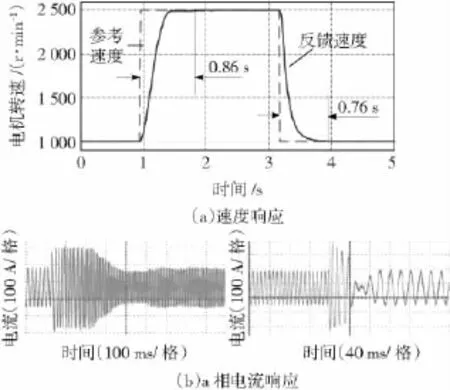
图9 本文提出的PI速度响应性能Fig.9 Speed response performance with the proposed PI

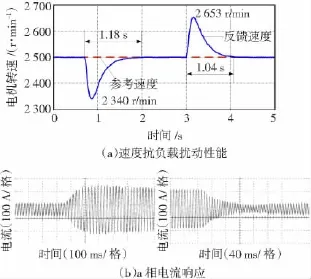
图10 转矩突变时传统PI速度控制器速度抗扰性能Fig.10 Speed anti-disturbance performance with the traditional PI

图11 转矩突变时回溯算法PI速度控制器速度抗扰性能Fig.11 Speed anti-disturbance performance with PI based on tracking back calculation

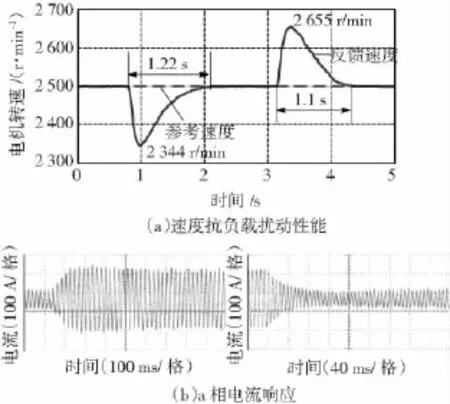
图12 转矩突变时本文设计的PI速度控制器速度抗扰性能Fig.12 Speed anti-disturbance performance with the proposed PI

3 结论

1)传统PI利用积分饱和作用加快系统响应速度会导致超调，而本文提出的具有预测功能的抗积分饱和PI速度控制策略有效地利用了积分饱和作用，加快了系统响应速度;同时利用PD的预测功能，在误差为零前，及时调整积分方向，退出积分饱和，避免了超调的发生。

2)理论分析和实验验证了该策略能使转速快速跟随，无超调、不震荡、无稳态误差，且保留了传统PI的鲁棒性能和稳态性能。

3)该策略只使用一套PI参数，参数整定比较方便。

4)将该策略用于搭载机械式自动变速器(AMT)的纯电动汽车中的驱动电机调速控制，能满足AMT换挡品质的要求，即要求驱动电机具有调速的快速性、无超调等动态品质。

［1］ 孙强，程明，周鹗，等.新型双凸极永磁电机调速系统的变参数PI控制［J］.中国电机工程学报，2003，23(6):117－122.

SUN Qiang，CHENG Ming，ZHOU E，et al.Variable PI control of a novel double salient permanent magnet motor drive［J］.Proceedings of the CSEE，2003，23(6):117 －122.

［2］ CHOI Jongwoo，LEE Sangcheol.Antiwindup strategy for PI－ type speed controller［J］.IEEE Transactions on Industrial Electronics，2009，56(6):2039－2046.

［3］ 张平化，杨贵杰，李铁才.三相电压型PWM整流器的二自由度I-PD电压控制［J］.电机与控制学报，2009，13(5):667－672.

ZHANG Pinghua，YANG Guijie，LI Tiecai.Two-degree-of-freedom I-PD voltage control of three-phase PWM VSR［J］.Electric Machines and Control，2009，13(5):667 －672.

［4］ 王江，王静，费向阳.永磁同步电动机的非线性PI速度控制［J］.中国电机工程学报，2005，25(7):125－130.

WANG Jiang，WANG Jing，FEI Xiangyang.Nonline PI speed control of permanent magnetic synchronous motor［J］.Proceedings of the CSEE，2005，25(7):125－130.

［5］ 王莉，曹小庆，张卓然，等.电励磁双凸极无刷直流发电机非线性PI调压技术的研究［J］.中国电机工程学报，2006，26(5):153－158.

WANG Li，CAO Xiaoqing，ZHANG Zhuoran，et al.Research of nonlinear PI voltage regulation for doubly salient brushless DC generator［J］.Proceedings of the CSEE，2006，26(5):153 －158.

［6］ CHEN Ming，SUN Qiang，ZHOU E.New self-tuning fuzzy PI control of a novel doubly salient permanent-magnet motor drive［J］.IEEE Transactions on Industrial Electronics，2006，53(3):814－821.

［7］ 李兵强，林辉.新型永磁同步电机高精度调速系统［J］.中国电机工程学报，2009，29(15):61 －66.

LI Bingqiang，LIN Hui.Novel high － precision speed regulation system for permanent magnet synchronous motor［J］.Proceedings of the CSEE，2009，29(15):61－66.

［8］ SEOK Julki，KIM Kyungtae，LEE Dongchoon.Automatic mode switching of P/PI speed control for industry servo drives using online spectrum analysis of torque command［J］.IEEE Transactions on Industrial Electronics，2007，54(5):2642 －2647.

［9］ 郭新华，温旭辉，赵峰，等.基于电磁转矩反馈补偿的永磁同步电机新型IP速度控制器［J］.中国电机工程学报，2010，30(27):7－13.

GUO Xinhua，WEN Xuhui，ZHAO Feng，et al.A novel IP speed controller of PMSM based on electromagnet torque feedback compensation［J］.Proceedings of the CSEE，2010，30(27):7 －13.

［10］ ZHOU Huawei，WEN Xuhui，ZHANG Jian，et al.Sliding mode speed control for interior permanent magnet synchronous machine based on variable exponential reaching law［C］//Proceeding of the 13th International Conference on Electrical Machines and Systems，October 10 － 13，2010，Incheon，Korea.2010:1020－1023.

［11］ 方斯琛，周波.滑模控制的永磁同步电机伺服系统一体化设计［J］.中国电机工程学报，2009，29(3):96 －101.

FANG Sichen，ZHOU Bo.Integrated design for permanent magnet synchronous motor servo systems based on sliding mode control［J］.Proceedings of the CSEE，2009，29(3):96 －101.

［12］ ZHANG Da，LI Hui，COLLINS E G.Digital anti－ windup PI controllers for variable-speed motor drives using fpga and stochastic theory［J］.IEEE Transactions on Power Electronics，2006，21(5):1496－1501.

［13］ OHISHI K，HAYASAKA E，NAGANO T，et al.High-performance speed servo system considering voltage saturation of a vectorcontrolled induction motor［J］.IEEE Transactions on Industrial Electronics，2006，53(3):795 －802.

［14］ VISIOLI A.Modified anti-windup scheme for PID controllers［J］.IEE Proceedings-Control Theory and Applications，2003，150(1):49－54.

［15］ 杨明，徐殿国，贵献国.永磁交流速度伺服系统抗饱和设计研究［J］.中国电机工程学报，2007，27(15):28－32.

YANG Ming，XU Dianguo，GUI Xianguo.Study of AC PMSM speed servo system anti-windup design［J］.Proceedings of the CSEE，2007，27(15):28 －32.

［16］ 高国燊，余文烋.自动控制原理［M］.广州:华南理工大学出版社，2001:113 －116，360.

［17］ KRISTIANSSON B，LENNARTSON B.Robust tuning of PI and PID controllers:using derivative action despite sensor noise［J］.IEEE Control Systems Magazine，2006，26(1):55－69.

［18］ 刘颖，周波，方斯琛.基于新型扰动观测器的永磁同步电机滑模控制［J］.中国电机工程学报，2010，30(9):80－85.

LIU Ying，ZHOU Bo，FANG Sichen.Sliding mode control of PMSM based on a novel disturbance observer［J］.Proceedings of the CSEE，2010，30(9):80 －85.