一种改进型超前角弱磁控制算法

于家斌， 秦晓飞， 郑军， 王云宽

(中国科学院自动化研究所，北京100190)

0 引言

永磁同步电机是数控机床的核心部件，其高速化是数控系统发展的主要趋势之一［1］。为了满足对各种工件的加工要求，在逆变器容量一定的情况下永磁同步电机不但应有较宽的调速范围，而且应在高速时具有较强的带载能力。因而，其弱磁控制策略成为目前研究的热点之一。

针对永磁同步电机的弱磁控制，国内外一些学者分别提出了六步电压法，电流调节器法，自适应弱磁控制法，非线性降维观测器法等弱磁控制策略［2－5］。但是这些方法都较为复杂，实现困难。在此基础上，一些学者提出了便于实现的改进型方法，例如利用d，q轴电流和电压外环输出的电压差修正电流设定值的方法，简化的电压控制算法，基于气隙磁场定向的弱磁控制算法，超前角弱磁控制算法等［6－9］。然而针对提高弱磁阶段电机带载能力研究的相关文献却比较少。

超前角弱磁控制算法是目前较为常用的弱磁控制方法［9］。运用该算法控制表贴式永磁同步电机运行于弱磁区时，随着负载的增加，通常会出现如下问题:从恒转矩区到恒功率区的过渡过程中，出现较大的电流震荡，从而引起速度波动，系统的动态性能变差。而在恒功率区，会出现稳态速度下降的现象，稳态时的速度和电流波动也会变大，系统的稳态性能不佳。

为此，本文在分析传统超前角弱磁控制算法原理的基础上，提出了一种改进型超前角弱磁控制算法，并通过实验结果验证了算法的正确性和有效性。

1 表贴式永磁同步电机数学模型及传统超前角弱磁控制算法

d－q轴系下表贴式永磁同步电机定子电压方程［10］为

式中:Ld和Lq分别为直轴和交轴同步电感，且Ld=Lq，Rs为定子相电阻，ωr为转子的电角速度，ψf为转子永磁体产生的励磁磁场的基波磁链。

电机高速稳定运行时，忽略定子压降，电压方程可以改写为

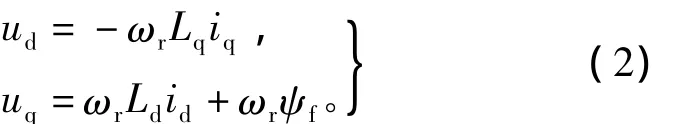
由式(3)可以看出，当电机定子电压达到逆变器的输出极限时，为了使转速ωr升高，只能通过增加直轴去磁电流分量id和减小交轴电流分量iq，以维持电压平衡，达到弱磁调速的目的。

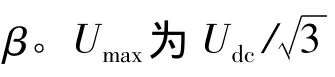
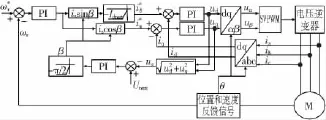
图1 传统超前角弱磁算法框图Fig.1 Block diagram of traditional leading angle flux weakening control algorithm

2 改进的SVPWM过调制算法

表贴式永磁同步电机采用传统超前角弱磁控制算法加载运行时，当给定电机转速超过其转折速度，在其升速阶段，会出现d，q轴电流的剧烈震荡，如图2所示，进而导致速度的波动，电机没有实现从恒转矩区到恒功率区的平滑过渡。电流的剧烈震荡通常会引起驱动器的过流保护，同时引发逆变电路较大的di/dt和dv/dt，增大电机运行时的电磁干扰，降低功率器件的使用寿命。通过分析得出在弱磁调速的升速阶段，电流环的输出即电压指令值在某些瞬间会超过SVPWM算法的输出范围，由于PI调节器固有的延迟性，依靠弱磁控制的电压闭环并不能快速地将电压调整过来，从而造成了输出电压在某些瞬间不可控，引起了电流的震荡。为此，本文尝试采用一种改进的SVPWM过调制算法，在逆变器直流侧电压不变的情况下增大其交流电压输出，提高电压输出能力［11］，改善弱磁调速时的动态性能。

图2 d，q轴电流震荡波形图Fig.2 The vibration waveforms of d，q currents

SVPWM的基本原理为在PWM载波周期Tpwm内，利用相邻的两个基本电压矢量的时间线性组合来模拟参考电压矢量。以第0扇区为例，给定矢量Ur=T1U(100)+T2U(110)，其中 T1，T2分别是U1(100)和U2(110)矢量的作用时间，如图3所示。一般情况下要将参考电压矢量圆整到正六边形内切圆的范围内，以保证输出不超出正六边形的范围。

图3 SVPWM空间电压矢量图Fig.3 Diagram of SVPWM voltage space vector

当参考电压矢量的幅值超出正六边形范围时，必须对其进行调整，使其限制到正六边形范围内。文献［12］和［13］提出的过调制算法首先根据参考电压的大小判断所在的过调制区域，然后根据区域不同对其进行调整，根据调整后的电压采取不同的控制策略计算各个基本电压矢量的作用时间。由于上述算法主要是针对开环系统的，必须保持输出电压基波与参考电压相符。对参考电压的调整主要采用查表计算，这种方法需要预先在控制器中存储大量的数据，不利于工程实现。对于闭环矢量控制系统，可以依靠电流调节器的作用自动对参考电压进行调整，使输出电压基波满足要求。因此可以在不要求输出电压基波和参考电压相一致的前提下对上述SVPWM过调制方法进行改进，图4为改进的过调整算法流程图。

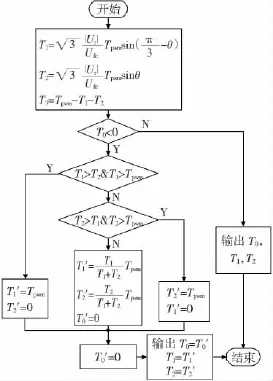
图4 改进的过调制算法流程图Fig.4 Flow chart of improved over modulation algorithm

在过调制区I，以电压零矢量作用时间T0是否小于零作为过调制起始点的判断依据，当指令电压矢量的轨迹位于正六边形外接圆和正六边形之间时，将原指令电压轨迹超出正六边形的部分校正到正六边形的边上，不改变给定电压矢量的相位而直接将矢量幅值截短来实现过调控制。在过调制区II，零矢量作用时间T0始终为负值，首先设定T0为0，利用6个基本矢量和正六边形的边进一步增大输出基波的幅值。在基本矢量上停留的时间越长，输出的电压基波幅值越大。当每个基本矢量上停留的时间达到六分之一周期时，输出电压为6拍阶梯波。

3 基于q轴电流误差的超前角弱磁控

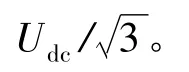
通过对传统超前角弱磁控制算法的原理分析可以得出，虽然增加Umax的取值可以使弱磁时输出的电压指令值变大，但是此时指令电压已经接近甚至超出逆变器的输出范围，会导致输出电压的不可控状态，从而引起速度和电流的震荡，造成系统的不稳定。

由于弱磁时的电压闭环限制了电机定子的输入电压，从而导致恒功率阶段稳态速度的下降，因此，本文提出使用q轴电流误差闭环代替电压闭环的超前角弱磁控制算法，来提高弱磁控制时的稳态性能。

电机在转折速度以下时，由于电流环PI调节器的作用，iq与其指令值iq*的偏差iqerr几乎等于零。但是随着速度的升高，当电机端电压达到逆变器所能提供的最高电压时，PI调节器进入饱和状态，失去调节电流的能力，使电流环失去控制，iqerr明显增大。因此可以将偏差iqerr作为开启弱磁控制的条件。图5为基于q轴电流误差的超前角弱磁控制框图。

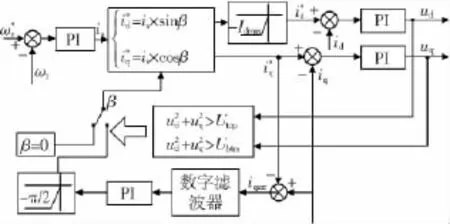
图5 基于q轴电流误差的超前角弱磁控制框图Fig.5 Block diagram of leading angle flux weakening control based on q axis current error

在图5所示的弱磁控制系统中，设置了一个基于q轴电流误差的反馈环节来进行弱磁控制。首先用局部平均窗口对 iqerr进行数字滤波，消除由于PWM斩波引起的高频噪声干扰。将滤波后的iqerr输入PI调节器产生超前角β，来计算产生新的id和iq。理论上，在转折速度以下，iqerr=0，但是在实际系统中，即使经过了数字滤波，可能iqerr≠0。经过PI调节器之后，其输出的id≠0，并没有实现在恒转矩区对电机的最大转矩/电流控制。为避免上述问题，实现在转折速度以下β=0，不开启弱磁控制，在转折速度以上，β由PI调节器输出产生，本算法将+与开启弱磁的上限值Utop和下限值Ubtm进行比较，当其大于Utop时，超前角β采用PI调节器的输出值，当其小于Ubtm时，令超前角β=0。Utop和Ubtm的取值根据实际经验进行选择。同样在弱磁调速时，仍要限制id使其小于电机的最大去磁电流。

4 实验结果

为了验证本文提出的算法的有效性，本文设计了基于数字信号处理器(digital signal processor，DSP)的全数字永磁同步交流伺服实验平台。DSP选用TI公司的 TMS320LF2812，逆变器采用 MITSUBISHI公司的PM75RSA120，PMSM的主要参数:额定功率3.2 kW，额定电压300V，额定电流6.8 A，额定转速2 000 r/min，静力矩16 N·m，电压常数144 V/1000 r·min－1，电机极对数3，转子惯量26.7 ×10－4kg·m2。

图6 TL=9 N·m时传统超前角弱磁控制算法转速和d，q轴电流波形Fig.6 The waveforms of speed and d，q currents with traditional leading angle flux weakening control algorithm when TL=9 N·m

负载转矩TL=9 N·m，给定转速3 000 r/min，加速时间2 s时，图6和图7分别给出了采用传统超前角弱磁控制算法和本文提出的改进型超前角弱磁控制算法的实验结果。由两图对比可以看出，采用传统超前角弱磁控制算法在弱磁升速阶段，会出现d，q轴电流和速度的剧烈震荡(如图6中的虚线框所示)。采用改进型超前角弱磁控制算法之后，由于使用了SVPWM过调制控制策略，增强了逆变器的电压输出能力，弱磁升速阶段的电流和速度震荡明显减小，改善了系统的动态性能。

图7 TL=9 N·m时改进型的超前角弱磁控制算法转速和d，q轴电流波形Fig.7 The waveforms of speed and d，q currents with improved leading angle flux weakening control algorithm when TL=9 N·m

负载转矩TL=12 N·m，给定转速3 000 r/min，加速时间2 s时，图8给出了采用传统超前角弱磁控制算法的转速波形，可以看出随着负载的增大，弱磁阶段的稳态速度无法达到3 000 r/min，并且速度有震荡。图9给出了传统超前角弱磁控制算法在过调制基础上增大Umax后转速和d，q轴电流的波形，虽然稳态速度能够到达3 000 r/min，但是稳态阶段速度和d，q轴电流都有较大的震荡，稳态性能较差。采用本文提出的改进型超前角弱磁控制算法后转速和d，q轴电流的波形如图10所示，可以看出通过改进型超前角弱磁控制算法中的q轴电流误差闭环最终将弱磁阶段的电压调整到输出范围内，基本消除了速度稳态误差。与图9的对比可以看出，稳态阶段速度和d，q轴电流的波动很小，稳态性能得到了明显改善。

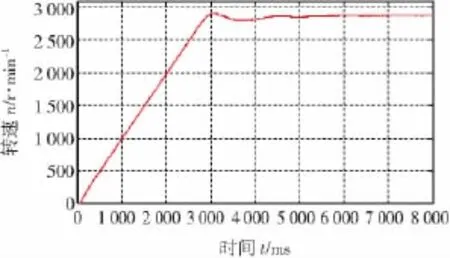
图8 TL=12 N·m时传统超前角弱磁控制算法转速波形Fig.8 The waveform of speed with traditional leading angle flux weakening control algorithm when TL=12 N·m

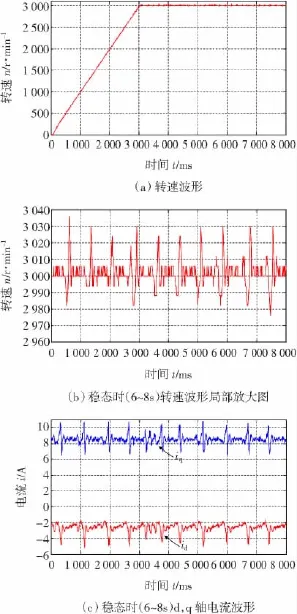
图9 TL=12 N·m时增大Umax后转速和d，q轴电流波形Fig.9 The waveforms of speed and d，q currents after increasing Umaxwhen TL=12 N·m

图10 TL=12 N·m时改进型超前角弱磁控制算法速度和d，q轴电流波形Fig.10 The waveforms of speed and d，q currents with improved leading angle flux weakening control algorithm when TL=12 N·m

5 结语

本文以表贴式永磁同步电机为研究对象，在传统超前角弱磁控制算法的基础上，针对电机在弱磁调速时，随着负载增加而出现的动态过程电流震荡变大，稳态时速度波动以及稳态误差变大的现象，分析其主要原因为逆变器的电压输出能力不足和弱磁调速时采用的电压闭环控制。为此，本文提出一种改进型超前角弱磁控制算法，具有如下特点:

1)采用了一种计算量小，便于实现的SVPWM过调制算法，提高了逆变器直流母线电压利用率，增强了电压输出能力，减小了速度响应动态过程的电流震荡，改善了弱磁调速的动态性能;

2)采用q轴电流误差闭环代替电压闭环进行弱磁控制，有效地减小了稳态阶段的速度波动，避免了稳态速度的下降，提高了系统的稳态性能和弱磁控制的鲁棒性。

［1］ CHEN G H，TSENG K J.Design of a permanent magnet directdriven wheel motor drive for electric vehicle［C］//1996 IEEE Conference of Power Electronics Specialists，June 23 －27，1996，Baveno，Italy.1996:1933 －1939.

［2］ BOSE B K.A high-performance inverter-fed drive system of an interior permanent magnet synchronous machine［J］.IEEE Transactions on Industry Applications，1988，24(6):987 －997.

［3］ MORIMOTO S，SANADA M，TAKEDA Y，et al.Wide-speed operation of interior permanent magnet synchronous motors with highperformance current regulator［J］.IEEE Transactions on Industry Applications，1994，30(4):920 －926.

［4］ SOZER Y，TORREY D A.Adaptive flux weakening control of permanent magnet synchronous motors［C］//The 1998 IEEE Industry Applications Conference，October 12 － 15，1998，St.Louis，USA.1998:475 －482.

［5］ CHEN Jiunnjiang，CHIN Kanping.Automatic flux-weakening control of permanent magnet synchronous motors using a reduced-order controller［J］.IEEE Transactions on Power Electronics，2000，15(5):881－890.

［6］ 唐朝晖，丁强，喻寿益，等.内埋式永磁同步电机的弱磁控制策略［J］.电机与控制学报，2010，14(5):68 －72.

TANG Zhaohui，DING Qiang，YU Shouyi，et al.Research of flux weakening strategy of interior permanent magnet synchronous motor［J］.Electric Machines and Control，2010，14(5):68 － 72.

［7］ 刘海燕，王毅，刘杰，等.电动车用感应电机弱磁控制研究［J］.电机与控制学报，2005，9(5):452－455.

LIU Haiyan，WANG Yi，LIU Jie，et al.Field-weakening control of induction motor for electric vehicles［J］.Electric Machines and Control，2005，9(5):452 －455.

［8］ BONHO B，PATEL N，SCHULZ S，et al.New field weakening technique for high saliency interior permanent magnet motor［C］//The 2003 IEEE Industry Applications Conference，October 12 －16，2003，Salt Lake City，USA.2003:898－905.

［9］ ZORDAN M，VAS P，RASHED M，et al.Field-weakening in vector controlled and DTC PMSM drive，a comparative analysis［C］//2000 8th International Conference on Power Electronics and Variable Speed Drives，September 18 － 19，2000，London，UK.2000:493－499.

［10］ 秦晓飞.永磁同步交流伺服驱动关键技术研究［D］.北京:中国科学院自动化研究所，2010.

［11］ 王旭东，张思艳，余腾伟.SVPWM过调制中控制角算法的分析与应用［J］.电机与控制学报，2010，14(12):63 －67.

WANG Xudong，ZHANG Siyan，YU Tengwei.Control angle algorithm of SVPWM over modulation analysis and application［J］.Electric Machines and Control，2010，14(12):63 －67.

［12］ HOLTZ J.Pulsewidth modulation a survey［J］.IEEE Transaction Industry Electron，1992，39(6):410 －420.

［13］ HOLTZ J.On continuous control of PWM inverters in the over modulation range including the six-step mode［J］.IEEE Transactions on Power Electronics，1993，8(4):546 －552.