永磁同步电机神经网络逆解耦控制研究
赵君, 刘卫国, 骆光照, 张文婧
(西北工业大学自动化学院,陕西西安710072)
0 引言
永磁同步电机(permanent magnet synchronous motor,PMSM)因具有体积小、运行可靠、能量转换效率高、调速范围广、动静态特性好等优点而被广泛应用于各种伺服控制系统中。解耦控制是实现PMSM高性能动静态特性的关键,目前常用的解耦控制方法有矢量控制、直接转矩控制、逆系统线性解耦控制等方法,但是大多数永磁同步电机控制方法需要依赖系统精确数学模型,因此在实际应用中具有一定的局限性。
神经网络及其改进方法等传统理论在系统建模方面已取得了较好的进展,它可以不考虑电机的部件特性,可以直接从系统整体上进行动态辨识,是一种较为可行的建模和辨识方方法,文献[1-4]是国内外学者将神经网络逆系统解耦控制理论在感应电机中应用的成果,基于神经网络的逆系统控制方法[5-6]克服了大多数控制方法依赖精确数学模型的缺点,可实现对一般非线性系统的线性化解耦控制,并且其结构简单、易于工程实现,文献[7-8]为工程上实现神经网络逆系统解耦控制提供了解决途径。神经网络逆系统解耦控制思路为,采用神经网络来构造原系统的“逆系统”,将对象补偿为具有线性传递关系及被解耦的一种规范化系统,在分别对各解耦子系统设计线性闭环控制器,从而实现对原线性耦合系统的高性能控制[9-14]。本文针对PMSM转速和定子电流之间的耦合特性,采用神经网络逆系统代替解析逆系统,将神经网络的非线性逼近能力与逆系统线性化解耦特点相结合,实现永磁同步电机的解耦控制,提高永磁同步电机的鲁棒性与动静态性能。
1 永磁同步电机模型及可逆性分析
为了便于分析PMSM同时便于证明系统可逆性,这里采用d-q轴数学模型,它不仅可以用于分析PMSM的稳态特性,也可以用于分析其瞬态特性。为建立PMSM的d-q轴模型,做如下假设:①忽略空间谐波,设三相绕组在空间上对称放置,所产生的磁动势沿气隙圆周呈正弦分布;②忽略电机铁心非线性饱和影响,认为绕组自感和互感恒定;③忽略铁心损耗;④不考虑频率和温度变化对绕组电阻的影响;⑤忽略转子的阻尼绕组[15-16]。
永磁同步电机在d-q轴坐标系下,电压方程模型可表述为

转矩方程为
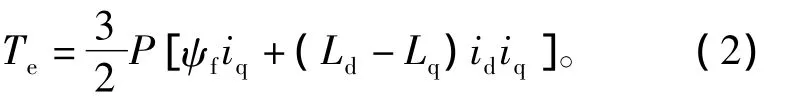
运动方程为

式(1)~式(3)中,ωr为电机电气速度,ω为电机机械角速度,且满足ωr=pω,p为微分算子;ud和uq分别为永磁同步电机d-q轴电压;id和iq分别为永磁同步电机d-q轴电流;R为绕组内阻;Ld和Lq为d-q轴电感;ψd和 ψq为 d-q轴磁链;ψf电机永磁体磁链;P为电机极对数;Te、TL、F和J分别为电机电磁转矩、负载转矩、摩擦系数和转子转动惯量。
可得,PMSM在d-q轴坐标系下的微分方程可以表述为
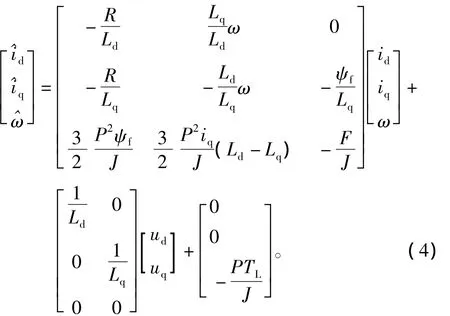

由以上推导可知,PMSM可以等价为一个两输入两输出的三阶非线性系统,对于该MIMO系统可以采用Interactor算法进行可逆性证明[15],通过对输出变量y求时间导数,直到在y的n阶导数中首次出现输入量u,则

可以看出对于输出变量y1,y′1首次包含输入变量u,则停止求导。令Y1=y′1,则Y1对输入u的雅可比矩阵可以表述为

继续对输出变量2求导可得
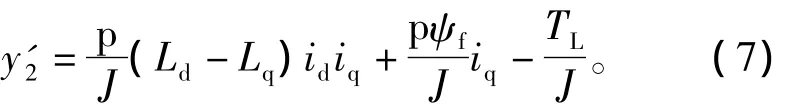
由式(7)可知y′2中不包含输入变量 u,因此继续对 y′2求导,可得

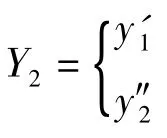
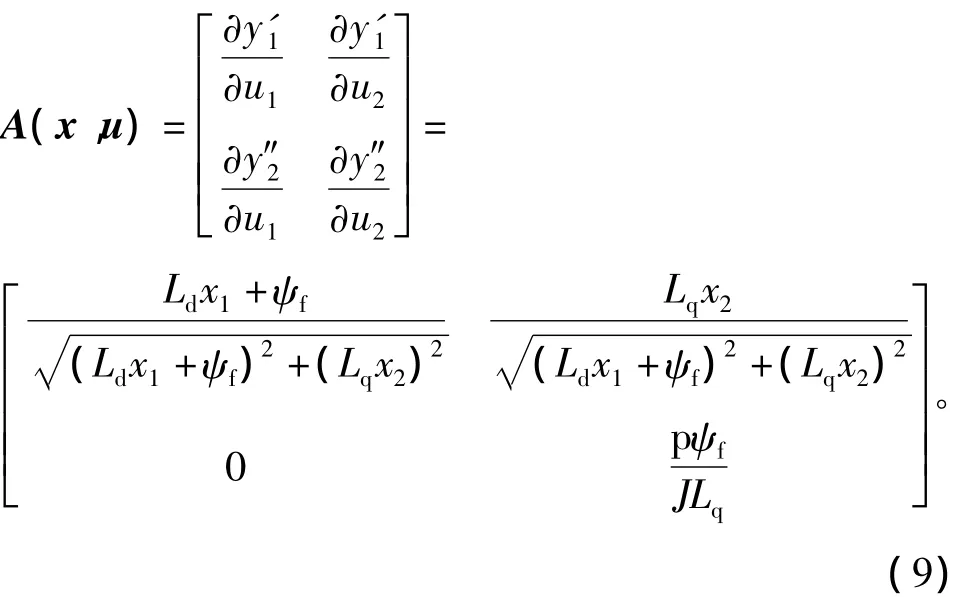
由式(9)可的其行列式的值为


令[ψ′sω″]=[υ1υ2],且由式(5)与式(8)解得永磁同步电机状态反馈系统的解析逆表达式为
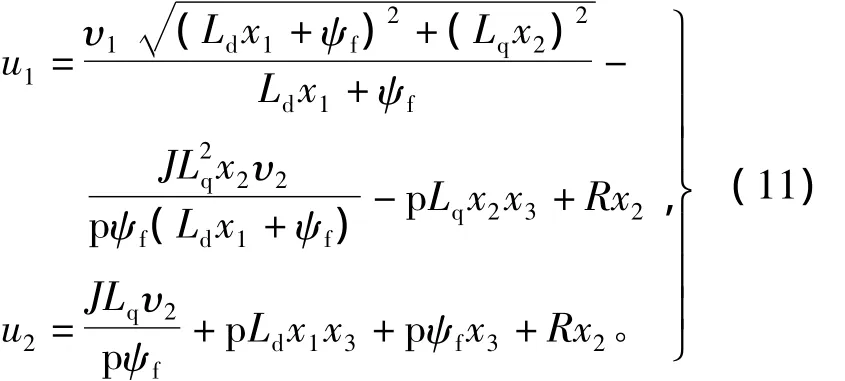
所以逆系统可以表示为
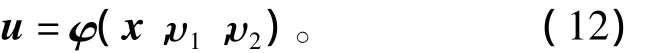
2 永磁同步电机神经网络逆系统解耦控制建模
2.1 PMSM逆系统模型
神经网络逆系统解耦,通常采用由静态神经网络和若干积分器组成的动态神经网络构造连续系统的逆系统[17-20],并对被控系统进行线性化与解耦。由以上分析可知,永磁同步电机的数学模型具有可逆性,且具有完备的相对阶,因此选择输入积分实现方式对永磁同步电机进行解耦控制。将逆系统与永磁同步电机系统复合成两个伪线性系统,如图1所示,包括具有二阶积分关系的转速子系统与具有一阶线性积分关系的磁链子系统,因此实现了系统输入输出线性化解耦[15]。

图1 PMSM神经网络逆系统结构Fig.1 Control structure of PMSM based on ANN inverse system
2.2 PMSM逆系统神经网络结构
在神经网络逆系统控制结构中,使用静态神经网用于非线性映射的逼近。本文采用了BP神经网进行非线性逼近,该神经网络包括一个输入层、一个隐含层和一个输出层。由于PMSM在d-q坐标系下的数学模型为三阶系统,因此输入层控制量为{usd,usq},输出层变量为{ψs,ω}。本文静态神经网络隐层神经元选用tansig函数,则第i个隐层神经元的输出可以表述为

其中n为隐层神经元个数。根据Kolmogorov定理,本文选取隐层神经元个数为12,输出层函数选取purelin纯线性传递函数,可知该三层神经网络可以逼近任意精度的非线性映射。为提高神经网络的泛化能力,将输入输出变量信号进行归一化处理,使输出输出信号具有相同的数值范围,本文所采用的归一化原则为

图2为本文构造出的神经网络结构。

图2 三层BP神经网络结构Fig.2 Radical structure of BP network
2.3 PMSM逆系统神经网络建模
PMSM逆系统神经网络结构中的输入变量为{ψs,ψ′s,ω,ω′,ω″}及两个输出变量{usd,usq},本文的训练数据由解析逆解耦控制通过dSPACE半物理仿真平台统获得。
为保证模型具有较强的泛化能力,磁链与转速输入给定应为正太分布的随机量,且仿真过程对于每一个磁链与转速的参数组合仿真持续时间为3 s,采样频率200 Hz,以保证数据中包含足够的稳态与瞬态信息,然后对样本进行归一化处理,选取其中的2/3的数据作为训练样本集,剩余数据作为检验样本集,用于检验模型的泛化能力。
本文采用图2中设计的神经网结构,采用BP算法对网络进行训练,离线训练736步后,网络输出均方根误差达到目标值1×10-5,使用检验样本集数据对训练好的神经网络进行检验,输出预测精度良好。但是,由于BP神经网存在陷入局部极小,初值选取与隐层节点个数选取等问题,本文在采用其他参数和网络结构进行离线训练时,出现了模型泛化能力差或训练不收敛现象,针对此类问题的解决方法,本文不进行深入分析。
本文实现了PMSM神经网络三阶逆模型构造,由于神经网络逆和PMSM模型构成的伪线性系统的开环控制效果是不理想的,因此本文采用PID控制器对该伪线性系统进行闭环控制,控制原理如图3所示。
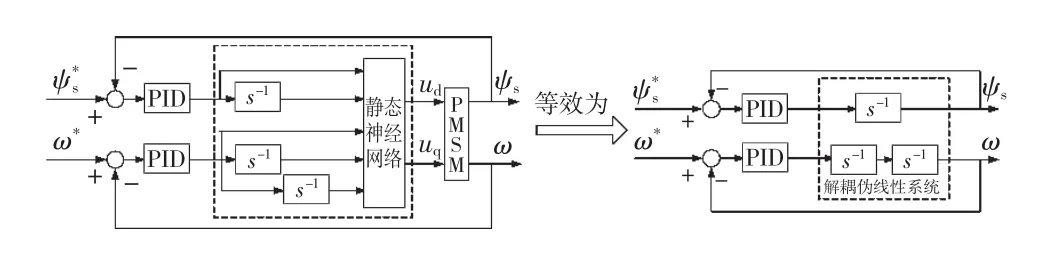
图3 PMSM神经网络逆解耦控制系统框图Fig.3 Control diagram of PMSM based on ANN inverse system algorithm
3 半物理仿真试验
本文仿真试验通过构建dSPACE半物理仿真平台实现,该仿真平台分为3部分:dSPACE半物理仿真实验系统、参数测量实验系统、外围传感器及测试设备,可以实现与Matlab/SIMULINK的无缝连接,将基于SIMULINK的图形化实时控制模型直接编译、下载到目标控制器,实现控制器的快速原型设计。同时,借助Control desk及MLIB/MTRACE等实验软件,编辑可视化操作界面,实现数据实时、准确捕获、存储及在线处理。本文构建的试验系统如图4所示。系统采用矢量控制方法实现PMSM控制,采用磁链观测电流模型[21]基于dSPACE系统完成磁链观测,实验过程参数显示通过Control desk图形界面完成显示功能。
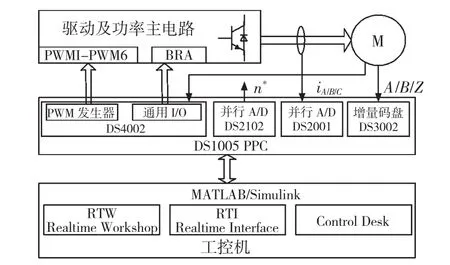
图4 dSPACE半物理仿真平台Fig.4 dSPACE simulation platform of PMSM
利用图4建立的dSPACE半物理仿真平台进行实验,PMSM参数为:额定功率PN=0.75 kW,额定转速2 000 r/min,极对数P=4,静态测量电感、电阻参数为 Ld=Lq=9.8 mH,R=1.47 Ω。首先,对PMSM的解析逆控制与神经网络逆系统解耦控制进行对比实验。实验中永磁同步电机工作在额定参数下,转速给定阶跃变化,利用Magtrol加载台为系统提供负载转矩,磁链给定0.7 Wb,负载转矩恒定为1 N·m,PMSM转速与定子磁链曲线如图5所示,磁链给定阶跃变化,转速给定1 200 r/min,负载转矩恒定为1 N·m,PMSM转速与定子磁链曲线如图6所示。
由图5可以看出,负载恒定转速变化时,解析逆控制与神经网逆控制方法均可以保证系统磁链输出稳定,可以说明采用解析逆控制与神经网络逆系统解耦控制的系统动态特性基本一致。
为进一步证明神经网络逆控制方法的有效性,将系统磁链与转速给定同时变化,在系统转速反馈为1 200 r/min,磁链反馈为0.35 Wb稳定运行5 min后,通过Dspace的Control desk将转速与磁链给定设置为250 r/min与0.85 Wb,图6为该实验波形。实验结果表明,在动态过程中转速与磁链反馈出现了超调,稳态过程磁链和转速达到了控制要求,调节时间小于800 ms,因此证明神经网络逆系统解耦控制方法可以满足大多数PMSM控制领域应用。
为验证神经网络逆系统解耦控制对负载扰动的鲁棒性,图7给出了负载变化时定子磁链和转速响应的实验曲线。给定转速(1 200 r/min)与磁链(0.45 Wb),当负载由0.3 N·m突变到1 N·m,采用神经网络逆系统解耦控制方法,系统转速曲线存在小范围调整,定子磁链受到的影响较小。
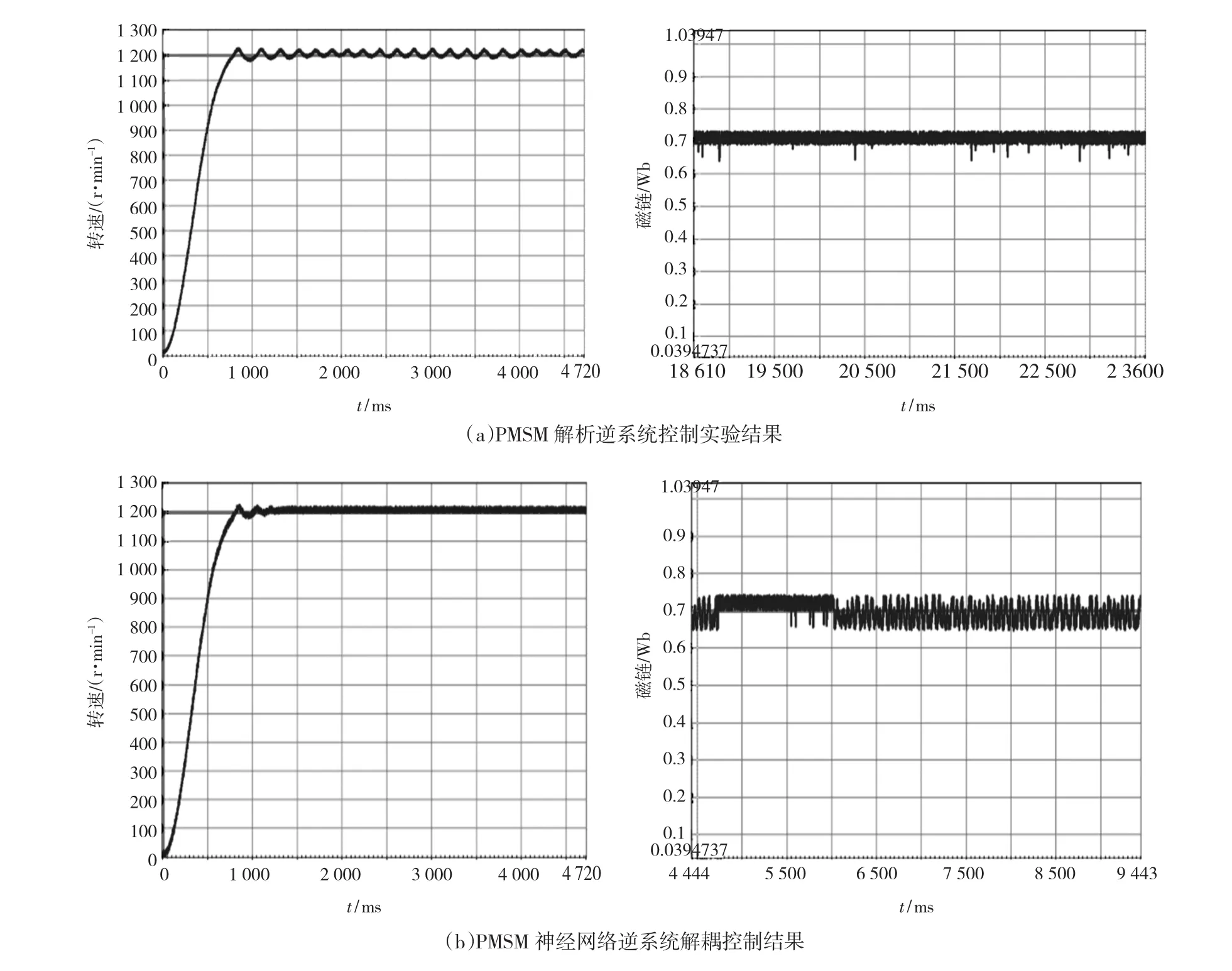
图5 恒磁链解耦控制特性比较Fig.5 Performance of decoupling control with constant magnetic flux linkage

图6 解耦控制特性Fig.6 Performance of decoupling control
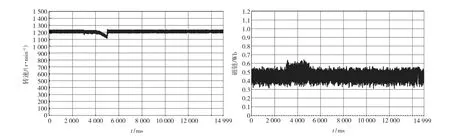
图7 负载突变系统解耦控制特性Fig.7 Performance of decoupling control with load variation
4 结语
本文基于dSPACE系统构建半物理仿真平台,将神经网络逆系统解耦控制方法应用于PMSM解耦控制中,将具有多变量、强耦合、非线性特点的PMSM,动态解耦成二阶线性转速子系统和一阶线性定子磁链子系统,采用传统的PID控制器对两个伪线性子系统进行闭环控制,实现了转速和定子磁链的动态解耦,实验结构表明系统具有良好的动、静态特性。在负载突变及周期性变化的工况下,系统的转速与磁链仍具有较好的鲁棒性与稳定性,证明神经网络逆系统解耦控制用于非线性系统是可行的,为永磁同步电机的解耦控制提供了一种新途径。
[1] MARINO P,MILANO M,VASCA F.Linear quadratic state feedback and robust neural network estimator for field-oriented-controlled induction motors[J].IEEE Transactions on Industrial Electronic,1999,46(1):150 -161.
[2] DAI X,HE D,ZHANG X,et al.MIMO system invertibility and decoupling control strategies based on ANNαth-order inversion[J].IEE Proceedings-Control Theory Applications,2001,148(2):125-136.
[3] 张兴华,戴先中.基于逆系统方法的感应电机调速控制系统[J].控制与决策,2000,15(6):708 -711.
ZHANG Xinghua,DAI Xianzhong.Speed control system of induction motor based on inverse system method[J].Control and Decision,2000,15(6):708 -711.
[4] BRDYS M A,KULAWSK G J.Dynamic neural controllers for induction motor[J].IEEE Transactions on Neural Networks,1999,10(2):340-355.
[5] 戴先中,刘军,冯纯伯.连续非线性系统的神经网络α阶逆系统控制方法[J].自动化学报,1998,24(4):463-468.
DAI Xianzhong,LIU Jun,FENG Chunbo.Neural network αth -order inverse system control method for nonlinear continuous system[J].Acta Automatica Sinica,1998,24(4):463 -468.
[6] 戴先中,张兴华,刘国海.感应电机的神经网络逆系统线性化解耦控制[J].中国电机工程学报,2004,24(1):112-117.
DAI Xianzhong,ZHANG Xinghua,LIU Guohai.Decouping control of induction motor based on neural networks inverse[J].Proceedings of the CSEE,2004,24(1):112 -117.
[7] HUANG Changchiun,TANG Tsanntay.Spinline tension control in melt spinning by discrete adaptive sliding-mode controllers[J].Journal of Applied Polymer Science,2006,100(5):3816-3821.
[8] CHE Yanbo,SHA Lin,CHENG K W E.Variable gain intelligent control of multi-motor synchronizations system[C]//2nd International Conference on Power Electronics Systems and Applications,November 14-16,2006,Hong Kong,China.2006:68-72.
[9] BOUAFIA A,GAUBERT JP,KRIM F.Analysis and design of new switching table for direct power control of three-phase PWM rectifier[J].IEEE Transactions on Industry Electronics,2008,78(1):703-709.
[10] BAKTASH A,VAHEDI A,MASOUM M A S.Improved switching table for direct power control of three-phase PWM rectifier[J].IEEE Transactions on Industry Electronics,2008,78(1):1-5.
[11] WOON K N,BEI G.Feedback-linearization-based nonlinear control for PEM fuel cells[J].IEEE Transactions on Energy Conversion,2008,23(1):179 -189.
[12] 刘贤兴,卜言柱,胡育文,等.基于精确线性化解耦的永磁同步电机空间矢量调制系统[J].中国电机工程学报,2007,27(30):54-59.
LIU Xianxing,BU Yanzhu,HU Yuwen,et al.Space vector modulation system for permanent magnet synchronous motor based on precision linearization decoupling[J].Proceedings of the CSEE,2007,27(30):54-59.
[13] 孟昭军,孙昌志,安跃军.基于时间延迟状态反馈精确线性化的PMSM混沌反控制[J].电工技术学报,2007,22(3):27-31.
MENG Zhaojun,SUN Changzhi,AN Yuejun.Chaos anti-control of permanent magnet synchronous motor based on exact linearization via time-delayed state variable feedback[J].Transactions of China Electrotechnical Society,2007,22(3):27 -31.
[14] 郭家虎,张鲁华,蔡旭.双馈风力发电机的精确线性化解耦控制[J].电机与控制学报,2009,13(1):57 -62.
GUO Jiahu,ZHANG Luhua,CAI Xu.Exact linearization control scheme of DFIG[J].Electric Machines and Control,2009,13(1):57-62.
[15] 戴先中.多变量非线性系统的神经网络逆控制方法[M].北京:科学出版社,2005:1-159.
[16] 周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社,2005:1-137.
[17] 石峰,查晓明.应用微分几何理论的三相并联型有源电力滤波器解耦控制[J].中国电机工程学报,2008,28(15):92 -97.
SHI Feng,ZHA Xiaoming.Decoupled control of the shunt threephase active power filter applying differential geometry theory[J].Proceedings of the CSEE,2008,28(15):92 -97.
[18] 刘贤兴,胡育文.永磁同步电机的神经网络逆动态解耦控制[J].中国电机工程学报,2007,27(27):72 -76.
LIU Xianxing,HU Yuwen.Dynamic decoupling control of PMSM based on neural network inverse method[J].Proceedings of the CSEE,2007,27(27):72-76.
[19] LIN Faajeng,SU Homing.A high-performance induction motor drive with on-line rotor time - constant estimation[J].IEEE Transactions on Energy Conversion,1997,12(4):297 -303.
[20] TAJIMA Hirokazu,GUIDI Giuseppe,UMIDA Hidetoshi.Consideration about problems and solutions of speed estimation method and parameter tuning for speed-sensorless vector control of induction motor drives[J].IEEE Transactions on Industry Applications,2002,38(5):1282 -1289.
[21] BOSE B K.现代电力电子学与交流传动[M].北京:机械工业出版社,2005:270 -350.

