四维超混沌系统及其在信号加密中的应用
于春雨, 朱建良, 郭建英
(1.哈尔滨理工大学测控技术与通信工程学院,黑龙江哈尔滨150080;2.哈尔滨理工大学电气与电子工程学院,黑龙江哈尔滨150080)
0 引言
自第一个超混沌系统诞生以来,由于其更强的随机性和不可预测性,其理论研究与硬件实现及其在混沌保密通信等一些非传统的工程技术领域的应用成为非线性电路理论与系统的前沿课题。尤其是多维混沌的理论设计及其电路实现等问题备受人们的关注[1-3],对此,国内外学者做了深入的分析和研究[4-5]。Liao[6]、Feki[7]、Cuomo[8]、Dudieu[9]等人分别对基于混沌的信号加密与安全通信做了研究。但是,将超混沌系统应用于保密通信的研究还是少之又少[10-11]。
本文提出了一个四维超混沌系统,并设计了相应的实现电路,系统的Matlab仿真结果与所设计电路的Multisim仿真结果完全一致;该系统不仅为混沌加密通信提供了新的信号源,而且可用新的混沌信号源实现信号加密,同时将迭代次数与混沌信号的加减手段相结合来设置密码。研究结果表明,该方法不仅可以实现对信号进行加密,且与其它加密方法相比较,该方法具有良好的保密性,这一方法只有在多维混沌系统中才能实现。
1 四维超混沌系统模型
构建的四维超混沌系统为
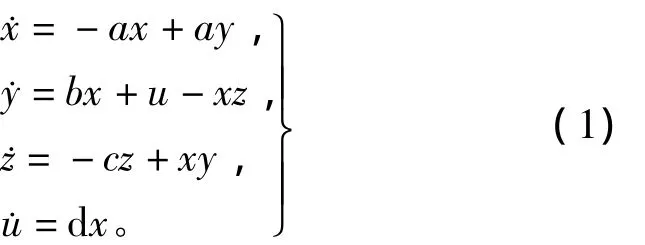
式中:a=25;b=35;c=3;d=-8。
对系统(1)进行 Lyapunov指数分析,如图1所示。
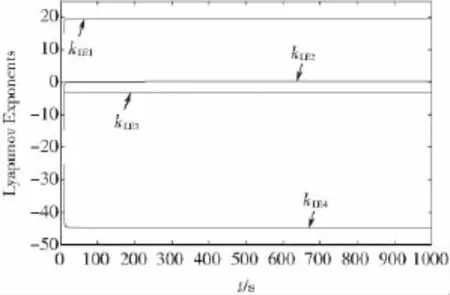
图1 Lyapunov指数Fig.1 Lyapunov Exponents(LE)
图中:kLE1=19.452 1,kLE2=0.228 581,kLE3=-3,kLE4= -44.680 4。
系统(1)的所有Lyapunov指数和为负,且有两个Lyapunov指数为正。因此,所构建的系统为超混沌系统。
对于系统(1),由于散度
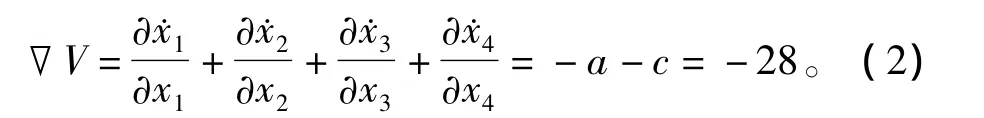
所以,包含系统轨线的每个体积元均以指数率e-28t收敛。所有系统的轨线最终会被限制在一个体积为0的极限点集上,并且它的渐近动力学行为会被固定在一个吸引子上,这说明了混沌吸引子的存在性。由Matlab仿真得到的吸引子如图2所示。
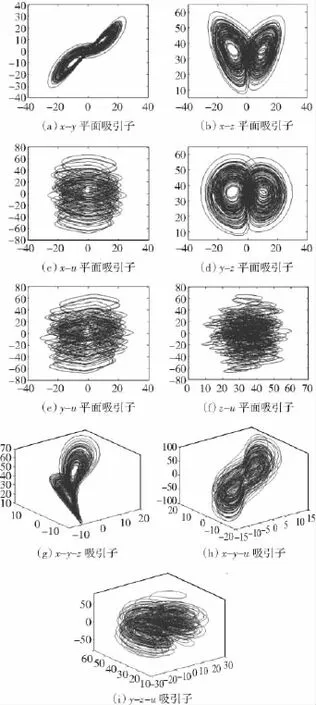
图2 系统(1)的相轨迹图Fig.2 Hyperchaotic attactors of System(1)
2 系统的电路实现
为了验证系统(1)的超混沌行为,设计了实现该四维超混沌系统的电路如图3所示。该混沌电路主要由3个部分构成:集成运算放大器,模拟乘法器,线性电阻、电容。其中,集成运算放大器采用LF353芯片,用来实现电路加减运算和积分运算;模拟乘法器采用AD633芯片,用来实现系统(1)的非线性项。电路的输出电压分别对应系统(1)中的x,y,z,u。
电路的Multisim仿真得到的相轨迹如图4所示。与Matlab仿真结果完全一致。

图3 四维超混沌系统的实现电路Fig.3 Circuit for Realizing Hyperchaotic System(1)

图4 系统(1)实现电路的相轨迹图Fig.4 Hyperchaotic attactors of System(1)
3 四维超混沌系统在信号加密中的应用
对于信号的加密采用的是混沌隐藏技术,用此技术可以传递模拟和数字信息,其思想是以混沌同步为基础,利用混沌信号的伪随机性,把混沌信号叠加到被加密的信号上,即把要加密的信号隐藏在混沌信号中,实现对原有信号进行混沌加密[12-15]。若需还原原信号,则接收端的混沌信号解调装置必须与发射端相同步。以此达到保密通信的目的。本文综合运用多次迭代及混沌信号相加减的方法对原始方波信号进行混沌隐藏加密,如图5(a)所示。
在信息传递的过程中,为确保原信号不被第三方察觉,发送方与接收方可事先约定把混沌信号的相加减和迭代次数设定为密码,更有利于保密。如图5(b)所示。被加密的方波信号经过了5次迭代加密,且迭代次数越多,加密效果越好,越不易被破解,即确保了信息传递的安全性。解密信号就是加密信号的逆过程,必须知道原混沌源以及加密的相加减的方法和迭代次数,否则将无法解密出原有的信号,如图6所示。

图5 待加密方波信号的仿真模型Fig.5 Simulation Model of Square Wave Signal to be Encrypted

图6 方波信号的加密与解密仿真Fig.6 Simulation of Square Wave Signal to be Encrypted and Decrypted
4 结论
本文构造了一个新的四维超混沌系统,通过Lyapunov指数分析和计算机仿真,得出如下结论:
1)Lyapunov指数分析证明了该系统具有超混沌特性。
2)系统的Matlab仿真结果与相应的实现电路的Multisim仿真结果完全一致,证明了该系统的可实现性。
3)为混沌加密通信提供了新的信号源,利用该四维超混沌系统对信号进行加密研究,通过对混沌信号的相加减和迭代次数设置密码,增加了解密难度,进一步说明了该系统的实用性。
4)所设计的电路结构简单,成本低廉,调试容易,便于实现。
另外随着混沌研究的不断深入,构造出新的更高维数的混沌吸引子并实现其技术应用,将为混沌研究开辟出新的思路,也将为信息加密提供更加宽广的应用前景。
[1] Lü J,Yu S M,Leung H,Chen G.Experimental verification of multi-directional multi-scroll chaotic attractors[J].IEEE Transactions on Circuits and Systems I,2006,53(1):149 -165.
[2] Yu S M,Lü J,Leung H,Chen G.Design and implementation of n-scroll chaotic attractors from a general Jerk circuit[J].IEEE Transactions on Circuits and Systems,2005,52(7):1459 -1476.
[3] Lü J,Chen G,Yu X H,Leung H.Design and analysis of multiscroll chaotic attractors from saturated function series[J].IEEE Transactions on Circuits and Systems I,2004,51(12):2476-2490.
[4] 王光义,丘水生,许志益.一个新的三维二次混沌吸系统及其电路实现[J].物理学报,2006,55(7):3295-3301.
WANG Guangyi,QIU Shuisheng,XU Zhiyi.A new three-dimensional quadratic chaotic system and its circuitry implementation[J].Acta Physica Sinica,2006,55(7):3295 -3301.
[5] 王繁珍,齐国元,陈增强,等.一个四翼混沌吸引子[J].物理学报,2007,56(6):3137 -3144.
WANG Fanzhen,QI Guoyuan,CHEN Zengqiang,et al.On a four-winged chaotic attractor[J].Acta Physica Sinica,2007,56(6):3137-3144.
[6] LIAO T L,TSAISH.Adaptive synchronization of chaotic systems and its application to secure communications[J].Choas Solitons& Fractals,2000,9(11):1387 -1396.
[7] FEKIM.An adaptive chaos synchronization scheme applied to secure communication [J].Chaos,Solitons & Fractals,2003,18(1)141-148.
[8] CUOMO K M,OPPENHEIM A V,STROGATZ S H.Synchronization of lorenzed2based chaotic circuits with applications to communication [J].IEEE Transactions on Circuits and Systems,1993,40(10):634-642.
[9] DUDIEU H,KENNEDY M P,HASLER M.Chaos shift keying:modulation and demodulation of a chaotic carrier using self-synchronizing chua.s circuit[J].IEEE Transactions on Circuits and Systems,1993,40(10):634 -642.
[10] 申敏,刘娟.一个新超混沌系统及其EWB电路仿真[J].重庆邮电大学学报:自然科学版,2010,22(1):71-74.
SHEN Min,LIU Juan.A new hyperchaotic system and its circuit simulation by electronic workbench[J].Journal of Chongqing U-niversity of Posts and Telecommunications:Natural Science Edition,2010,22(1):71 -74.
[11] 胡汉平,卢鹏宇,王祖喜,等.数模混合混沌系统的设计与电路仿真[J].华中科技大学学报:自然科学版,2007,35(10):8-11.
HU Hanping,LU Pengyu,WANG Zuxi,et al.Design and circuits simulation of mixed digital-analog chaotic system[J].Journal Huazhong University of Science and Technology:Nature Science Edition,2007,35(10):8 -11.
[12] 尹元昭.一个通过混沌同步实现保密通信的新方法[J].电子与信息学报,2001,23(4):408 -412.
YIN Yuanzhao.A new way to secure communication via chaotic synchronization[J].Journal of Electronics and Information Technology,2001,23(4):408 -412.
[13] 孙克辉.混沌同步控制理论及其在信息加密中的应用研究[D].中南大学信息科学与工程学院,2005.
[14] 朱建良,孙鸣,朱博.基于四维混沌系统的图像加密研究[J].信息技术,2010(10):74-76.
ZHU Jianliang,SUN Ming,ZHU Bo.Four-dimensional chaotic system based image encryption algorithm[J].Information Technology,2010(10):74 -76.
[15] 徐江峰,杨有,黄小粟.基于广义同步混沌的图像加密方案[J].计算机工程,2006,32(6):154-156.
XU Jiangfeng,YANG You,HUANG Xiaosu.An image encryption algorithm based on generalized synchronization chaotic systems[J].Computer Engineering,2006,32(6):154 -156.

