双馈风力发电机三维温度场耦合计算与分析
丁树业, 葛云中, 陈卫杰, 徐殿国, 苗立杰
(1.哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001;2.哈尔滨电站设备集团公司,黑龙江哈尔滨150040;3.哈尔滨理工大学电气与电子工程学院,黑龙江哈尔滨150080;4.中国人民解放军96215部队,广西柳州545616)
0 引言
我国风能资源十分丰富,地面的风能总量约有16亿千瓦,其中近地面可供开发利用的约占16%,为2.53亿千瓦[1]。在风能利用方面,我国至2010年国内风电装机容量达到3 000万千瓦,占国内总装机容量的2.8%左右。目前,国内风力发电机的开发生产品种繁多[2],单机容量不断增大,2~3.0 MW以上的风电机组已经商业化,5 MW的风电机组也已经投入试运行,开始由陆地向海上和高海拔地区发展[3-4]。
随着风力发电机单机容量的日益增大,使得电机运行时产生的单位体积损耗显著增加,引起电机各部分温度升高,直接影响电机的寿命和运行的可靠性。因此,在发电机的运行过程中,必须采用相应的冷却介质有效地带走电机内的热量,使得发电机长期、可靠地运行。然而,发电机的通风结构以及冷却介质在电机内的分布特性均比较复杂,因此对发电机内温度场、温度分布特性进行有效地分析,对发电机稳定运行以及更大容量的发电机的设计均具有重要意义。
为了准确的对电机内温度场进行研究,国内外专家学者提出了许多计算方法[5],其中数值计算方法精度较高。目前运用数值计算的方法对不同种类电机内温度场[6-10]、不同工况下铁心与绕组间的热量传递[11]、转子通风方式和电机风量分配对电机温升的影响进行了诸多研究[12-13],为电机内的物理场的计算奠定了一定的基础。上述文献多是对电机的局部区域或相关因素对电机温度场的影响情况进行研究,本文在此基础上,对电机周向1/8区域内定子、转子以及流体区域的三维温度场进行研究,避免了对气隙和转子通风沟流量分配。
本文以一台1.5 MW风力发电机为例,采用有限体积元法对电机内流体场和温度场进行计算,得出内冷却介质在电机内流量分布规律和特性,并对电机三维温度场进行研究,分析电机温升分布规律和传热特性;最后将耦合计算结果与实测结果进行比较分析。
1 数学模型
电机冷却系统内流体流动与传热满足质量守恒定律、动量守恒定律、能量守恒定律。如果流动处于紊流状态,还要遵守附加的湍流运动方程,其守恒定律可以采用相应的控制方程进行描述[14-16]。
1.1 控制方程
根据流体力学理论,采用标准k-ε方程模型对流体进行描述。当流体为不可压缩且处于稳定流动状态时,采用通用控制方程[17]为
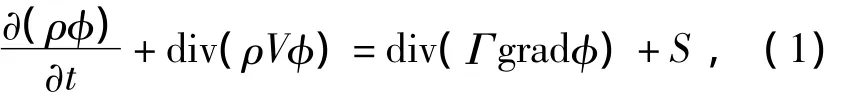
式中:φ、V为通用变量;ρ为流体密度,kg/m3;Γ 为扩展系数;S为源项。
1.2 三维热传导方程
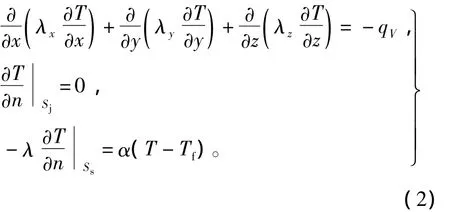
针对各向异性材料,由传热学基本原理可以写出求解域内稳态温度场基本方程及其边界条件为式中:T 为固体待求温度,℃;λx、λy、λz为求解域内各种材料沿x、y以及z方向的导热系数,W/(m·K);qV为求解域内各体热源密度之和,W/m3;α为散热表面的散热系数,W/(m2·K);Tf为散热面周围流体的温度,℃;Sj、Ss分别为绝热和散热面。
1.3 能量守恒方程
能量守恒定律是含热交换过程的流动系统须满足的基本定律,流体能量守恒方程为
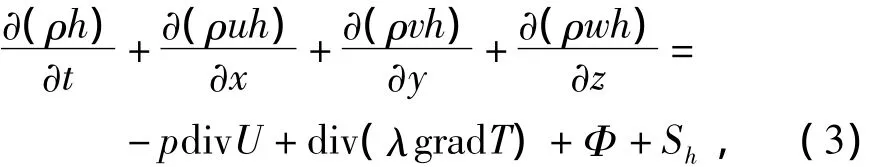
式中:U为流体的速度矢量;u、v、w分别为流体的速度分量;h为流体的比焓;T为流体温度;λ为流体的导热系数;p为流体压力;Sh为流体的内热源;Φ为由于粘性作用机械能转化为热能的部分,称为耗散函数。
2 求解模型确定
2.1 电机基本数据及冷却系统结构
本文以1.5 MW双馈风力发电机为例进行研究,电机基本参数:额定电压为620 V;额定电流为1192 A;额定功率为1.5 MW;额定转速为1 800 r/min;功率因数为0.85;频率为50 Hz。
该发电机采用的是双介质冷却方式,分为内外两路冷却。
1)内冷却系统,即风力发电机内部设置风扇,空气由设在电机端部的风扇强迫通风实现封闭式冷却,电机内通风系统结构如图1所示。
2)外冷却系统,发电机机壳内设有水循环系统,冷却水经过与一次冷却的热空气进行能量传递,将发电机运行因损耗而产生的热量带到外部。
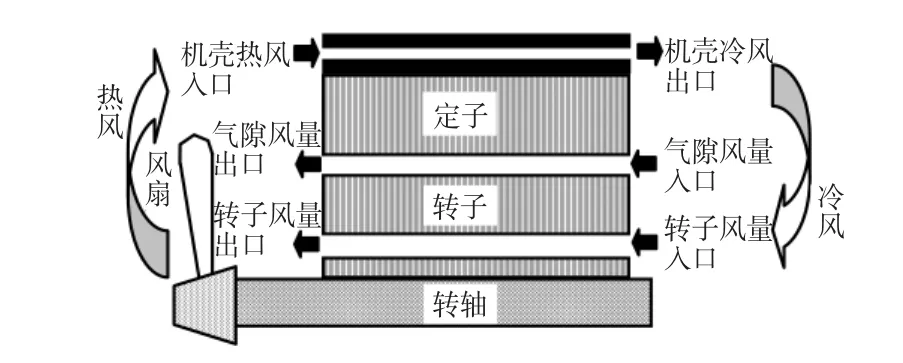
图1 发电机通风结构Fig.1 Ventilation structure of generator
2.2 假定条件
根据电机结构及电机内流体特性,作如下假设[9-13]:
1)电机内流场中,流体流速远小于声速,即马赫数(Ma数)很小,故把流体作为不可压缩流体处理。
2)由于电机中流体的雷诺数很大(Re>2 300),属于紊流,因此采用紊流模型对电机内流场进行求解。
3)由于电机结构周向的对称性,认为定、转子槽中心面和定、转子齿中心面是绝热的。
4)本电机转子采用隐极结构,转子表面光滑,不考虑电机旋转。
2.3 求解模型的确定
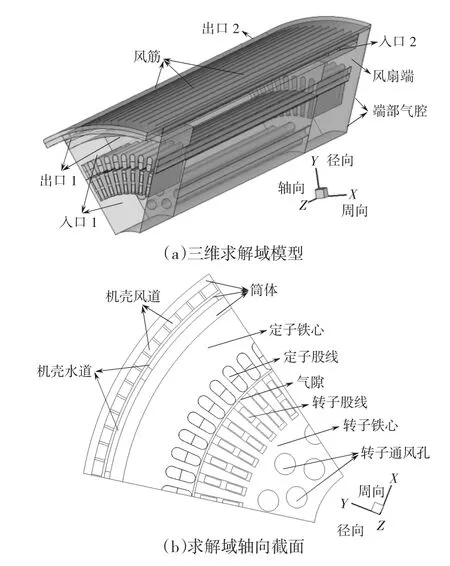
图2 求解域物理模型Fig.2 Physical model of solved region
2.3.1 求解域模型
考虑电机在圆周上几何结构周期性分布以及流体流动和传热特点,并依据基本假设,取电机周向1/8区域为研究对象,求解域物理模型如图2所示,发电机各部位的名称在图中均已标出,图中x轴表示定子周向方向,y轴表示定子径向方向,z轴表示定子轴向方向。
2.3.2 网格生成
对模型进行网格划分,采用四面体和六面体混合网格,检查网格质量,输出模型数据文件,求解域剖分如图3所示。

图3 求解域剖分图Fig.3 Subdivision map of solved region
2.3.3 边界条件的设置
流体场及温度场耦合求解的边界条件为:
1)环境温度为27℃(300 K),入口1为空气入口,入口2为水入口,两入口均给定为速度入口边界,根据给定的质量流量数值,可求得入口速度。
2)出口1为空气出口,出口2为水出口,均给定为压力出口边界条件,压力均为1个标准大气压。
3)发电机机壳外圆及转子内圆为散热面,给定散热系数和周围的空气温度:散热系数参考一般空冷电机设计经验给出[18],求解域两侧径向截面,设为周期性边界,其余与固体的接触的面均视为无滑移边界。
4)电机热源密度分布(W/m3):定子股线为226 416;定子铁心为38 451;转子股线为313 747;转子铁心80 726。
3 内冷却系统流变特性分析
由于发电机内热性能的分布特性完全由冷却介质的分布性能决定,首先对发电机内流体场进行分析。图4给出了该发电机三维求解域内空气速度分布。
通过对图4流体速度分布以及计算数值结果分析,可知:
空气入口截面较大,入流速度较低,冷空气绕过非风扇端的端部绕组进入转子通风孔和气隙中;在电机中空气沿轴向流过转子通风孔和气隙,由于气隙入口狭长表面积较小,空气流动入口风阻大,能量损失严重,空气在气隙中最大速度为21.22 m/s,风量占空气总流量的10.43%;空气在流入转子通风孔时空气的流动阻力系数相对较小,空气入口面积大,风阻较小,空气在转子通风孔的最大速度为49.85 m/s,风量占空气总流量的89.57%;当空气到达风扇端区域,空间变大,空气的速度降低,风速沿轴向截面的位置不同而不同,最高速度为43.26 m/s;在电机机壳风筋之间的风道中平均速度为32.52 m/s,空气流经一个循环,从求解域出口流出。
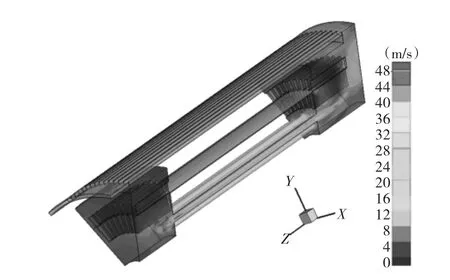
图4 空气速度分布图Fig.4 Velocity distribution of air
4 电机温度场特性分析
4.1 电机温度场分布
图5为电机额定运行时温升分布图,图6为定、转子槽中心截面和齿中心截面温升分布云图。

图5 电机温升分布图Fig.5 Temperature distribution of generator

图6 电机径向不同截面温升分布云图Fig.6 Temperature distribution of generator at different section
结合图5、图6可以得出,电机内最大温升分布在转子铁心段内的转子股线上,最大值为74.3 K;定子股线在风扇端温升较高,铁心段内温升较低,并沿轴向产生一定的变化规律,定子股线的最高温升为64.6 K;转子股线的热密度远大于转子铁心的热密度,两者之间紧密接触,转子股线以传导的方式将热量传导给转子铁心,转子齿部温升较大,最大值为62.0 K;定子铁心传热条件好,能够及时的把定子股线和铁心产生的能量传导给机壳,因而温升较低,最高温升为26.5 K。
4.2 定、转子股线沿轴向长度温升分布
为详细分析股线温升的分布规律,分别给出定、转子股线沿轴向长度的分布,如图7和图8所示。
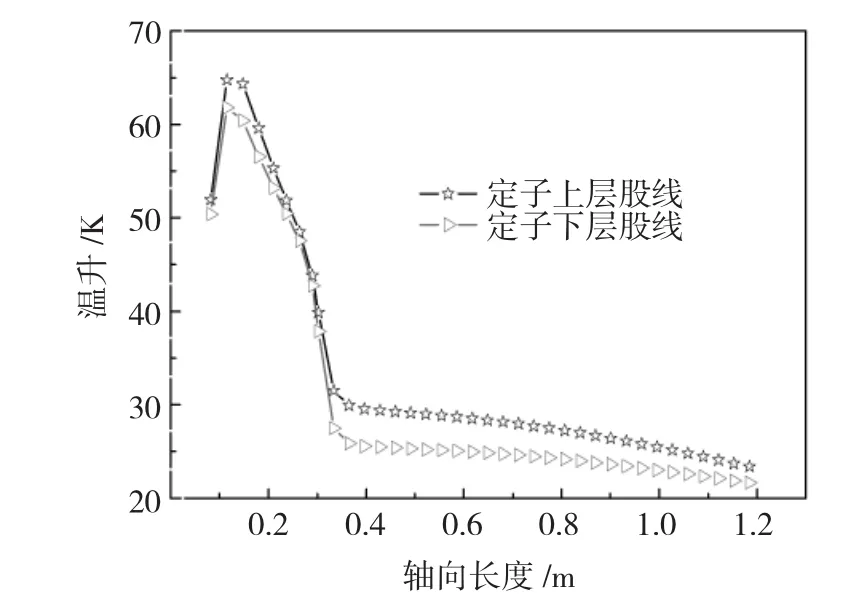
图7 定子股线沿轴向长度温升分布Fig.7 Temperature distribution of stator along with the axial length
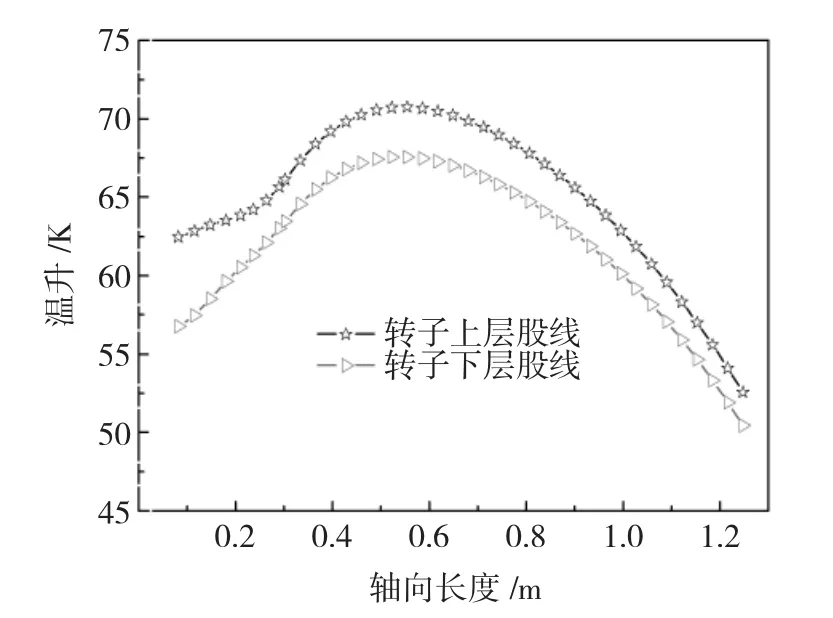
图8 转子股线沿轴向长度温升分布Fig.8 Temperature distribution of generator rotor along with the axial length
定子股线沿轴向长度温升变化规律为:定子上层股线温升高于下层股线温升;最高温升出现在风扇端,距离铁心一定距离处,最大值为64.6 K;最低温升分布在铁心段的进风端。在定子铁心段中股线温升沿轴向长度变化趋势基本一致,呈线性分布,由进风端至出风端温升变化逐渐增大,相差约2~5 K,在铁心段出风端温升略有上升。在端部气腔中股线温升急剧上升并达到最大值,下层股线最大值低于上层股线约2.5 K,最高温升处至股线端部,股线沿轴向长度温升急剧下降,且上层股线的下降速度比下层股线快。
从图8中可以看出转子股线最高温升位于0.55 m处的转子铁心段内,最低温升在电机转子铁心段的进风端,在铁心段内转子股线温升变化较快,相差约25 K。
4.3 电机齿部温升分布
在研究股线沿轴向长度温升分布的同时有必要对铁心沿轴向长度温升分布进行研究,图9为定子铁心径向不同高度温升分布,图10为转子齿径向不同高度温升分布。

图9 定子铁心径向不同高度温升分布Fig.9 Radial Temperature distribution of generator stator core at different height
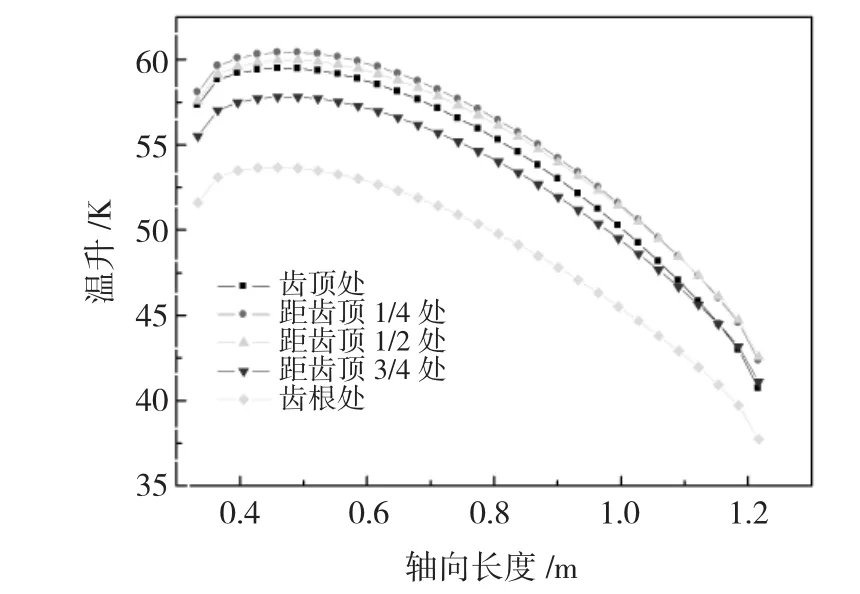
图10 转子齿径向不同高度温升分布Fig.10 Radial temperature distribution of generator rotor at different height
图9给出了定子铁心内轭背处、距轭背1/2轭高处、齿根处、距齿顶1/2高处及齿顶处的温升分布情况。由图9可知,在定子铁心径向不同位置温升相差很大,这是由于定子中产生的热量大部分向轭背部传导,硅钢片是热的良导体,越靠近轭背越有利于导热;不同位置沿轴向长度温升呈上升趋势,只是径向不同位置温升变化趋势不同,轭背处、距轭背部1/2轭高处、齿根处、距齿顶1/2高处变化趋势一致,沿轴向长度逐渐增大;气隙中空气在流通过程中要带走定子产生的一小部分热量,空气在气隙中流动的过程温升变化较快,对齿顶的散热有影响,齿顶处温升沿轴向长度温升变化较大。
图10中分别为转子齿顶处、齿1/4处、齿1/2处、齿3/4处及齿根处沿轴向长度温升分布,从图中可以看出转子齿不同高度沿轴向长度变化一致,最高温升所在同一轴向截面上,最高约为62K;转子齿部沿轴向不同截面最高温升约在距齿顶1/4处;虽然齿顶距离转子通风孔最远,向转子通风孔传热最为困难,齿顶处温升却不是太高,最大值为58.3K,是由于齿顶处和槽楔紧密接触,槽楔虽然导热能力差,但其不产生热量,齿顶的一部分热量向槽楔传导,又由于气隙中流动的空气也能带走一部分热量;齿根处距离转子通风孔最近,散热条件好,能够及时将自身产生的热量和齿部传导过来的热量传导给转子通风孔中的空气,在转子齿轴向截面中温升最低。
4.4 转子股线最高温升所在截面温升分布
因电机转子散热条件较恶劣,电机转子温升较高,有必要对电机最高温升处温升分布进行分析。由于电机转子各个相同位置温升分布规律一致,取电机转子任一股线最热面为研究对象,其温升分布如图11所示。
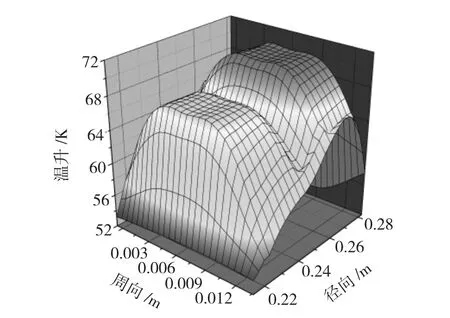
图11 转子股线轴向最热面温升分布图Fig.11 Temperature distribution of axial hottest surface of generator rotor
由图11可以看出,转子槽内温升分布随槽中心线对称分布;最高温升位于股线中心线上,沿铜块周围绝缘层温升下降明显,槽底和槽楔顶端散热条件较好,温升略低;上层股线温升高于下层股线,上下层股线之间相差3.2 K。
4.5 计算结果与实验值比较
发电机测温元件埋置在风扇端,距离发电机端部一定距离的定子绕组层间绝缘处,6个测温元件沿圆周方向均匀分布。表1给出了不同位置处的温度测量结果。

表1 温度测量结果Table 1 Measured data of temperature
根据表1的测量结果以及电机的实验环境温度,可以求出相应测量点的温升数值,进而获得电机的平均温升,如表1所示。
结合温度场求解域设定,可知求解域内有10处绕组层间绝缘位置处的温升可与实验值进行比较,温升数值计算结果及其平均值与实验值的对比如表2所示。

表2 计算值与实验值比较Table 2 Comparison of calculated value with measured data
通过对表2中的数值进行对比分析以及对温升计算结果的研究,可知:不同绕组层间绝缘在测量位置处的温升计算结果差值较小;不同位置处的计算值均比实验平均值低,最大相差5.34 K,最小误差为0.17 K;温升计算平均值比实验平均值低2.63 K,误差为4.24%,计算结果与实验结果相吻合。
以上结果可能由于电机端部流体流动紊乱以及将电机静止处理而转子通风孔并非完全对称的缘故造成。
5 结论
本文通过对1.5 MW双馈发电机三维温度场的计算以及对流体流动特性的分析,可以得出以下结论:
1)计算结果与实验数值相比较误差为4.24%,能够满足工程需要,验证了结果的准确性,说明文中所采用有限体积法计算温度场和流体场的方法可行,为发电机的运行以及大容量发电机设计有指导义。
2)从本文的分析和计算,电机转子热量要经过两次传导才能将热量带到电机外部,发电机转子在电机中的温升较高。
3)得出电机各部分温升分布及电机内流体分布规律,为测温元件的布置做理论指导。
4)在实际运行过程中应加强对端部股线温度监测,此部位由于绝缘材料导热系数小,空气流体绕流复杂,散热条件最为恶劣,温升较高,是电机温度监测的重点区域。
[1] 侯侠,王静.21世纪的绿色能源[J].内蒙古石油化工,2006(12):52-54.
HOU Xia,WANG Jing.Green energy of 21 centuries[J].Inner Mongolia Petrochemical Industry,2006(12):52 -54.
[2] 程明,张运乾,张建忠.风力发电机发展现状及研究进展[J].电力科学与技术学报,2009,24(3):2-9.
CHENG Ming,ZHANG Yunqian,ZHANG Jianzhong.Development and research progress of wind power generator[J].Journal of Electrical Power Science and Technology,2009,24(3):2 -9.
[3] 尹超.浅谈我国风力发电的现状和前景[J].山东电力技术,2009(6):14-15.
YIN Chao.Brief discussion on the present situation and prospects of wind power generation in china[J].Shandong Electric Power,2009(6):14-15.
[4] 施跃文,高辉,陈钟.特大型风力发电机组技术现状与发展趋势[J].神华科技,2009,7(2):34 -38.
SHI Yuewen,GAO Hui,CHEN Zhong.Technological development trends of super-large wind generating set[J].Shenhua Science and Technology,2009,7(2):34 -38.
[5] 李和明,李俊卿.电机中温度计算方法及其应用综述[J].华北电力大学学报,2005,32(1):1 -5.
LI Heming,LI Junqing.Summarization on the temperature computation and application in electric machines[J].Journal of North China Electric Power University,2005,32(1):1 -5.
[6] 鲁涤强,黄学良,胡敏强.汽轮发电机端部三维温度场的有限元计算[J].中国电机工程学报,2001,21(3):82 -85.
LU Diqiang,HUANG Xueliang,HU Minqiang.Using finite element method to calculate 3d thermal distribution in the end region of turbo generator[J].Proceedings of the CSEE,2001,21(3):82 -85.
[7] BOGLIETTI A,CAVAGNINO A,STATON D,et al.Evolution and modern approaches for thermal analysis of electrical machines[J].IEEE Transactions on Industrial Electronics,2009,56(3):871-882.
[8] 曹君慈,李伟力,程树康.复合笼条转子感应电动机温度场计算及相关性分析[J].中国电机工程学报,2008,28(30):96-102.CAO Junci,LI Weili,CHENG Shukang.Temperature field calculation and associated factor analysis of induction motor with compound cage rotor[J].Proceedings of the CSEE,2008,28(30):96-102.
[9] 温志伟,顾国彪,王海峰.浸润式与强迫内冷结合的蒸发冷却汽轮发电机定子三维温度场计算[J].中国电机工程学报,2006,26(23):133 -138.
WEN Zhiwei,GU Guobiao,WANG haifeng.Calculation of 3D thermal field in the stator of turbo-generator with immersion evaporative-cooling system and forced inner-cooling[J].Proceedings of the CSEE,2006,26(23):133 -138.
[10] 霍菲,张晓晨,程鹏.屏蔽电机定子温度场的数值计算与分析[J].电机与控制应用,2006,33(4):7 -12.
HUO Fei,ZHANG Xiaochen,CHENG Peng.Numerical calculation and analysis of temperature field of canned motor stator[J].Electric Machines & Control Application,2006,33(4):7 -12.
[11] 刘长红,姚若萍.自循环蒸发冷却电机定子铁心与绕组间的热量传递[J].中国电机工程学报,2008,28(11):107 -112.
LIU Changhong,YAO Ruoping.Heat transfer between stator core and windings in hydro-generators with self pump circulated evaporation cooling system [J].Proceedings of the CSEE,2008,28(11):107-112.
[12] 路义萍,陈朋飞,李俊亭,等.某新型空冷汽轮发电机转子通风方式的流场分析[J].中国电机工程学报,2010,30(6):63-68.
LU Yiping,CHEN Pengfei,LI Junting,et al.Flow field analysis of new type ventilation method in one air-cooled turbo-generator rotor[J].Proceedings of the CSEE,2010,30(6):65 -67.
[13] 李伟力,杨雪峰,顾德宝.空冷汽轮发电机冷却气流风量对定子内流体的影响[J].中国电机工程学报,2009,30(21):53-61.
LI Weili,YANG Xuefeng,GU Debao.Influence of air current flow change on fluid flow and heat transfer of air-cooled turbo-generator with multipath ventilation[J].Proceedings of the CSEE,2009,30(21):53 -61.
[14] 章梓雄,董曾南.粘性流体力学[M].北京:清华大学出版社,1998:255-279.
[15] 鲍里先科 A N.电机中的空气动力学与热传递[M].北京:机械工业出版社,1985:121-183.
[16] 陶文铨.数值传热学[M].西安:西安交通大学出版社,2001:347-353.
[17] 周俊杰,徐国权,张华俊.FLUENT工程技术与实例分析[M].北京:中国水利水电出版社,2010:14-17.
[18] 丁舜年.大型电机的发热与冷却[M].北京:科学出版社,1992.

