扰动补偿的陀螺稳定平台单神经元自适应PI控制

朱海荣， 李奇， 顾菊平， 李俊红

(1.东南大学自动化学院，江苏南京210096;2.南通大学电气工程学院，江苏南通226019)

0 引言

陀螺稳定平台广泛应用于精确制导武器、机载光电侦查设备、坦克火控瞄准系统、车载卫星通信设备等领域，其主要作用是隔离载体扰动，使负载(如各类探测装置、天线、炮塔等)在惯性空间保持稳定［1］。目前陀螺稳定平台控制大多基于传统的频域设计理论，一般采用典型的双闭环(速度环+位置环)或三环结构(电流环+速度环+位置环)结构，通过各闭环系统校正，实现对平台的控制。但陀螺稳定平台受摩擦力矩、载体扰动力矩、质量不平衡力矩等未知非线性扰动的影响，经典控制难以对系统中的各种非线性因素进行有效的抑制，如何保证稳定平台对姿态扰动信号的有效隔离，减小探测装置的抖动，一直是困扰工程技术人员的难点［2］。

近几年，神经网络［3］、H∞控制［4］以及模糊控制［5］等先进控制方法已经逐渐应用于陀螺稳定平台的控制中，通过理论分析证明了这些先进控制方法能抑制平台中非线性干扰力矩的影响，但算法不够完善，可靠性和实时性均存在一定程度的不足，真正在实际系统中得到应用的尚不多见。

本文提出了一种基于扰动补偿的单神经元自适应PI控制策略，单神经元结构简单，利用其自学习、自组织能力，根据被控对象的变化情况对控制器的权值进行在线调整［6］;而扰动观测器(DOB)不需要对干扰信号建立准确的数学模型，在观测干扰信号时避免了大量的数学计算，能够很好地满足实时性需要［7－9］。最后在测试转台上对陀螺稳定平台进行了相关测试实验，实验结果表明了该算法具有很高的实时性，能有效提高系统控制品质与抗干扰性能，具有工程实际意义。

1 系统数学模型

稳定平台控制系统调速范围较宽，特别有低速要求，一般采用直流力矩电机直接驱动。图1是单轴平台示意图，以惯性空间为参照系，θb是载体的旋转角度，载体运动会耦合到稳定平台，安装在平台上的速率陀螺可以敏感其在惯性空间的角速度，θl即是稳定平台的旋转角度，由此得出平台相对载体的旋转角度 θ=θl－θb，θ即为电机的转角。

根据直流力矩电机原理，电压平衡方程为

转矩方程为

其中:u(t)为电枢控制电压;i(t)为电枢电流;L为电枢回路总电感;R为电枢回路总电阻;J为等效到转轴上的转动惯量，J=Jm+JL，Jm和JL分别为电机和负载的转动惯量;θ(t)为电机的角位移;b为粘性阻尼系数，b=bm+bL，bm和bL分别为电机和负载的粘性阻尼系数;Km为电机力矩系数;T∑为加在电机转轴上各种扰动力矩总和。

图1 单轴平台示意图Fig.1 Schem of single-axis platform

2 基于扰动补偿的单神经元PI控制器设计

2.1 电流环设计

图2是电流环控制框图，电流环集成在电机功率放大器内，从稳态要求上看，希望实际电流跟踪指令电流无静差，从动态性能上看，希望实际电流超调小、响应快，以跟踪性能为主。电流环采用PI控制器，经过校正后的电流环可以提高电机响应时间、拓展频率带宽，抑制由电网电压波动造成的不利影响，通过在电流环设置电流最大值，可以实现对电机的自动保护。

图2 电流环控制框图Fig.2 Structure of current-loop control

2.2 速度环控制器设计

在速度环控制中，通常采用传统的PI控制器。PI控制具有结构简单，控制算法易实现等优点，但固定参数的PI控制器无法解决快速性和稳态性能之间的矛盾;另外，PI控制是根据误差进行调整的控制策略，不能对陀螺稳定平台运行中的未知非线性干扰进行快速隔离。对此，速度环采用了基于扰动观测器的单神经元自适应PI控制器，其模型结构方框图如图3所示。从图3可以看出，整个控制系统主要由两个部分组成，分别为一个单神经元自适应PI控制器和一个扰动观测器。其设计的基本思路是:首先设计扰动观测器，把实际系统输出与参考模型输出的差异作为一个等效的干扰，DOB估计出这个等效干扰，并将其作为一个补偿信号前馈到控制输入端，以消除干扰对系统性能的影响;在此基础上，设计单神经元自适应PI控制器做为反馈控制器，可以根据运行过程自适应调整参数，从而大大提高系统的控制能力和抗干扰能力。

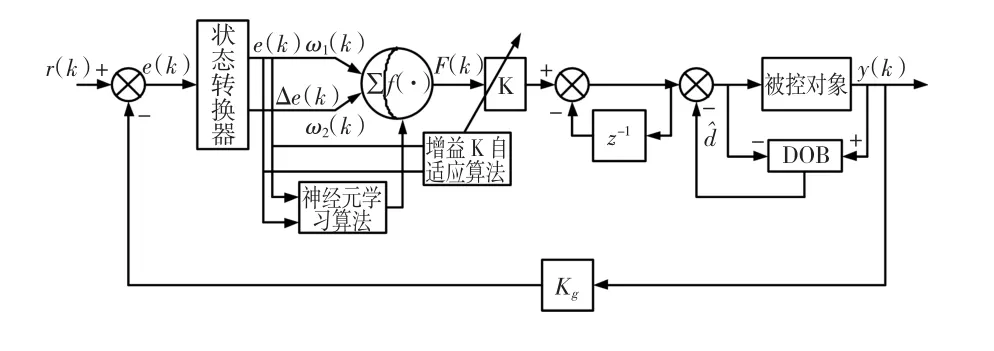
图3 速度环控制原理框图Fig.3 Scheme of speed-loop control

2.3 扰动观测器设计

扰动观测器(DOB)的基本结构如图4所示，dexuo、u、ξ、y 分别为输入扰动、干扰观测值、控制器输出、总控制输入、测量噪声和系统输出［10］。图中Gp(s)为实际对象模型，Gn(s)是系统参考模型，Q(s)为低通滤波器。从图4可以得到输出y的表达式为

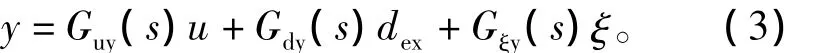
其中:

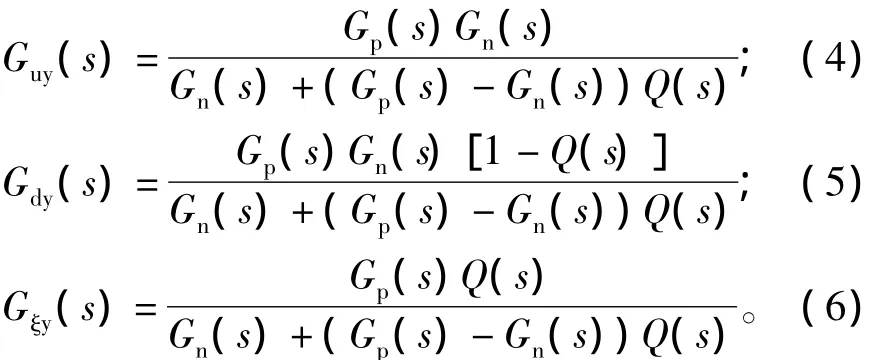
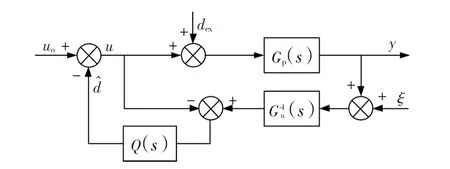
图4 扰动观测器结构图Fig.4 Structure of DOB

设低通滤波器Q(s)的频带为fq。当系统频带f≤fq时，Q(s)≈1，Guy(s)≈Gn(s)，Gdy(s)≈0，Gξy(s)≈－1，扰动观测器使得实际装置与参考模型相似，具备强的抗扰动性能，同时扰动观测的前馈量会引入噪声;当 f＞ fq时，Q(s)≈0，Guy(s)≈Gp(s)，Gdy(s)≈Gp(s)，Gξy(s)≈0，扰动观测器环相当于开环，没有前馈作用，因而不会由于加入扰动观测器而引入测量噪声［11］。一般地，系统的噪声是高频的，所以因扰动观测器而引入的噪声对系统控制性能影响不会特别严重［12］。

由电机的转矩方程(2)可得

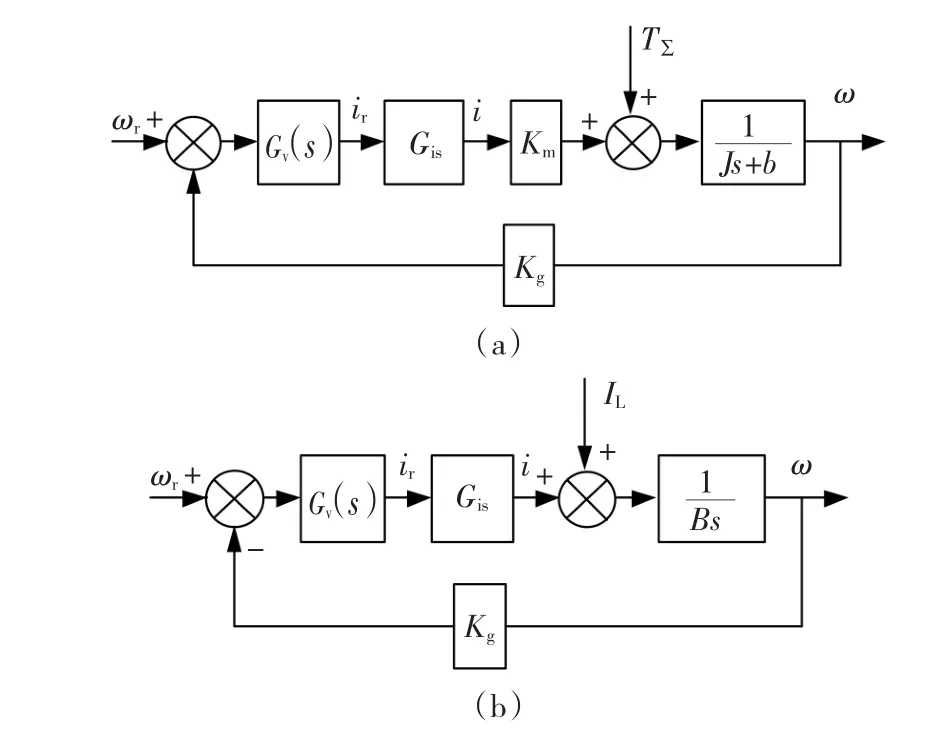
图5 速度环结构框图Fig.5 Structure of speed control

由于电流变化比较快，在速度环扰动观测器的设计过程中，可以将电流环等效成增益固定的比例环节。在所论述的稳定平台力矩电机控制方案框架内，无论外部扰动、内部扰动以何种形式存在，我们对其观测最终都将以电流形式进行补偿。故将扰动对应成电流形式，式(7)变化为其中:B=J/Km;IL=－w/Km为电流形式的负载扰动。相应地，将电机速度环结构框图5(a)转化成图5(b)。

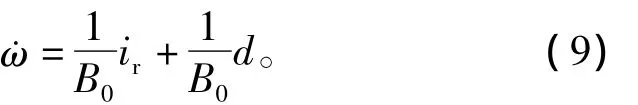
其中，d=IL+B0˙ω－B˙ω+i－ir，可看成是一种包括负载扰动、模型失配、电流环跟踪误差在内的等价扰动。此时有

根据扰动观测器结构框图(4)可知，扰动观测器输出为

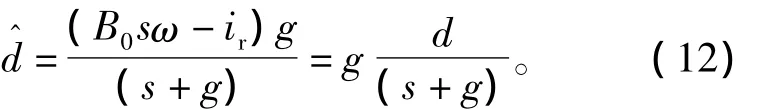
由式(12)可知，扰动观测器中滤波器参数g→∞，则^d→d，即扰动观测器的观测值跟踪上实际扰动值，通过前馈控制实现对干扰的补偿。

2.4 单神经元自适应PI控制器设计

单神经元自适应控制器的控制律设计为

式中:

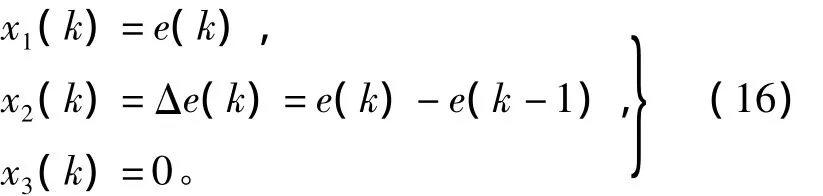
其中:e(k)为控制系统的偏差信号;Δe(k)为控制器的偏差一次微分输入;ωi(k)为控制器参数的加权值;r(k)为k时刻被控量的设定值;u(k)为控制器k时刻的输出值。

单神经元自适应控制器是通过对权系数ωi的调整来实现自适应、自组织功能，采用的学习策略对控制器的自适应能力及稳定性能都有很大影响，权系数的调整是按有监督的Hebb学习规则实现的。实践表明，PI参数的在线学习修正主要与Δe(k)和Δe(k)有关。因此可将加权系数学习修正部分进行修改，改进后的学习算法为

其中:xi(k)=e(k)+Δe(k)=2e(k)－e(k－1)i=(1，2);学习速率ηP、ηI由仿真实验按时间乘绝对误差积分准则(ITAE)选定不同值为佳。

由Marsik［14］等给出的增益自适应K(k)算法的递推算式为

阻尼指标参考值href，经过大量仿真实验寻优最终选定为0.15，在此具有最佳抗扰性能。L*为一正常数，0.05≤L*≤0.1;K(k)为k时刻控制器的总增益。

从式(18)～式(22)分析可知，K的初始值与控制系统的快速性、稳定性有密切关系。实验仿真表明当其取较小值时，控制系统响应变慢，超调量减少，但取得过小会使调整时间变长，稳态误差增大;当K的初始值取得较大时，系统调整时间变短，但响应曲线易振荡，超调量会变大。

3 实验研究

图6为某型号陀螺稳定平台实物图，最外面两个框架为扰动台，用于模拟载体扰动;内部两个框架为稳定平台，由外方位框和内俯仰框构成，电视跟踪装置安装在俯仰框，用于目标识别、给出脱靶量信号。以方位稳定框为例，采用Solid Edge V9对其进行建模后得到方位稳定框转动惯量为0.31 kg·m2，要求方位轴角速度≥40°/s，角加速度 ＞625°/s2，定位精度≤0.04°，过渡过程时间≤0.08s，稳定隔离精度＜0.2°(在10°/1Hz的正弦波扰动下)。根据上述指标，选用成都电机厂的分装式永磁式J130LYX05K型直流力矩电机，电机参数如下:连续堵转电压14 V，连续堵转电流5 A，连续堵转转矩5 Nm，峰值堵转电压27 V，峰值堵转电流10 A，峰值堵转转矩10 Nm，空载转速210 r/min，电气时间常数1.5 ms，电枢转动惯量0.006 kg·m2。选用俄罗斯Fizoptika公司的VG941－3AM型光纤速率陀螺作为速度反馈装置，具体参数如下:测速范围±500°，陀螺尺寸35 mm×35 mm×60 mm，启动时间0.1 s，偏差重复性0.003°/s，偏差变化，偏差稳定性，比例因子6 mV/(°)/s，比例因子重复性(稳态)0.1%，比例因子稳定性(稳态)0.03%，比例因子变化(OTR)5%，角度随机游走PSD0.0015deg/s/sqrtHz，频率范围0 ～500 Hz，振动6 g，20 ～2000 Hz，冲击加速度 90 g。选用 TMS320F2812 DSP作为主控芯片，通过DSP运动控制模块所配置的各类输入/输出模块接口，接收速率陀螺信号、读取控制IO信号量、输出控制信号。通过USB2.0标准的高速串行总线接口实现与计算机监控系统间的数据交换:接收计算机监控系统发送来的运动参数、数字指令，经过计算后产生相应的伺服驱动命令;同时向计算机监控系统传送稳定平台各轴系的实时数据及状态信息。

图6 陀螺稳定平台实物图Fig.6 Photo of a gyrostabilized platform

将控制量和扰动观测器离散化，得

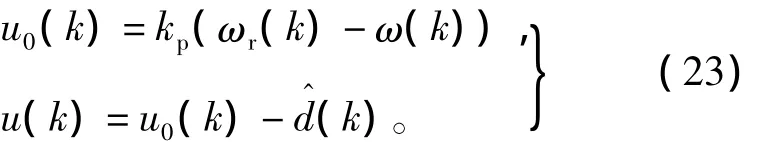
其中，

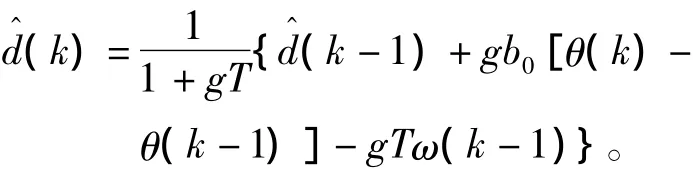
首先确定DOB参数b0=1.05，g=0.13。实验时，选择跟踪目标为静止的状态(此时的脱靶量信号为零，要求陀螺稳定平台保持静止，速度和位置信号均为零)，分别给定5°/0.5 Hz、10°/1 Hz两组模拟载体扰动信号，对方位稳定框进行性能测试。位置环均采用PID控制，速度环分别采用常规PI控制，PI+DOB控制，及基于扰动观测器的单神经元PI控制策略。为了使对比客观，通过多次调试，先把上述三种控制策略均调到相对最优的情况，使系统具有较好的动静态性能，再分别进行对比分析。

图7(a)、(b)、(c)分别为 5°/0.5 Hz载体扰动下采用上述3种控制策略时的抗扰动性能测试曲线，包括位置误差曲线和速度误差曲线。由实验结果可以看出:载体运行会对系统产生各种扰动影响，尤其在载体换向时，轴系摩擦在动摩擦和静摩擦之间发生突变，此时对系统影响最为明显，具体表现为稳定跟踪误差曲线在此处出现尖峰，跟踪误差最大，而速度误差曲线的毛刺信号幅值增大，引起探测装置的抖振。

图7 5°/0.5 Hz扰动信号下抗扰动性能对比Fig.7 Contrast of anti-disturbance ability under external disturbance of 5°/0.5 Hz

为了进一步对控制效果进行对比，把载体运行的幅值和频率逐步增大，图8(a)、(b)、(c)分别为10°/1 Hz载体扰动下采用上述3种控制策略时的抗扰动性能测试曲线。由实验结果可以看出:载体运行的幅值和频率增大后，对稳定平台的影响随之增大，具体表现在位置误差增大、速度抖动更加明显。

图8 10°/1 Hz扰动信号下抗扰动性能测试曲线Fig.8 Contrast of anti-disturbance ability under external disturbance of 10°/1 Hz

经过分析对比发现，采用常规PI控制时，在载体扰动幅值、频率较低的情形下尚能达到设计指标，但随着载体扰动影响的加大，其抗扰动性能变差，在10°/1 Hz载体扰动下的稳定隔离精度＞0.2°，达不到设计指标的要求;加入扰动观测器后，可以对系统扰动实现部分补偿，系统抗扰动性能得到了提高，由于此时PI参数是固定的，在外界扰动发生变化后缺乏很好的自适应性，误差仍然偏大;采用单神经元自适应PI+DOB控制后，在测试范围内的各种频率和幅值的干扰下都体现出了很好的扰动隔离能力。以上分析说明了本文所提出的控制策略在陀螺稳定平台的控制中是有效可行的，大大改善了控制系统的抗干扰能力与系统性能。

4 结语

本文介绍了陀螺稳定平台伺服控制系统速度回路的设计过程，该回路的设计必须从跟随指令输入、克服摩擦等干扰力矩和隔离载体耦合扰动三个方面考虑。针对平台受载体扰动、风阻力矩、气流、波浪等未知干扰的影响，设计了基于扰动补偿的单神经元自适应PI控制策略，并在某型号陀螺稳定平台上得到了很好的工程应用。实验结果表明，该控制方法能对载体运动引起的不确定扰动进行补偿，提高了系统的抗干扰性能和鲁棒性，具有很高的推广价值和工程应用前景。

［1］ HILKERT J M.Inertially stabilized platform technology concepts and principles［J］.IEEE Control Systems Magazine，2008，28(1):26－46.

［2］ VELLA F，CASTORINA A，MANCUAO M.Digital image stabilization by adaptive block motion vectors filtering［J］.IEEE Transactions on Consumer Electronics，2002，19(2):796 －801.

［3］ TAN K C，LEE T H，KHOR E F.Design and real-time implementation of a multivariable gyro-mirror line-of-sight stabilization platform［J］.Fuzzy Sets and Systems，2002，128(1):81 －93.

［4］ KRISHNA MOORTY J A R，MARATHE Rajeev，SULE V R.H∞Control law for line-of-sight stabilization for mobile land vehicles［J］.Optical Engineering，2002，41(11):2935 －2944.

［5］ KRISHNA MOORTY J A R，MARATHE Rajeev，HARI B.Fuzzy controller for line of sight stabilization system［J］.Optical Engineering，2004，43(6):1394 －1400.

［6］ 赵锡龄，焦云婷.单神经元自适应控制PSD在再热汽温控制中的应用［J］.中国电机工程学报，2001，21(2):93 －96.

ZHAO Xiling，JIAO Yunting.Single neuron self-adaptive PSD Control and its application in reheat steam temperature control system［J］.Proceedings of the CSEE，2001，21(2):93 －96.

［7］ 赵振民，刘锋，孔民秀，等.高速并联机械手臂的自抗扰控制算法研究［J］.电机与控制学报，2011，15(1):98 －104.

ZHAO Zhenmin，LIU Feng，KONG Minxiu，et al［J］.Electric Machines and Control，2011，15(1):98 －104.

［8］ SHIMA Hyungbo，NAM H Jo.An almost necessary and sufficient condition for robust stability of closed-loop systems with disturbance observer［J］.Automatica，2009，45(1):296 －299.

［9］ 何朕，王广雄.悬吊减重系统的力控制［J］.电机与控制学报，2010，14(11):82 －87.

HE Zhen，WANG Guangxiong.Force control of a partial weight support system［J］.Electric Machines and Control，2010，14(11):82－87.

［10］ TEOH JN，DU C.Rejecting high frequency disturbances with disturbance observer and phase stabilized control［J］.Mechatronics，2008，18(2):53－60.

［11］ 周文雅，何朕，王毅.扰动观测器和等价性［J］.电机与控制学报，2006，10(3):256 －259.

ZHOU Wenya，HE Zheng，WANG Yi.Disturbance observer and its equivalence［J］.Electric Machines and Control，2006，10(3):256－259.

［12］ 方一鸣，王乐.基于等效负载扰动观测器的直流电机转速鲁棒控制［J］.电机与控制学报，2002，6(4):297 －300.

FANG Yiming，WANG Le.The robust speed control of a DC motor based on the equivalent load observer［J］.Electric Machines and Control，2002，6(4):297 －300.

［13］ LI S H，LIU Z G.Adaptive speed control for permanent magnet synchronous motor system with variations of load inertia［J］.IEEE Transactions on Industrial Electronics，2009，56(8):3050－3059.

［14］ MARSIK J.A new conception of digital adaptive PSD control［J］.Problem of Control and Information Theory，1983(12):267－277.