单位阶跃响应的时域求解方法

任 蕾，薄 华，金欣磊，张韵农，杨忠根

(上海海事大学电子工程系，上海200135)

单位阶跃响应的概念和求解是“信号与系统”课程教学的重要知识点之一。目前，多数教材中给出单位冲激响应的时域方法［1-6]，国内的部分学者也总结了冲激响应时域求解的多种求解方法［7]。单位阶跃响应可通过对冲激响应积分或将其与单位阶跃信号卷积，在时域中求解。

本文从冲激响应与阶跃响应的关系、微分方程求解和时域规范化方法三个角度出发，讨论单位阶跃响应的时域一般求解方法，并给予实例证明方法的有效性。

1 单位阶跃响应的时域求解方法

1.1 问题描述

设线性时不变系统的微分方程为式中，f(t)是系统的激励信号，系统初始条件为，y(t)是系统的响应信号。

1.2 单位阶跃响应的时域求解方法

(1)利用单位冲激响应求解阶跃响应

通过对冲激响应的积分运算或与单位阶跃信号的卷积，可得系统的阶跃响应:

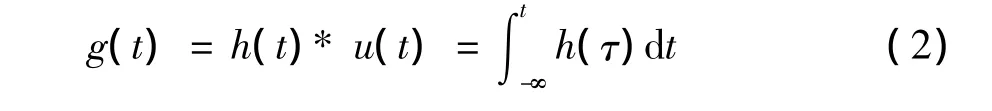
该方法概念清楚，但需首先求解系统的单位冲激响应。值得注意的是，系统的冲激响应即为系统的阶跃响应。

(2)微分方程求解的方法

由于系统阶跃响应是系统的零状态响应，因此可利用经典微分方程求解方法求解。

将单位阶跃信号代入微分方程，可得阶跃响应即为求解方程:

(3)时域规范化方法

［思路1] :受单位冲激响应规范化方法的启发，可得规范化单位阶跃响应求解方法。

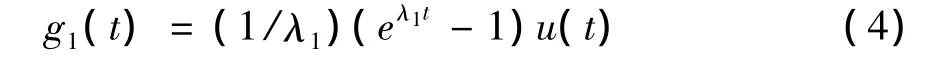
第二个子系统和各规范化子系统的冲激响应分别为

规范化系统的阶跃响应为

［思路2] :借鉴文献［6] 中等效激励方法，阶跃响应也可按如下步骤进行。

①首先求解对应的规范化系统冲激响应hx(t);

规范化方法不受n与m大小的影响，同时避免了系统初始条件求解，较为简便。

1.3 三种方法的对比

为了说明上述三个方法的特点，其对比见表1。

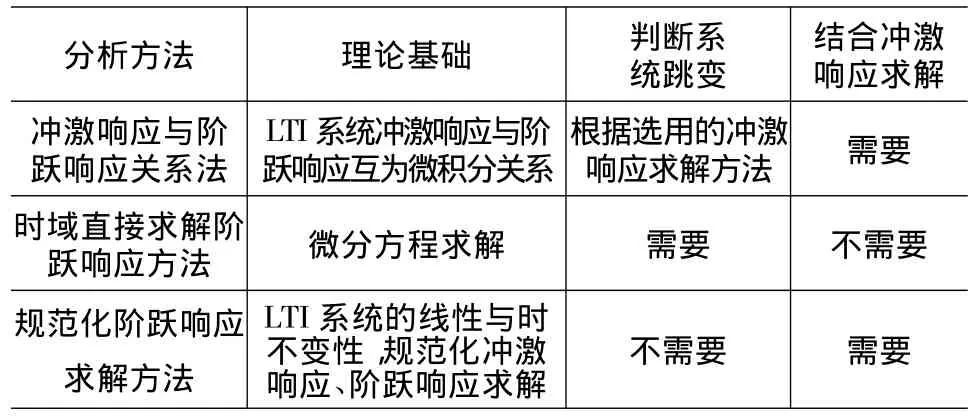
表1 :单位阶跃响应时域求解方法对比表

可以看出，利用冲激响应与阶跃响应微积分关系的方法，是最常用的方法，其前提是计算系统的冲激响应;时域直接求解阶跃响应的方法，概念较清楚，无需求解系统的冲激响应，其难点在于判断系统0+时刻的初始条件;规范化阶跃响应求解方法，借鉴了规范法冲激响应求解方法，该方法无需判断求解系统的初始条件。

2 单位阶段响应时域求解举例

为了说明给出的单位阶跃响应时域求解方法的有效性，下面以两个实际例子说明其应用过程，分别对应微分方程中n＞m和n=m两类情况。

［例1] :下述某线性时不变系统微分方程为

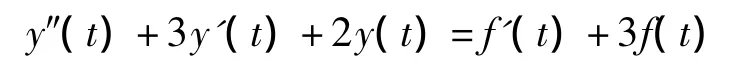
试求系统的单位阶跃响应。

解:该系统为二阶系统，对应n＞m情况，可采用如下三种方法。

(1)单位冲激响应间接求解方法

首先利用时域方法(可以任意选择一种)求解该系统的单位冲激响应为

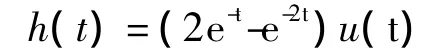
因此，通过对其卷积单位阶跃信号(或对冲激响应做积分运算)得到系统的单位阶跃响应为

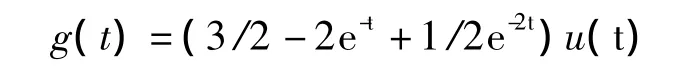
(2)直接求解阶跃响应方法

当系统激励信号为单位阶跃信号时，微分方程可以写为

因此，设阶跃响应的形式写为

由方程得gp(t)=(3/2)u(t)，且g(0+)=g(0－)=0，g'(0+)=g'(0－)+1=1，由此确定待定系数:A1=－2，A2=1/2。

可得系统的单位阶跃响应为

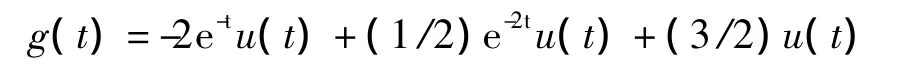
(3)规范化求解方法

我们利用求解方法(3)的思路，首先求解对应的规范化一阶系统g1'(t)+g1(t)=u(t)的阶跃响应为g1(t)=-e－tu(t)+u(t)。则该规范化二阶系统的阶跃响应为

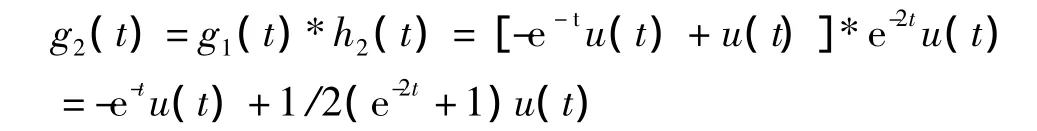
可得原系统阶跃响应为

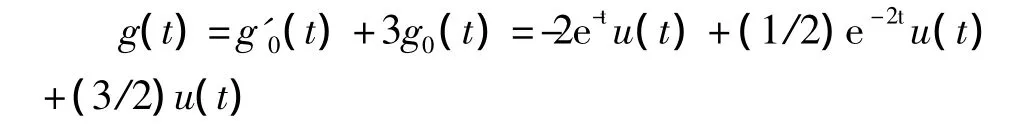
［例2] :下述某线性时不变系统微分方程为

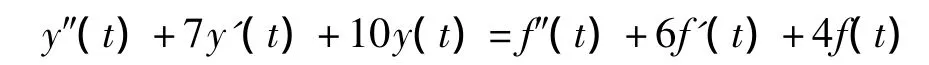
试求系统的单位阶跃响应。

解:该系统为二阶系统，对应n=m情况，可采用如下三种方法。

(1)单位冲激响应间接求解方法

首先利用时域方法(可以任意选择一种)求解该系统的单位冲激响应为

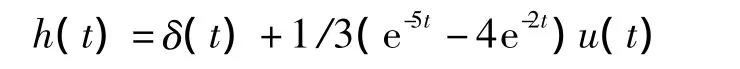
因此，通过对其卷积单位阶跃信号(或对冲激响应做积分运算)得到系统的单位阶跃响应为

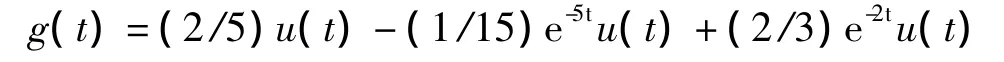
(2)直接求解阶跃响应方法

当系统激励信号为单位阶跃信号时，微分方程可以写成为

因此设阶跃响应的形式为

由方程得:gp(t)=(2/5)u(t);且g(0+)=g(0－)+1，g'(0+)=g'(0－)－1=-1由此确定待定系数为A1=2/3，A2=-1/15。

系统的单位阶跃响应为

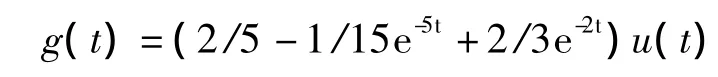
(3)规范化求解方法

我们利用思路2求解该题，该系统对应规范化系统冲激响应为hx(t)=e-2tu(t)*e-5tu(t)=1/3(e-2t－e-5t)u(t)，且等效零状态激励为xg(t)=δ'(t)+6δ(t)+4u(t)。

可得系统的单位活跃响应为

3 结语

本文对连续时间系统单位阶跃响应的时域求解方法进行了总结和归纳。这些种方法提供了直接求解或结合单位冲激响应求解的阶跃响应时域分析思路，可根据具体的情况选择。

［1] 奥本海姆著，刘树棠译.信号与系统(第二版)［M] .西安:西安交通大学出版社，1998

［2] 郑君里，应启珩，杨为理.信号与系统［M] .北京:高等教育出版社，2000

［3] 管致中，夏恭恪，孟桥.信号与线性系统(第四版)［M] .北京:高等教育出版社，2004

［4] 吴大正，信号与线性系统分析(第四版)［M] .北京:高等教育出版社，2006

［5] B.P拉兹著，刘树棠等译.线性系统与信号(第2版)［M] .西安:西安交通大学出版社，2006

［6] 杨忠根，任蕾，陈红亮，信号与系统［M] .北京:电子工业出版社，2009

［7] 杜世民，杨润萍，LTI系统单位冲激响应的时域解法研究［J] .南京:电气电子教学学报，Vol.29，No.5，2007年10月，44-46