减阻水溶液槽道湍流特性POD分析

蔡伟华，李凤臣，张红娜，王 悦，李小斌

(1.哈尔滨工业大学能源科学与工程学院，150001 哈尔滨;2.哈尔滨工业大学土木工程学院，150090 哈尔滨;3.哈尔滨工业大学市政环境工程学院，150090 哈尔滨)

减阻水溶液槽道湍流特性POD分析

蔡伟华1，2，3，李凤臣1，张红娜1，王 悦3)，李小斌1

(1.哈尔滨工业大学能源科学与工程学院，150001 哈尔滨;2.哈尔滨工业大学土木工程学院，150090 哈尔滨;3.哈尔滨工业大学市政环境工程学院，150090 哈尔滨)

为进一步分析减阻水溶液湍流减阻机理，对质量分数为30×10－6十六烷基三甲基氯化铵(CTAC)水溶液槽道湍流减阻流动进行了实验研究，并基于本征正交分解方法研究减阻水溶液流动中减阻剂对流动结构的影响.结果表明:CTAC水溶液流动在不同雷诺数(1.5×104、2.5×104和3.5×104)下分别具有65.1%、70.0%和33.0%减阻效果;基于本征正交分解方法分析湍流脉动速度场，发现CTAC添加剂能够抑制湍流猝发过程中的低速流体的上喷及高速流体的下扫，即在一定程度上抑制了相干结构的发生及其发展过程，最终导致湍流减阻.

减阻水溶液，湍流减阻，相干结构，本征正交分解，粒子图像测速仪

在液体湍流流动中加入少量的高聚物或某些表面活性剂可导致其湍流摩阻大幅度减少，称为添加剂湍流减阻(即 Toms效应［1］).高聚物和某些表面活性剂具有相同的减阻能力，其减阻率可高达80%［2］;但在强剪切力(如流过离心泵)、高温等因素作用下，高聚物的柔性长链分子结构易被破坏，且破坏后无法自动修复，导致其减阻效果的永久性丧失.某些表面活性剂由于具有良好的机械、化学、光和热稳定性，受到人们广泛的关注［3－4］，且其水溶液减阻效应的产生与消失是可逆的，可见其在集中供热与供冷系统中具有巨大的应用潜力.目前学术界对减阻机理还没有形成统一的理论，如 Lumley“黏性理论”［5］、湍流抑制假说［6］、弹性理论［7］等.研究表明，湍流减阻与近壁湍流猝发的相干结构有着密切的联系［8－9］.因此相干结构的研究对减阻湍流机理的认识具有重要意义.

如何客观理解和分析湍流相干结构进而揭示湍流物理机理是极其重要的.本征正交分解(POD)法，具有提取湍流流动中相干结构的功能，是一种强大的低维动力学分析方法.POD法，也称为 Karbunen－Loeve分解(K －L)［10］，其最主要的优势在于能够通过有限阶本征函数的线性组合来捕捉湍流流动中的相干结构［11－12］，其在湍流中的应用受到了广泛关注［13～16］.最近，Samanta和 Beris等［17－18］基于直接数值模拟(DNS)数据库并结合POD法研究黏弹性流体槽道湍流减阻流动特性.结果表明:在同一雷诺数下，与牛顿流体流动相比，流体黏弹性的存在对湍流特性产生重要的影响;通过前9个K－L基函数即可清晰地重构出流动中的大尺度结构;此外，对比分析DNS速度场和K－L重构速度场的能谱和耗散谱，发现K－L分解与重构过程能够有效地抑制流动中的小尺度结构，甚至抑制对湍流耗散贡献最大的小尺度结构.

本文首先利用粒子图像测速仪(PIV)测得水和十六烷基三甲基氯化铵(CTAC)水溶液槽道湍流流动瞬时速度场，并结合POD法提取流动中相干结构，分析其流动特性，进一步研究湍流减阻流动机理.

1 POD基本原理

1967年，Lumley［19］首次将 POD 法应用于湍流分析，并提出了将相干结构定义为空间变量的函数，从而使该函数具有最大的能量，即相干结构为本征函数φ(x)的线性组合，从而使

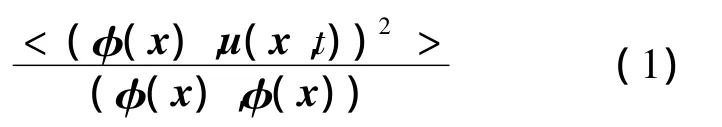
具有最大值.

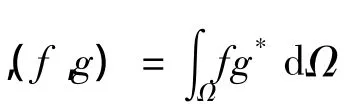
通过变量演化可知式(1)具有最大值的条件是φ(x)满足Fredholm积分方程的解，即

式中:R(x，x')=＜u(x)u(x')＞.

积分本征值/本征函数问题从理论上来说是一系列本征值/本征函数问题.相干结构被视为许多具有最大能量本征函数的线性组合.式(2)具有本征函数{φn(也称为经验本征函数，本征正交基)的集合，本征函数集是一个完备正交集，即

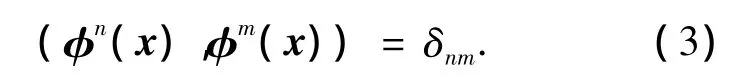
式中，δnm为Dirac函数.

速度场{uk(x)}中的每一个元素都可以由

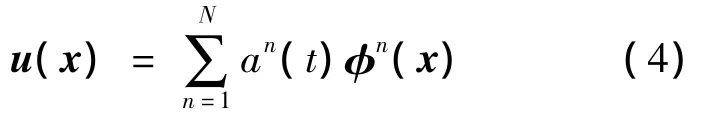
重构得到.式(4)中的重构系数an(t)可由

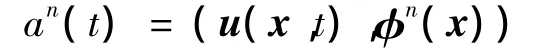
确定.an(t)2是流场u(x，t)在φn(x)方向上能量的总和.流场的总能量是an(t)2在不同方向上的能量的总和，即

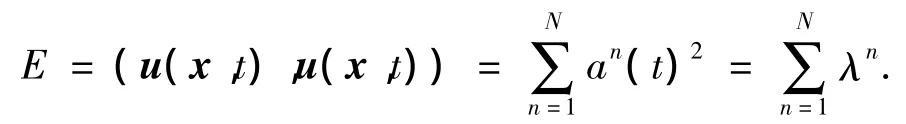
式中，E为平均流动湍动能的2倍.第n阶本征值λn代表第n阶本征函数的平均湍动能.

通过前K阶主要含能本征函数的重构来描述随机速度场的一个低维模型(通常本征函数和本征值按降序方法存储λn＞λn+1):

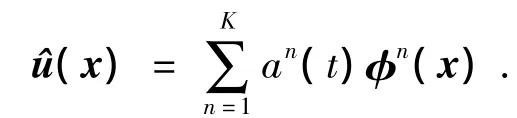
然而，基于PIV实验数据进行POD分析时，样本的数量通常比空间网格点少很多;因此，矩阵R(x，x')的解的数量不比样本的数量多，这就极大地减少了计算量，此POD法称之为Snapshot POD方法［20］.Snapshot POD方法能够有效地计算M个Snapshot(网格数为N)，当M ＜N时，利用M×M对称矩阵代替直接计算的自相关张量R(x，x')= ＜ u(x)u(x')＞:

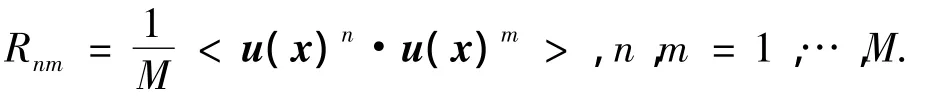
其中本征解σ(x)满足

POD本征函数可以通过式(5)本征解投影到原始速度场中，获得

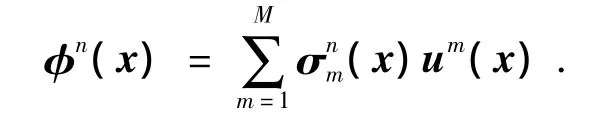
2 实验台简介及PIV测量

2.1 实验装置

实验在一个封闭循环水系统中进行，其测试实验段为一个二维槽道(10.00 m×0.04 m×0.50 m).在槽道入口上游处安置一个误差为±0.01 m3/min的电子流量计测量其流量.循环流动系统的水箱中装有冷却盘管和加热器，从而保证工作介质温度控制在304 K，其误差为±0.1 K.壁面剪切应力通过静压力梯度来估算，其测量通过槽道底面相隔1.5m距离的两个测压孔来完成，其误差为±0.1 Pa.关于实验台的详细介绍参见文献［4］.

2.2 工作介质

实验中使用CTAC添加剂，同时将与CTAC同等质量浓度的水杨酸钠(NaSal)加入水溶液中，提供反离子.Kawaguchi等［21］测量了 CTAC 水溶液的流变特性，结果表明:质量分数低于50×10－6CTAC水溶液的黏度与水的相比没有明显的差异.因此选取水的黏度来近似计算流动雷诺数(Re=U·H/υ［s］)，其中 U 为平均流速，H 为槽道的特征长度 H=0.04 m，υ［s］为水的黏度).

2.3 PIV测量系统

利用标准二维二分量(2D－2C)PIV系统测量槽道湍流流动的瞬时速度场.PIV系统主要部件为:双脉冲激光器(能量输出25 mJ/pulse，最大重复频率为20 Hz;CCD相机(像素为1 280×1 024，采样速率为8 Hz;因此速度场的采样频率为4 Hz).关于PIV的详细介绍参见文献［4］.

2.4 测量参数及结果

本文基于PIV系统测得水和质量分数为30×10－6CTAC水溶液在二维槽道中湍流流动瞬时速度矢量场.测量参数及结果如表1所示，φdr为减阻率，φdr=(－)/×100%，其中和分别为水和CTAC水溶液流动时的范宁摩擦因数.图1给出了范宁摩擦因数与雷诺数的关系.将图1中CTAC水溶液流动划分为4个状态.I区，无减阻现象发生;II区，随着雷诺数的增加，随之下降，当Re=ReC=2.5×104时(CB工况)，φdr达到最高值70.0%;III区，随着雷诺数的增加，随之增加，即φdr降低了;IV区，减阻现象消失.本文将对II区(CA)，临界雷诺数工况(CB)和III区(CC)CTAC水溶液流动特性进行分析与研究.

表1 测量参数及结果

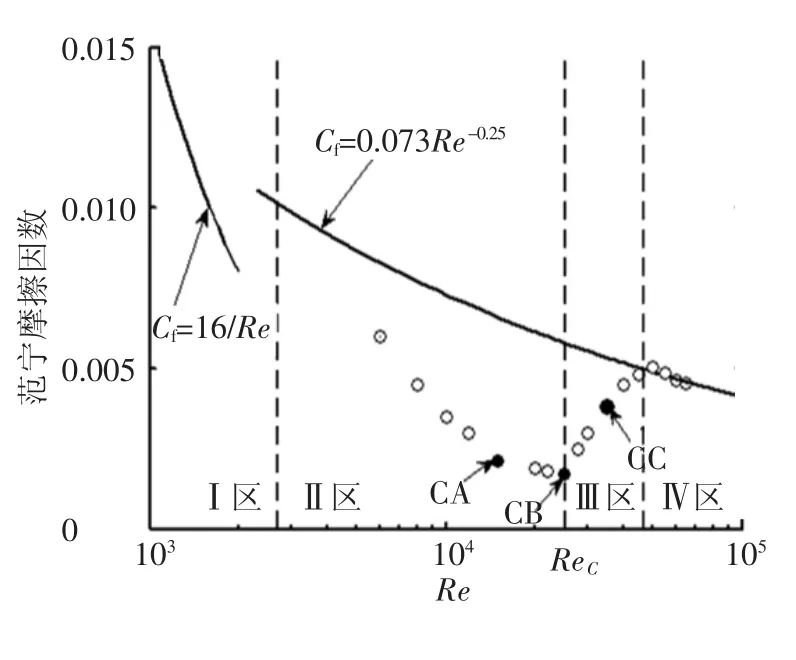
图1 范宁摩擦系数与雷诺数的关系

3 POD分析

基于POD法分析了水和质量分数为30×10－6CTAC水溶液在不同Re下的二维槽道湍流脉动速度场.表2列出了部分本征值及其捕捉的脉动能量.脉动速度场投影在本征函数φn(x)上的平均湍动能等于相应的本征值.结果表明:对于水流动来说，第1阶本征函数捕捉10.03%湍动能;而对于CA，CB和CC流动来说，第1阶本征函数分别捕捉24.72%，16.61%和10.86%的湍动能.此外，相干结构被视为许多具有最大能量的本征函数的线性组合，其具有90%的流动脉动能量.从表2可见，对于水、CA、CB和CC流动而言，捕捉相干结构分别需要233、105、195和243阶本征函数.

水和CTAC水溶液流动中本征函数累积贡献如图2所示.CA流动中本征函数累积贡献收敛最快，CB流动次之，而水和CC流动中本征函数累积贡献收敛比较慢.CC流动中虽具有33%的减阻率，但其雷诺数(3.5×104)比水(2.5×104)的雷诺数大，因此湍流脉动能分布在更多本征函数上.此外，还发现水和CTAC水溶液流动中均具有较宽POD能谱，因此流场重构需要较多本征函数，这充分说明了CTAC水溶液减阻流动仍处于湍流状态.

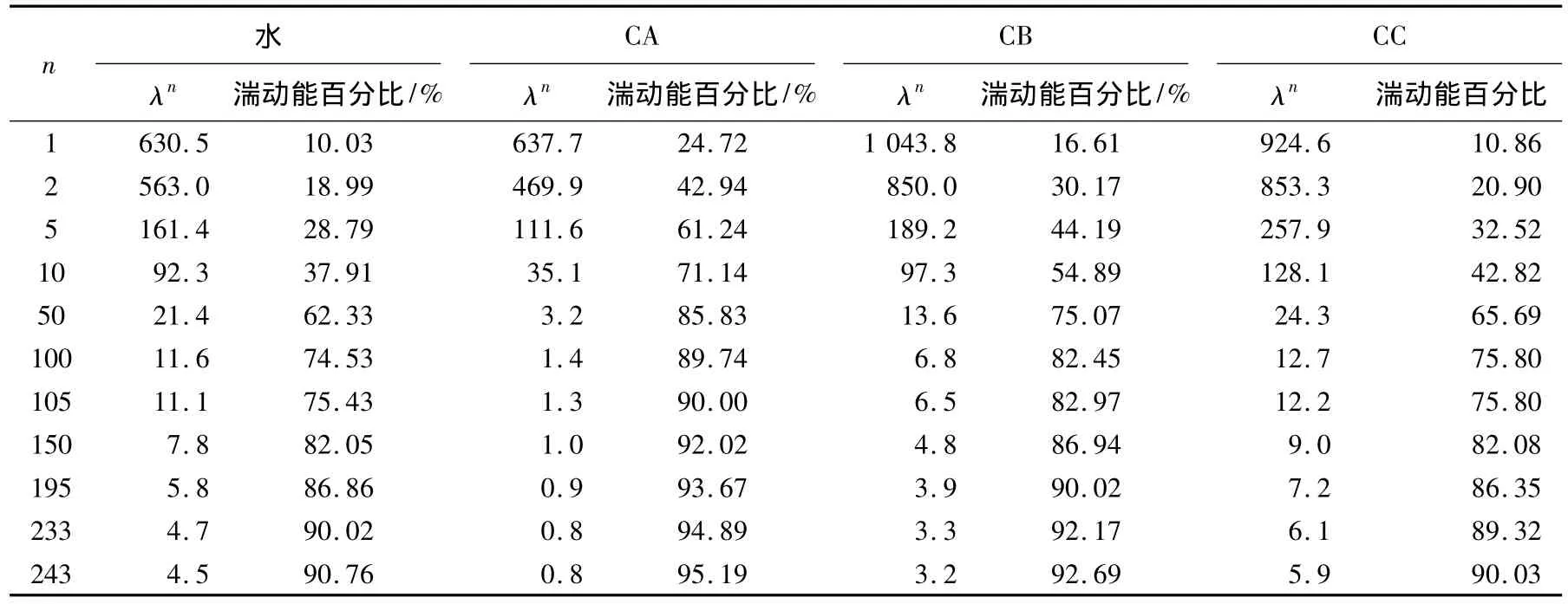
表2 水和CTAC水溶液流动中部分POD本征值及相对的能量

图2 水和CTAC水溶液流动中本征函数的累积贡献

POD本征函数描述了某一固定的基本空间结构，任意时刻的速度场可以通过这些空间结构的线性组合获得，因此研究本征函数对流场某些特性(如相干结构)有重要的意义.此外单独研究这些基本空间结构要比研究整个流场更加简单.本文研究分析水和CTAC水溶液流动的前4阶主要含能本征函数所捕捉到的流动结构.

图3给出了第1阶本征函数流场矢量图及流向速度云图(图中右上角处的速度为速度矢量参考值).可见，第1阶本征函数均捕捉到近壁面处大尺度流动特性;在CA流动中，近壁面处流动极其规则(速度矢量场与壁面平行)，这一方面是由于CTAC水溶液减阻所致，另一方面是雷诺数低的缘故.在CB流动中，近壁面处的速度矢量场也与壁面平行，这完全是CTAC水溶液减阻所致.然而在CC流动中，第1阶本征函数却捕捉到与水流动中的较为相似的近壁面处大尺度流动特性，但其强度明显要弱.这主要是雷诺数比较大，且该流动中仍存在33.0%减阻效果的缘故.

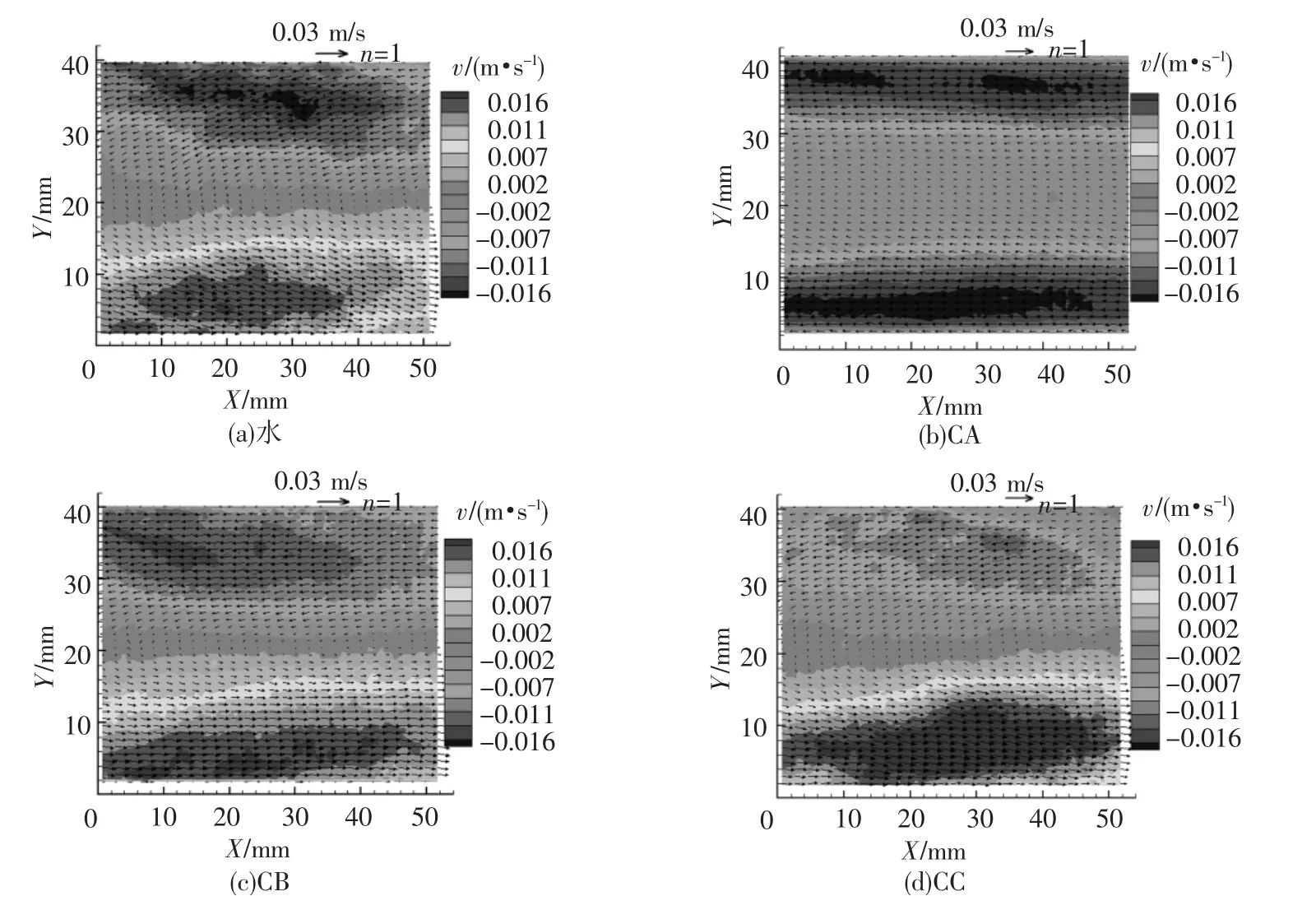
图3 水和CTAC水溶液流动中第1阶本征函数流场矢量图及流向速度云图

图4给出了第2阶本征函数流场矢量图及流 向速度云图(图中右上角处的速度为速度矢量参考值).可知，水和CC流动中近壁处的脉动结构均与壁面呈现一定的角度，而对于CA和CB流动来说，近壁处的脉动结构仍与壁面平行，且脉动值要小于水和CC流动，但CB流动中的脉动结构强度要大于CA流动中的.

根据前2阶本征函数结果，表明对于水和CTAC水溶液流动而言，前两阶本征函数均捕捉到壁面处流向脉动结构，且在一定程度上反映了流动特征，即对流场中湍动能贡献最大的流动结构均为近壁处的脉动结构.

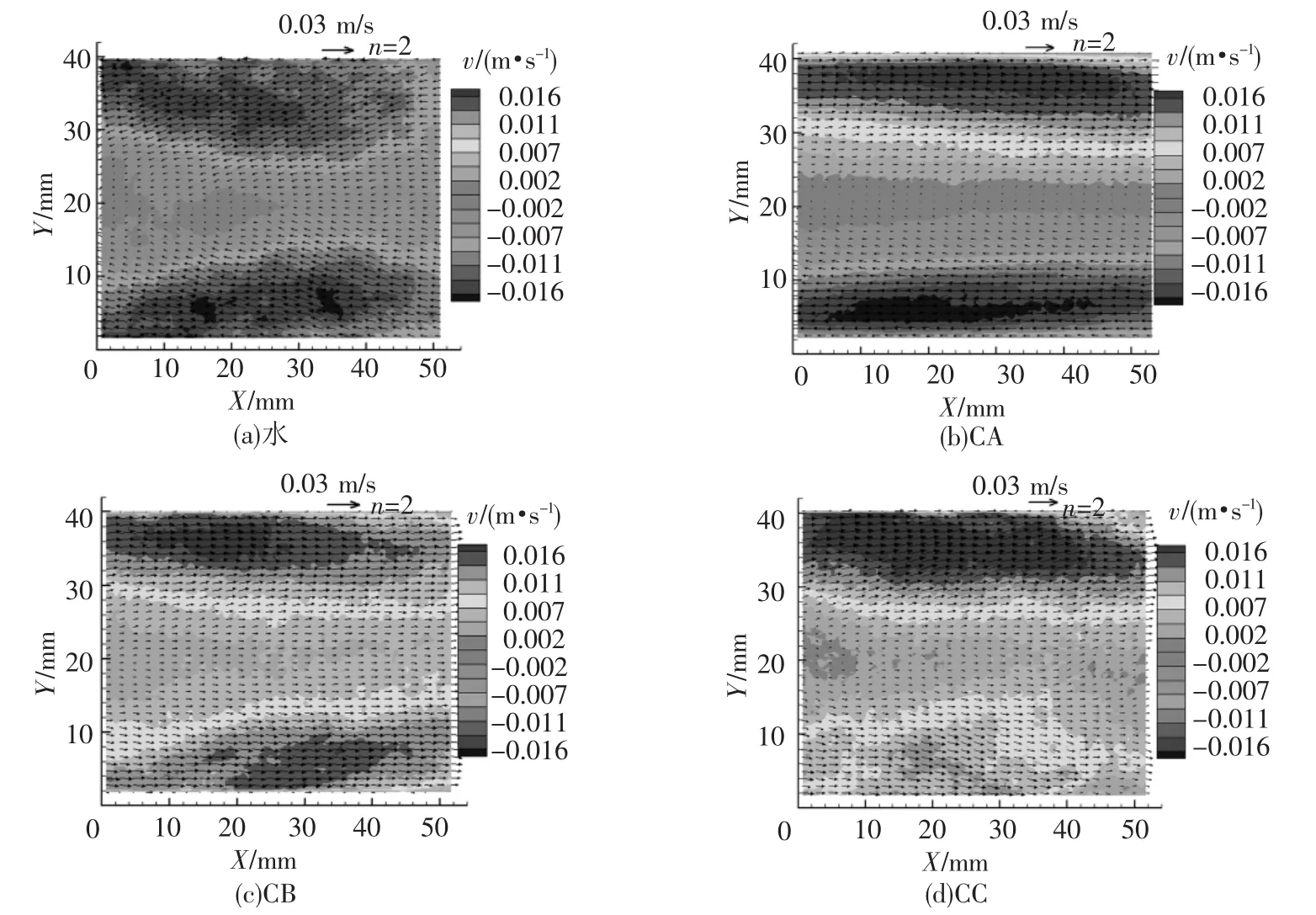
图4 水和CTAC水溶液流动中第2阶本征函数流场矢量图及流向速度云图

第3阶和第4阶流场矢量图及流向速度云图分别如图5和6所示(图中右上角处的速度为速度矢量参考值).从图中清晰可见，第3阶和第4阶本征函数均捕捉到这样的空间结构，即在槽道近壁处高速流体与低速流体相向时，促使低速流体抬升的结构以及相背时高速流体卷入的结构，这两个结构分别对应于相干结构的猝发与卷吸的过程，也是流动中产生能量损失的主要来源以及湍流形成的根源.例如:对于水，第3阶本征函数在下壁面捕捉到左侧高速流体挤压右侧低速流体使其抬升的空间结构，而第4阶本征函数则在上壁面捕捉到这样的空间结构，即左侧为低速流体，右侧为高速流体，中间卷吸入来自于中间流场区域的流体.此外，还发现在更高阶本征函数(如第5阶至第8阶)中也能在壁面附近处观测到类似的现象，但是结构越来越不规则且越来越多.同样，在CTAC水溶液流动中也观察到类似的结构，但是本征函数捕捉到结构的顺序、与壁面所成的角度、强度以及出现的位置与水流动中的相比存在明显差别:在CA流动中，高速流体和低速流体之间相互作用所致的空间结构的强度较弱，而且与壁面所成的角度明显较小，这是CTAC水溶液减阻和流动雷诺数低的缘故.这说明了CTAC的存在抑制了流动中猝发和卷吸过程，从而抑制了湍流发生的周期和强度.在CB流动中，同样存在上述结构，其强度以及结构与壁面所成的角度小于水流动中的，这主要是由CTAC水溶液的减阻效果所致，这一结果表明减阻机理在于CTAC的存在抑制了湍流猝发.在CC流动中，猝发与卷吸的过程发生的位置及与壁面所成的角度与水流动中的极为相似，但其强度较水流动中的要弱.

不同减阻区流动工况POD分析结果表明，在II区中，随着雷诺数的增加(如图1所示)，流动脉动结构变得更加不规则，当雷诺数达到ReC时，减阻达到了最大;此外对比CA和CB流动结果发现，虽然这两流动中所产生的减阻效果相差不大，但流动结构却存在明显的差异.这是因为当雷诺数增加到ReC时，CTAC剪切诱导结构(SIS)达到了所能承受的最大拉伸强度(即最强的网状结构)，最终获得了最高减阻百分比(70.0%).在III区中，当雷诺数增加到3.5×104时，流动结构极其混乱和复杂，但仍存在减阻效果，这充分说明了此流动结构还不足以完全破坏CTAC溶液中的SIS以至于减阻失效.但随着雷诺数进一步增加(如图1所示)，CTAC水溶液中的流动结构接近于水流动中的，最终导致减阻失效.因此，可以说CATC水溶液不同减阻流动区中，其流动结构存 在明显的差别，从而导致不同的减阻效果.

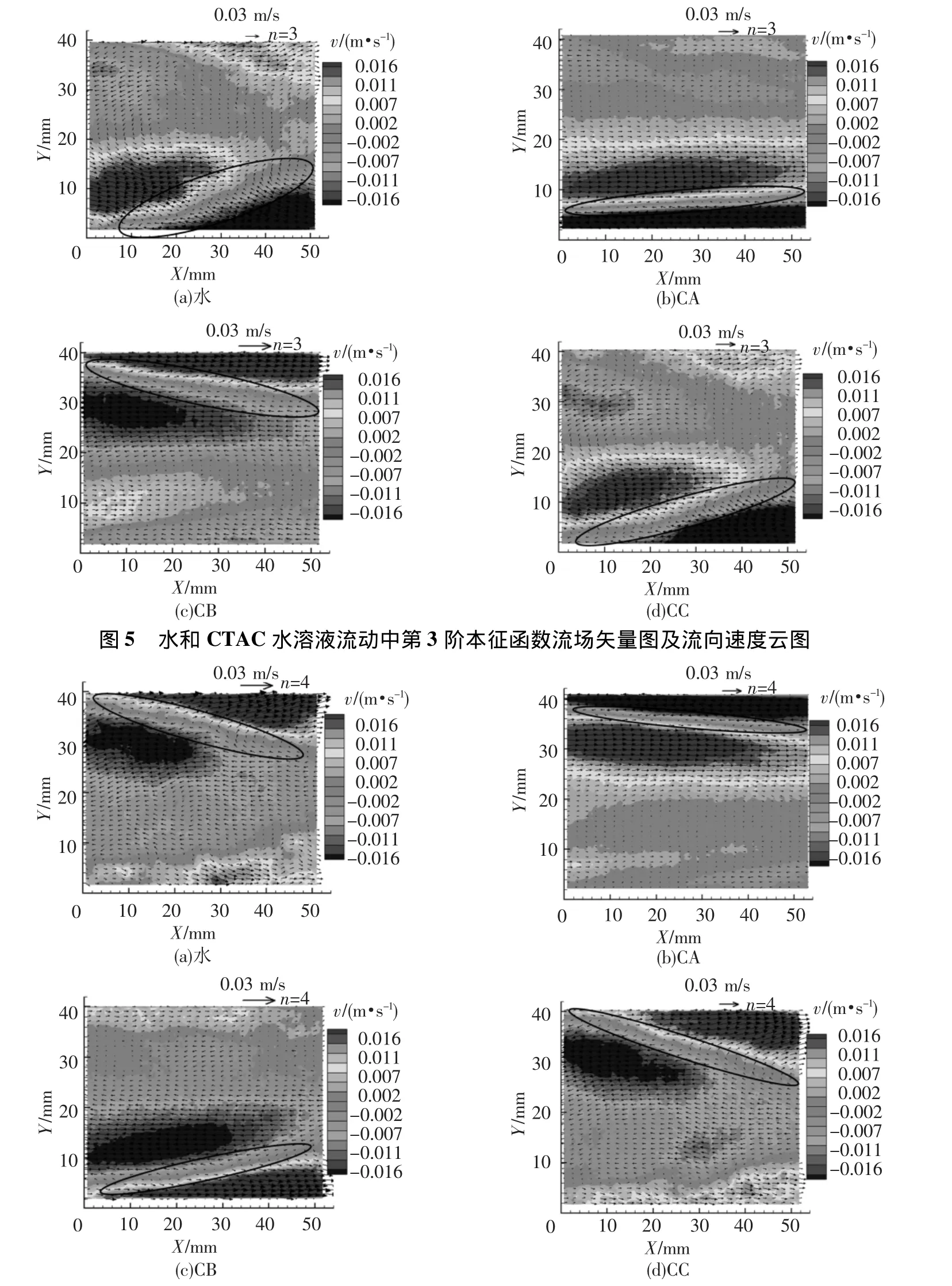
图6 水和CTAC水溶液流动中第4阶本征函数流场矢量图及流向速度云图

上述结果表明，前4阶本征函数描述了流场中主要的含能结构，随着本征函数阶数的增加，本征函数所描述的空间结构越来越复杂，空间尺度越来越小.

基于上述分析，可以得出以下重要结论:在CTAC水溶液流动中的脉动速度分布比在水中的分布更加规则，这在一定程度上解释了CTAC水溶液流动具有更小的摩擦阻力.

4 结论

1)在水、CA、CB及CC流动中，捕捉相干结构分别需要233、105、195、243阶POD本征函数.由于捕捉相干结构所需的本征函数的总阶数反映了所研究流动脉动场的复杂程度.这充分说明了CTAC的存在使流动更加规则.

2)通过前几阶含能本征函数分析，结果表明CTAC添加剂能够抑制湍流猝发的强度，从而使流动中具有更小的摩擦阻力.

3)在不同减阻流动区中，流动脉动结构存在较大差异，而且在同一减阻区中，减阻百分比相差不大的两种流动工况(CA和CB)，其流动结构却存在明显差异.

［1］TOMS B A.Some observation on the flow of linear polymer solutions through straight tubes at large Reynolds number［C］//Proceedings of the first International Congress of Rheology.North Holland:［s.n.］，1949:135－141.

［2］BEWERSDPRFF H W，OHLENDORF D.The behavior of dragreducing cationic surfactant solutions［J］.Journal of Colloid and Polymer，1988，266(10):941 －955.

［3］KAWAGUCHI Y，SEGAWA T，FENG Z P，et al.Experimental study on drag-reducing channel flow with surfactant additives-spatial structure of turbulence investigated by PIV system［J］.International Journal of Heat and Fluid Flow，2002，23(5):700－709.

［4］LI F C，KAWAGUCHI Y，SEGAWA T，et al.Reynolds-number dependence of turbulence structures in a drag-reducing surfactant solution channel flow investigated by particle image velocimetry［J］.Physics of Fluids，2005，17(7):1－13.

［5］LUMLEY J L.Drag reduction by additives［J］.Annual Review of Fluid Mechanics，1967(1):367 －384.

［6］PINHO F T，WHITELAW J H.Flow of non-newtonian fluids in a pipe［J］.Journal of Non-Newtonian Fluid Mechanics，1990，34:129 －144.

［7］TABOR M，DE GENNES P G.A cascade theory of drag reduction［J］.Europhysics Letter，1986，2(7):519 －522.

［8］LUCHIK T S，TIEDERMAN W G.Turbulent structures in low-concentration drag-reducing channel flows［J］.Journal of Fluid Mechanics，1988，190(5):241－263.

［9］WEI T，WILLMARTH W W.Modifying turbulent structure with drag-reducing polymer additives in turbulent channel flows［J］.Journal of Fluid Mechanics，1992，245:619－641.

［10］BERKOOZ G，HOLMES P，LUMLEY J L.The proper orthogonal decomposition in the analysis of turbulent flows［J］.Annual Review of Fluid Mechanics，1993，25:539－575.

［11］CHATTERJEE A.An introduction to the proper orthogonal decomposition［J］.Current Science，2000，78(7):808－817.

［12］HOLMES P，LUMLEY J L，BERKOOZ G.Turbulence，coherent structures，dynamical systems and symmetry［M］.Cambridge:Cambridge University Press，1996:26－35.

［13］DELVILLE J，UKEILEY L，CORDIER L，et al.Examination of large-scale structures in a turbulent plane mixing layer.Part 1.Proper orthogonal decomposition［J］.Journal of Fluid Mechanics，1999，391，91－122.

［14］GUNES H，RIST U.Proper orthogonal decomposition reconstruction of a transitional boundary layer with and without control［J］.Physics of Fluids，2004，16(8):2763－2784.

［15］PRABHU R D，COLLIS S S，CHANG Y.The influence of control on proper orthogonal decomposition of wallbounded turbulent flow［J］.Physics of Fluids，2001，13(2):520－537.

［16］GORDEYEV S V，THOMAS F O.Coherent structure in the turbulent planar jet.Part 1.Extraction of proper orthogonal decomposition eigenmodes and their self-similarity［J］.Journal of Fluid Mechanics，2000，414:145 －194.

［17］SAMANTA G，OXBERRY G M，BERIS A N，et al.Timeevolution K－L analysis of coherent structures based on DNS of turbulent Newtonian and viscoelastic flows［J］.Journal of Turbulence，2008，41(9):1－25.

［18］SAMANTA G，BERIS A N，HANDLER R A，et al.Velocity and conformation statistics based on reduced Karhunen-Loeve projection data from DNS of viscoelastic turbulent channel flow［J］.Journal of Non-Newtonian Fluid Mechanics，2009，160(1):55 －63.

［19］LUMLEY J L.The structure of inhomogeneous turbulent flows［C］//Atmospheric Turbulence and Radio Wave Propagation.［S.l.］:Yaglom A M and Tararsky V I，1967:166－178.

［20］SIROVICH L.Turbulence and the dynamics of coherent structures，Part I:Coherent structures［J］.Quarterly of Applied Mathematics，1987，45(10):561 －590.

［21］KAWAGUCHI Y，YU B，WEI J J，et al.Rheological characterization of drag－reducing cationic surfactant solutionshear and elongational viscosities of dilute solutions［C］//Proceedings of the Fourth ASME-JSME Joint Fluids Engineering Conference.Honolulu，Hawaii:American Society of Mechanical Engineerings，2003:721 －728.

POD analysis for the turbulent characteristics of channel flow with drag-reducing aqueous solution

CAI Wei-hua1，2，3，LI Feng-chen1，ZHANG Hong-na1，WANG Yue3，LI Xiao-bin1

(1.School of Energy Science and Engineering，Harbin Institute of Technology，Harbin，150001，China;2.School of Civil Engineering，Harbin Institute of Technology，150090 Harbin;3.School of Municipal and Environmental Engineering，Harbin Institute of Technology，150090 Harbin，China)

To investigate the turbulent drag-reducing mechanism of drag-reducing aqueous solution，turbulent drag reduction of 30×10－6cetyltrimethyl ammonium chloride(CTAC)aqueous solution in a channel flow was investigated experimentally and the influence of the drag-reducing additives on the flow structures was studied based on proper orthogonal decomposition，and POD was used to analyze turbulent fluctuating velocity based on PIV.The experimental results showed that at different Reynolds numbers，such as，1.5 ×104，2.5×104and 3.5×104，drag reduction(DR)rate of CTAC aqueous solution can reach up to 65.1%，70.0%and 33.0%respectively，and the CTAC additives can inhibit the ejection motion of low-speed fluid from the wall and sweep motion of high-speed fluid towards the wall associating with turbulent bursting events，that is to say，the CTAC additives can inhibit the formation and development of turbulent coherent structures，resulting in a great decrease of turbulent contribution to frictional drag and DR.

Drag-reducing aqueous solution;turbulent drag reduction;coherent structures;proper orthogonal decomposition(POD);particle image velocimetry

O357.1，O357.5

A

0367－6234(2012)07－0051－07

2011－07－12.

国家自然科学基金(51076036);教育部博士点基金资助项目(20112302110020);中国博士后面上基金资助项目(2011M500652);哈尔滨工业大学基础研究杰出人才培育计划项目(HIT.BRET1.2010008).

蔡伟华(1982—)，男，博士，讲师;

李凤臣(1971—)，男，教授，博士生导师.

蔡伟华，caiwh@hit.edu.cn.

(编辑 杨 波)