薄壁角接触球轴承轴向刚度分析及其实验

史士财，吴剑威，李 荣，司圣洁，刘 宏

(1.哈尔滨工业大学机器人技术与系统国家重点实验室，150001 哈尔滨;2.哈尔滨工业大学超精密光电仪器工程研究所，150001 哈尔滨;3.黑龙江工程学院汽车与交通工程学院，150050 哈尔滨)

薄壁角接触球轴承轴向刚度分析及其实验

史士财1，吴剑威2，李 荣3，司圣洁1，刘 宏1

(1.哈尔滨工业大学机器人技术与系统国家重点实验室，150001 哈尔滨;2.哈尔滨工业大学超精密光电仪器工程研究所，150001 哈尔滨;3.黑龙江工程学院汽车与交通工程学院，150050 哈尔滨)

针对薄壁角接触球轴承刚度分析中的多体接触协调变形的情况，以71718轴承为例进行了薄壁角接触球轴承的轴向刚度特性研究.根据单元大小对分析结果的影响确定合理的单元尺寸;利用所确定的单元尺寸建立71718轴承的三维有限元模型，并对其轴向刚度进行分析;搭建轴承轴向刚度测试平台，并利用该平台对71718的轴向刚度进行测试.实验结果与分析结果的对比可知，利用Hertz解析解计算时误差较大，利用有限元法得到的解与实际测试结果误差在10%以内.

薄壁轴承;有限元法;Hertz解析解;角接触球轴承;轴向刚度

近年来，随着装备制造业的发展，轻型薄壁轴承发挥着越来越重要的作用，特别在航空航天领域的应用［1］.Hertz接触理论是一个经典解，利用该理论可以解决大部分滚动轴承的应力、应变问题［2－4］.利用Hertz理论进行轴承的接触分析需要作如下几个基本假设［5］:1)接触体的材料应是匀质和各向同性;2)载荷垂直于接触表面，也就是说接触面是光滑表面，只有法向作用力，不存在切向摩擦力;3)接触体是线性弹性体，服从广义Hooke定律;4)接触面的尺寸与接触物体表面的曲率半径相比是很小的.因此Hertz理论通常用于求解接触体形状比较规整，边界条件相对比较简单的接触问题［6］.在轴向载荷作用下，薄壁角接触球轴承的轴承套圈的径向位移是不可忽略的，而基于Hertz理论的接触分析并没有考虑这些因素.随着CAE技术的发展，有限元技术被广泛应用于轴承的分析，并且具有比较高的精确度［7－9］.众所周知，合理的轴承预紧力设计不但可以提高轴承的回转精度，减小振动和噪声，还可以延长轴承的工作寿命，轴承刚度是轴承预紧力选择的一个重要依据［10－11］.

本文采用ANSYS软件对角接触球轴承71718轴向刚度进行有限元分析，设计了轴承刚度测试试验台，对71718进行轴向刚度测试，并对71718的Hertz解、ANSYS解和实验解进行了对比［12］.轴承71718 的参数为:外圈直径106 mm，内圈直径90 mm，滚珠直径3.175 mm，钢球数68个，初始接触角为25°.

1 网格密度的确定

对于静力学分析来说，网格的密度与分析结果的精确度有着直接的关系，网格过于稀疏分析结果误差会较大，如果太密会大大增大计算分析的时间.在进行轴承有限元模型建立之前应该采用一个简化的模型进行网格密度的确定，再用已经确定的网格密度去对轴承模型进行网格划分.

1.1 简化模型的建立

简化模型采用2个球体接触模型，较小尺寸的钢球直径为3.175 mm，并且与实际轴承中的钢球尺寸一致;尺寸较大钢球的直径为10 mm.载荷简化为集中力载荷，作用点在钢球顶部的中心，载荷的大小为100 N，因此可以计算0～100 N载荷作用下轴承的接触尺寸、接触应力等.钢球的材料为9Cr18不锈钢.为了减少分析时间，提高分析的效率，在ANSYS中采用轴对称的分析方法进行分析.

1.2 网格划分

在对接触球体进行网格划分时，对可能接触的部分需要进行单元尺寸的控制，采用5种不同的单元相邻节点距离进行网格划分，划分网格后的有限元模型如图1所示.

图1 有限元模型网格划分图

1.3 结果分析

对5种不同精度的有限元模型，分别计算在集中力10 N、100 N情况下的弹性趋近量、最大接触应力、接触半径等，同时利用Hertz理论求出解析解，计算结果如表1、图2和图3所示.

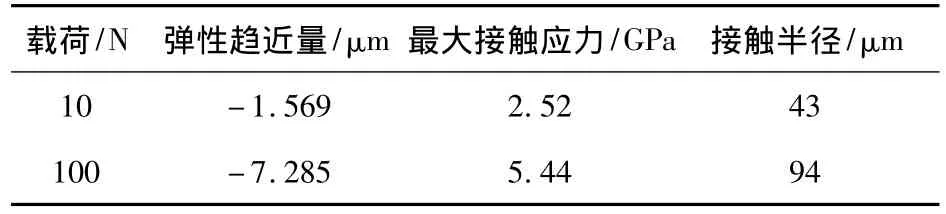
表1 载荷为10N和100N时Hertz接触分析结果

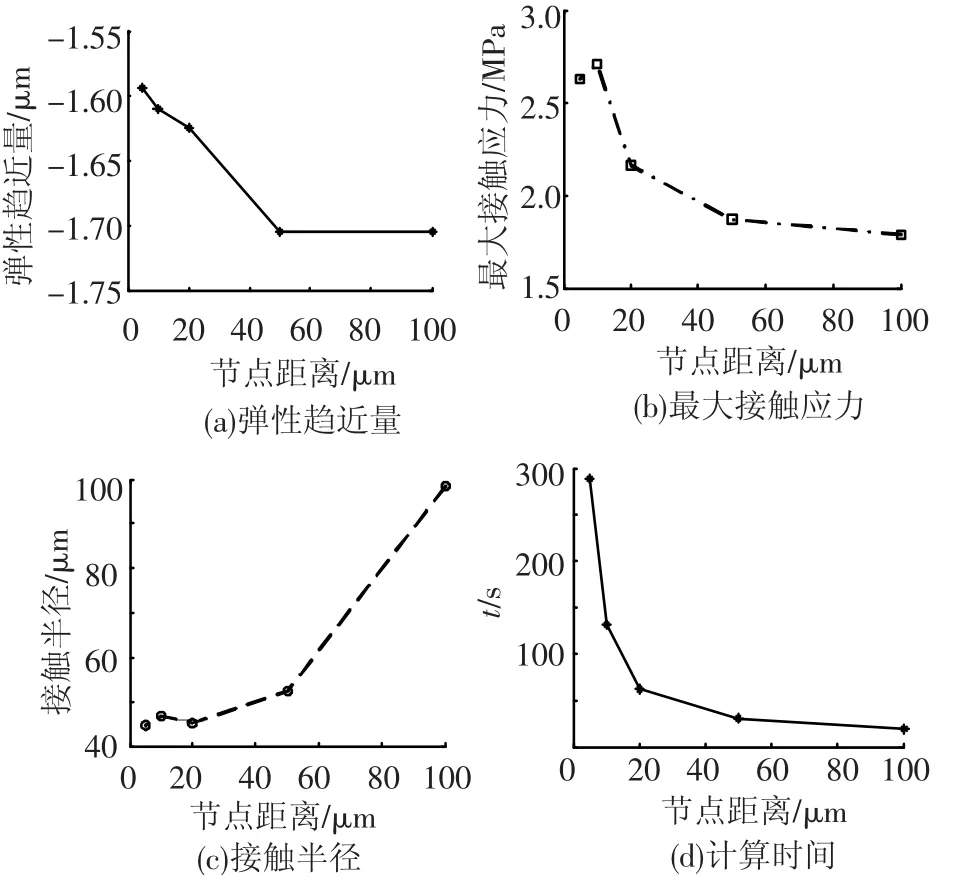
图2 载荷为10 N时ANSYS接触分析结果

图3 载荷为100 N时ANSYS接触分析结果

不同载荷作用下采用ANSYS分析得到的数值解与采用Hertz接触理论得到的解析解的对比情况如图4和图5所示.

从图4和图5可以得出以下结论:

1)网格划分精度和载荷大小对弹性趋近量的计算结果影响较大，随着网格划分密度的提高或载荷的增大，弹性趋近量的计算结果更加精确.

2)由于单元尺寸对应力的平均效应，网格划分精度对最大接触应力的计算精度存在较大影响，网格划分得越粗糙，最大接触应力的计算结果越小.但是网格划分也不能过细，如果网格划分过细也可能导致应力奇异的发生，使得计算得到的最大接触应力与实际结果相比偏大.

3)网格划分的精度直接决定了接触半径计算结果的精度.当单元节点距离大于实际接触半径时，则计算得到的接触半径尺寸的最小值将等于单元节点距离的大小，很难得到准确的计算结果.在网格划分时，单元节点距离取值越小，计算结果将会越精确;当实际接触半径是单元节点距离的整数倍时，计算结果将会更加精确.

4)网格划分精度对计算时间的影响特别显著，随着单元节点距离的减小，计算时间迅速增加;因此在实际工程计算时需要在确保计算精度的前提下，尽可能降低网格的划分精度，以提高计算效率.

由此可知，在进行实际工程分析计算之前，应先通过待分析模型的接触条件利用Hertz接触理论估算接触半径的大小，然后根据估算得到的接触半径以及求解的需求确定网格划分的精度.

通过以上分析结果可知，当单元相邻节点间距离为0.02 mm时，弹性趋近量和接触半径的ANSYS数值解与Hertz解析解的误差都在5%以内，可以满足实际工程的需要，并且计算的效率相对较高;因此在本文后续角接触球轴承的接触分析中，轴承的有限元模型中钢球与轴承套圈接触部位的单元节点距离设为0.02 mm.

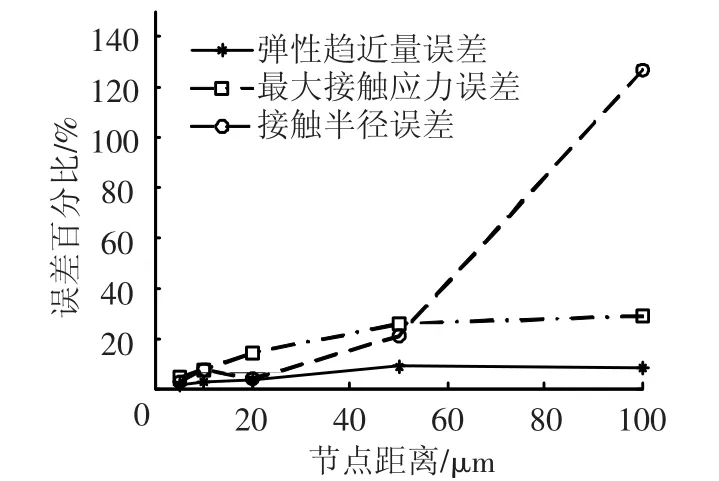
图4 10 N载荷下ANSYS数值解与Hertz解析解的对比

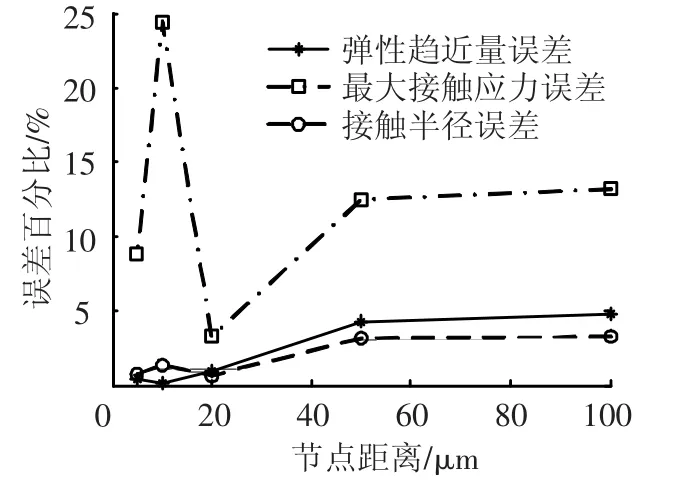
图5 100 N载荷下ANSYS数值解与Hertz解析解的对比

2 薄壁角接触球轴承的轴向刚度计算

对于工作在大温差环境下的轴系系统进行设计时，轴承内外套圈通常与相对应的轴或壳体采用间隙配合.当薄壁角接触球轴承受到轴向载荷的作用时，其内外套圈的直径尺寸将发生变化，使得工作在较大轴向载荷状态下的角接触球轴承的内部几何特征和力学特性与初始工作状态有较大的不同.由于传统Hertz接触理论分析是建立在几个理想假设基础上的，忽略了轴承套圈直径尺寸在接触分析中的变化，必然会对计算结果带来较大的误差;因此在对薄壁角接触球轴承进行有限元分析时，应充分考虑轴承内部的协调变形条件.

2.1 有限元模型的建立

为了提高程序的通用性和工作效率，本文在对71718X3角接触球轴承进行参数化建模时采用了ANSYS的程序化设计语言APDL语言.倒圆角的存在会急剧增加有限元模型的节点和单元的数量，增大计算成本;因此在对71718X3角接触球轴承进行有限元建模时删除对分析结果影响不大的倒圆角.由于71718X3轴承在工作中转速不高，在对其进行静力学分析时可忽略保持架的影响，即在有限元建模时不考虑轴承保持架.

在轴承轴向刚度的分析中设轴承只承受轴向载荷，并且轴承结构沿圆周方向呈循环对称分布结构，在ANSYS分析中可以采用循环对称分析.这样在对轴承进行有限元求解时既可以明确求解精度，也可以提高计算效率.采用循环对称分析时，通过求解一个基本扇区来构造整个环形对称结构的整体解.

2.2 网格划分

轴承的接触变形主要集中在钢球与轴承内套圈的外沟道和外套圈的内沟道的接触区域;因此在对轴承进行有限元网格划分时应将重点放在该接触区域上.根据前面的分析结果，对轴承模型进行有限元划分时，应先通过ANSYS有限元软件中的单元尺寸控制功能设定该接触区域中的单元边长尺寸为0.02 mm，然后再对整个轴承模型进行自适应网格划分.图6为划分好网格的轴承有限元模型，其中节点23 723个，单元13 759个.

2.3 接触对与边界条件的设定

ANSYS有限元软件提供了多种接触单元用于接触分析，其中TARGE170和CONTA174单元可以用来模拟3－D曲面之间的面－面接触，支持面－面之间有大的滑移［13］.在轴承的接触模型中，钢球与内、外套圈沟道的接触为曲面接触，并且当轴承的接触载荷发生变化时钢球与内、外套圈之间还会产生滑动;因此在本文的轴承接触分析中采用TARGE170单元来模拟钢球的目标面，用CONTA174单元来模拟轴承内、外套圈沟道上的接触面.

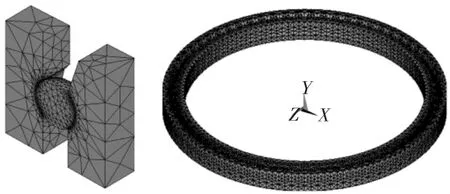
图6 71718X3角接触球轴承的有限元模型

在分析中，轴承承受最大轴向载荷为500 N，均匀施加在轴承内套圈的一个端面上.轴承外套圈的大端面的轴向自由度固定，并限制轴承内、外套圈的旋转自由度.

2.4 载荷步控制与求解

接触分析是一种高度的非线性行为，并且收敛困难.有限元接触分析收敛的快慢、收敛与否与网格划分的精度、边界条件的简化与设置、荷载步控制等因素有关.其中网格划分精度对接触分析结果的影响在前面已经做过详细讨论，而轴承的边界条件是确定的，因此合理的载荷步和时间控制是本文中轴承接触分析求解收敛的先决条件.

步长选择对收敛过程影响较大，步长过小会使得计算量过大，计算时间增加;步长过大，会使收敛过程产生突变，进而求解失败.因此需要确定合理的步长，使得收敛过程较平稳，不致于过渡振荡.在轴承的接触分析中，载荷步的结束时间与载荷的大小是相互对应的，将载荷步结束时间设为500，对应于轴向最大载荷500 N.为提高求解效率，将非线性选项中的线性搜索选项打开，同时开启大位移效应.在接触分析中，通过观察非线性分析收敛曲线可知道求解结果是否收敛以及收敛的过程.

2.5 结果分析

2.5.1 轴承位移与应力分析结果

在求解结束之后，进入通用后处理模块(POST1)，选择子载荷步进行分析，轴承的位移分析结果如图7所示.由图7(a)可以看出，轴承内、外套圈在非接触区域的变形数值很小，内套圈相对外套圈沿轴向有一个整体位移，位移大小为0.0126 mm.由图中可以看出，轴承钢球也发生了位移，并且钢球与轴承内套圈接触部位的轴向位移明显要大于钢球与轴承外套圈接触部位的位移，证明钢球在500 N的轴向载荷的作用下不仅有一个整体的轴向移动，而且还发生了转动.图7(b)为轴承等效位移的矢量图，从图中可以看出，在轴向载荷的作用下，由于轴承内、外套圈均受到了钢球的相互挤压作用，在钢球挤压载荷径向分量的作用下，内套圈直径尺寸产生了收缩，而外套圈直径尺寸发生了膨胀.

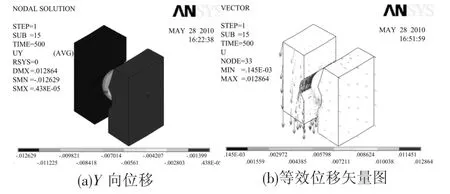
图7 轴承位移分析结果

图8为轴承的应力分析结果.从图8(a)中可以看出:轴承的应力主要集中在接触区域，在最大轴向力500 N载荷的作用下，钢球与轴承套圈的最大接触应力479.35 MPa.从图8(b)中可以看出应力深度约为0.318 mm，表层接触应力很大，随着应力深度的增加，应力迅速降低.从按路径提取的应力曲线上可以看出钢球与外套圈的接触应力大于钢球与内套圈的接触应力.

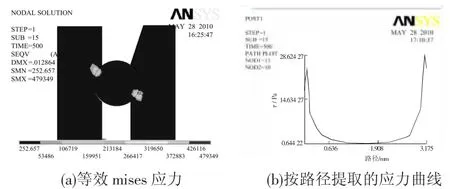
图8 轴承应力分布

2.5.2 钢球接触尺寸与应力分析结果

从图9轴承的接触状态云图中可以看出，钢球与轴承内、外套圈的接触面均为椭圆面，其椭圆率大约为7，与采用Hertz理论计算得到的结果基本相当.通过ANSYS中的列表可以得到钢球与内、外套圈的最大接触应力分别为715.51 MPa和814.94 MPa.通过单元表查询可得出钢球与轴承内、外圈的接触面积分别为0.023 25 mm2和0.024 93 mm2.从计算结果可以看出，钢球与轴承内沟道的接触面积小于钢球与轴承外沟道的接触面积.

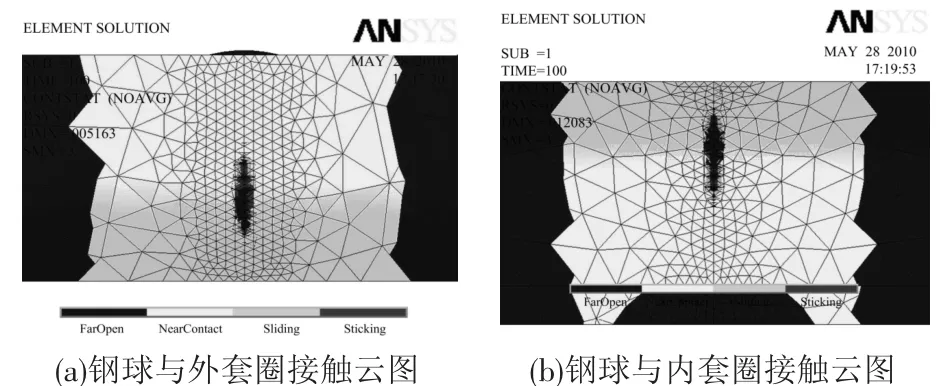
图9 轴承接触状态云图

2.5.3 轴承载荷－位移曲线

通过对轴承进行接触分析可以确定其刚度特性，根据其刚度特性来设计合适的预紧载荷.

选取一个靠近轴承内套圈下端面不受接触载荷影响的节点，利用其轴向位移来等效轴承内套圈的轴向位移.轴承的载荷位移关系如图10所示.

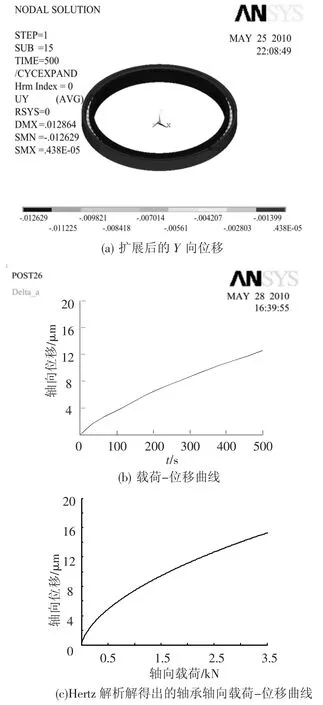
图10 轴承的载荷－位移关系

将采用ANSYS有限元分析软件计算得到的轴承载荷－位移曲线与图10(c)所示的利用Hertz解析解得到的载荷－位移曲线进行对比，可以看出:

1)轴承的轴向位移随轴向载荷的变化趋势基本相同.在起始阶段曲线的斜率较大，刚度较低，随着载荷的不断加大，刚度逐渐变高.

2)利用有限元软件计算得到的轴承轴向位移要小于利用Hertz解析解得到的轴承轴向位移.这主要是由于利用Hertz接触理论得到的解析解是建立在几个假设条件基础上得到的，它并没有考虑到薄壁轴承在间隙配合使用中内、外套圈受载时的径向尺寸变化，并且没有考虑钢球与套圈接触面之间的摩擦和滑动.

3 轴承刚度测试与分析

3.1 轴承刚度测试实验台

为了验证轴承71718X3轴向刚度计算结果的准确性，搭建了轴承轴向刚度测试平台.在测试中将轴承外套圈固定在测试平台基座的定位心轴上;通过力传感器对轴承内套圈施加沿轴向的载荷来实现加载;利用测试装置上的位移传感器对轴承内套圈的轴向位移进行检测.利用所测得的力与位移数据得到轴承的轴向载荷－位移曲线，即轴向刚度曲线.

轴承轴向刚度测试平台主要由基座、加载装置、导向装置、轴承安装工装、压力传感器、位移传感器等几部分组成.

加载装置采用弹簧加载、力传感器检测的方式.与砝码加载方式相比，采用弹簧加载的方式可以使加载载荷连续变化，并且通过采用弹簧可以对加载载荷进行细分，提高载荷的分辨率;与气动加载方式相比，弹簧加载方式更加平稳.

导向装置采用直线轴承实现.高精度的直线轴承可以抵消加载装置可能会对轴承施加附加的力矩和侧向力，保证所施加的载荷为纯轴向载荷，从而得出更加准确的测试结果.

用力传感器直接检测对轴承所施加的轴向载荷的大小，本测试平台采用的高精度S梁型测力传感器BK－2S具有精度高，性能稳定，安装使用方便等特点.

位移检测采用电感测位仪实现，测头采用旁向电感测头Mahr1318，该电感测头重复精度可以达到0.1 μm，读数采用Mahr公司的C1216电箱.

3.2 测试结果

实验测得结果与Hertz解析解以及ANSYS有限元解的对比情况如图11所示.

图12为基于Hertz理论得到的解析解与用ANSYS有限元软件得到的有限元解相对于测量值的误差曲线.从图中可以看出，在载荷较小时，Hertz解析解和测量值的误差相对较小，随着载荷的增加，其误差逐渐增大.这主要是由于随着轴向载荷的增大，轴承内外套圈所受径向载荷分量也在增加，从而导致轴承内外套圈的径向尺寸变化量也随着增大;而基于Hertz接触理论的解析解的假设忽略了这种轴承套圈的径向尺寸变化.利用ANSYS得到的有限元解与测量值相比误差较小，并且在轴向载荷超过150 N后误差维持在10%以内，随着载荷的增大，误差呈逐渐减小趋势.

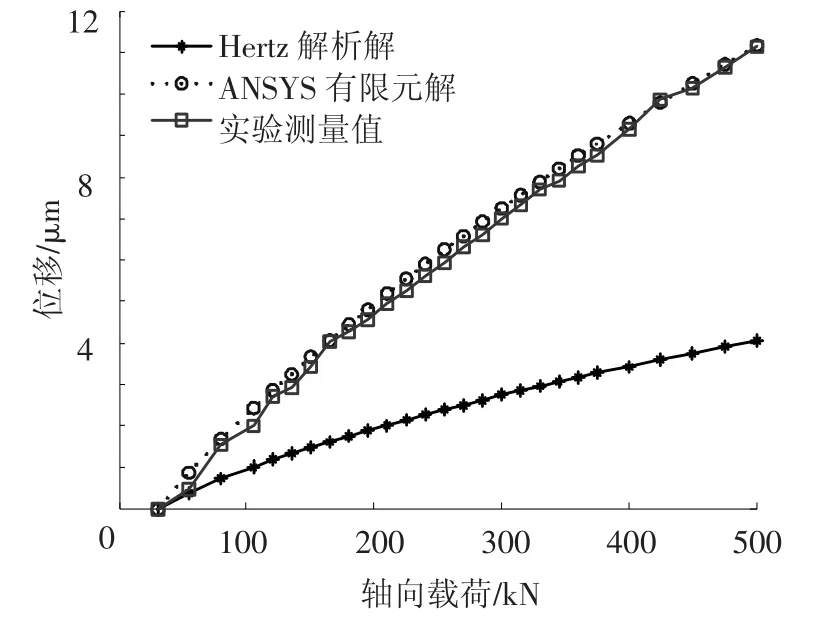
图11 轴承载荷－位移曲线

图12 Hertz解析解和ANSYS数值解的误差曲线

4 结论

1)基于Hertz接触理论的假设与71718X3角接触球轴承的工况差别较大，不适用于间隙配合的薄壁角接触球轴承的轴向刚度分析;

2)采用有限元软件ANSYS，考虑钢球与套圈沟道接触面之间的滑动和摩擦，求解得到的有限元解与测量值基本相符，并且误差在10%以内，可以满足实际工程应用的需要.

［1］KANG Y P，CHANG J W，TSAI S C，et al.Integrated CAE strategies for the design of machine tools pindlebearing systems［J］.Finite Elements in Analysis and Design，2001，37(6):485 －511.

［2］吴飞科，罗继伟，张磊，等.关于Hertz点接触理论适用范围的探讨［J］.轴承，2007(5):1－3.

［3］JONES A B.A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions ［J］.Journal of Basic Engineering，Transactions of ASME，1960，82(1):309－320.

［4］JONES A B，HARRIS T A.Analysis of arolling element idler gear bearing having a deformable outer race structure［J］.Journal of Basic Engineering，Transactions of ASME，1963，85(2):273－278.

［5］万长森.滚动轴承的分析方法［M］.北京:机械工业出版社，1987.

［6］HARRIS T A.Rolling bearing analysis［M］.New York:John wiley and Sons Inc，2001:146 －157.

［7］陈署泉，肖曙红，杨士铁.角接触球轴承的静态接触分析［J］.轴承，2009(11):4－7.

［8］倪艳光，刘万强，邓四二，等.计及套圈变形的薄壁角接触球轴承性能分析［J］.航空动力学报，2010，25(6):1432－1436.

［9］PALANISAMY R，VARONIS O J.Finit element optimization of field configuration for the eddy current testing of roller bearing rib rings［J］.Journal of Applied Physics，1988，63(8):3182－3184.

［10］王硕桂，夏源明.过盈配合量和预紧力对高速角接触球轴承刚度的影响［J］.中国科学技术大学学报，2006，36(12):1314－1320.

［11］TU J F，STEIN J L.Model error compensation and robust observer design.II.Bearing temperature and preload estimation［C］//Proceedings of the 1994 American Automatic Control Council.Baltimore，MD，USA:A-merican Automatic Control Council，1994:3308－3312.

［12］司圣洁.空间关节的轴承预紧及其动态特性研究［D］.哈尔滨:哈尔滨工业大学机电工程学院，2010.

［13］DESALVO G J，SWANSON J.A.ANSYS Users Manual［M］.Houston:Swanson Analysis Systems Inc，1991:60－72.

Axis stiffness analysis of thin-section angular contact ball bearing and its experiment

SHI Shi-cai1，WU Jian-wei2，LI Rong3，SI Sheng-jie1，LIU Hong1

(1.State Key Laboratory of Robotics and System，Harbin Institute of Technology，150001 Harbin，China;2.Institute of Ultra-precision Optical＆ Electronic Instrument Engineering，Harbin Institute of Technology，150001 Harbin，China;3.Dept.of Automobile，Heilongjiang Institute of Technology，150050 Harbin，China)

For the problem of multi-body contact and co-deformation in the stiffness analysis of angular contact thin-section ball bearings，an angular contact ball bearing 71718 is taken to investigate the axial stiffness of the thin-section bearing.Firstly，the reasonable finite element dimension is acquired based on the influence of the element dimension on the finite element analysis(FEA)results.Secondly，the finite element model of bearing 71718 is established to analyze the axial stiffness characteristics.Finally，the bearing axial stiffness test table was set up to test the axial stiffness of bearing 71718.The comparisons between test results and analysis results show that the Hertz analytical solutions has large calculation errors，the finite element results are close to real results，and the error is less than ten percent.

thin-section bearing;finite element method;Hertz analytical solution;angular contact ball bearings;axis stiffness

TH133.33

A

0367－6234(2012)07－0032－06

2011－07－03.

国家高技术研究发展计划资助项目(2006AA04Z228)，中国博士后科学基金资助(20080430131)，中国博士后科学基金特别资助(200902400)，黑龙江省博士后基金资助项目(LBH－Z07171)，机器人技术与系统国家重点实验室开放研究项目资助(SKLRS-2011-MS-08).

史士财(1978—)，男，博士，讲师;

刘 宏(1966—)，男，教授，博士生导师.

史士财，sschit@hit.edu.cn.

(编辑 杨 波)