带卡尔曼估计器的无拖曳卫星干扰补偿控制

李传江，王玉爽，马广富，张海博

(哈尔滨工业大学航天学院，150001 哈尔滨)

带卡尔曼估计器的无拖曳卫星干扰补偿控制

李传江，王玉爽，马广富，张海博

(哈尔滨工业大学航天学院，150001 哈尔滨)

为使外界干扰对无拖曳卫星的影响降低，设计了基于卡尔曼滤波的干扰估计器，对实际存在的干扰进行前馈补偿，并基于二次型最优指标设计了最优控制器.首先建立了无拖曳系统位移模式下卫星与质量块的相对轨道动力学模型，然后给出了无拖曳卫星状态估计的过程，并根据估计得出的状态设计了最优控制器，最后在卡尔曼滤波的基础上，根据得到的估计干扰对实际干扰进行补偿，组成带有前馈回路的控制系统，利用MATLAB/Simulink软件进行仿真.仿真结果表明，带有干扰补偿的最优控制器能对外界干扰进行有效地抑制，从而满足了无拖曳卫星的控制精度要求.

无拖曳卫星;卡尔曼估计器;最优控制;干扰补偿

1959 年 George Pugh［1］首次提出了无拖曳卫星的概念，1964年 B Lange［2］在其博士论文中详细论述了无拖曳卫星模型及控制器设计.无拖曳卫星由外部的卫星本体和内部的质量块组成，卫星上装有位置传感器和微推力器，其中位置传感器精确测量卫星本体与质量块之间的相对位置，并反馈给推力器，通过此反馈系统，卫星不断跟踪质量块，防止与质量块接触，使质量块悬浮于卫星的中心.内部的质量块可以看作1个理想的稳定参考源，在优化控制算法的作用下，通过高精度传感器和执行机构的配合，卫星本体通过跟踪质量块也能实现较高的稳定度，从而可搭建出1个满足低干扰要求的平台.

无拖曳卫星控制技术对于空间基础科学研究、高精度微重力实验、对地观测和深空探测具有重要意义.目前已经成功发射的无拖曳卫星有:1972年美国的TRIAD I、2004年美国的GP-B以及2009年欧洲的GOCE.还有一些计划中的卫星，如美欧合作的LISA、美国的STEP、法国的MI-CROSCOPE、意大利的Galileo Galilei以及中国南京紫金山天文台的ASTROD.

无拖曳卫星控制系统的目标是使卫星上的非重力加速度达到最小，由于内部质量块几乎运行在纯重力轨道上，因此通过控制卫星跟踪质量块可以达到这一目标.卫星和质量块的状态可以通过直接测量得到或者由1个观测器决定，对于后一种方法而言，观测器的输出——估计的状态量反馈给控制器，通过闭环控制使卫星达到期望的状态［3］，无拖曳控制系统结构图如图1所示.

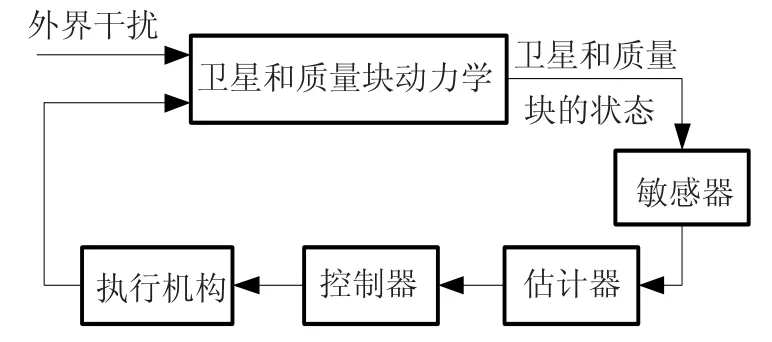
图1 含有估计器的无拖曳控制系统结构

然而对于实际系统而言，必然存在着诸如过程噪声和量测噪声等各种各样的噪声，已不再适合采用确定性系统的状态观测器理论.针对GOCE卫星，文献［4］采用了两种不同的估计模型，对线性连续系统的状态估计问题进行了研究，文献［5］在离散时间模型的基础上，设计了内嵌模型控制器，其中闭环状态估计器包含内嵌模型和噪声估计器两部分.针对STEP卫星，文献［6］研究了状态估计和参数估计问题.

在轨运行的无拖曳卫星会受到大气阻力、太阳光压等外部干扰的影响，通常这些外部干扰为常值或是可建模的，通过对外部干扰进行建模和估计，在此基础上加入前馈控制，可以将估计值直接反馈从而对外部干扰进行补偿.

本文采用了卡尔曼滤波器对无拖曳卫星的状态及外部干扰进行估计，设计最优控制器并利用估计得到的干扰对控制系统进行补偿，从而满足了控制系统的精度要求.

1 无拖曳卫星相对动力学模型

加速度计模式(AM)和位移模式(DM)是无拖曳卫星的两种主要工作方式.位移模式为卫星本体跟踪质量块，直接实现无拖曳;而加速度计模式为质量块跟踪卫星本体，再根据加速度计的输出控制卫星本体实现无拖曳.本文的目的是研究位移模式下无拖曳卫星控制系统的设计，采用位移模式最主要的优点是系统控制精度高，因为使质量块悬浮不需要力或只需要很小的力，从而使噪声水平很低［7］.考虑外部的卫星和内部的质量块为两个分开的刚体，各自运行在轨道上，且受到外力的作用.为了控制卫星跟踪质量块，需要测量卫星和质量块的相对位置，必须考虑耦合的卫星－质量块动力学.为推导运动方程所需的参考坐标系如图2所示.

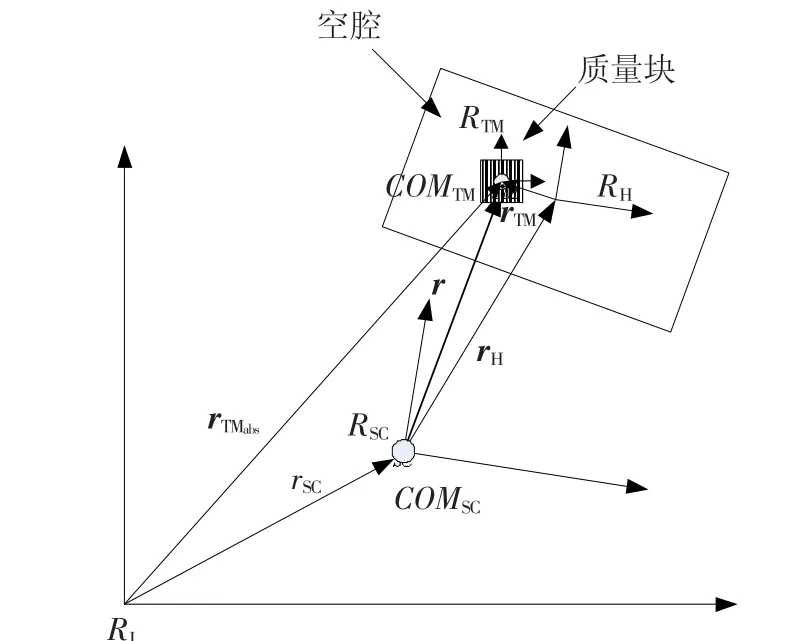
图2 无拖曳卫星参考坐标系

图中，RI为惯性参考坐标系;RSC为卫星本体坐标系，原点为卫星的质心;RH为空腔本体坐标系，原点为卫星的无拖曳点，也即空腔的中心位置;RTM为质量块本体坐标系，原点为质量块的质心，坐标轴和质量块的惯性主轴平行;rSC为卫星的质心在惯性系的位置矢量;rTMabs为质量块的质心在惯性系的位置矢量;rH为空腔中心相对于卫星质心的距离，对于位移模式的无拖曳卫星来说，空腔中心与卫星质心重合，即rH=0;r为质量块质心相对卫星质心的位置矢量;rTM为质量块质心相对空腔中心的位置.

假设无拖曳卫星只包含1个质量块，质量块采用静电悬浮的方式.通过卫星本体和质量块各自的轨道动力学模型，得到质量块和卫星本体的相对动力学线性化模型为

其中:mSC为卫星的质量;mTM为质量块的质量;vTM为质量块相对于空腔坐标系速度矢量;rTM可由敏感器测量得到，有

feSC为作用在卫星上的外力之和，包括控制力fcSC和干扰力fdSC;feTM为作用在质量块上的外力之和，本文中质量块受到的外力只考虑质量块与卫星本体间的耦合力，则

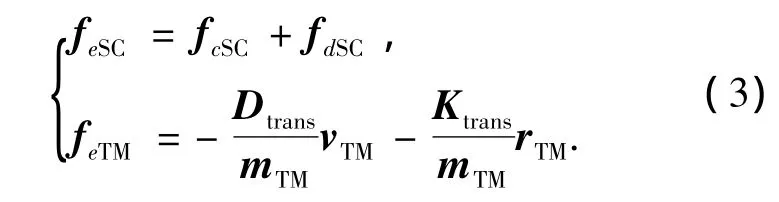
式中Dtrans和Ktrans为卫星本体与质量块的耦合系数矩阵.轨道坐标系的原点选为质量块的质心，ω0为轨道角速度ω0=［0 0 ω0］T，假设无拖曳卫星运行在圆形轨道上，轨道半径为rSC=a，则

其中

式中03和I3分别表示3×3的零矩阵和3维单位矩阵.

2 无拖曳卫星内外干扰分析

无拖曳卫星受到的主要干扰力包括:大气阻力、太阳光压以及与质量块之间的相互吸引力等.对于近地轨道卫星，气动力是主要的干扰，对于深空探测卫星，太阳光压是主要干扰.表1中给出了无拖曳卫星在近地轨道上(＜500 km)所受摄动力的模型及参数.

表1 卫星所受的摄动力模型及参数

除外部干扰外，系统上常作用有各种噪声，如系统噪声和敏感器的量测噪声等.卫星受到的噪声和干扰都是随机信号，可以利用功率谱密度进行描述.图3给出了卫星本体X轴向所受大气阻力的加速度功率谱密度曲线.

作用在卫星上的干扰力设为正余弦函数形式，可以采用式(4)所示的干扰力模型进行卡尔曼滤波器设计，

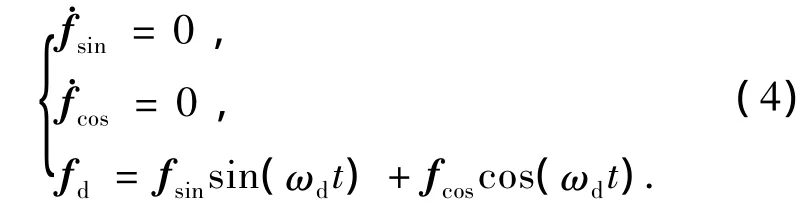
其中:fd为干扰力矢量;fsin和sin分别为干扰的正弦系数及它对时间的导数;fcos和˙fcos分别为干扰的余弦系数及它对时间的导数;ωd表示气动干扰的频率.

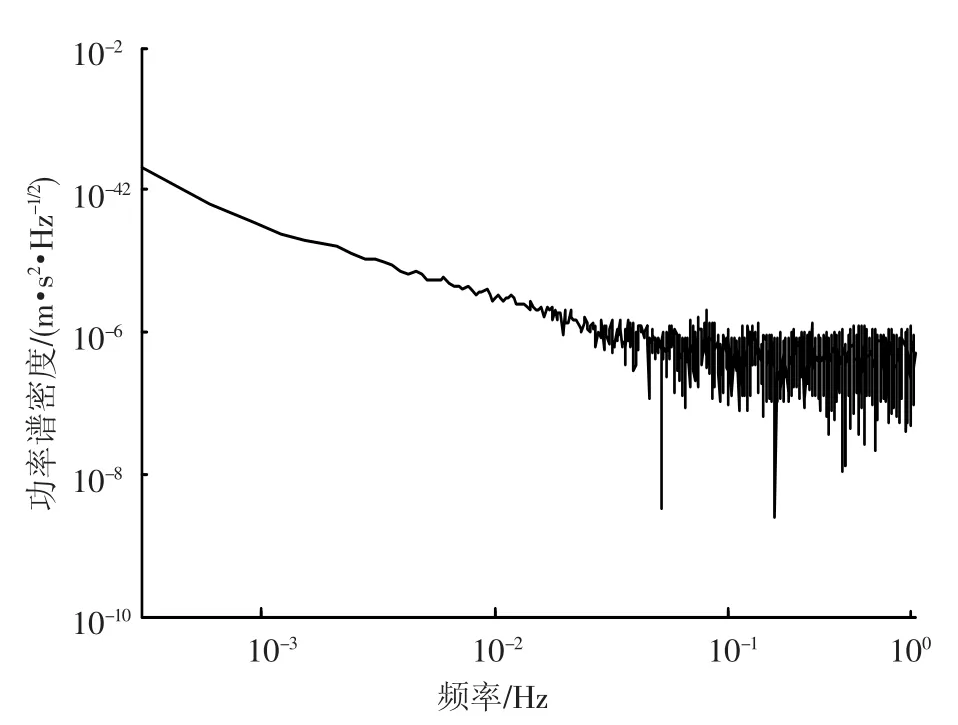
图3 大气阻力加速度功率谱密度

无拖曳控制的性能指标要求通常为在一定的测量频带内(通常是低频段)，使卫星本体和质量块上的非重力加速度噪声的功率谱密度低于某一水平［8］.本文控制指标要求如下:在 0.005～0.1 Hz的频带内，卫星本体与质量块的相对位置控制精度达到2.5×10－5m，卫星本体和质量块上的残余加速度功率谱密度分别小于2.5×10－7(m·s－2)/和2.5 ×10－9(m·s－2)/

3 最优状态估计器

对于实际的无拖曳卫星控制系统，需要考虑系统模型误差、干扰及噪声等问题，对于这样的随机系统，需要应用卡尔曼滤波理论对状态进行最优估计.

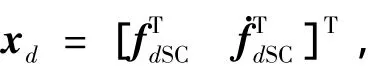
分别建立系统方程和量测方程，考虑如下无拖曳系统的状态估计问题:

其中系统的输出y(t)=C¯x(t)+Du(t);w(t)与v(t)为零均值的高斯分布噪声，分别表示过程中的干扰和输出变量量测的随机干扰，协方差矩阵为

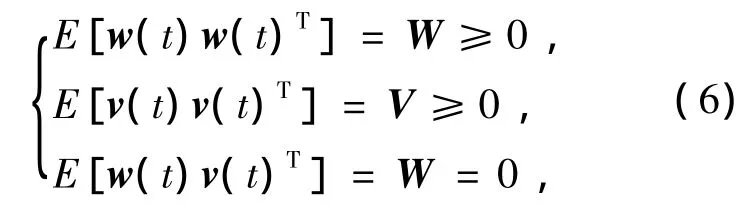
设卫星受到的干扰力具有正弦特性如式(7)所示，且在实际仿真时加入一定随机干扰:

则在式(5)中有

矩阵对(¯A，¯B)和(¯A，C)分别是能控和能观测的，根据连续时不变系统卡尔曼估计理论［9］，估计模型可以写成如下形式:

估计器增益L必须能提供在存在噪声w(t)和v(t)条件下的最佳估计.

定义估计误差

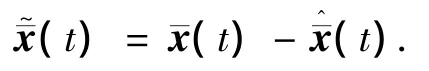
根据式(5)和式(8)推导出误差的动态方程

其中L=¯PCTV－1满足下面的代数Riccati方程:

对于卡尔曼滤波，w(t)包括了系统的干扰和模型的不确定性，v(t)则考虑了所有测量噪声和测量的不确定性，测量噪声的协方差矩阵和系统状态初值的统计特性参数可以通过观测和分析得到.

4 控制器的设计

在最优状态估计基础上，以估计状态代替系统的真实状态进行线性反馈.依据观测误差最小的原则，定义如下状态控制器的最优控制目标函数:

其中加权矩阵Q为对称半正定矩阵，R为对称正定矩阵，即Q=QT≥0，R=RT＞ 0.

易判断系统(4)可控，由最优控制理论［10］，得出存在最优控制律u*(t)使系统能够渐近稳定，并且具有满意的动态性能，控制器如下:

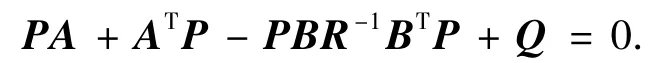
对于线性定常系统，加权矩阵Q和R均取为对称正定矩阵.

图4给出了带干扰前馈的无拖曳控制系统框图.其中，在卡尔曼滤波器中引入了干扰模型，对干扰进行估计，以补偿外部干扰引起的输出误差，卡尔曼滤波器估计得到的相对状态信息反馈到最优控制器，并在闭环系统中增加了前馈补偿控制，则作用到无拖曳卫星系统的控制力为u(t)=

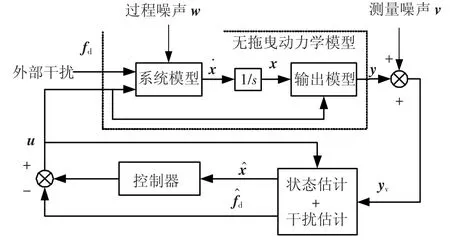
图4 具有干扰前馈的无拖曳控制系统

5 仿真分析

在Matlab/Simulink环境下进行了仿真，验证设计的控制器和加入干扰补偿后系统对干扰的抑制作用，仿真参数如下:

1)仿真的初始条件选取为:卫星本体质量为1 050 kg，质量块质量为1 kg，卫星本体和质量块之间三轴初始相对距离分别为1×10－3，5×10－3和2×10－3m.卫星本体和质量块之间的耦合系数矩阵为

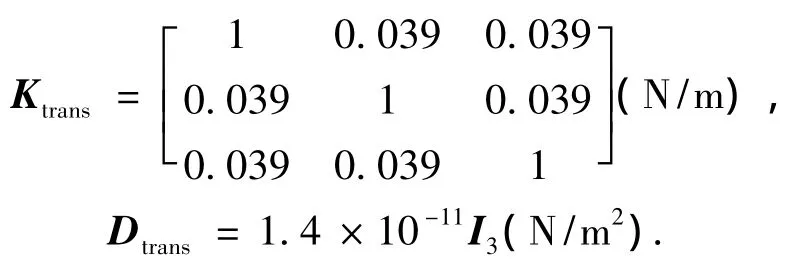
2)气动干扰的频率 ωd=1.2×10－3Hz.系统噪声和量测噪声的功率谱密度分别为

仿真结果如图5～图11所示.图5和图6分别为卡尔曼估计器对无拖曳控制系统的相对位置估计误差和相对速度估计误差.从图中可以看出，状态的估计误差大约为2×10－8.图7为干扰的估计误差曲线，估计误差大约为2×10－6.较小的估计误差表明所设计的卡尔曼滤波器能对相对位置、相对速度和外界干扰信息进行较准确地估计，估计器的性能良好.因此对于工程实际来说，良好的状态和干扰估计是很有必要的.

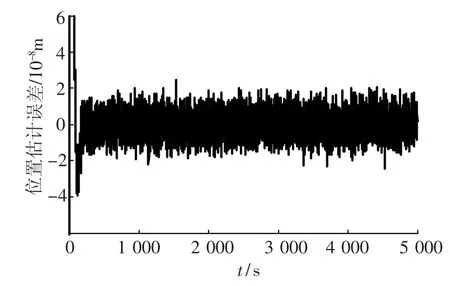
图5 X轴向相对位置估计误差

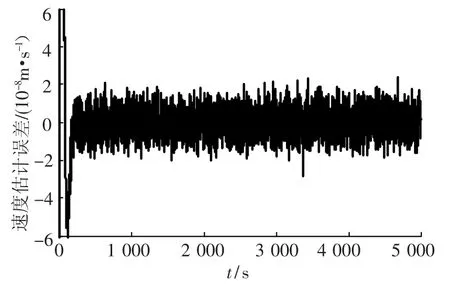
图6 X轴向相对速度估计误差

图8和图9分别为加入干扰补偿前后卫星本体和质量块的相对位置曲线.可以看出，无干扰补偿时，在干扰力的影响下，相对位置正弦运动的幅度较大.加入干扰补偿后，输出曲线变的“平缓”.在图8中相对位置的稳态值之所以是等幅振荡的正弦过程，是由于系统受外界正弦干扰的影响，因此采用经典最优控制的无限时间二次型性能指标具有一定的局限性，为了解决这一问题，可以考虑选择一种能保证收敛的最优控制的性能指标，并寻求使性能指标取得最小值意义下的最优控制律.

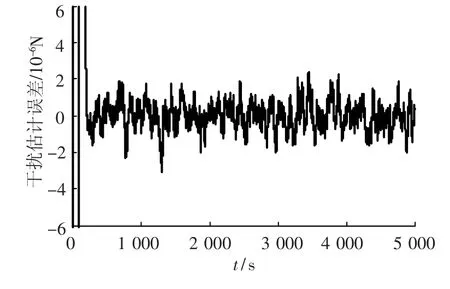
图7 X轴向干扰估计误差

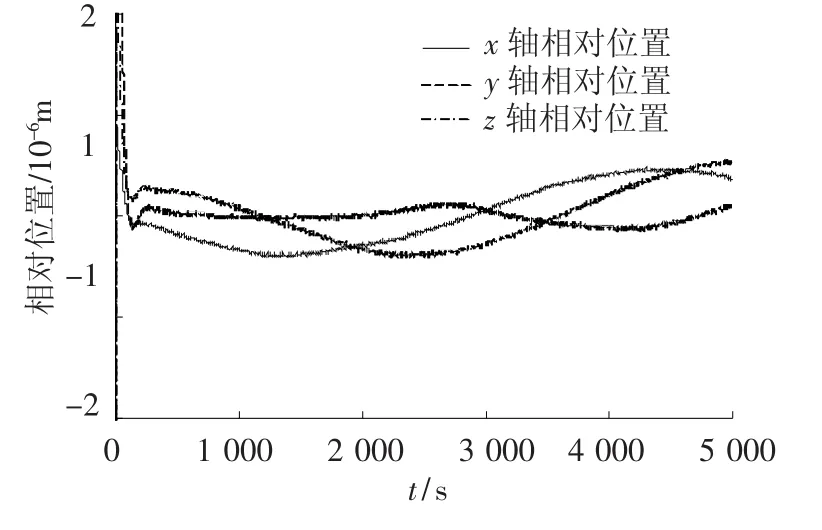
图8 干扰补偿前卫星本体和质量块的相对位置

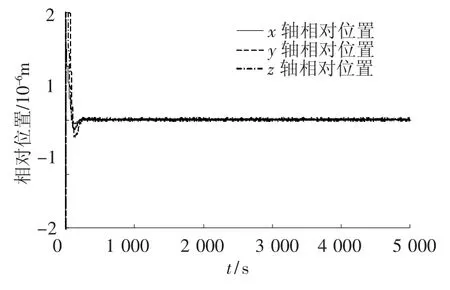
图9 干扰补偿后卫星本体和质量块的相对位置

在仿真中，只对质量块施加耦合力，控制器控制卫星本体跟踪质量块实现无拖曳控制，卫星本体和质量块上的残余加速度功率谱密度曲线如图10和图11所示.在0.005～0.1 Hz的测量频带内，卫星本体和质量块上的残余加速度功率谱密度达到了性能指标要求.

图10 卫星本体上的残余加速度功率谱密度

图11 质量块上的残余加速度功率谱密度

6 结论

本文针对存在干扰及噪声的无拖曳卫星控制系统，采用卡尔曼滤波方法对状态和干扰进行了估计，并基于状态估计设计了最优控制器，利用干扰估计采用前馈控制对干扰进行补偿，从而有效地抑制了干扰对控制系统的影响.

与传统卫星控制系统相比，无拖曳卫星对控制系统提出了极高的性能指标要求，因此，下一步将对卫星模型的建立和控制器的设计进行更深入地研究.另外，无拖曳卫星的性能指标是在频域中给出的，下一步也可以考虑基于频域的控制器设计方法，以满足控制系统的高精度及强鲁棒性要求.

［1］PUGH G.Proposal for a satellite test of the coriolis prediction of general relativity［R］.Washington DC:Weapons Systems Evaluation Group Research Memorandum，NASA，USA，1959:414－426.

［2］LANGE B.The control and use of drag-free satellites［D］.California:Stanford University，1964:55－85.

［3］党朝辉，项军华，曾国强.基于大气阻力实时辨识的Drag-free卫星最优控制研究［J］.上海航天，2010，27(6):6－10.

［4］EVERS W.GOCE Dynamical analysis and drag-free mode control［R］.Eindhoven:Eindhoven University of Technology，2004:29－35.

［5］CANUTO E.Drag-free control of the GOCE satellite:noise and observer design［J］.IEEE Transactions on Control System Technology，2010，18(2):501－509.

［6］THEIL S.Satellite and test mass dynamics modeling and observation for drag-free satellite control of the STEP mission［D］.Bremen:University of Bremen，2002:51－116.

［7］GUILHERME M S，LEITE F W C，THEIL S.Strategies for in-orbit calibration of drag-free control systems［J］.Aerospace Science and Technology，2008，12(5):365－375.

［8］DITTUS H，LAMMERZAHL C，TURYSHEV S.Lasers，clocks，and drag-free:exploration of relativistic gravity in space［M］.Berlin:Springer，2008:45 －363.

［9］GELB A.Applied optimal estimation［M］.Cambridge，MA:MIT Press，1999:119 －126.

［10］胡寿松，王执铨，胡维礼.最优控制理论与系统［M］.北京:科学出版社，2005:310－316.

Disturbance compensation control for drag-free satellite with Kalman estimator

LI Chuan-jiang，WANG Yu-shuang，MA Guang-fu，ZHANG Hai-bo

(School of Astronautics，Harbin Institute of Technology，150001 Harbin，China)

In order to reduce the influence of disturbance on the drag-free satellite，a disturbance compensation control combined with optimal control of quadratic performance based on a Kalman estimation theory is presented.Firstly，the relative dynamics of the satellite and the proof mass are modeled.Secondly，the state estimation of the drag-free satellite is given and an optimal controller is established.Finally，the control system with a feedforward loop for disturbance compensation based on Kalman filter is constructed.The simulation results in MATLAB/Simulink indicate that the disturbance compensation together with optimal control is effective to reject external disturbance，the accuracy of the drag-free satellite can be satisfied.

drag-free satellite;kalman estimator;optimal control;disturbance compensation

V448.2

A

0367－6234(2012)07－0008－06

2011－03－31.

国家自然科学基金资助项目(61004072)，中央高校基本科研业务费专项基金资助项目(HIT.KLOF.2010016)，哈尔滨市科技创新人才研究专项资金资助项目(2010RFQXG029).

李传江(1978—)，男，副教授，硕士生导师;

马广富(1963—)男，教授，博士生导师.

李传江，chuanjiangli@gmail.com.

(编辑 张 宏)