火星着陆任务落点误差快速分析方法

任高峰，朱圣英

(1.哈尔滨工业大学航天学院，150080 哈尔滨;2.北京理工大学宇航学院，100081 北京)

火星着陆任务落点误差快速分析方法

任高峰1，朱圣英2

(1.哈尔滨工业大学航天学院，150080 哈尔滨;2.北京理工大学宇航学院，100081 北京)

在火星着陆任务设计中，为高效地评估进入点导航误差等动力学方程中的不确定因素对着陆精度的影响，引入Galerkin投影法则，提出一种火星着陆落点不确定度快速预报与分析方法.该方法采用Wiener-Askey正交多项式逼近着陆器状态，将落点误差的预报问题转换为1个确定性微分方程的求解问题.最后以我国未来实施火星着陆探测为背景，分别用本文算法和蒙特卡洛方法进行数值仿真分析，结果表明，本文算法能够对落点偏差进行快速分析，准确预测其均值和方差，且计算效率明显提高.

落点误差;正交多项式;火星着陆;Galerkin投影

对于未来的火星探测任务，为了提高科学回报和降低任务成本，选择在科学价值高、地形复杂的区域进行着陆成为1个必然的要求和发展趋势［1］.然而，探测器在火星大气进入点处的导航控制误差，探测器的气动参数以及火星大气模型的不确定性，都会严重影响着陆器最终的着陆精度，甚至关乎任务的成败［2］.因此，分析这些偏差以及不确定性对着陆点的影响，是1项必不可少的工作;另外，随着着陆精度要求的提高，在设计着陆器进入大气的标称轨迹时，同时考虑了不确定性因素影响的鲁棒标称轨迹设计，成为未来标称轨迹设计发展的1个重要方向，而不确定性输入在系统中如何演化，是鲁棒轨迹规划的重要研究内容［3］.综上可见，针对火星着陆任务，发展一种快速的落点不确定度分析方法，对降低未来火星着陆设计周期和成本，提高设计效率很有意义.

对于动力学系统中不确定性的传播问题，目前存在的方法主要有蒙特卡洛仿真方法、线性化方法、无味变换方法以及Galerkin投影法等.文献［4］对蒙特卡洛方法进行了详细的阐述，这种方法的优点在于计算实施简单，可以精确得到状态量精确的统计特性，不足之处在于它的收敛速度比较慢;针对特定的问题，文献［5］提出了准蒙特卡洛方法，文献［6］提出了马尔科夫链蒙特卡洛方法，从一定程度上提高了计算效率;针对不确定性输入为高斯白噪声，动力学系统非线性强度在可接受范围内的情况，文献［7］利用线性化的方法将非线性系统泰勒展开，以线性理论为基础，以误差方差阵为表现形式，实现不确定性的递推.文献［8］提出一种确定的取样方法，利用一系列sigma点来逼近系统输入的概率分布密度，然后将非线性系统作用于sigma点，利用转换后的点来近似系统输出的统计特性，所取sigma点个数会随着系统维数及精度要求的提高而迅速增加.Galerkin投影法以混沌多项式展开为基础，因其具有严密的数学理论体系，成为目前研究的1个热点，在随机流体力学［9］，随机有限元分析［10］，固体力学［11］，空间技术［12］等领域得到了应用，但其在动力学控制与动态估计中应用很少.

本文基于Galerkin投影法，对火星着陆系统落点偏差分析问题进行了研究.首先对火星着陆器动力学系统及不确定参数进行描述，然后利用Wiener-Askey正交多项式表示着陆器的状态和不确定参数，根据Galerkin投影法则，将随机动力学系统转化为1个高维的确定性系统，最后采用牛顿积分求解正交多项式的时变系数，进一步得到着陆器状态的均值和方差.

1 问题描述

忽略火星自转，假设火星表面大气相对于火星静止，则火星着陆纵向动力学可以描述为

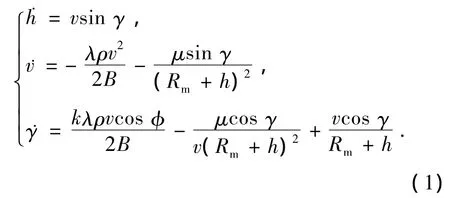
其中:h表示着陆器距离火星表面的距离;v表示着陆器速度的大小;γ表示航迹角;μ表示火星引力系数;Rm表示火星半径;B表示着陆器的弹道系数;k表示着陆器的升阻比;φ表示倾侧角;λ表示大气模型不确定性因子;ρ表示火星大气密度，其与着陆器距离火星表面高度的关系如式(2)所示，它是根据NASA开发的火星大气模型Mars-Gram所生成的数据进行最小二乘拟合得到的［3］.

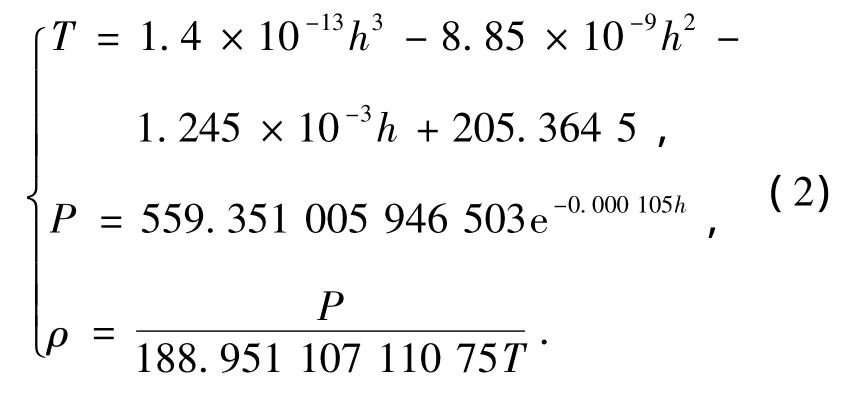
由于测控能力的限制，着陆器在进入点处的位置、速度等状态不能精确已知，并且着陆器的气动参数依靠地面试验也不能够精确建模.对应的，本文假设上述动力学方程中的状态初值和系统参数均存在不确定性，表示为

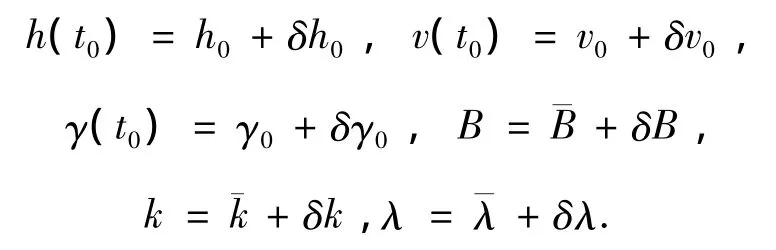
其中 δh0、δv0、δγ0、δB、δk、δλ 为符合一定分布的随机量.

根据以上描述，火星着陆系统落点偏差的分析问题可以抽象成为在初始状态和系统参数均存在不确定性的随机微分方程的求解问题.下面将利用随机投影法对上述问题进行求解.

2 Galerkin投影法

2.1 Galerkin投影法概述

Galerkin 投影法首先由 Wiener［13］提出，用于对符合高斯分布的随机过程进行建模分析;学者修东斌和 Karniadakis［14］利用 Askey正交多项式体系以及Cameron Martin定理将其推广到符合多种分布的随机过程，并对这一推广的收敛性进行了证明;随后这种方法在众多领域得到了广泛的应用［9－12］.本文利用上述成果，将带有不确定性的着陆器状态用一组正交多项式逼近，此多项式的自变量为符合一定分布的随机变量;随后将多项式表示的状态带入动力学方程中，形成1个显式表达的随机微分方程，最后利用Galerkin投影法则，将其转换为1个高维的确定性微分方程，进而通过对此确定性微分方程求解实现对着陆器状态不确定性进行分析.

2.2 Askey正交多项式体系

根据Cameron Martin定理及其推广，任何二阶随机过程X(t)可以用式(3)在L2意义上进行近似逼近:

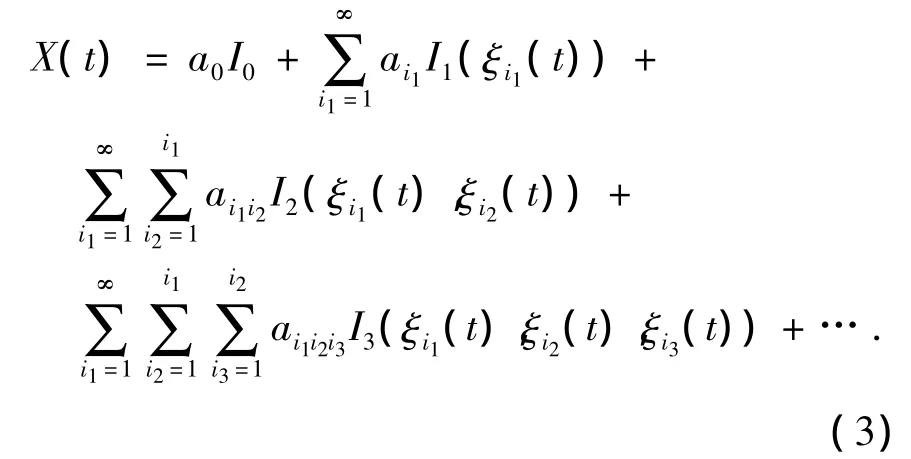
其中In是以随机变量ξ为自变量的n阶混沌多项式，为表示及后续计算方便，上式可以重新表示为以下形式:

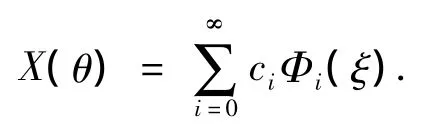
其中 Φi(ξ)与 In(ξi1(θ)，…，ξi3(θ))存在一一映射关系.

Wiener Askey混沌多项式存在以下正交关系:

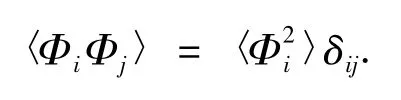
其中δij为克罗内克δ函数，并且〈·，·〉表示整体内积，假设W(ξ)为对应正交多项式的权重函数，对应于连续随机变量和离散随机变量，整体内积可以分别定义为

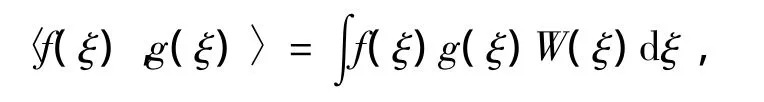
或者

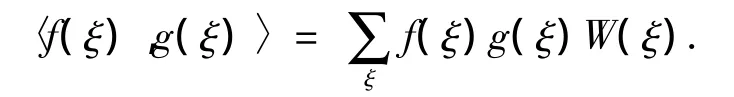
需要特别指出的是，当权重函数对应于某一随机变量的概率密度函数时，则此随机变量可以用对应于相应权重函数的一阶正交多项式精确表示.并且，对应于常用的随机变量分布类型，如高斯分布等，与一些正交多项式存在着一一对应关系，如表1所示.

表1 正交多项式与随机变量类型之间对应关系

2.3 高维确定性微分方程

利用Askey混沌多项式将式(1)～(2)描述的随机微分方程转换为确定性微分方程，首先要解决的问题是将系统的不确定性输入用混沌多项式表示，由于系统的不确定性参数(弹道系数B，升阻比k，以及火星大气不确定性因子λ)只与任务实施前对着陆器气动特性及火星大气的认知程度有关，在整个着陆过程中统计特性并不改变，本文假设这些不确定参数符合高斯分布，则可以用一阶Hermite正交多项式表示为

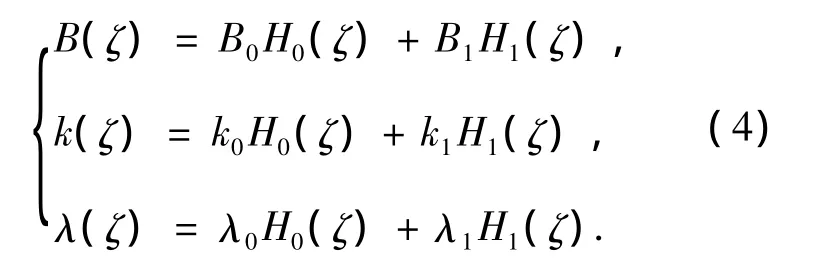
对于系统的状态(高度h、速度v以及航迹角γ)，在初始时刻通常以高斯分布的形式给出，但在着陆过程中，这些状态量之间相互影响，并且受不确定参数的影响，在着陆器着陆过程中，状态量的统计特性随时间发生变化，对于每一时刻，系统状态对应的随机变量可以用混沌多项式表示，因此对于整个时间序列中的系统状态，可以利用带有时变系数的P阶正交多项式表示:

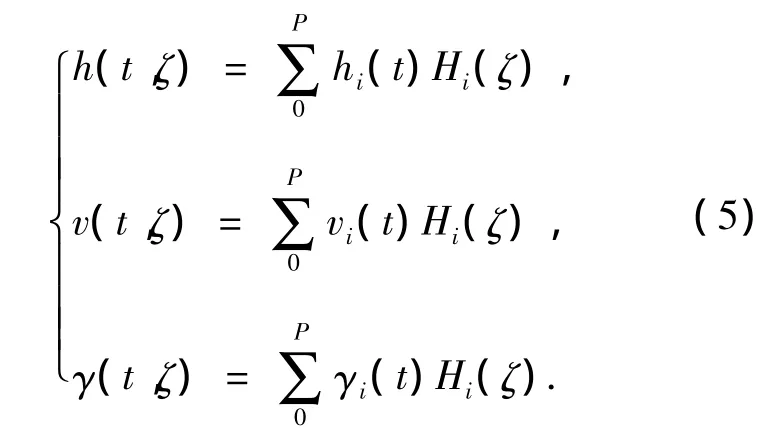
将式(4)～(5)带入到方程(1)～(2)描述的随机微分方程中，可以得到

为了使上式更加简便，做以下假设:

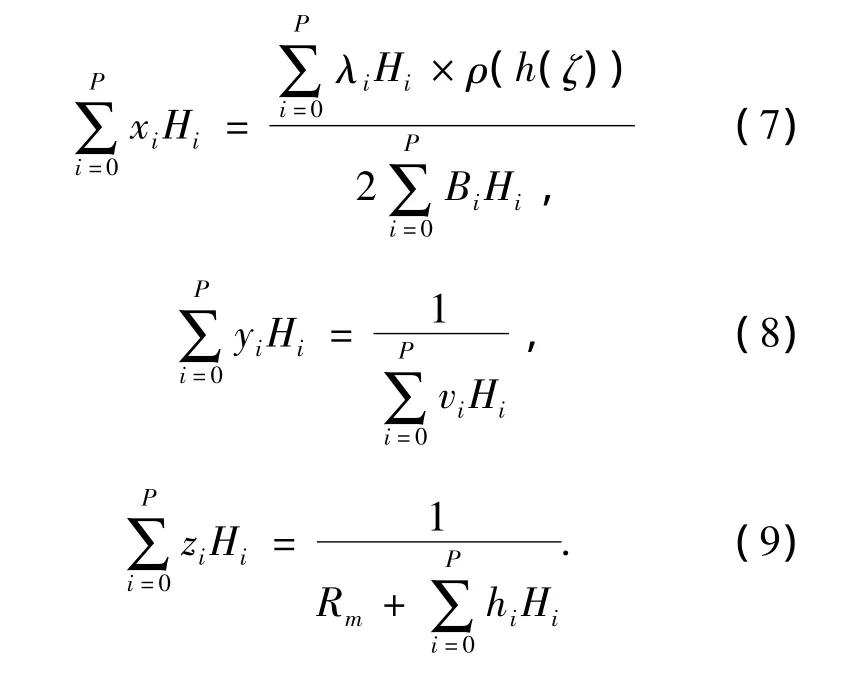
并利用Galerkin投影法则将式(6)投影到正交多项式的基Hm(ζ)上，则可以得到

其中，m=0，1，…，P.方程(10)为与随机微分方程(1)等价的高维确定性微分方程，可以通过龙哥－库塔等算法对此微分方程进行求解，并通过方程(5)可以得到系统状态的统计特性.

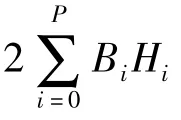
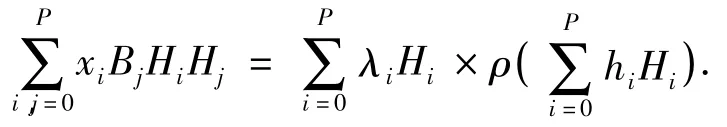
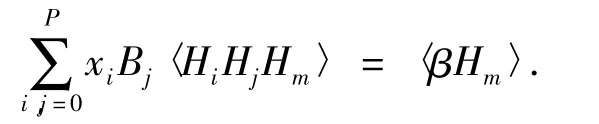
由此，xi可以通过以下方程组求解:

其中M的元素为

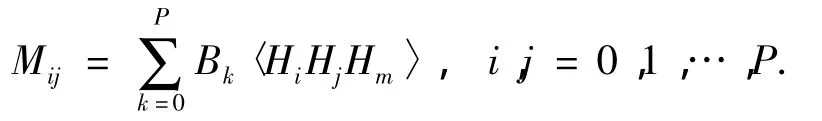
2.3 状态统计特性的求取

在利用式(10)求得混沌多项式的系数之后，着陆器的各状态量可以用式(5)表示，然后根据定义，可求得各个状态量的均值和方差，由于结构类似，本文仅给出高度的均值和方差计算公式，其它状态量的方差和均值可以类比得到，高度的均值为

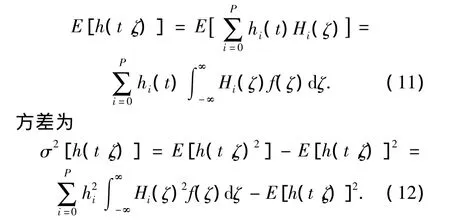
另外，需要指出两点:1)本文方法不仅能得到随机变量的方差和均值，而且可以根据定义通过式(5)求得随机变量的任意阶矩;2)本文仅针对不确定性输入符合高斯分布的情况进行了分析，如果不确定性输入服从其他标准分布，可以根据表1选择对应的正交多项式来代替上述公式中的Hermite多项式，最后所得统计特性计算公式形式与式(10)～(12)完全一样.

3 数学仿真与分析

为验证所提算法的可行性，同时分析各种不确定性因素对落点偏差的影响，本文针对不同的初始误差，分别利用蒙特卡洛仿真方法和本文方法进行数学仿真，着陆器气动参数与标称轨迹初始条件如表2所示.

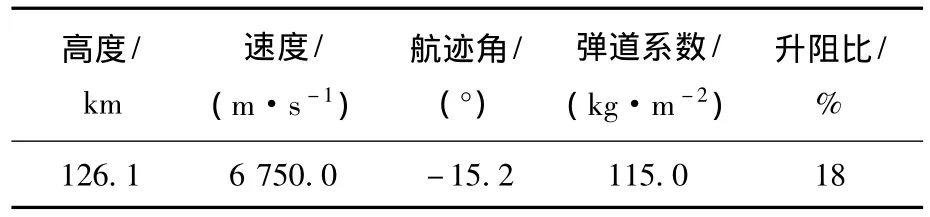
表2 着陆器相关参数与标称轨迹初始条件

假设系统中的弹道系数、升阻比以及大气密度建模均存在10%的不确定性，而初始状态高度存在5 km的不确定性，初始速度存在5 m/s的不确定性，初始航迹角存在0.03°的不确定性，同样假设符合高斯分布.

仿真采用二阶Hermite多项式，蒙特卡洛仿真进行10 000次，仿真计算机CPU为Q8400，主频2.66 GHz，内存3.49 G，仿真软件用Mathworks公司的Matlab2009a.

从图1～图6可以看出，在各种仿真条件下，本文基于混沌多项式展开的方法(PCE)与蒙特卡洛仿真方法(MC)所得到的结果都能够很好吻合，为了更清楚地评价本文方法结果的精确程度，定义相对误差:

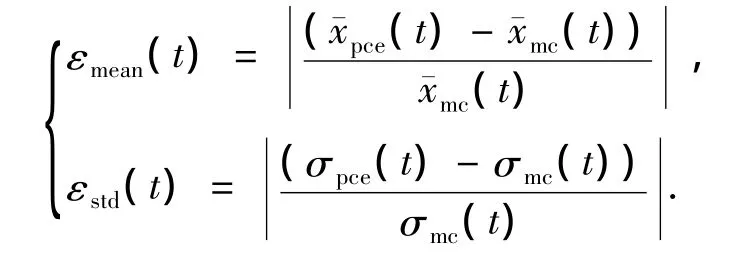
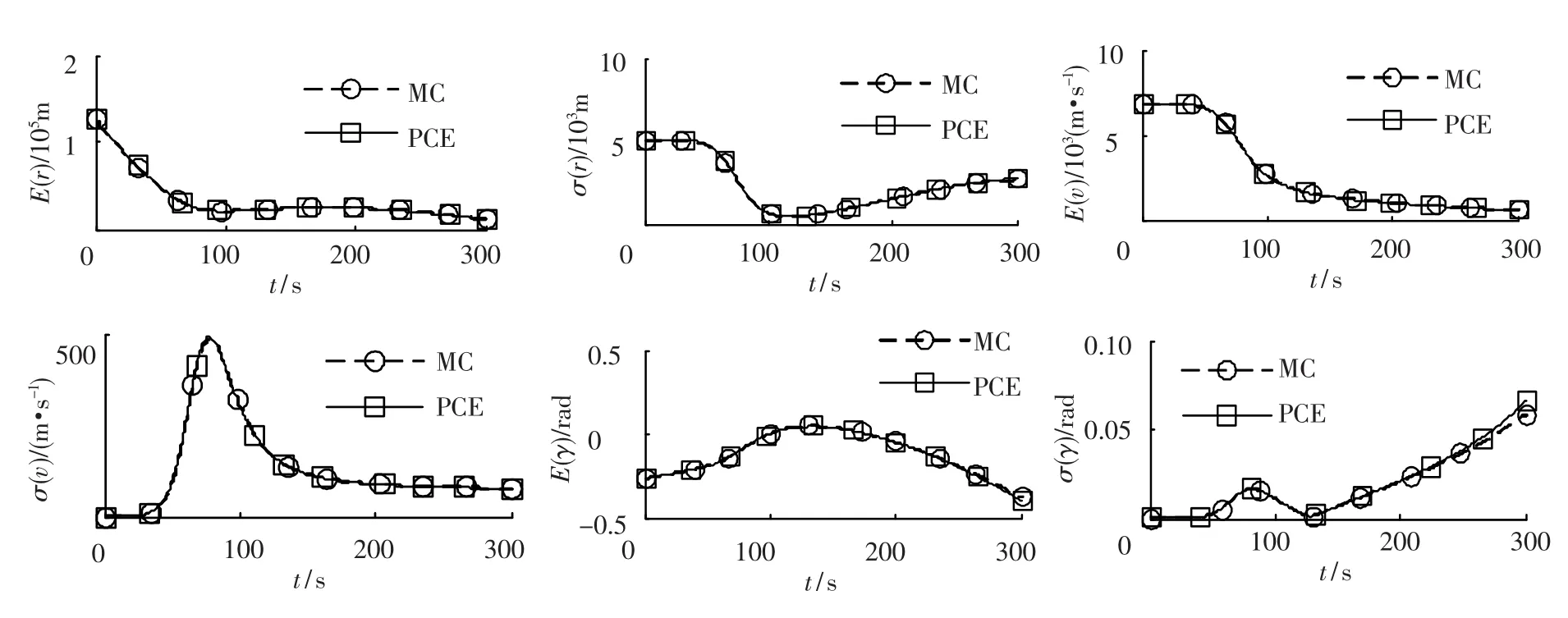
图1 考虑高度不确定性

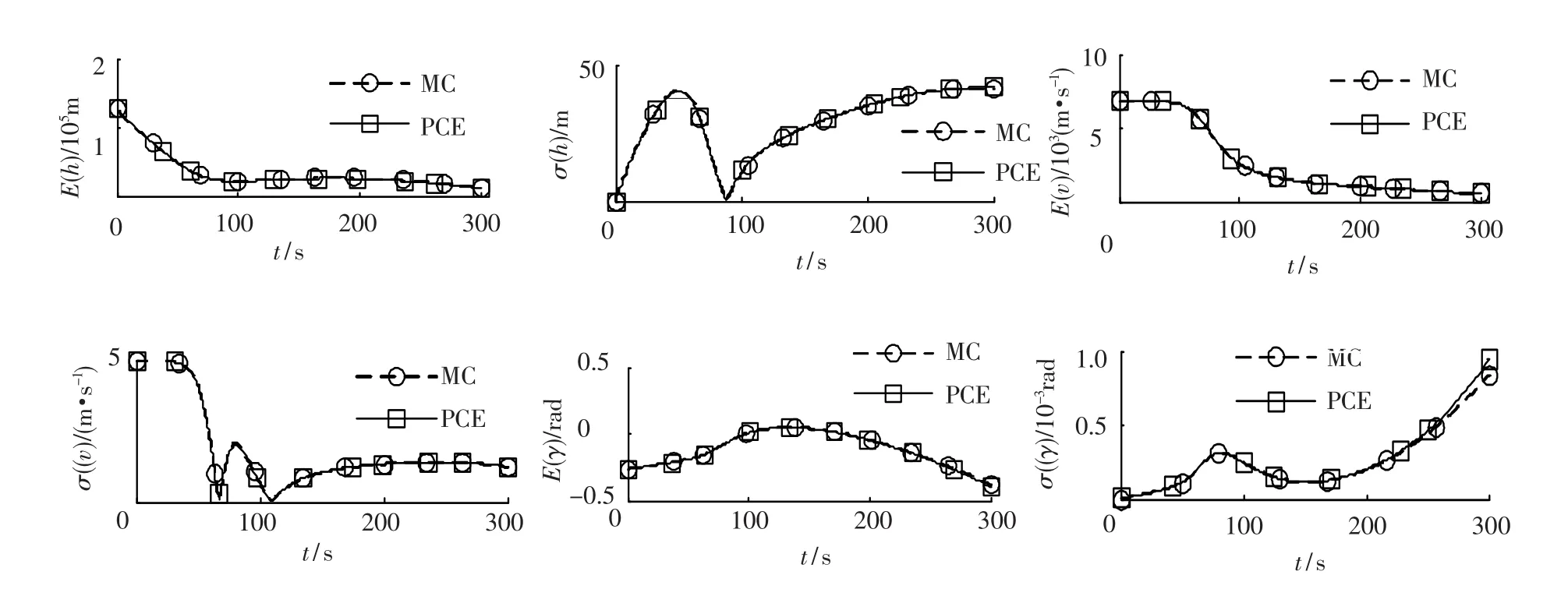
图2 考虑速度不确定性

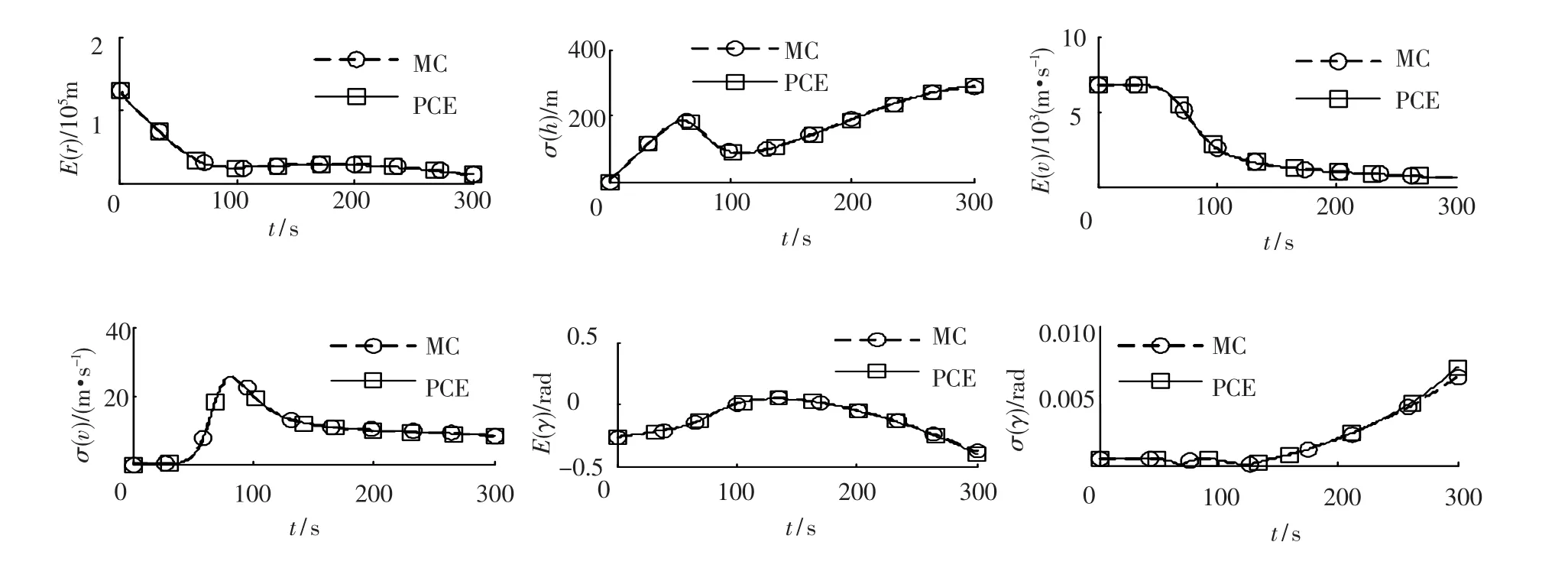
图3 考虑航迹角不确定性

图4 考虑大气密度不确定性

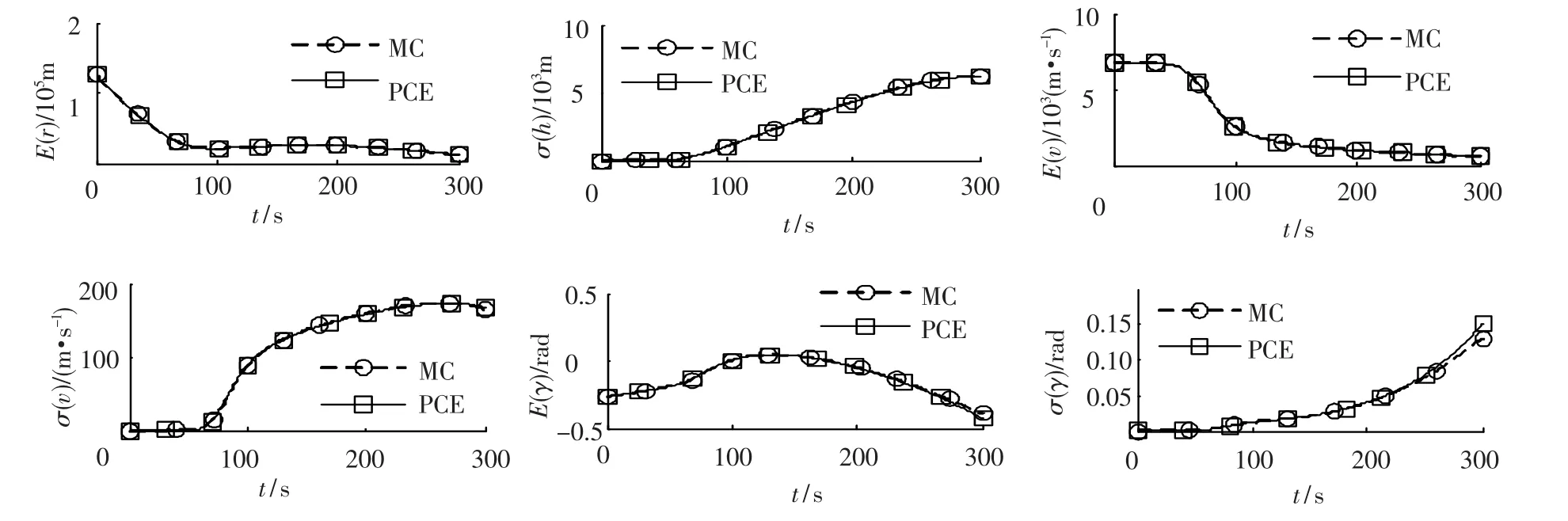
图5 考虑升阻比不确定性

图6 考虑弹道系数不确定性

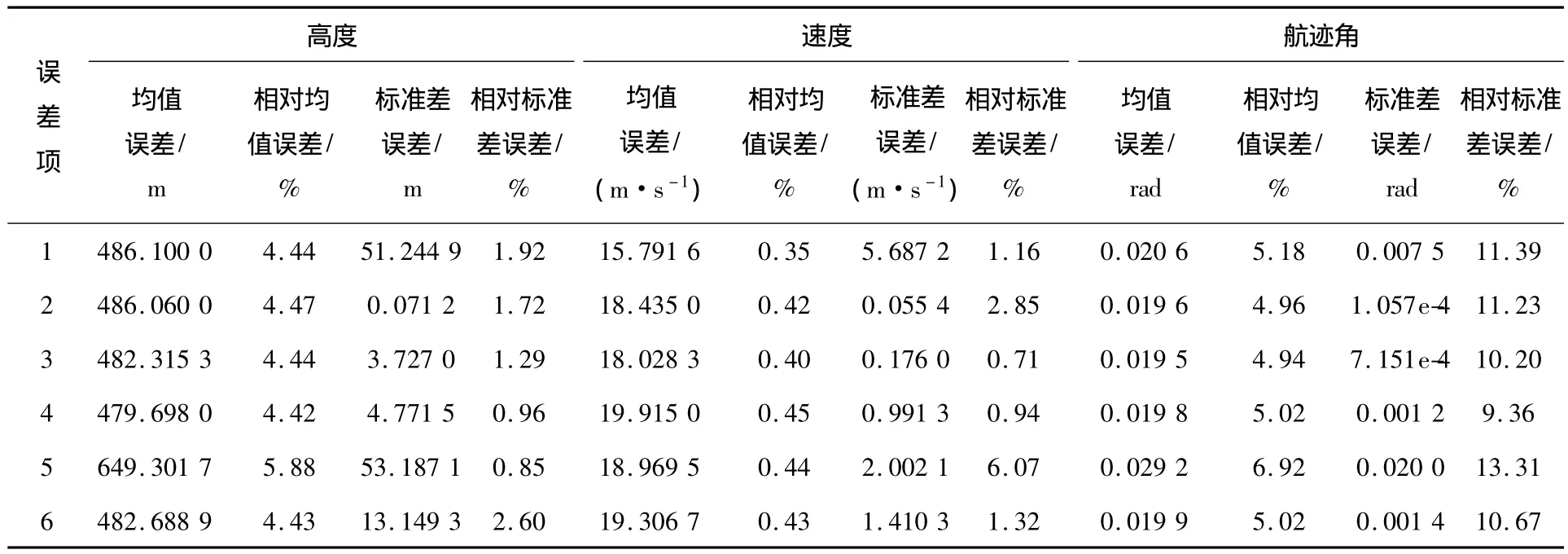
表3 均值－标准差估计误差及相对误差

从表3可以看出，所有状态的均值估计相对误差均小于7%，标准差估计误差小于12%，但蒙特卡洛仿真所消耗的时间为2 360.7 s，本文算法消耗的时间为15.09 s，计算效率明显提高.另外，从图4和图6可以看出，仅考虑10%的大气密度不确定性和仅考虑10%的弹道系数不确定性时，系统状态量统计特性变化趋势一致，原因分析如下:

根据式(1)可知，大气密度不确定因子和弹道系数在动力学方程中总是同时出现，只是所处的位置不同.仅考虑大气密度不确定性时，相当于在对应项处乘以随机变量1+0.1ζ，仅考虑弹道系数不确定性时，相当于在对应项处除以随机变量1+0.1ζ，其中ζ是符合标准正态分布的随机变量，对于小量0.1ζ有

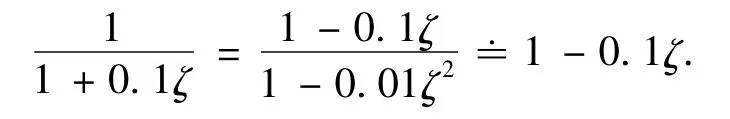
又因为对于零均值的标准正态分布ζ来说，1+0.1ζ和1-0.1ζ符合相同的分布，所以仅考虑大气密度不确定性和仅考虑弹道系数不确定性两种情况结果类似.

4 结论

本文针对火星着陆落点误差评估这一问题做了相关研究，主要工作和研究结论如下:

1)提出了一种基于Galerkin投影的火星着陆落点误差分析方法，该方法以Askey正交多项式和Galerkin投影法则为理论基础，将描述着陆器动力学方程的随机微分方程转换成为1个等效的高维确定性微分方程，通过求解此确定性微分方程，实现对着陆器状态不确定性进行快速分析.

2)以系统不确定性符合高斯分布为例，分别针对6种情况对算法的有效性进行了仿真验证，通过和蒙特卡罗仿真结果对比可以看到:利用2阶Hermite多项式对系统状态进行逼近，则本文算法对状态的均值估计误差小于7%，标准差估计误差小于12%，并且计算效率大为提高;

3)通过仿真发现大气密度不确定性和弹道系数不确定性所引起的着陆器状态统计特性变化趋势大体一致，并对产生这种现象的机理在理论上进行分析;

4)这种算法可以推广到系统不确定性为非高斯白噪声的情况，只需相应的调整概率密度函数，选择合适的正交多项式代替仿真中的Hermite多项式，算法流程及推导的等效高维确定性微分方程形式不变.

［1］BRAUN R D，MANNING R M.Mars exploration entry，descent，and landing challenges［J］.Journal of Spacecraft and Rockets，2007，44(2):310 －313.

［2］WOLF A，GRAVES C，POWELL R，et al.Systems for pinpoint landing at Mars［C］//14th AIAA/AAS Space Flight Mechanics Meeting.Pasadena:Jet Propulsion Laboratory，National Aeronautics and Space Administration，2004:1－20.

［3］SHEN Hai-jun，SEYWALD H，POWELL R.Desensitizing the pin-point landing trajectory on Mars［C］//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Pasadena:Jet Propulsion Laboratory，National Aeronautics and Space Administration，2008:1130－1143.

［4］FISHMAN G S.Monte carlo:concepts，algorithms and applications［M］.New York:Springer-Verlag，1996:66 －70.

［5］FOX B.Strategies for quasi-monte carlo［M］.Boston:Kluwer Academic Publishers，1999:305 －323.

［6］GAMERMAN D，LOPES H.Markov chain monte carlo:stochastic simulation for bayesian inference［M］.New York:Chapman＆ Hall/CRC，2006:121－136.

［7］BROWN R G，HWANG P Y C，Introduction to random signals and applied Kalman filtering:with MATLAB exercises and solutions［M］.Wiley:Chichester，1992:335 －377.

［8］WAN，E，VAN DER MERWE R.The unscented Kalman filter for nonlinear estimation［C］//Adaptive Systems for Signal Processing，Communications，and Control Symposium.Piscataway:IEEE Inc，2000:153－158.

［9］XIU Dong-bin，KARNIADAKIS G E.Modeling uncertainty in flow simulations via generalized polynomial chaos［J］.Journal of Computational Physics，2003，187(1):137－167.

［10］SPANOS P，GHANEM R.Stochastic finite element expansion for random media［J］.Journal of Engineering Mechanics，1988，115(5):1035 －1053.

［11］GHANEM R.Ingredients for a general purpose stochastic finite elements implementation［J］.Computer Methods in Applied Mechanics and Engineering，1999，168(1):19－34.

［12］PRABHAKAR A，FISHER J，BHATTACHARYA R.Polynomial chaos-based analysis of probabilistic uncertainty in hypersonic flight dynamics［J］.Journal of Guidance，Control，and Dynamics，2010，33(1):222 －234.

［13］WIENER N.The homogeneous chaos［J］.American Journal of Mathematics，1938，60(4):897－936.

［14］XIU Dong-bin，KARNIADAKIS G E.The wiener-askey polynomial chaos for stochastic differential equations［J］.SIAM Journal on Scientific Computing，2002，24(2):619－644.

A new landing site uncertainty analysis method for mars entry mission

REN Gao-feng1，ZHU Sheng-ying2

(1.School of Astronautics，Harbin Institute of Technology，150080 Harbin ，China;2.School of Aerospace Engineering，Beijing Institute of Technology，100081 Beijing，China)

To evaluate how the uncertain factors in the entry dynamics such as the navigation errors at the entry point affect the landing precision effectively，by introducing the Galerkin projection，a rapid landing error prediction method for Mars entry is proposed.In this method，the Polynomial Chaos are used to approximate the vehicle＇s states，and the problem is converted to a deterministic dynamical systems.Applying the method to a representative entry scenario of our country＇s future Mars entry mission，simulation results indicate that，compared with Monte Carlo method，the proposed method is able to predict the mean and covariance with little error and more computational efficiency.

landing error;orthogonal polynomial;mars landing;galerkin projection

V448.15

A

0367－6234(2012)07－0014－07

2011－06－23.

国家高技术研究发展计划重点资助项目(2010122206).

任高峰(1983—)，男，博士研究生.

任高峰，stone－breaker@126.com.

(编辑 张 宏)