空间机器人终端滑模路径跟踪控制

胡庆雷，徐 梁，霍 星，马广富

(哈尔滨工业大学控制科学与工程系，150001 哈尔滨)

空间机器人终端滑模路径跟踪控制

胡庆雷，徐 梁，霍 星，马广富

(哈尔滨工业大学控制科学与工程系，150001 哈尔滨)

对存在摩擦干扰力矩的自由漂浮空间机械臂任务空间路径跟踪控制问题采用终端滑模，实现了跟踪误差的有限时间镇定.同时考虑执行机构存在的死区特性，设计了自适应补偿机构，通过自适应控制来学习死区特性的上界，以确保跟踪控制的有效执行.最后基于Lyapunov方法，从理论上证明了闭环系统的全局稳定性，并通过数值仿真证明此控制器能够有效实现任务空间路径跟踪控制，且对干扰具有一定的鲁棒性.

自由漂浮空间机械臂;路径跟踪;终端滑模;死区特性;自适应

在未来的空间活动中，众多技术人员［1－3］认识到利用机器人协助完成诸如交会对接、空间站在轨组装以及航天器的日常维护工作等是一种最佳选择.空间机器人执行任务时，都需要对机械臂末端执行器在任务空间内进行路径跟踪控制.当本体姿态不受控时，由于存在角动量守恒，自由漂浮空间机器人是1个典型的欠驱动二阶非完整系统，其任务空间路径跟踪控制问题比地面机器人更为复杂.

对于空间机器人，如何设计任务空间路径跟踪控制器，目前己有一定的研究成果.文献［4］在空间机器人本体姿态受控的情况下，考虑环境干扰的存在，设计了终端滑模跟踪控制器，实现末端执行器的任务空间快速跟踪控制.文献［5］同样针对本体姿态受控的空间机器人系统，设计了末端路径跟踪控制器.考虑到更为广泛的自由漂浮状态，在空间机器人系统本体姿态不受控时，文献［6－7］设计了任务空间路径跟踪控制器，但控制器形式复杂，需求解配平项，实现起来十分困难.而且上述文献都没有考虑工程中执行机构本身的非线性特性，从而大大限制了其实际应用.

为此，本文在上述研究结果的基础上，针对本体姿态不受控的空间机器人任务空间路径跟踪问题，提出一种自适应终端滑模控制器，以实现摩擦干扰力矩和执行机构死区特性存在时，系统任务空间的快速有效跟踪.该方法采用自适应控制技术在线学习、估计系统中不确定参数，同时变结构控制器的采用也使得系统对外界的干扰具有一定的鲁棒性.Lyapunov稳定性分析证明该跟踪控制器能够实现对末端抓手的全局渐近跟踪控制.最后，将该控制方法应用于平面两连杆自由漂浮空间机器人，仿真结果表明，此方法能够在干扰因素存在时，实现末端抓手的任务空间路径跟踪控制.

1 模型建立

不失一般性，考虑作平面运动的两关节自由漂浮机械臂，系统结构如图1所示.整个系统由本体 B0、Bi(i=1，2)连杆组成.

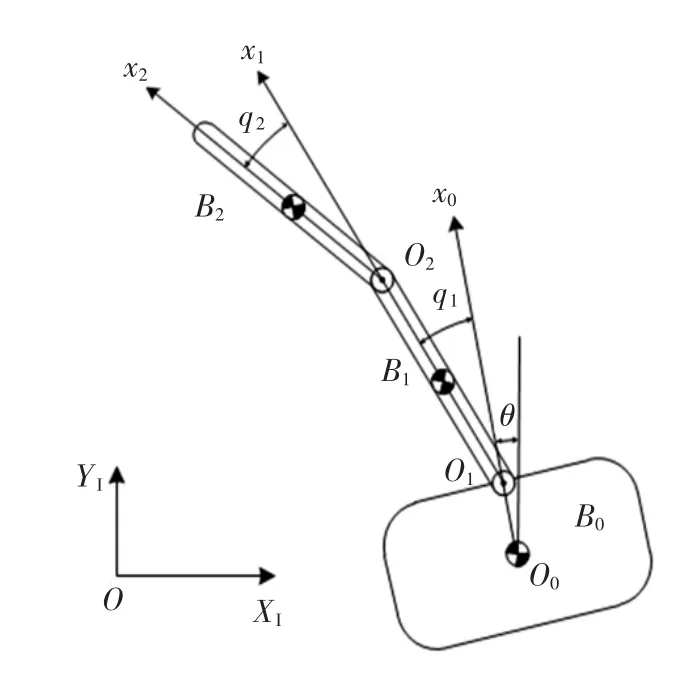
图1 平面两连杆自由漂浮机械臂系统

其符号定义如下:b0为本体质心O0到关节O1的距离;li为连杆 Bi(i=1，2)的长度;mi为Bi(i=0，1，2)的质量;Ji为Bi(i=0，1，2)的相对于质心的转动惯量;OXIYI为惯性空间坐标系标架;θ为x0与YI轴的夹角;qi为xi-1轴与xi轴之间的夹角(i=1，2);rp为末端执行器的位置向量.

假设此刚性空间机械臂本体的位置和姿态都不受控，则在运动过程中，系统满足线动量和角动量守恒，相应的，动力学方程可以表示为下列形式:

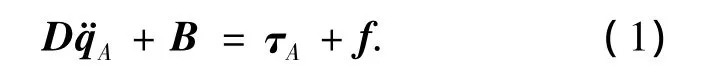
其中qA=［θ q1q2］T;D∈R3×3为系统的惯量矩阵;B∈ R3×1包含向心力和科氏力项;τA=［0 τ］T∈ R3×1表示系统的广义输入，τ =［τ1τ2］T分别是两个关节的执行机构输出力矩;fA=［0 f］T∈R3×1表示系统的广义摩擦力矩，f=［f1f2］T分别表示作用于两个关节上的摩擦力矩.

如果定义X=［xeye］T表示机械臂末端执行器在惯性空间中的位置矢量，由系统的几何关系以及动量守恒，可得到如下的运动学方程:

其中 q= ［q1q2］T，J ∈ R2×2表示广义雅可比矩阵.

由于机械设计和制造方面的原因，系统执行机构通常都会存在“死区”特性，会恶化系统的调节品质，影响系统的输出精度.执行机构的死区特性对控制系统造成的影响可以用图2来表示，其中u代表控制输入，τ代表执行机构输出，通常情况下，两者并不相同.

图2 执行机构死区特性

一般情况下，系统执行机构的死区特性可用控制输入u与执行机构输出τ之间的关系来描述，为简化起见，本文考虑如下死区特性:

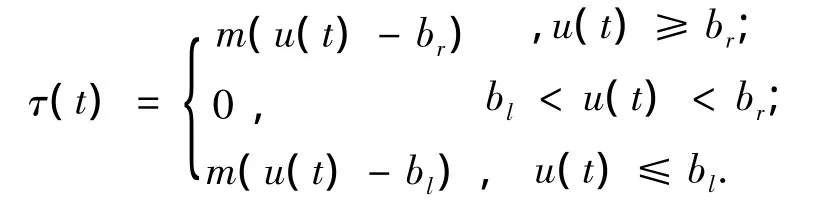
其中br＞0、bl＜0、m ＞0均为常值;u代表控制输入;τ代表执行机构的输出，据此可以将执行机构的输出分为两部分，即

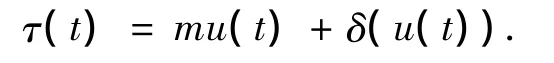
其中:

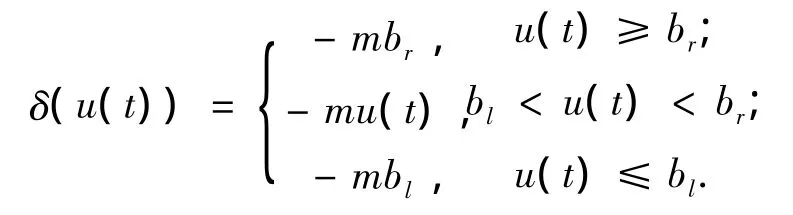
描述了执行机构的死区特性，而mu(t)则代表执行机构的对控制输入的响应.

针对自由漂浮空间机器人系统(1)～(2)，在全局范围内作如下假设.

假设1 关节摩擦力矩f有界，且满足

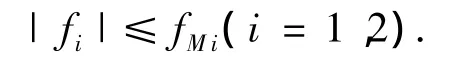
其中fMi(i=1，2)为未知的正常数，是向量fM∈R2×1的元素.

假设2 执行机构的死区特性δ是有界的，即

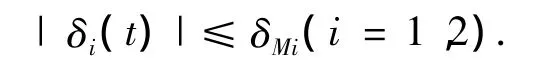
其中δMi(i=1，2)为未知的正常数，是向量δM∈R2×1的元素.

假设3 系统在跟踪指定参考路径Xd时，运动过程中不存在奇异位形，即|J|≠0.

注1 通常情况下，空间机械臂的雅可比矩阵J会出现运动学和动力学奇异现象，导致逆运动学无法求解，但在实际路径跟踪时，会首先进行路径规划，选取一条不发生奇异的路径，因此假设3是合理的.

至此，本文的控制目标是针对系统(1)～(2)，当存在执行机构死区特性以及摩擦干扰力矩时，在假设1、2、3的条件下，设计控制律τ，使得系统输出X跟踪指定的参考路径Xd.

2 模型变换

从系统的动力学方程(1)可以看出，自由漂浮空间机器人系统是1个欠驱动机械系统，可以证明在本体姿态不受控制时，系统存在二阶非完整约束，为实现空间机器人系统的路径跟踪，需对模型进行一定的变换.

对式(1)展开可以得到

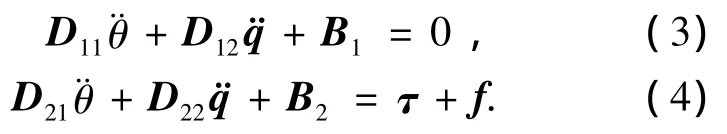
由矩阵D可逆［10］，可知D11可逆，于是从式(3)中可得

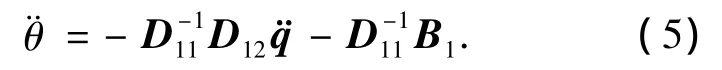
结合式(4)，刚性自由漂浮空间机器人的动力学方程可以改写为如下形式:

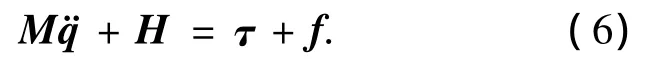
其中

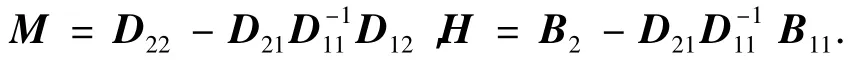
注2 由矩阵D正定对称可知，矩阵M正定对称.这样得到了关节控制力矩与关节转角的动力学方程，从方程的形式中可以看出，这是1个全驱动的二阶系统，控制输入为空间机械臂的关节力矩，输出量为关节转角.

为实现任务空间的轨迹跟踪任务，必须得到控制力矩与机械臂末端执行器位置之间的动力学方程.对运动学方程(2)两边进行微分可以得到

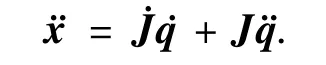
可知，关节转角的加速度与末端执行器运动加速度和速度之间的关系如下:

将上式代入式(6)中，经过化简可得

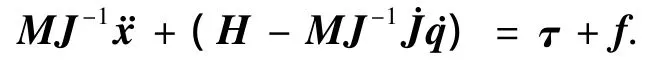
定义

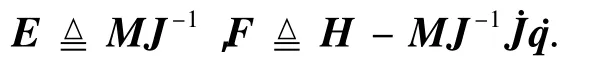
这样可以得到从输入关节控制力矩τ到末端执行器位置矢量X的动力学方程为

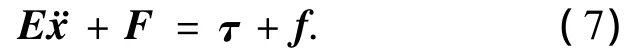
注3 由矩阵M、J可逆，可知矩阵E可逆.此时，对自由漂浮空间机器人系统(1)～(2)的任务空间路径跟踪简化为对系统(7)的跟踪控制问题，下面将针对存在摩擦干扰力矩和输出死区特性的情况下，设计控制器，使得X可以跟踪指定的参考路径Xd.

3 滑模自适应控制器设计

滑模变结构控制对非线性系统参数摄动、外界扰动具有很好的鲁棒性，在机器人、飞行器等众多领域广泛应用.终端滑模(TSM)［11］控制器因具有使系统状态在有限时间内收敛到平衡点的优点，相对于传统的线性滑模控制器具有更高的稳态跟踪精度，因此本文采用终端滑模来实现系统的有限时间跟踪，并在控制器的设计中，考虑摩擦干扰力矩与系统执行机构的死区特性，使控制器具有一定的工程应用价值.

假设Xd=［xedyed］T是末端执行器在任务空间中期望的跟踪路径，这样可以得到系统的跟踪误差向量为e=X-Xd.

则由式(7)可知，跟踪误差与控制输入之间有如下的关系:

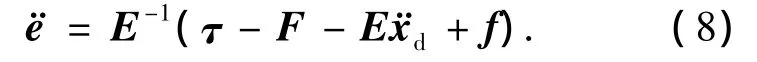
注4 对向量 z∈ Rn×1，定义

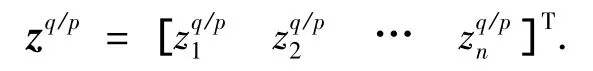
设计滑动模态面如下［11］:

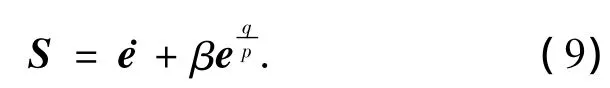
其中β为正常数，q、p为正奇整数，且满足条件q＜p.可知，当系统到达滑动模态面S=0之后，误差将在有限时间 tf内收敛到零［11］，tf表达式如下:

其中e(0)表示系统到达滑模面时的初始误差向量.

注5 Λ(·)表示以向量·为对角线元素的对角矩阵.

对滑模面S进行时间的一阶微分可得到

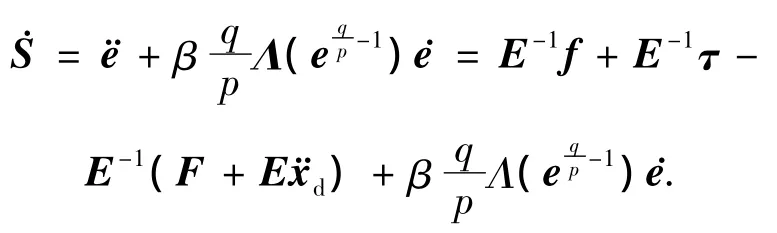
定义如下向量:

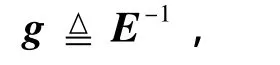
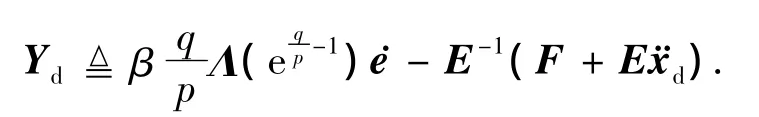
可以得到的关于系统滑动模态面的动力学方程为

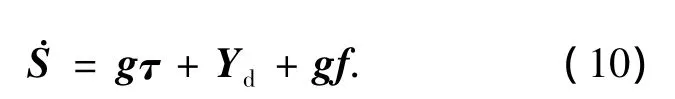
其中Yd代表系统中的已知量.于是，对系统(1)～(2)的路径跟踪问题转化为对系统(10)的镇定控制问题，如果能够使系统在有限时间内到达滑动模态面，那么末端执行器将在有限时间内到达并沿着指定路径运动.

当考虑执行机构死区特性时，可以将式(10)写成如下的形式:

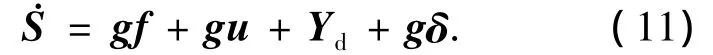
其中gδ代表了执行机构的非线性死区特性对控制系统所造成的影响，δ为系统的死区特性的描述，是一个与控制输入u无关的非线性项.

为弥补死区特性以及摩擦干扰力矩对控制系统所造成的影响，本文在变结构控制的基础上，设计了自适应补偿机构，整个系统的结构如图3所示.

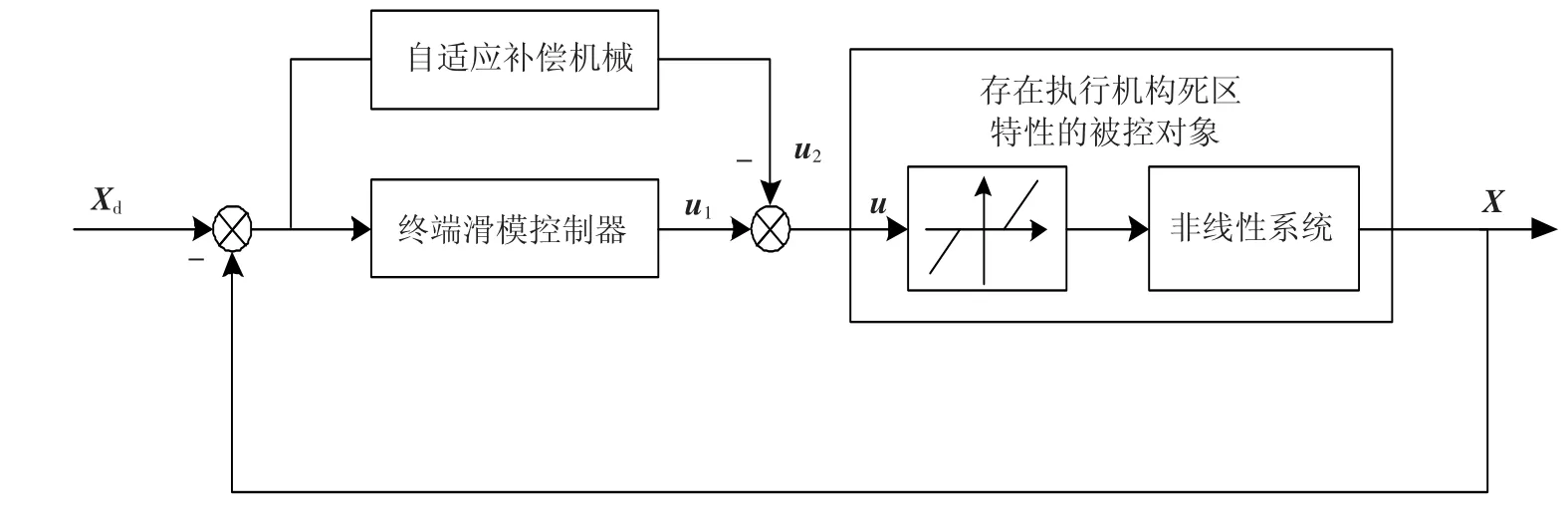
图3 带有补偿机构的控制系统

控制输入包含两部分:

其中:

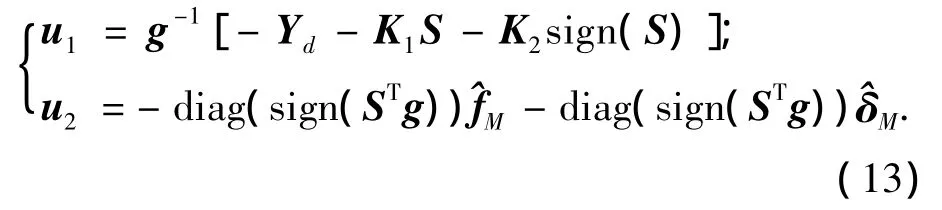
其中K1、K2为正定的对角矩阵;^fM、^δM为对系统摩擦干扰力矩和执行机构死区特性上界的估计值.

上述控制律中u1代表系统的滑模变结构控制器的输出控制指令，其设计目的是使系统的跟踪误差在有限时间内到达滑动模态面，进而实现系统跟踪误差的有限时间镇定.u2代表控制自适应补偿机构的输出，它被设计用来消除系统执行机构的死区特性以及摩擦干扰力矩对系统跟踪所造成的影响.其参数的更新律设计如下:

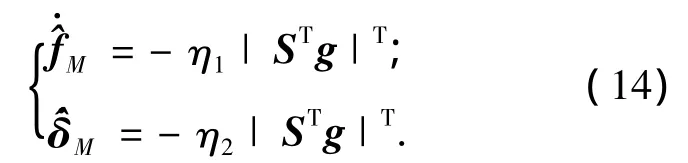
注6 对向量 s∈ Rn×1，定义

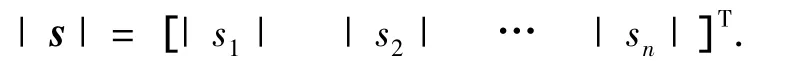
其中|si|(i=1，2，…，n)代表标量si的绝对值.

定理 针对系统(1)～(2)，在存在摩擦干扰力矩和执行机构死区特性的情况下，若满足假设1、2、3，采用控制律(12)～(13)和自适应更新律(14)，系统跟踪误差将在有限时间内收敛到零.

证明 考虑如下的Lyapunov函数:

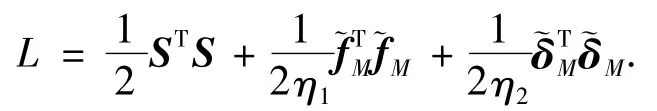
对上述Lyapunov函数求取对时间的一阶微分可得

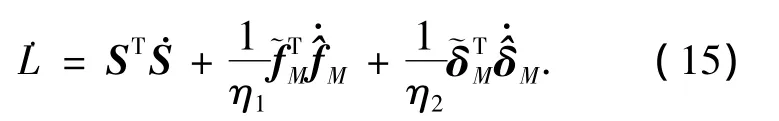
将式(11)～(12)代入式(15)中可得

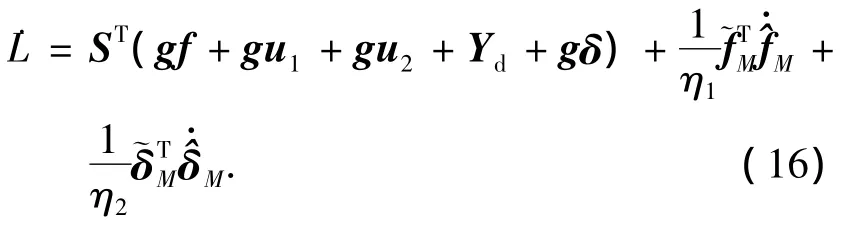
将控制输入(13)代入式(16)，经过化简可以得到

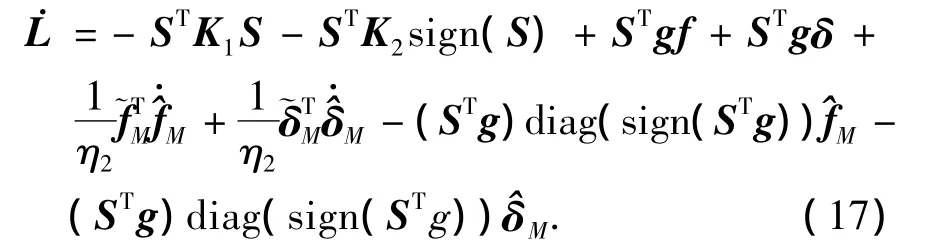
由前文定义可知

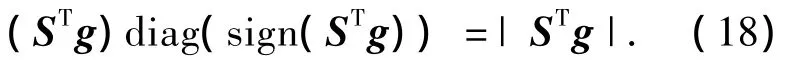
注意到

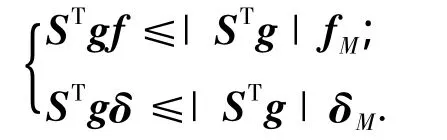
因此

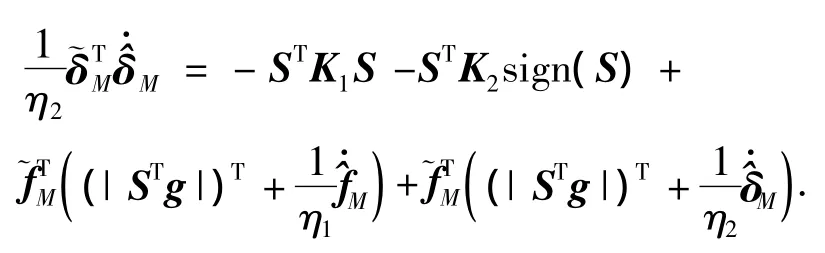
代入自适应更新律(14)可得

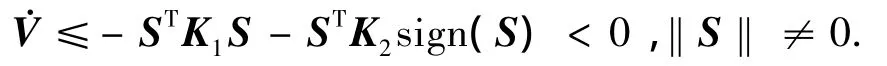
由此可知，系统将在有限时间内到达滑动模态面S，由终端滑模特性可知，在此之后，经过有限时间tf，系统的跟踪误差将达到零，也就意味着系统的跟踪误差将在有限时间内收敛到零.至此，定理得证.

注7 控制律(13)的Yd中含有负指数项，对于表示滑动模态面的式(9)，如图4所示.

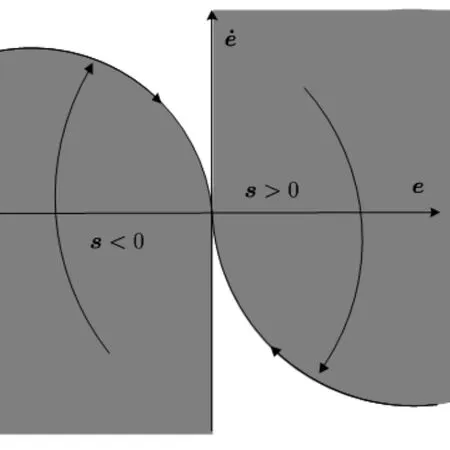
图4 系统相轨线

如果e先于s收敛到零，也即系统轨线穿越e=0轴，则会出现奇异现象，会导致所得到的Yd有限时间内无界，进而导致控制u1在有限时间内无界.因此系统初始值的选取必须满足图中所示的阴影区域，即

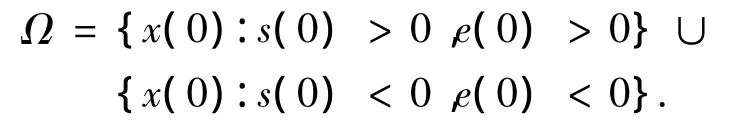
4 仿真验证

为验证本文所提出控制器的有效性，将其应用于图1所示的系统进行仿真.实际机械臂系统物理参数选取如表1.

表1 空间机器人仿真参数

此外，为满足不发生奇异条件，机械臂的初始状态选取如下:

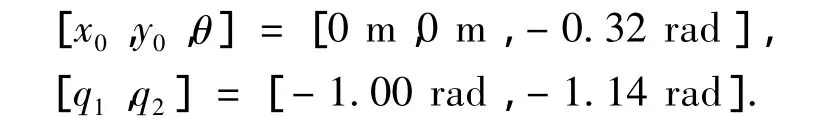
期望的末端执行器跟踪路径为

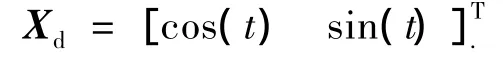
摩擦干扰力矩选取为

其单位为N·m.

假设执行结构的非线性特性参数为

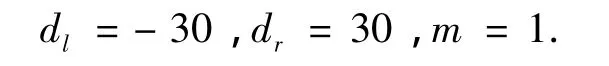
控制器增益选取如下:

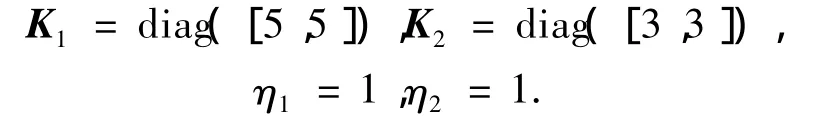
为进行对比，本文采用反馈线性化［12］进行对比，考虑如下4种情况进行仿真比较.

第一种情况.假设不存在摩擦干扰力矩和执行机构死区特性，分别采用这两种方法，跟踪参考路径.

第二种情况.假设只存在执行机构死区特性，分别采用3种方法，跟踪参考路径.

第三种情况.假设摩擦干扰力矩及执行机构死区特性同时存在，采用本文提出的方法，跟踪参考路径.

第四种情况.假设不存在摩擦干扰力矩和执行机构死区特性，对本体姿态施加干扰力矩，采用本文提出的方法，进行末端路径跟踪控制.

其中文献［11］反馈线性化控制器在仿真中采用形式如下:

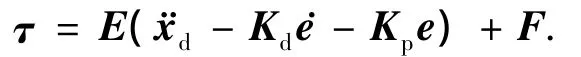
其控制器参数选取为

第一种情况.假设不存在摩擦力矩和执行机构死区特性，其仿真结果如图5所示.从仿真结果可以看出，在跟踪指定的参考路径时，当不考虑摩擦力矩和执行机构死区特性时，采用本文所提出的自适应终端滑模控制，系统的响应速度非常快，理论上采用终端滑模控制，系统的跟踪误差将在有限时间内收敛到零，而采用反馈线性化的控制结果，跟踪误差只有在时间趋向于无穷远时才会收敛到零.同时，终端滑模的控制方法，可以通过调节参数控制收敛速度，使其具有更高的跟踪性能.

第二种情况.假设只存在执行机构死区特性，其仿真结果如图6所示.由仿真结果可以看出，在这种情况下，采用反馈线性化的控制方案，系统是发散的，甚至还出现了奇异现象，而没有开启自适应补偿机构的滑模控制器同样也出现了跟踪误差较大的情况，说明研究执行机构的死区特性是十分有必要的.

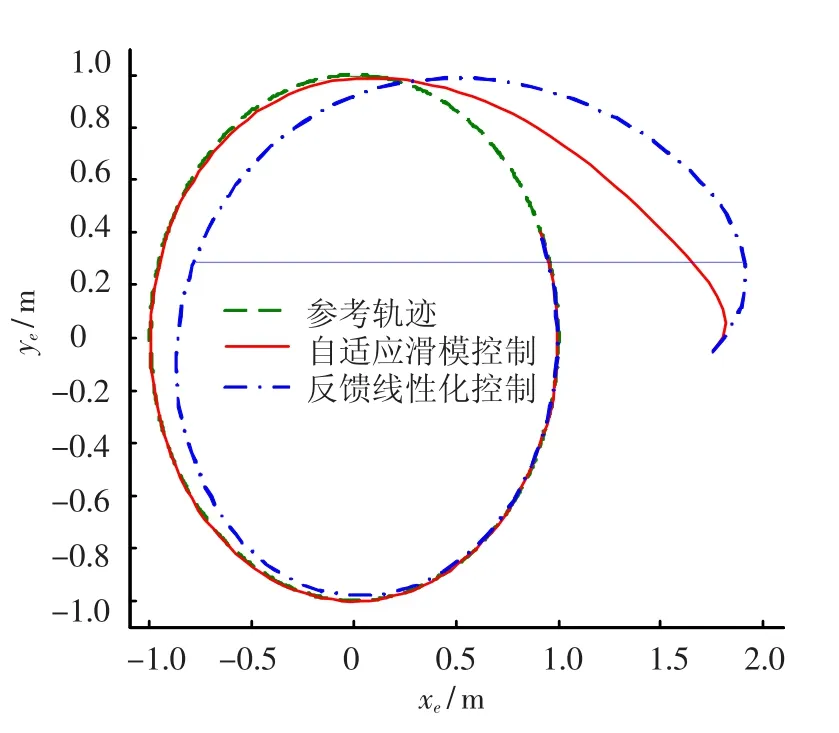
图5 理想情况下仿真结果

图6 存在执行机构死区特性时的仿真结果

当对终端滑模控制器采用自适应补偿机构后，在执行机构存在死区特性时，仿真结果如图7所示，可以看出系统的跟踪性能有较大的改善，而且同图6对比可以发现，自适应补偿机构较好的弥补了执行机构死区特性所造成影响，表明设计有效.

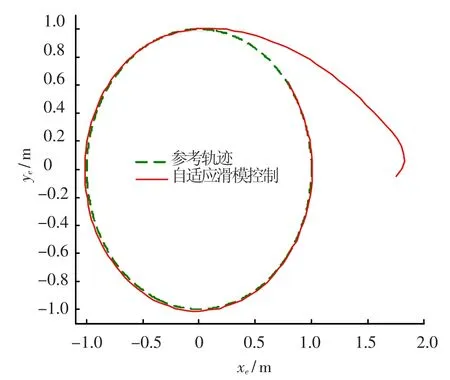
图7 带有补偿机构的滑模控制仿真结果

第三种情况.假设摩擦力矩和执行机构死区特性同时存在，其仿真结果如图8所示.从图中可以看出，系统的跟踪效果很好，很快跟踪上指定路径，且对干扰具有一定的鲁棒性.

第四种情况.假设还存在对本体姿态的扰动.通常情况下，环境干扰力矩对基座姿态还会造成相当大的影响，这都会对空间机械臂系统执行末端路径跟踪造成一定的影响，为了研究，在本文中假设系统本体存在周期性的脉冲干扰力矩.假设此干扰力矩周期为2 s，幅值为100 N·m，脉冲宽度为0.02，同时仍假设摩擦干扰力矩和执行机构死区特性存在，采用本文所提出的自适应终端滑模进行控制仿真，结果如下图9所示.从图9中可以看出，系统在本体姿态存在扰动时，末端仍能有效跟踪指定路径.

通过如上对比，可以看出当存在摩擦干扰力矩和执行机构死区特性，甚至存在对本体姿态扰动时，本文所提出的控制器仍能有效完成跟踪任务，表明了控制器设计的有效性.

图8 摩擦及死区特性存在时系统跟踪输出

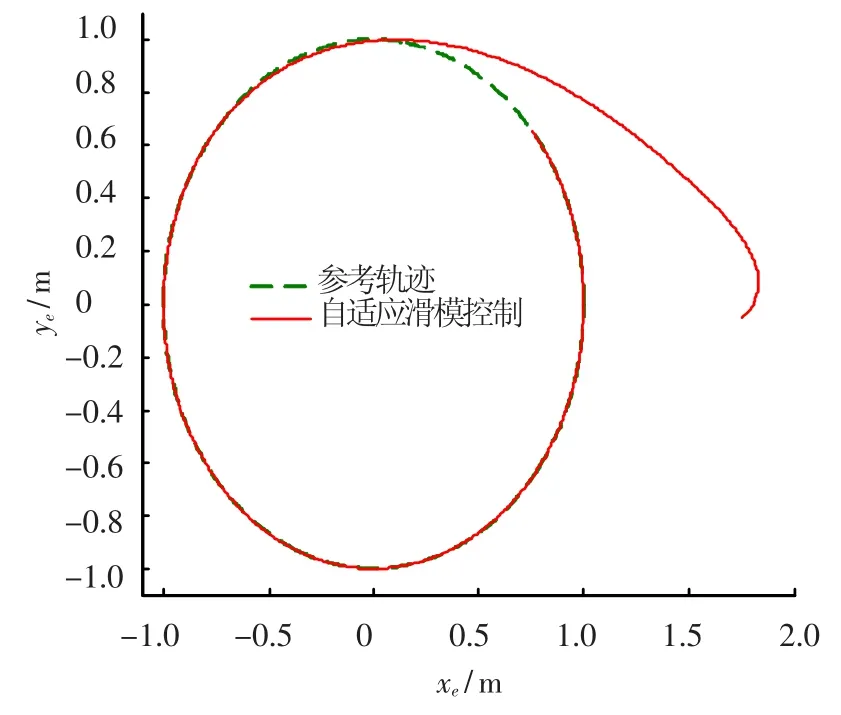
图9 本体存在干扰时的仿真结果

5 结论

本文设计了终端滑模控制器，使得存在摩擦干扰力矩和执行机构死区特性的自由漂浮空间机械臂，能够在有限时间内跟踪上指定的参考路径.由于考虑到了空间机械臂系统执行机构的死区特性，使得该控制器具有一定的实用价值.最后将本文提出的方法应用于平面两连杆自由漂浮机械臂的跟踪控制仿真，结果表明该方法能够很好的实现跟踪目标，且具有良好的鲁棒性.

［1］EVANS L.Canadian space robotics on board the international space station［C］//2005 CCTOMM Symposium on Mechanisms，Machines and Mechatronics.Montreal:Canadian Space Agency，2005:26－27.

［2］MOOSAVIAN S，PAPADOPOULOS E.Free-flying robots in space:an overview of dynamics modeling，planning and control［J］.Robotica，2007，25(5):537 －547.

［3］MONTEMERLO M.25 years of space automation and robotics at NASA:an historical perspective［R］.Proceeding of the 6th International Symposium on Artificial Intelligence and Robotics and Automation in Space.Quebec:Canadian Space Agency，2001.

［4］郭益深，陈力.漂浮基双臂空间机器人协调运动的Terminal滑模控制［J］.工程力学，2009，26(5):221－227.

［5］GUO Y，CHEN L.Terminal sliding mode control for coordinated motion of a space rigid manipulator with external disturbance［J］.Applied Mathematics and Mechanics，2008，29(5):583 －590.

［6］陈力.带滑移铰空间机器人惯性空间轨迹跟踪的鲁棒混合自适应控制［J］.工程力学，2004，21(3):174－179.

［7］郭益深，陈力.漂浮基双臂空间机器人惯性空间轨迹跟踪的拟增广自适应控制［J］.工程力学，2008，25(1).224－228.

［8］UMETANI Y，YOSHIDA K.Resolved motion rate control of space manipulators with generalized Jacobian matrix［J］.IEEE Transactions on Robotics and Automation，1989，5(3):303－314.

［9］PAPADOPOULOS E，DUBOWSKY S.On the nature of control algorithms for free-floating space manipulators［J］.IEEE Transactions on Robotics and Automation，1991，7(6):750－758.

［10］CHEN L.Adaptive control of dual-arm space robot system in inertial space［C］//IEEE International Symposium on Industrial Electronics.Vigo，Spain:［s.n.］，2007:2043－2046.

［11］FENG Y.Non-singular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38(12):2159－2167.

［12］KHALIL H K.Nonlinear systems［M］.New Jersey:Person Education，2000:46－56.

［13］OLFATI-SABER R.Normal forms for underactuated mechanical systems with symmetry［J］.IEEE Transactions on Automatic Control，2002，47(2):305 －308.

［14］OLFATI-SABER R.Cascade normal forms for underactuated mechanical systems［C］//Proceedings of the 39th IEEE Conference on Decision and Control.Sydney:［s.n.］，2000:2162 －2167.

［15］OLFATI-SABER R.Nonlinear control of underactuated mechanical systems with application to robotics and aerospace vehicles［D］.Massachusetts:Massachusetts Institute of Technology，2001:26－33.

Path-following of free-floating space manipulator system using adaptive terminal sliding mode control

HU Qing-lei，XU Liang，HUO Xing，MA Guang-fu

(Dept.of Control Science and Engineering，Harbin Institute of Technology，150001 Harbin，China)

The tracking problem of free-floating space manipulator system in task space with friction disturbance torque is investigated in this paper.A terminal sliding mode controller is proposed to achieve finite time stabilization of the system.Furthermore，taking into account the existence of dead-zone nonlinearity of the actuator，an adaptive compensator is designed to estimate its upper bound and thus ensure the effectiveness of the proposed controller.Lyapunov stability analysis proves that the closed-loop system is globally asymptotic stable.Numerical simulations show that this controller can effectively achieve inertia space tracking task and also be robust to external disturbances.

Free-Floating space manipulator;path-following;terminal sliding mode control:dead-zone nonlinearity;adaptive control

TH133;TP183

A

0367－6234(2012)07－0001－07

2011－05－16.

国家自然科学基金资助项目(61004072);高等学校博士学科点专项科研基金资助项目(20102302110031);黑龙江省留学回国人员科学基金资助项目(LC08C01);哈尔滨市留学回国基金资助项目(2010RFLXG001);中央高效基本科研业务费专项基金资助项目(HIT.NSRIF.2009003).

胡庆雷(1979—)，男，副教授，博士生导师;

马广富(1964—)，男，教授，博士生导师.

胡庆雷，huqinglei@hit.edu.cn.

(编辑 张 宏)