非线性耦合振子间产生靶能量传递的初始条件

张也弛，孔宪仁

(哈尔滨工业大学卫星技术研究所，150080 哈尔滨)

非线性耦合振子间产生靶能量传递的初始条件

张也弛，孔宪仁

(哈尔滨工业大学卫星技术研究所，150080 哈尔滨)

针对线性振子连接非线性能量阱的系统中产生靶能量传递需要一定的初始条件，首先说明最优靶能量传递同其非保守系统中完全能量传递存在一致性，之后建立该非保守系统的慢变力学模型，并针对该系统提出引发最优靶能量传递的初始能量同系统中立方刚度存在精确比例关系的假设和推论，通过数值仿真验证了该假设及推论的正确性.最后将该结论应用于线性振子连接非线性能量阱系统的立方刚度设计，提出了设计可实现靶能量传递的立方刚度的方法.

靶能量传递;非线性耦合振子;立方刚度;非线性振动;非线性动力吸振器

动力吸振器(tuned vibration absorber，TVA)最早由Frahm于1905年提出［1］，并被广泛应用于建筑、机械等结构中.线性TVA的缺点是只在吸振器弹簧的固有频率附近有效，一旦吸振器的弹簧等部件老化或设计时弹簧刚度发生偏差，造成吸振器的固有频率偏离主结构的振动频率，就会使得吸振效率降低.Roberson［2］指出，在动力吸振器中引入非线性，可以有效的增加振动抑制的带宽，使得动力吸振器的鲁棒性显著提高.此后，非线性动力吸振器开始得到学者们的关注.

近年来，非线性能量阱(nonlinear energy sink，NES)是非线性动力吸振器的研究热点［3－10］，NES 即指用于实现靶能量传递(targeted energy transfer，TET)的非线性吸振器.靶能量传递［3］是指能量在非线性耦合振子间的高效传递现象，其特点是能量传递速度快，每次传递能量大小较精确［4］.文献［5］研究了范德波尔振子连接NES的自激振动和分岔.文献［6］对于含有非线性阻尼的NES进行了研究.文献［7］假设靶能量传递主要由1:1内共振引起，研究了两自由度线性系统连接NES的结构，在数值解与解析解比较中发现在其两个1:1内共振间存在大量次谐振.文献［8－9］对NES的减震效果进行了实验研究，验证了部分理论成果.文献［10］对能量从线性振子到非线性振子的传递及反向传递进行了研究.由于强非线性作用的影响，NES没有特定的固有频率，在靶能量传递的作用下主结构中的振动能量不可避免地传递至NES并在其中耗散.

在抑制冲击荷载产生的自由振动的过程中，NES的特性之一是对初始能量大小有较强的选择性，在初始能量小于一定值时，振动能量几乎不会传递至NES，而当初始能量远大于一定值时，在NES中耗散的能量比率也会大大降低，也就是说NES在某个大小的初始能量下效率较高，因此依据外界激励的大小进行NES的非线性刚度的调节十分必要.

本文在对保守系统中能量完全传递至NES所需的条件做简要介绍的基础上，将对非保守系统中的靶能量传递进行研究.首先研究非保守系统中的完全能量传递与最优靶能量传递关系的一致性.然后将保守系统中的完全能量传递条件推广至非保守系统，给出依据初始能量大小选择系统刚度的方法，最后通过仿真算例说明前面给出的方法是正确有效的.

1 保守系统的力学分析

考虑下面的非线性保守系统:

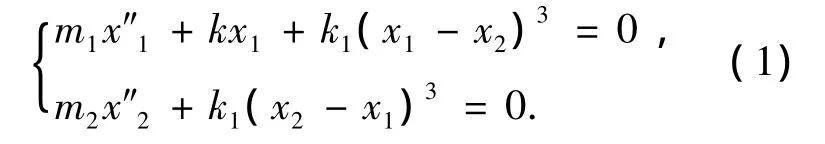
其中:m1为线性振子的质量，m2为非线性振子的质量，m2≪m1;k为线性刚度;k1为立方刚度.对上式引入新的时间尺度

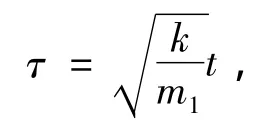
并作以下变量替换:

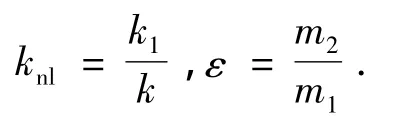
式(1)可变换为

式中˙x表示对τ的导数，ε≪1.

对式(2)作变量替换

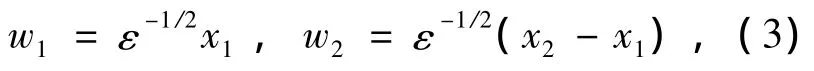
及以下复变量代换

其中 j=1，2.式(2)可写为

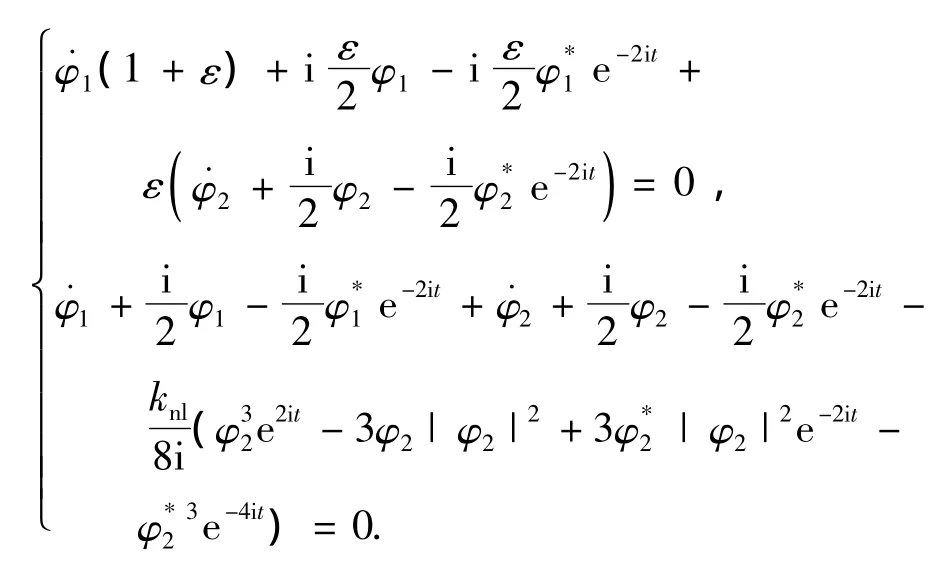
对上式进行以下多尺度展开:

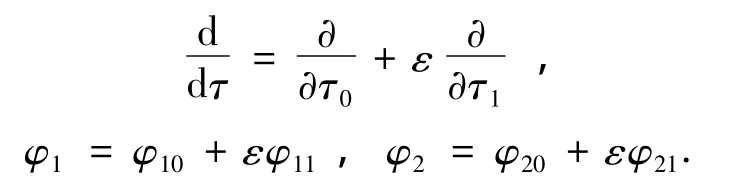
消除久期项，可得以下慢变方程［11］:

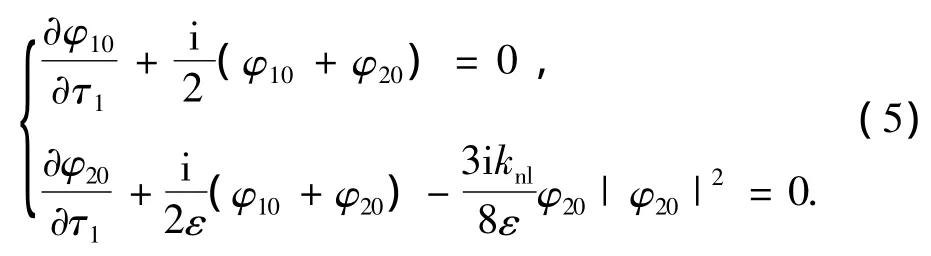
对式(5)进行如下正则变换:

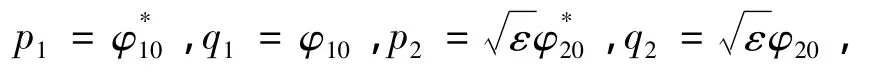
可得哈密顿量

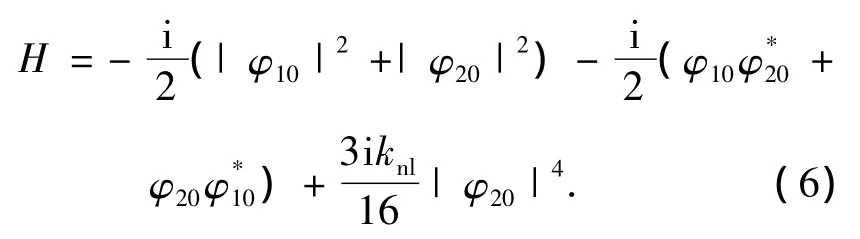
由于方程(5)满足

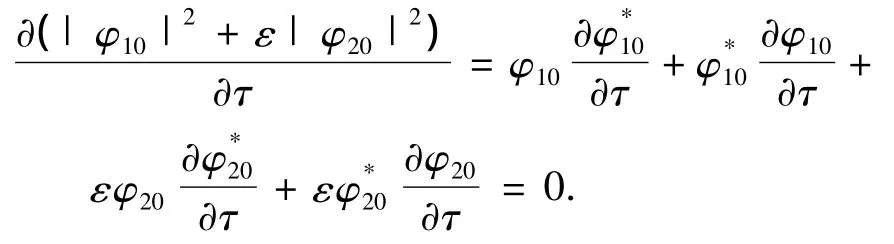
可得方程(5)的另1个首次积分

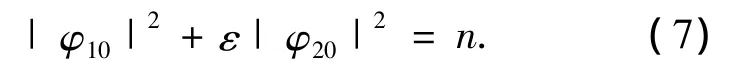
由上式可知

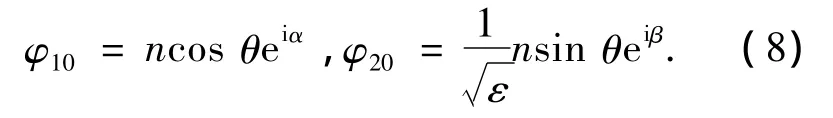
式(6)和式(7)即为方程(5)的两个首次积分.

系统(2)中线性振子的能量如下［12］:

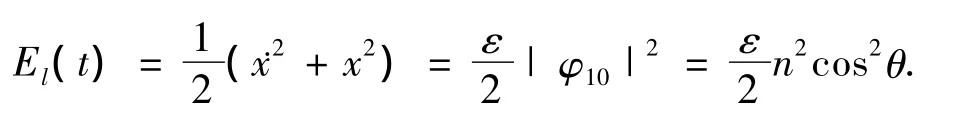
两振子间的完全能量传递可由下式表示:

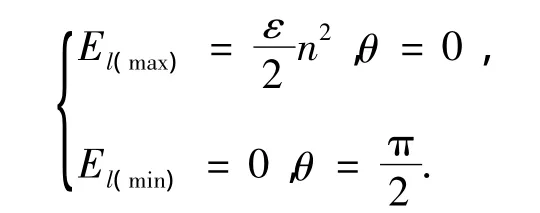
将式(8)代入式(6)，有

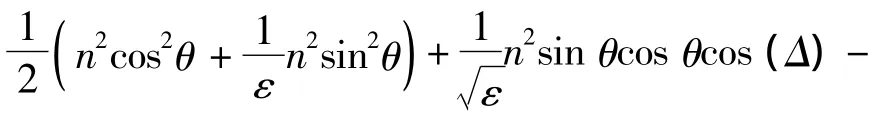
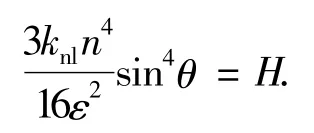
对上式做极限可表示能量完全传递至非线性振子的过程，

即

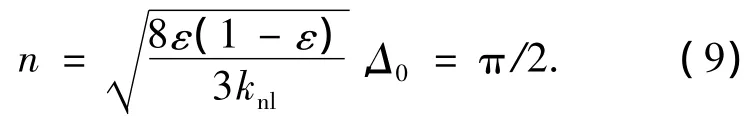
由式(3)、(4)可知线性振子的位移可表示为

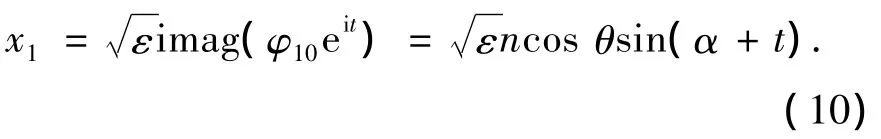
结合式(9)、(10)，当初始能量完全集中在线性振子且仅为初始位移引起时，引发两振子间完全能量传递的初始条件可写为

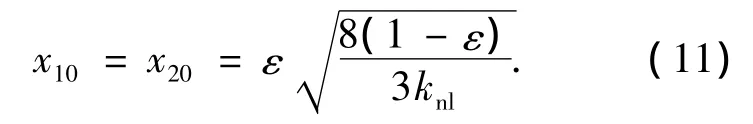
若初始能量仅为初始速度引起，可写为

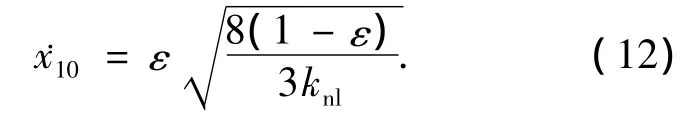
2 非保守系统的力学分析

2.1 非保守系统中的完全能量传递

对于非线性系统

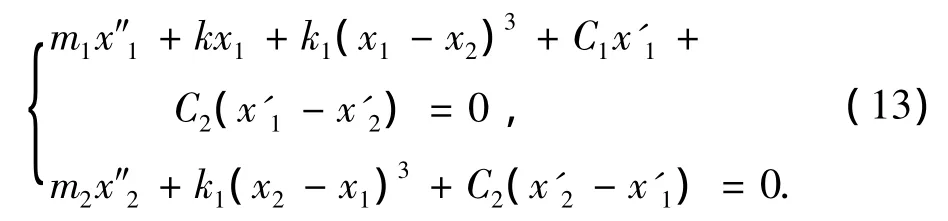
图1表示系统(13)中不同初始位移下80 s内在NES中耗散的能量比率，式中参数取m1=1，m2=0.1，k=1，k1=0.2，C1=C2=0.01，Ediss由下式计算得到

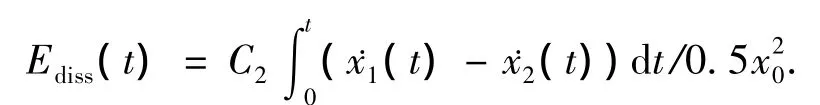
其中x0为两振子的初始位移，x10=x20=x0.由图可见NES的效率在一定的初始位移下较高，超出一定范围效率会降低，尽管选择不同参数会使得有效范围有所增大，但趋势是一致的.

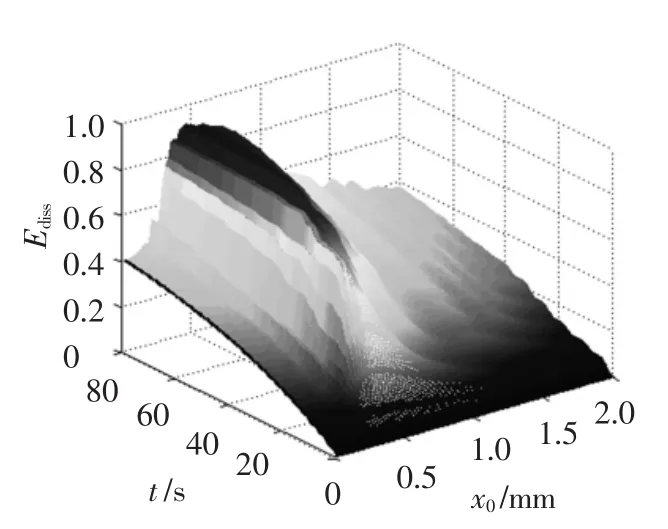
图1 初始能量在NES中的耗散比例

图2为t=80 s时在NES中耗散的能量比率，由图2可见在x0=0.42时Ediss达到最大值，NES的效率达到最高，此时两振子能量的变化曲线如图3所示，可见线性振子能量可在半个慢周期内完全传递至NES，即非保守系统中能量完全传递至NES的条件也为最优靶能量传递的条件，因此完全能量传递的研究对于NES的调制至关重要.进行NES的优化可从分析该系统中的完全能量传递入手.

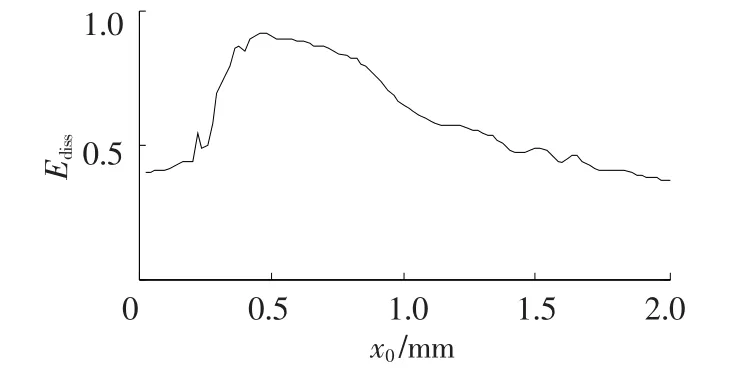
图2 t=80 s时初始能量在NES中的耗散比例

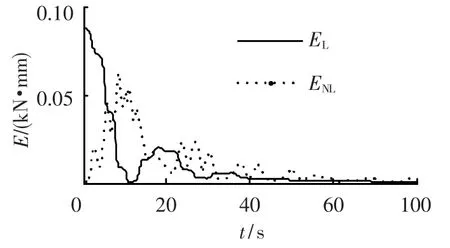
图3 两振子能量变化曲线

2.2 非保守系统的慢变力学模型

对系统(13)引入新的时间尺度并进行变量替换

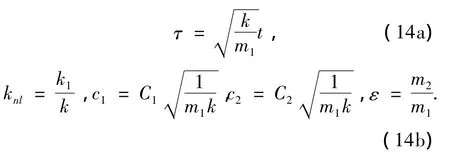
则式(13)可变换为

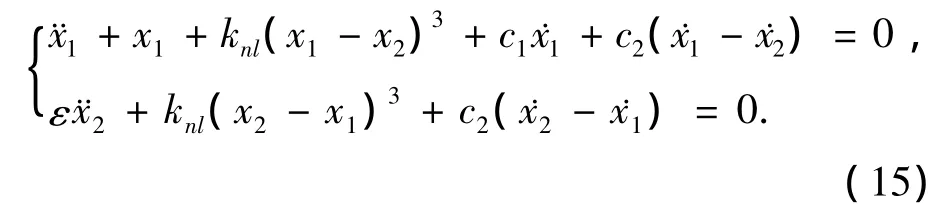
在对上述系统的内在保守系统进行研究的基础上，本节将直接对上式进行如下复变量替换:

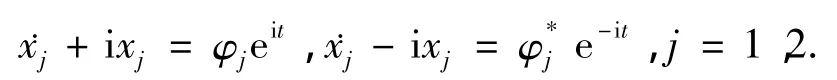
式(15)可写为

消除久期项，有

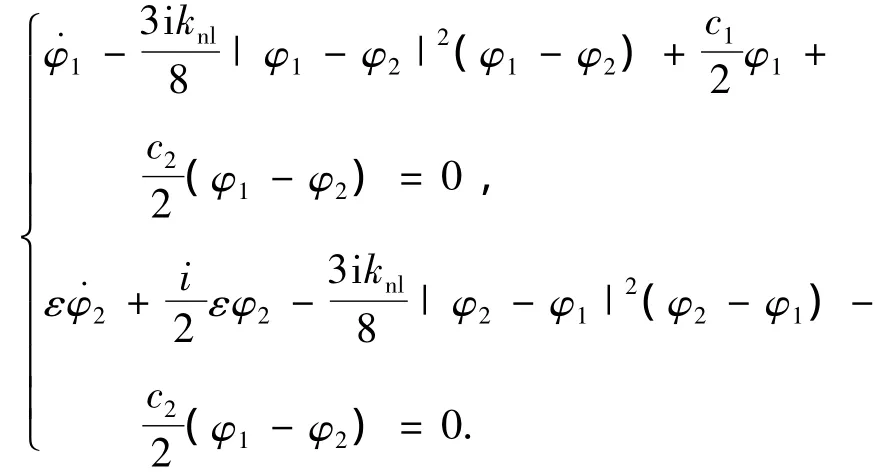
经推导易得

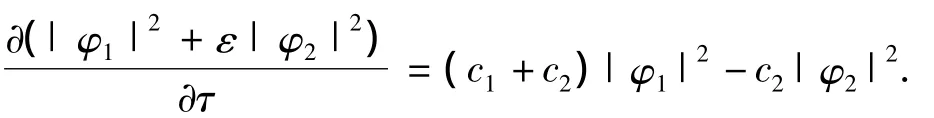
即有

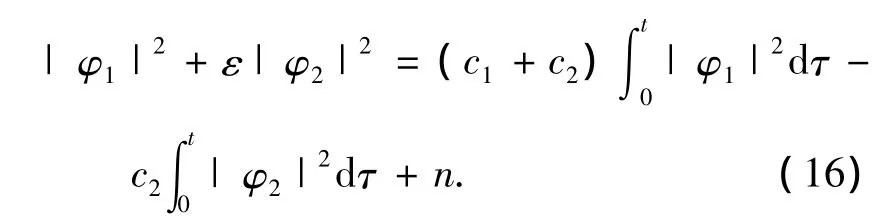
系统(15)中线性振子能量可写为

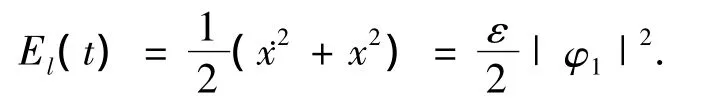
所以当φ1=0且φ2≠0时，主结构的能量完全传递至NES.

虽然非保守系统中的最优靶能量传递无法给出确切的表达式，但由式(16)可看出当阻尼c1与c2取为小量时，φ1与 φ2仍可近似表达为 φ1≈ ncos θeiα，φ2≈ nsin θeiβ.假设最优靶能量传递发生时，初始能量与刚度的关系同保守系统中是相同的(下面会给出仿真验证)，从而可由该关系进行NES中的刚度设计.

3 最优靶能量传递

3.1 最优靶能量传递与系统参数的关系

初始能量全部集中于线性振子，定义引起最优靶能量传递的初始条件为x10=X10、x20=X20、，由式(11)～(12)可知，保守系统中发生完全能量传递时:

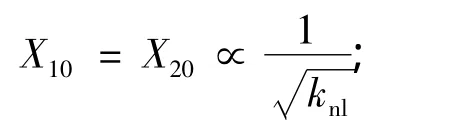
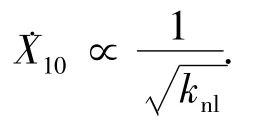
式中∝表示成正比，下面对系统(13)进行仿真计算，考察在非保守系统中上述关系是否依然成立.

由式(14)可知，knl代表主结构质量和线性刚度归一化后的立方刚度，因此尽管在下面的仿真中knl∈［0.1，9］，但其实际代表立方刚度同主结构线性刚度之比为0.1～9，因此仿真范围已经完全满足工程实际需要.

另外，通过计算初始条件在一定范围内变化时的Ediss的最大值，得到最优靶能量传递对应的初始条件，这样虽然使得下面的仿真计算量非常大，但可以准确得到在knl取某定值时引发最优靶能量传递的初始条件.

图4中ε=0.1.由图4可见引发最优靶能量传递的初始速度同立方刚度的 -0.5次方成正比.

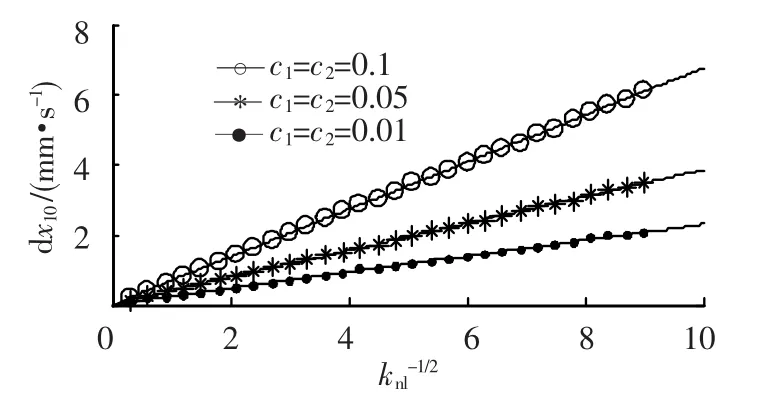
图4 引发最优靶能量传递的初始速度同系统刚度的关系

由图5可见引发最优靶能量传递的初始位移同立方刚度的－0.5次方成正比.

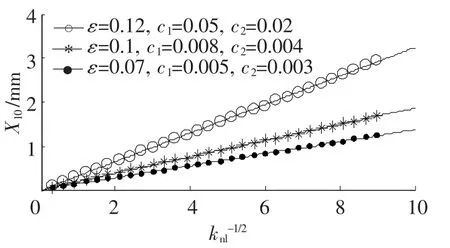
图5 引发最优靶能量传递的初始位移同系统刚度的关系

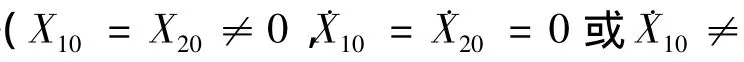
该结论可描述如下:

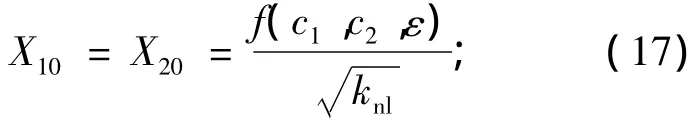
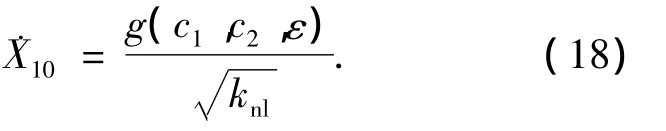
该结论中只考虑了两种特殊的初始情况，即初始能量全部由初始位移引起或全部由初始速度引起，下面将该结论推广至更一般的情形.

在系统(15)中，若式(17)、(18)成立，则有

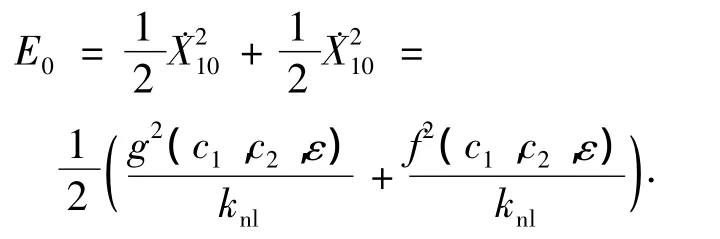
其中E0为线性主结构中可引发最优靶能量传递的初始能量.令 g2(c1，c2，ε)+f2(c1，c2，ε)=2ψ(c1，c2，ε)，则有

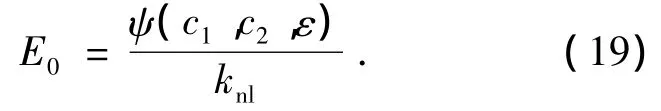
所以得到如下推论:在系统(15)中，如果初始能量全部集中于线性振子，则引发非线性吸振器中最优靶能量传递的初始能量同knl的比值成反比.

图6中初始能量同样完全集中于线性振子，但其中同时包含初始速度与初始位移.由图6可见仿真结果与理论分析完全符合，说明该推论是正确的.

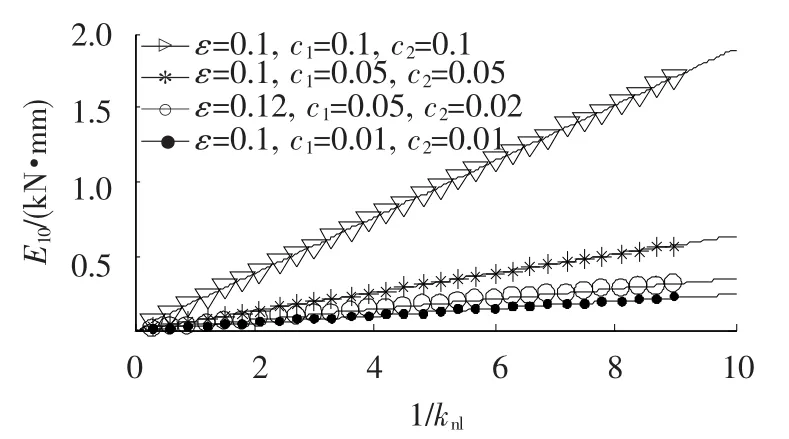
图6 引发最优靶能量传递的初始能量同系统刚度的关系

至此，本文将引发非线性吸振器中最优靶能量传递的初始条件推广到了一般情况.

3.2 初始条件变化时最优靶能量传递的确定

由式(19)可知，如果在一组系统参数下计算出 ψ(c1，c2，ε)，则该推论可用于计算 knl变化时引发最优靶能量传递的初始能量，方法如下:

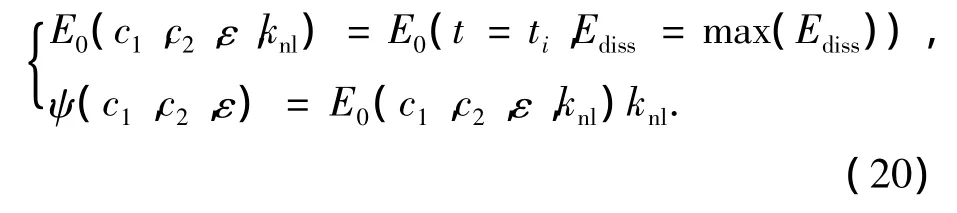
式中:ti表示系统接近稳定的某时刻.由上式中的第1个方程先确定特定参数下最优靶能量传递对应的初始能量E0，然后由第2个方程可得ψ(c1，c2，ε).则在knl取任意值时引发最优靶能量传递的初始能量都可由式(19)得到.这对于在冲击荷载下NES的调节非常重要，应用式(19)、式(20)可根据外界冲击荷载的大小方便的选取knl.

对于初始能量全部由初始速度或位移引发的两种特殊情况，有

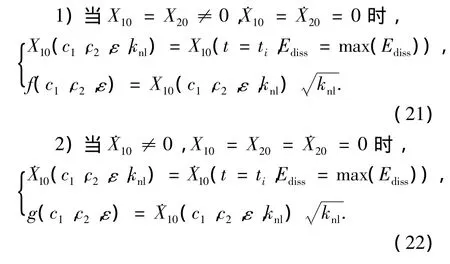
4 仿真算例

本节通过两个算例说明如何根据前文中得出的关系进行NES刚度的设计，同时本节算例的结果也验证了前面得到的结论.

例1 系统(15)中各参数设置为c1=c2=0.01，ε=0.1，初始能量全部集中于线性振子，计算knl变化时可引发最优靶能量传递的初始位移

使用式(21)，可计算得到当knl=0.1时，有f(c1，c2，ε)=0.205 5，则由式(17)可知在 knl变化时，始终有X10=0.205 5/，图7 表示由该式计算得到的引发最优靶能量传递的初始位移X10及数值仿真得到的结果的比较.

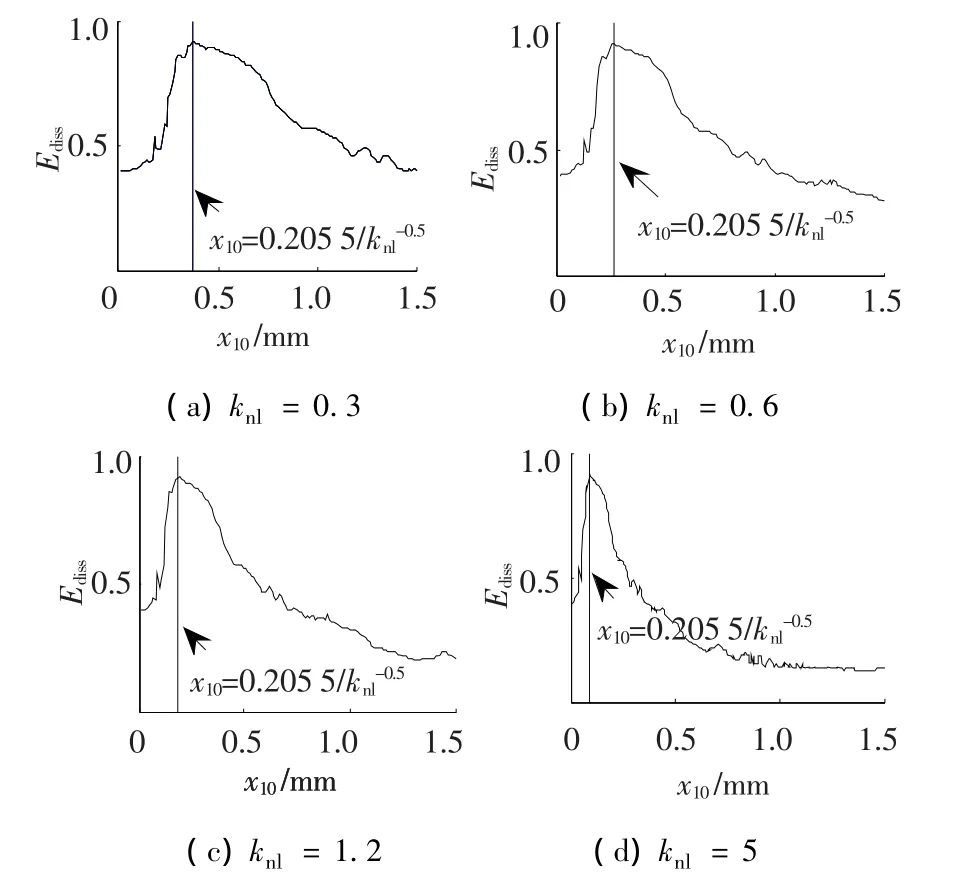
图7 不同初始位移下能量在NES中的耗散

图中取t=80 s，此时系统能量已基本耗散完毕.曲线表示Ediss随初始位移的变化，竖线表示用文中方法计算得到的引发最优靶能量传递的初始位移.由图可见该方法可准确计算出Ediss最大时对应的初始位移，说明文中方法是有效的.

例2 系统(15)中各参数设置为c1=0.008，c2=0.006，ε =0.08，计算 knl变化时最优靶能量传递对应的初始能量.

使用式(20)，首先计算得到当knl=0.2时，ψ(c1，c2，ε)=0.013 5，则由式(19)可知在 knl变化时，始终有E0=0.013 5/knl，图8表示由该式计算得的引发最优靶能量传递的初始能量E0及数值仿真得到的结果的比较.

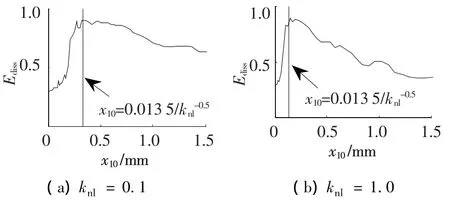
图8 不同初始能量下能量在NES中的耗散

图中取t=80 s，曲线表示Ediss随初始能量变化的曲线，竖线表示用文中方法计算得到的引发最优靶能量传递的初始能量.由图中比较可见，式(19)可精确估计knl变化时引发NES中最优靶能量传递的初始能量.

5 结论

本文通过建立非线性耦合振子的慢变近似模型并对其进行研究，建立了保守系统中的完全能量传递同非保守系统中最优靶能量传递之间的关系.研究表明在其他系统参数不变的前提下，NES中引发最优靶能量传递的初始能量同knl的大小成反比.

在以上结论基础上，本文给出了根据不同初始能量大小，调节knl使得NES产生最优靶能量传递的方法，该方法可用于设计NES中的系统刚度.数值仿真和算例表明本文的结论和方法都是正确的.

［1］FRAHM H.Device for damping vibrations of bodies:US，989958［P］.1909 －10 －30.

［2］ROBERSON R.Synthesis of a nonlinear dynamic vibration absorber［J］.Journal of the Franklin Institute，1952，254(3):205－220.

［3］KOPIDAKIS G，AUBRY S，TSIRONIS G P.Targeted energy transfer through discrete breathers in nonlinear systems［J］.Physical Review Letters，2001，87(16):165501.

［4］MANIADIS P，KOPIDAKIS G，AUBRY S.Classical and quantum targeted energy transfer between nonlinear oscillators［J］.Physica D，2004，188(3/4):153 －177.

［5］GENDELMAN O，BAR T.Bifurcations of self-excitation regimes in a Van der Pol oscillator with a nonlinear energy sink［J］.Physica D:Nonlinear phenomena，2010，239(3/4):220－229.

［6］STAROSVETSKY Y，GENDELMAN O.Vibration absorption in systems with a nonlinear energy sink:Nonlinear damping［J］.Journal of sound and vibration，2009，324(3/4/5):916－939.

［7］STAROSVETSKY Y，GENDELMAN O.Interaction of nonlinear energy sink with a two degrees of freedom linear system:Internal resonance［J］.Journal of sound and vibration，2010，329(10):1836－1852.

［8］KERSCHEN G，MCFARLAND D M，JEFFREY J K，et al.Experimental demonstration of transient resonance capture in a system of two coupled oscillators with essential stiffness nonlinearity［J］.Journal of Sound and Vibration，2007，299(4/5):822－838.

［9］LEE Y，KERSCHEN G，MCFARLAND D M，et al.Suppressing aeroelastic instability using broadband passive targeted energy transfers，part 2:experiments［J］.AIAA Journal，2007，45(10):2391 －2400.

［10］COSTA S，HASSMANN C，BALTHAZAR J，et al.On energy transfer between vibrating systems under linear and nonlinear interactions［J］.Nonlinear dynamics，2009，57(1/2):57－67.

［11］MANEVITCH L，GOURDON E，LAMARQUE C.Towards the design of an optimal energetic sink in a strongly inhomogeneous two-degree-of-freedom system［J］.Journal of Applied mechanics，2007，74(6):1078－1086.

［12］SAPSIS T P，VAKAKIS A F，GENDELMAN O V，et al.Efficiency of targeted energy transfer in coupled nonlinear oscillators associated with 1:1 resonance captures:Part II，analytical study［J］.Journal of Sound and Vibration，2009，325(1/2):297－320.

Initial conditions for targeted energy transfer in coupled nonlinear oscillators

ZHANG Ye-chi，KONG Xian-ren
(Research Center of Satellite Technology，Harbin Institute of Technology，150080 Harbin，China)

The initial conditions for targeted energy transfer in coupled nonlinear oscillators are investigated.First it is shown that optimal targeted energy transfer and complete energy exchange in non-conservative systems are basically the same in the system of a linear oscillator coupled with a nonlinear energy sink.An assumption and an inference are proposed that there is a proportional relationship between initial energy for inducing optimal targeted energy transfer and the cubic stiffness based on the research of slow-flow dynamics of the non-conservative system.The assumption and inference are verified by numerical simulations.The result can be applied for design of the cubic stiffness for inducing optimal targeted energy transfer in the system of a linear oscillator coupled with a nonlinear energy sink，and the method is also given in the paper.

targeted energy transfer;coupled nonlinear oscillators;cubic stiffness;nonlinear oscillation;nonlinear vibration absorber

O328;O322

A

0367－6234(2012)07－0021－06

2011－02－22.

长江学者和创新团队发展计划资助项目(IRT0520).

张也弛(1983—)，男，博士研究生;

孔宪仁(1961—)，男，教授，博士生导师.

张也驰，zhangyechi@hit.edu.cn.

(编辑 张 宏)