机械手空间圆弧位姿轨迹规划算法的实现

任秉银，梁兆东，孔民秀

(哈尔滨工业大学机电工程学院，150001 哈尔滨)

机械手空间圆弧位姿轨迹规划算法的实现

任秉银，梁兆东，孔民秀

(哈尔滨工业大学机电工程学院，150001 哈尔滨)

为提高机械手的空间圆弧作业任务的轨迹精度，提出采用齐次矩阵和四元数法分别进行位置和姿态的轨迹规划方法.对于位置规划，先对空间圆弧所在平面的圆心角做归一化处理，再按照平滑角速度曲线规划位置轨迹上的插值点，并用齐次矩阵表示插补点的位置，保证了插补点的位置始终在所求圆弧上.姿态规划采用四元数圆弧曲线函数以及分段三次有理插值保形样条函数实现C2连续的姿态轨迹.算例验证表明，提出的位姿规划方法能够保证机械手末端执行器的轨迹精度，在位置精度及姿态平稳过渡有较高要求的机械手的实际应用方面有推广价值.

机械手;空间圆弧;位置轨迹规划;姿态轨迹规划;四元数曲线

焊接、喷涂、装配和微操作等生产作业中广泛使用的机械手的末端执行器经常需要沿特定空间圆弧轨迹进行作业，可见空间圆弧是机械手任务空间作业轨迹的核心元素.高精度及平滑过渡的机械手空间圆弧轨迹的位姿规划的插补算法是保证机械手的末端空间圆弧轨迹精度的重要前提.对于空间圆弧轨迹的位置规划，文献［1］提出在任务空间中采用圆心角的线性插补实现空间圆弧插补的方法;文献［2］采用带误差上限的多段直线来逼近实际的圆弧;文献［3］采用修正的直线插补法以便于使所有的插补点都能落在圆弧上.上述两种采用直线逼近圆弧轨迹的位置插补方法理论上均存在偏差.在描述机械手姿态时，欧拉角和旋转矩阵存在万向节锁死、插值困难等缺陷，而四元数不存在这些缺陷，且与旋转矩阵相比，四元数在计算效率和占用计算机存储空间方面更有优势［4］.单位四元数q的集合是R3中的旋转变换群SO(3)，所以姿态规划问题可以转化为在S3空间中构造单位四元数曲线［5］.文献［6］描述的三次Bézier四元数曲线，文献［7］采用的 Hermit插值，以及文献［8］提到的Squad的规划方法都只满足C1连续.文献［9］提出的方法虽满足任意阶连续，但该方法并没有封闭解，而且会生成2i－1个中间点(i∈N+).文献［10］中的四元数圆弧能够克服两四元数圆弧曲线的连接处产生大的角加速度或者大的转矩的缺点，使两圆弧在连接处能够光滑过渡，使用2k－1次多项式满足了Ck连续性.

空间圆弧作业任务在实际插补过程中经常需要同时满足给定点的位置和姿态要求，因此作业任务前需给定空间不共线3点的齐次坐标(包括3点的旋转矩阵和空间位置坐标).

本文提出对空间圆弧在其所在平面内对应的圆心角做归一化处理，并采用平滑的S型加减速曲线进行角速度规划，采用齐次矩阵表示插补点的位置.采用四元数描述机械手末端的姿态，并通过单位四元数圆弧曲线函数以及分段三次有理插值保形函数共同实现C2连续的姿态轨迹，从而有效解决了姿态的平滑调整问题，为机械手高质量完成作业任务奠定了基础.

1 机械手空间圆弧的位置插补

1.1 空间不共线的3点所在圆弧的圆心和半径

在基坐标系下给定三维空间中任意不共线的3 点Pe(xe，ye，ze)、Pm和Ps，由该3 点确定的空间平面M1的方程表示为:Ax+By+Cz+D=0.设PePm的垂直平分面为M2，PmPs的垂直平分面为M3，则M1、M2、M3的平面方程及交点P0(x0，y0，z0)均可参照文献［1］中的方法求得，此交点P0即为Pe、Pm和Ps所确定的空间圆弧的圆心，进而可求出该圆弧的半径r.

1.2 建立所求圆弧的坐标系

以P0为原点建立圆弧所在平面的坐标系P0-UVW，令 U 轴的方向为，则 U 轴在基坐标系内的方向余弦为

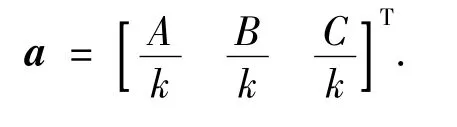
式中:

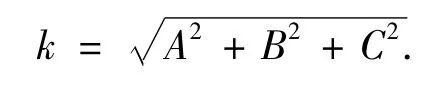
V轴方向可由右手法则确定，其方向为ο=a × n，令p= ［x0y0z0］T，则空间圆弧自身的坐标系与基坐标系之间的变换矩阵为

由变换矩阵T可将基坐标系内的空间圆弧转化为P0－UVW坐标系下的UV平面内的圆弧(如图1).

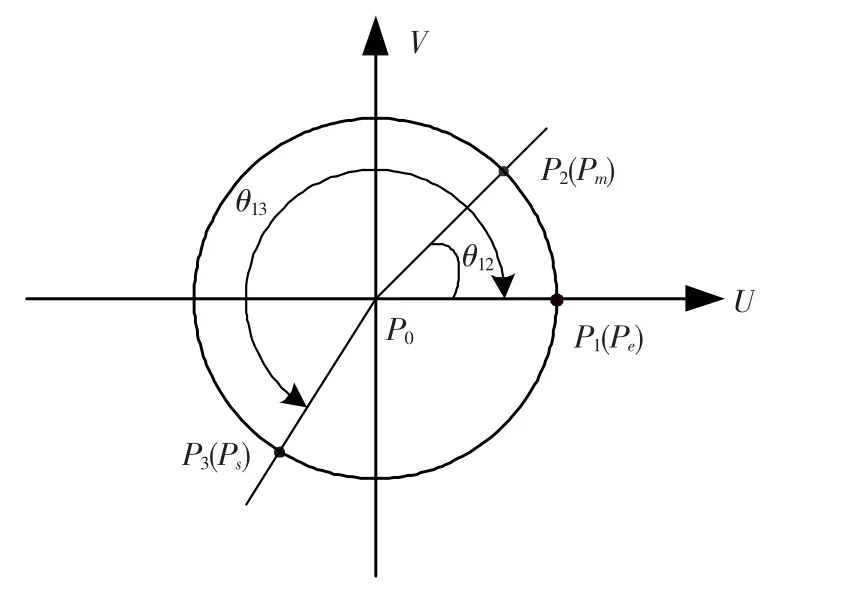
图1 空间三点决定的平面圆弧

令基坐标系内的任意一点P的齐次坐标为［x y z1］T，则P点在P0－UVW坐标系的坐标设为［x1y1z11］T，根据文献［11］，有

1.3 圆弧插补算法

针对平面圆弧所对应的角位移做归一化处理，且令各插补点对应的圆心角归一化后的参数为λ(i)，并采用S型加减速曲线对圆弧的角位移进行规划，确定插补点位置.

1.3.1 插补方向

在实际机械手的空间圆弧的任务操作中，圆弧一般具有确定的插补方向，因此本文约定在P0-UVW坐标系中UV平面内逆时针方向为其插补方向，即由Pe到Pm再到Ps的圆弧始终为逆时针圆弧.

1.3.2 插补角的大小

如图1所示，设由式(1)计算出空间3点Pe、Pm、Ps在P0-UVW坐标系下的对应点坐标为P1=(x1，y1，0)，P2=(x2，y2，0)，P3=(x3，y3，0).

在P0－UVW坐标系的UV平面内总插补角为

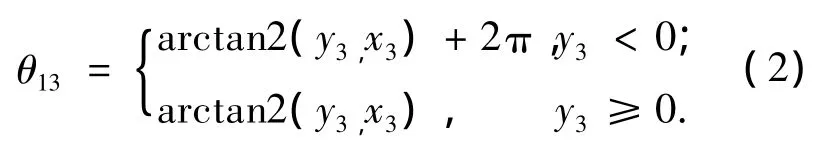
同时可求出p1、p2在P0-UVW坐标系下的平面内夹角为

1.3.3 插补次数的确定

由插补角的大小以及所采用S型加减速曲线确定插补的总时间t.本文考虑到工业机械手的精度及易于实现等要求，采用定时插补且插补周期为Ts，则总的插补次数为:

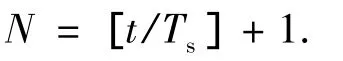
同理，可由式(3)求得θ12，进而求得由P1到P2的插补次数N12.

1.3.4 插补点的坐标

在P0-UVW坐标系的UV平面内圆弧上各插补点的坐标为

则插补点在基坐标系内的坐标为

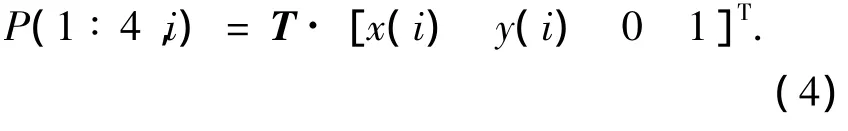
2 机械手空间圆弧的姿态插补

2.1 姿态矩阵与单位四元数的对应关系

姿态的旋转变换可以采用单位四元数描述:机械手末端执行器姿态的三维矢量绕单位轴n1旋转2β可表示为原姿态所对应的单位四元数乘以单位四元数即

将单位四元数表示为形如 q= ［s，(a，b，c)］的形式，则式中s、a、b、c与q= ［cos β，n1sin β］的对应关系为

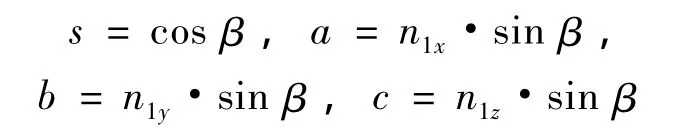
同一旋转变换可用单位四元数或姿态矩阵分别表示，且两者有明确的对应关系.与单位四元数q= ［s，(a，b，c)］对应的姿态变换矩阵为

设机械手末端姿态矩阵为

与之对应的单位四元数可表示为

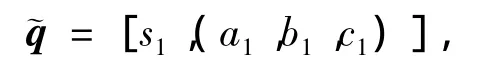
其中 s1、a1、b1、c1表达式如下:

2.2 四元数圆弧曲线的构造

2.2.1 四元数圆弧曲线插值函数

利用式(6)将Pe、Pm、Ps这3点给定的姿态矩阵转换为与其对应的单位四元数 ±q1、±q2、± q3，在八组数据中选取一组 q1、q2、q3［10］.根据文献［10］设T1为将S3∈R4中的点转换到R3空间中的3×4矩阵(T1是由q1、q2、q3和R4的原点确定的4×4正交矩阵，将R4中的点投射到R3空间，T1中存在冗余项，故文献［10］提取T1前3行使T1成为3×4矩阵即可满足要求，以下同理);为R3空间中的圆转换为R2平面中圆的2×3矩阵，为R3空间圆的圆心;S为R2平面中圆转化为R2平面中单位圆的2×2矩阵;设在单位圆上与 q1、q2、q3相对应的点为，按照式(2)和(3)方法计算出、对应圆心角α12，、对应圆心角α13，并设R2中单位圆插值圆心角为α(t)，于是可得S3空间中的四元数圆弧曲线C的表达式为

对式(7)求导(给定邻近3点的姿态矩阵为定值，对应四元数也为定值，则，S 均为定值)，可得

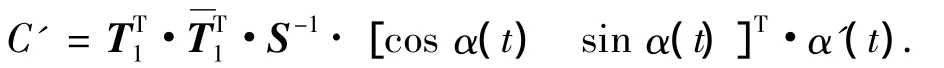
2.2.2 四元数圆弧曲线参数的有理插值函数

机械手位置插补采用定时插补，为了同时满足给定点的位置和姿态要求，则位姿插补同步进行.取机械手位置插补的次数N、N12，可得机械手姿态插补的分段时间为

即在时间［0，t1］内完成由0 到α12，在［t1，t2］内完成由α12到α13.机械手在空间圆弧的姿态插补的始末两点应有一定的速度，设α'(t)为ω(实际机械手控制应将要求的姿态速度转化为ω)，即求函数α(t)使其满足以下条件:

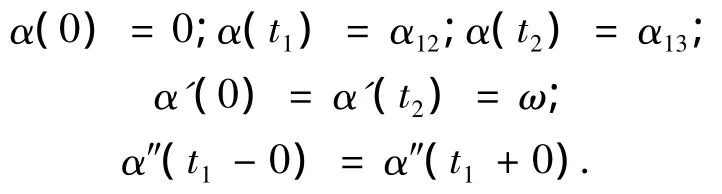
为使α(t)满足以上条件，参照文献［12］构造分段三次有理插值单调保形函数.

令 α1= α(0)，α2= α(t1)，α3= α(t2)，给定始末两点的导数值为d1=α'(0)，d3=α'(t2)，满足单调保形充分条件的d2(α'(t2))由式(8)求得［12］.

其中，ak、bk、ck可由 hk、Δk求得，hk为自变量的间距，Δk为差商;由文献［12］分析可知其隐含条件为dk＞0，但是文献中方程(8)并不能保证所求的解为正值.文献［12］中有理插值函数的C2连续的条件所推得等式为

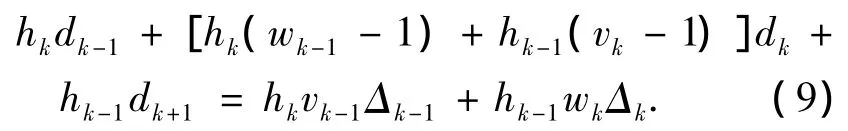
其中，wk、vk的具体表达式参照文献［12］.当式(8)所求的解d2为负值时，取其绝对值并不能满足等式(9)，此时取d2为相对于d1、d3正的无穷小，等式(9)成立，即满足C2连续的条件，同时也满足d2＞0.

通过上述方法可以求得分段三次有理插值单调保形函数α(t)，且分段函数［12］表示为:

取ti=i·Ts，i=1，2，3，…，N.将ti代入上述分段函数可以得到 α(ti)，i=1，2，3，…，N.将α(ti)代入式(7)可求得

q(i)为C2连续的单位四元数圆弧曲线表示的姿态插值离散点的函数值.目前大多数机械手在其运动卡的控制模式下的正逆解程序是依照DH法建立的关节坐标系，并采用齐次矩阵表示关节之间的相应变换关系，因此需将上述得到表示插补点姿态的四元数转化为齐次坐标矩阵，即将q(i)由式(5)转化为对应的齐次矩阵Trot(i)，并设

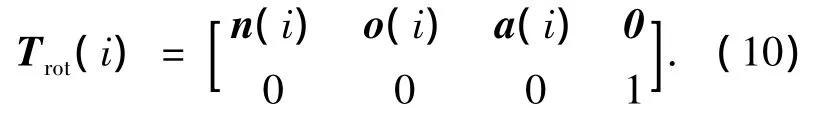
3 空间圆弧插补点的齐次坐标计算

将由式(4)得到的P(1∶4，i)和式(10)得到的Trot(i)联立可得所有插补点的齐次坐标如下:

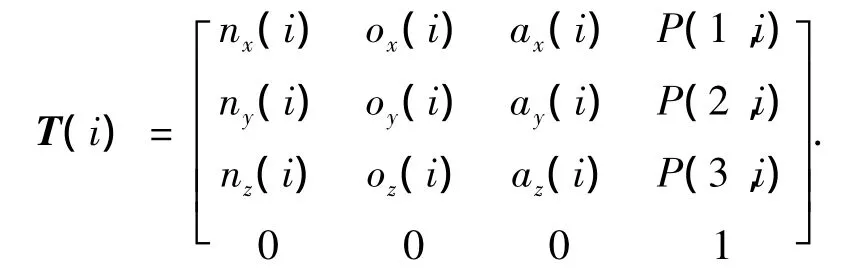
其中 i=1，2，3，…，N.

大部分的机械手为关节机械手，在实际应用中驱动的是各个关节.因此，将上述方法得到的齐次坐标通过机械手的逆运动学求得逆解，即转化为相应的关节坐标，然后通过驱动器驱动相应的关节转到一定的角度使机械手末端到达所要求的位姿.

对于各个关节，其自身插补点之间的插补运动，应依据机械手自身的精度等要求采取三次或者五次样条曲线连接插补，进而完成机械手任务空间的圆弧规划.

4 空间圆弧位姿插补仿真及分析

基于MOTORMAN－SK6弧焊机械手的几何参数，在matlab上进行了仿真实验.采用本文的机械手圆弧位置规划方法使得机械手正逆解之后所求得的插补点都在所求圆弧上(如图(2))，保证其位置的插补精度(图中3个长三维坐标序列的原点为给定Pe、Pm和Ps的空间位置，坐标序列本身为给定旋转矩阵对应的动坐标系.图中实线为Pe、Pm和Ps所确定的圆，三维坐标序列的坐标原点为运行机械手正逆解程序后所求得的插补点位置，三维坐标序列描述了姿态的渐变情况).

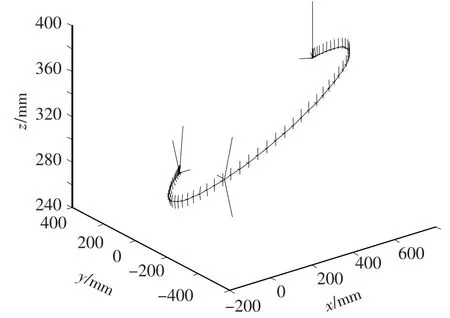
图2 空间圆弧插补位姿轨迹

由给定Pe、Pm、Ps这3点的姿态矩阵转化后的四元数和位置规划传递给姿态控制参数N、N12，并设定四元数圆弧曲线参数ω为单位速度1，控制机械手姿态的四元数圆弧曲线的参数为角位移α(t)，以及对应的角速度α'(t)和角加速度α″(t)，其曲线仿真结果分别如图3～5所示.由图(5)看出α(t)满足C2连续，由2.2.1小节的结论可知，α(t)满足C2连续则C满足C2连续，进而保证姿态插补的C2连续.

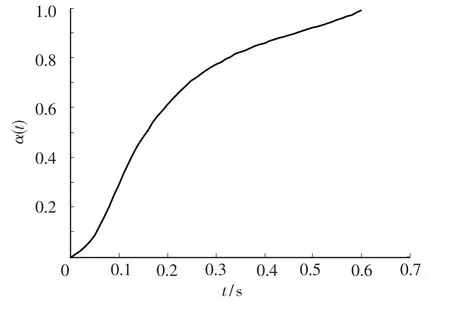
图3 四元数圆弧曲线的参数α(t)曲线

图4 α'(t)曲线

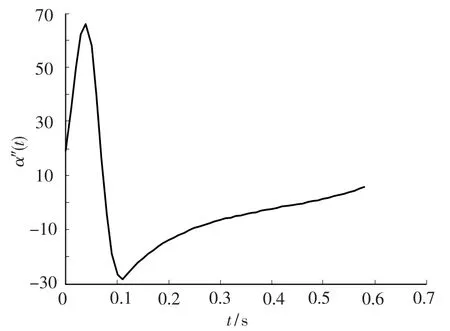
图5 α″(t)曲线

5 结论

1)本文的算法不仅能满足空间圆弧轨迹的位置精度，而且在姿态规划方面能够保证机械手姿态的C2平滑过渡，为机械手的控制及驱动提供了有效的算法，具有普遍适用的意义.

2)本文的算法通过修改可以应用在空间任意指定路径点间位姿两方面的轨迹规划，具有推广价值.

［1］吴镇炜，谈大龙.机械手空间圆弧运动的一种有效轨迹规划方法［J］.机器人，1999(1):8－11.

［2］陈国良，黄心汉，王敏.机械手圆周运动的轨迹规划与实现［J］.华中科技大学学报，2005，33(11):63 －66.

［3］叶伯生.机械手空间三点圆弧功能的实现［J］.华中科技大学学报，2007，35(8):5 －8.

［4］FUNDA J，TAYLOR R H.On homogeneous transforms，quaternions and computational efficiency ［J］.IEEE Transactions on Robotics and Automation，1990，6(3):382－388.

［5］GALLIER J.Geometric methods and applications:for computer science and engineering［M］.2nd Edition.New York:Springer Verlag，2011:281 －300.

［6］SHOEMAKE K.Animating rotation with quaternion curves［J］.Computer Graphics，1985，19(3):245 －254.

［7］NAM K W，KIM M S.Hermite interpolation of solid orientations based on a smooth blending of two great circular arcs on SO(3)［C］//Computer Graphics:Development in Virtual Enviroments.lLeeds，UK:［s.n.］，1995:171－183.

［8］DAM E B，KOCH M，LILLHOLM M.Quaternions，Interpolation and Animation［R］.［S.l.］:University of Copenhagen，1998.

［9］PLETINCKX D.Quaternion calculus as a basic tool in computer graphics［J］.Visual Computer，1989，5(1):2－13.

［10］KIM M S，NAM K W.Interpolating solid orientations with circular blending quaternion curve［J］.Computer-Aided Design，1995，27(5):385 －398.

［11］蔡自兴.机器人［M］.2版.北京:清华大学出版社，2009:25－27.

［12］SARFRAZ M.A rational cubic spline for the visualization of monotonic data［J］.Computers ＆ Graphics，2000，24(4):509－515.

An algorithm for the interpolation of circular trajectories of manipulators

REN Bing-yin，LIANG Zhao-dong，KONG Min-xiu
(School of Mechatronics Engineering，Harbin Institute of Technology，150001 Harbin，China)

To improve the arc trajectory planning accuracy of manipulators passing the non-collinear threepoints，a new approach for the manipulators’position planning and orientation planning is presented by using homogeneous matrix and quaternion respectively.For the position planning，the central angle of the arc in space is normalized，the positions of interpolation points are planed according to the smooth angular velocity curve and represented by homogeneous matrix，all the interpolation points are on the demanded arc.By using circular blending quaternion curve and a piecewise rational cubic spline together，a C2continuous orientation path which smoothly interpolates the given sequence of the manipulators positions is obtained.Simulation example shows that the presented planning approach for position and orientation can guarantee the end trajectory precision of manipulator，and can be applied to the trajectory planning of the manipulators with high accuracy requirement.

manipulator;arc in space;position trajectory planning;orientation trajectory planning;quaternion curves

TP242

A

0367－6234(2012)07－0027－05

2011－10－19.

国家科技重大专项资助项目(2011ZX04013-012).

任秉银(1966—)，男，教授，博士生导师.

任秉银，renby@hit.edu.cn.

(编辑 杨 波)