衰落信道上空频分组码的性能分析
李光球 陈素俊 余 晨 方 昕
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
引 言
正交频分复用(OFDM)技术能够将频率选择性衰落信道转化为平坦衰落信道,可有效对抗无线通信系统中的多径衰落[1-2]。将空时分组码(STBC)直接应用于OFDM系统,形成了STBC-OFDM系统[3-6]。文献[3]推导了Nakagami衰落信道上二进制相移键控STBC-OFDM系统的平均误比特率(BER)解析表达式。文献[4]推导了频率选择性Nakagami衰落信道上M进制相移键控(MPSK)STBC-OFDM系统的平均误符号率(SER)解析表达式。在空间和OFDM的不同子载波之间进行联合编码,提出了空频分组码(SFBC)-OFDM系统[7-10]。研究表明:在慢衰落环境中STBC-OFDM系统可获得与SFBC-OFDM系统相同的误码性能,但在快衰落环境中SFBC-OFDM的误码性能更好[7]。文献[8]分析了有信道估计误差的空间相关衰落信道上SFBC-OFDM系统的平均BER性能。文献[9]推导了频率选择性瑞利衰落信道上有/无信道估计误差的MPSK/方形M进制正交幅度调制(MQAM)SFBC-OFDM系统的平均BER精确及近似解析表达式。矩形MQAM是一种频谱利用率较高的数字调制技术,调制和解调又比较简单,其平均发射功率仅比最优的MQAM方案略大,方形MQAM为其特殊情况[11-14]。由于Nakagami衰落信道比瑞利衰落信道具有更大的灵活性,且瑞利衰落信道是其特殊情况[15],因此,将文献[9]瑞利衰落信道上的SFBC-OFDM系统模型推广到更为一般的Nakagami衰落信道,研究矩形MQAM调制SFBC-OFDM系统的平均误符号率性能,并推导其精确和近似解析表达式,具有重要意义,目前尚未见有研究报道。
1.系统模型

假定衰落信道满足准静态条件,即信道衰落系数在每个OFDM符号持续期间保持不变,在不同的OFDM符号之间可以独立随机变化;第i根发射天线到第k根接收天线之间的多径衰落信道脉冲响应均建模为L抽头的有限脉冲响应滤波器,i=1,2,…,nT,k=1,2,…,nR,即
(1)
式中:τl是第l个抽头的延迟扩展,αik(l)=|αik(l)|ejφik(l)(j2=-1)是第l个抽头系数,为相互统计独立的复随机变量,其相位φik(l)在[0,2π)上独立均匀分布,幅值|αik(l)|服从衰落参数和平均功率分别为ml和Ωl的Nakagami分布[15]
ml≥1/2,α>0
(2)
第i根发射天线到第k根接收天线的信道脉冲响应在第n个子载波上的频域响应可表示为[2]

(3)
式中:θik(l)=φik(l)-(2πnl/N)mod(2π).根据文献[2],可证明θik(l)对任意l均服从[0,2π)上的均匀分布。|Hik(n)|可看作L个复随机变量和的模,利用文献[2]的式(12),可得幅值|Hik(n)|的概率密度函数(PDF)的精确表达式为
(4)
式中:1F1(·;·;·)为合流超几何函数[17],J0(·)为第一类零阶Bessel函数[17]。
假定接收端已知信道状态信息,且循环前缀的长度大于最大时延。经过移去CP和进行快速傅里叶变换(FFT)后,第k根接收天线在子载波n上的接收信号为
(5)

假定采用最大似然译码,且OFDM符号的每个子载波分组均具有相同的信道增益,则对于nT根发射天线、nR根接收天线的SFBC-OFDM系统,采用最大比合并(MRC)分集接收后SFBC译码器的输出瞬时SNR为
(6)

(7)

(8)

1F1(mL-1;cL-1;dL-1t)dt
(9)
(10)
(11)
式中:I0(·)为修正的第一类零阶Bessel函数[17]。
2.精确性能分析
矩形M-QAM(M=MIMQ)信号可等效为两个正交载波上的脉冲幅度调制(PAM)信号MI-PAM和MQ-PAM的叠加。假定接收机采用匹配滤波器和相干检测,则AWGN信道上矩形MQAM信号的条件SER表达式为[14]
(12)
式中:A=1-1/MI,

(13)
于是可得SFBC-OFDM系统中采用MRC分集接收的矩形MQAM调制的瞬时SER表达式为
(14)
使用Q函数的另一种数学表达式[15]
(15)
和文献[15]的式(4.7)

(16)
将式(14)对式(7)求统计平均,并利用MGF方法,可得SFBC-OFDM系统的平均SER精确解析表达式为

=2AI1+2BI2-4ABI3
(17)
式中:
(18)
(19)

(20)
(21)
将式(8)的MGF代入式(18)、(19)和(20)可得
(22)
(23)
(24)
(25)
将式(22)~(25)代入式(17),可得具有任意抽头数的MIMO频率选择性Nakagami衰落信道上SFBC-OFDM系统平均SER的精确解析表达式。

(26)
(27)
(28)
(29)
式中:

(30)
将式(26)~(29)代入式(17),可得m1=m2=∞时等功率两抽头的MIMO频率选择性Nakagami衰落信道上SFBC-OFDM系统平均SER的精确解析表达式。
由于上述SFBC-OFDM系统的平均SER的精确计算需要计算较为复杂的数值积分,下面研究一种降低计算复杂度的近似计算方法。
3.近似性能分析
利用Q(x)的近似表达式
(31)
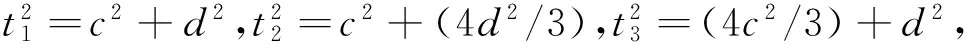
Ps≈2AJ1+2BJ2-4ABJ3
(32)
式中:

(33)

(34)


(35)
将式(8)的MGF表达式代入式(33)~(35),并利用式(21)可得
(36)
(37)
(38)
(39)
将式(36)~(39)代入式(17),可得具有任意抽头数的MIMO频率选择性Nakagami衰落信道上SFBC-OFDM系统平均SER近似表达式。

(40)
(41)
(42)
(43)
将式(40)~(43)代入式(17),可得m1=m2=∞时等功率两抽头的MIMO频率选择性Nakagami衰落信道上SFBC-OFDM系统平均SER的近似表达式。
4.仿真与数值计算结果
以16QAM和η=1的8×4QAM为例,对频率选择性Nakagami-m衰落信道上采用不同收发射天线数和不同衰落参数m值下SFBC-OFDM系统的平均SER性能进行了数值计算和仿真。在仿真中,假定OFDM子载波数为N=512,发射总功率归一化为1,平均分配给每根发射天线。对于两根、三根、四根发射天线系统,分别采用空时分组编码G2、G3、G4.假定频率选择性衰落信道的抽头数L=2,各抽头具有相同的衰落系数和平均功率。
图2给出了采用G2编码的两根发射天线单根接收天线中16QAM和8×4QAM调制SFBC-OFDM系统在不同衰落参数m值下的平均SER精确性能、近似性能及其仿真曲线。由图可知:在平均SER为10-3处,16QAM和8×4QAM调制在m=2时的平均SER性能近似值与精确值分别差大约0.4 dB和0.35 dB,该图验证了MQAM调制近似分析的准确性。

图2 不同m值下G2编码SFBC-OFDM 系统的平均SER性能(nT=2,nR=1)
图3给出了分别采用G2、G3、G4编码的16QAM和8×4QAM调制SFBC-OFDM系统在衰落参数m=8下的平均SER精确性能、近似性能及其仿真曲线。由图可知:在平均SER为10-3处,上述两种调制在G3编码时的平均SER性能近似值与精确值均约差0.35 dB.结果表明:固定接收天线数,增加发射天线数可以改善系统的平均SER性能。

图3 不同编码方案下SFBC-OFDM 系统的平均SER性能(nR=1,m=8)
图4给出了衰落参数m=8下采用G2编码的16QAM和8×4QAM调制SFBC-OFDM系统的平均SER精确性能及其近似性能。由图可知:在平均SER为10-3处,两种调制下在接收天线为2时的平均SER性能近似值与精确值均约差0.3 dB.该图验证了固定发射天线数,增加接收天线数可以改善SFBC-OFDM系统的平均SER性能。
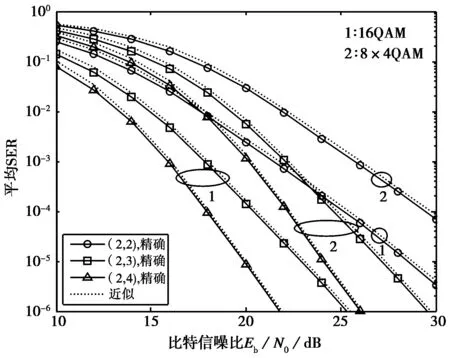
图4 在不同接收天线数下G2编码SFBC-OFDM 系统的平均SER性能(nT=2,m=8)
5.结 论
利用高斯Q函数的指数近似表达式和MGF方法推导了有任意抽头数的MIMO频率选择性Nakagami衰落信道上采用矩形MQAM调制的SFBC-OFDM系统的平均SER的精确或近似解析表达式。数值计算和仿真结果表明了理论分析的正确性和近似分析的准确性;增加接收天线数能改善系统的平均SER性能。上述结果为频率选择性Nakagami衰落信道上SFBC-OFDM系统的设计提供提供了一种有效的理论分析工具。
[1] KANG Z,YAO K,LORENZELLI F.Nakagami-mfading modeling in the frequency domain for OFDM system analysis[J].IEEE Trans Commun,2003,7(10):484-486.
[2] DU Z,CHENG J L,BEAULIEU N C.Accurate error-rate performance analysis of OFDM on frequency-selective Nakagami-mfading channels[J].IEEE Trans Commun,2006,54(2):319-328.
[3] KANG Z,YAO K,LORENZELLI F.Performance analysis of space-time block-coded OFDM over correlated Nakagami fading channels[C]∥Proc SPIE. Seattle, 2002:262-271.
[4] CHEN J,FU T,GAO X.Exact performance of OSTBC-OFDM over correlated Nakagami-mfading MIMO channels[C]∥IEEE Global Telecommu-nication Conference. San Francisco,2006:1-5.
[5] 李 卫,张小频,张 民,等.基于天线选择的自适应OFDM-STBC发射分集[J].电波科学学报,2007,22(3):453-457.
LI Wei,ZHANG Xiaopin,ZHANG Min,et al.Adaptive transmit diversity of OFDM-STBC system based on antenna selection[J].Chinese Journal of Radio Science,2007,22(3):453-457.(in Chinese)
[6] 钟 俊, 邵怀宗,彭启琮.部分信道状态信息对空时OFDM系统性能的影响[J].电波科学学报,2005,20(2):256-259.
ZHONG Jun,SHAO Huaizong,PENG Qicong.Impacti on of partial channel state information on performance of space-time OFDM system[J].Chinese Journal of Radio Science,2005,20(2):256-259.(in Chinese)
[7] LEE K F,WILLIAMS D B.A space-frequency transmitter diversity technique for OFDM systems[C]∥IEEE Global Telecommunication Conference. San Francisco,2000:1473-1477.
[8] XIA L,MAREK B.Investigations into the effect of spatial correlation on the performance of space-frequency block coded MIMO-OFDM system[C]∥IEEE Antennas and Propagation International Symposium. Hawaii,2007:2439-2442.
[9] TORABI M,AÏSSA S,SOLEYMANI M R.On the BER performance of space-frequency block coded OFDM systems in fading MIMO channels[J].IEEE Trans Wireless Commun,2007,6(4):1366-1373.
[10] 林 静,甘良才.SFBC-OFDM系统在时频双选信道下的迭代接收算法[J].电波科学学报,2009,24(1):167-173.
LIN Jing,GAN Liangcai.Iterative receive algorithm for SFBC-OFDM systems in time-frequency dispersive fading channels[J].Chinese Journal of Radio Science,2009,24(1):167-173.(in Chinese)
[11] BEAULIEU N C.A useful integral for wireless communication theory and its application to rectangular signaling constellation error rates[J].IEEE Trans Commun,2006,54(5):802-805.
[12] KARAGIANNIDIS G K.On the symbol error probability of general order rectangular QAM in Nakagami-mfading[J].IEEE Commun Lett,2006,10(11):745-747.
[13] SURAWEERA H A,ARMSTRONG J.A simple and accurate approximation to the SEP of rectangular QAM in arbitrary Nakagami-mfading channels[J].IEEE Commun Lett,2007,10(5):426-428.
[14] LEI X,FAN P,LI H.Exact symbol error probability of general order rectangular QAM with MRC diversity reception over Nakagami-mfading channels[J].IEEE Commun Lett,2007,11(12):958-960.
[15] SIMON M K,ALOUINI M S.Digital communication over fading channels[M].2ed.New York:John Wiley & Sons,2005.
[16] TAROKH V,JAFARKHANI H,CALDERBANK A R.Space-time block codes from orthogonal designs[J].IEEE Trans Inform Theory,1999,45(5):1456-1467.
[17] GRADSHTEYN I S,RYZHIK I M.Table of integrals[M].5th ed San Diego: Academic,1994.
[18] MATHAI A M,SAXENA R K.The H-function with application in statistics and other disciplines[M].New York:Wiley,1978.

