基于阵列流形分离的多输入多输出信道模型
姚 元 郑剑锋 冯正和
(清华大学电子工程系,北京 100084)
引 言
多输入多输出(MIMO)无线通信系统在收发端同时采用多根天线单元,通过利用无线信道的空间资源,可以极大提高通信容量[1]。然而,MIMO通信系统的优化设计和成功应用在很大程度上依赖于对MIMO信道复杂空时特性的深入了解。因此,MIMO信道建模成为近年来的研究热点[1-9]。
MIMO无线信道包含收发天线阵列和无线传播环境两部分,如图1所示。目前,MIMO信道模型从建模方法及范围上可以分为两大类:物理模型和解析模型[2]。物理模型对MIMO信道中的无线传播环境部分进行描述,而未包含天线阵列的影响。典型的物理模型如双方向信道模型[6-7],通过关键的物理传播参数描述无线传播环境,这些物理参数包括多径传播的路径衰减、离开角、到达角、延时等。物理模型独立于所使用的天线阵列,因此具有通用性的优点,可方便用于评估不同天线阵列配置的MIMO系统的性能。然而物理模型的复杂度往往较高,而且难以进行系统分析与设计。
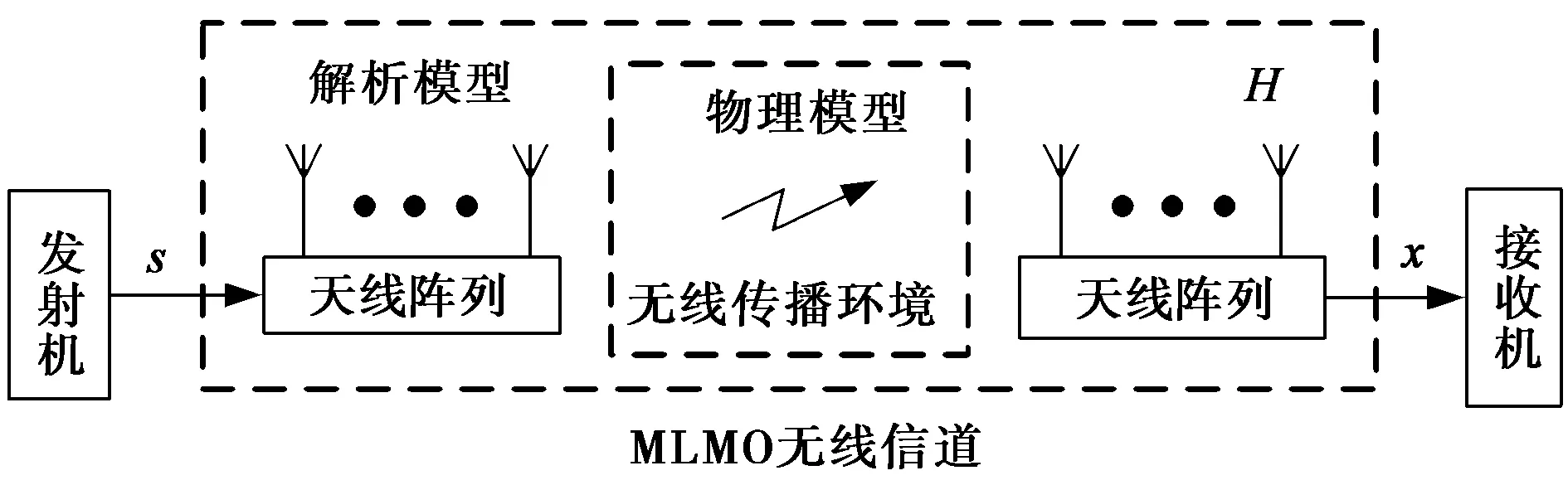
图1 MIMO无线信道及模型范围示意图
另一方面,解析模型对MIMO信道矩阵直接进行数学描述,考虑了天线阵列和无线传播环境的共同影响。典型的解析模型如基于空间相关性的随机模型[1,8-9]。解析模型能够提供MIMO信道矩阵的解析表达式,因此非常适合用于系统分析与设计,而且复杂度较低。然而,解析模型在建模时已经将天线阵列的影响考虑在内,因此其只能用于具有相同天线阵列配置的MIMO系统的分析与设计。即解析模型是天线非独立的,不具有通用性。而且,在解析模型中无法分别考察天线阵列和无线传播环境对MIMO系统性能的影响。因此,对于给定的无线传播环境,难以进行天线阵列的优化设计。图1给出了物理模型和解析模型的建模范围。
针对现有MIMO信道模型所存在的不足,拟建立一种天线独立的解析MIMO信道模型。首先通过三维阵列流形分离技术[10-12]将MIMO无线信道中的天线阵列和无线传播环境分离开来,然后利用Weichselberger模型[9]的建模思想对分离后的无线传播环境部分单独进行统计建模,得到一种天线独立的随机MIMO信道模型。所建立的模型既具有物理模型天线独立的通用性优点,可方便用于系统性能评估;又提供了MIMO信道矩阵的解析表达式,可方便用于系统分析与设计,并且复杂度较低。同时,天线阵列与无线传播环境的分离使得可以单独考察它们对MIMO系统性能的影响,并且便于研究给定无线传播环境下收发天线阵列的优化设计。
1.阵列流形分离技术
阵列流形分离技术最初由文献[10]提出,最近在阵列信号处理和测向等领域得到广泛应用[11-12]。考虑一个任意形状的N单元单极化天线阵列,其导向矢量为b(θ,φ)=[b1(θ,φ),…,bN(θ,φ)]T∈CN×1,其中CN×1表示N维复向量空间,(·)T表示转置,φ∈[0,2π)表示方位角,θ∈[0,π] 表示俯仰角。依据阵列流形分离技术,b(θ,φ)可以分解为[10-12]
b(θ,φ)=Γy(θ,φ)+ε(θ,φ)
(1)
式中:Γ∈CN×M称为采样矩阵;CN×M表示N×M复矩阵空间,采样矩阵仅依赖于天线阵列的属性,而和无线传播环境无关;y(θ,φ)∈CM×1为空间基函数向量,其和天线阵列的属性无关,M为空间基函数数目;ε(θ,φ)∈CN×1为阵列流形分解误差向量,该误差在M足够大时基本可以忽略。
在三维空间中常用球谐基函数作为空间基函数,即[10,12-13]
(2)
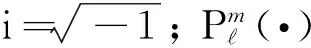
(3)
式中: (·)*表示共轭; δll′表示离散Delta函数。定义单序号ξ=2++m+1,则y(θ,φ)的第ξ个元素即为可表示为
(4)
式中L与M的关系为M=(L+1)2.
采样矩阵Γ包含了天线阵列的所有信息,如阵列单元方向图、阵列单元位置等,同时还包含了阵列单元之间的耦合、阵列制造误差等非理想特性,因此,阵列流形分离技术很适合用来描述现实中所使用的天线阵列。在实际应用中,采样矩阵Γ可以通过天线阵列的校准测量数据计算获得[10-12]。
为了简化分析,假设天线阵列单元为理想全向天线,并且不考虑天线耦合等非理想特性,则天线阵列导向矢量的第n个元素(1≤n≤N)可表示为[14]
bn(θ,φ)=exp(i2πpn·e)
(5)
式中:pn表示第n个天线阵列单元的位置矢量,该单元对波长进行归一化的球坐标为(rn,θn,φn);e表示指向(θ,φ)的单位矢量。此时,利用式(3)所示球谐基函数的正交性可计算采样矩阵Γ的第n行第ξ列元素为[10]
=4π(i)j
(6)
式中:j(·)表示第一类球贝塞尔函数。
以图2中的圆柱阵列(CA)和球阵列(SA)为例,它们的导向矢量为
bCA(θ,φ)= exp(i2π(RCAsinθcos(φ-φp)+
zqcosθ))
bSA(θ,φ)= exp(i2πRSA(sinθsinθqcos(φ-
φp)+cosθcosθq))
式中,(RCA,φp,zq)和(RSA,φp,θq)(0≤p≤P-1,0≤q≤Q-1)分别表示图2中圆柱阵列和球阵列第q层第p个天线单元对波长进行归一化的圆柱坐标和球坐标。天线阵列单元总数为N=PQ.取φp=2πp/P,zq=0.3(q-1),θq满足方程PQ(cosθq)=0,其中PQ(·)表示Q阶勒让德多项式。

图2 圆柱阵列和球阵列示意图
定义阵列流形分解的均方根误差(RMSE)为

(7)
图3给出不同天线阵列参数下圆柱阵列和球阵列的RMSE与空间基函数数目之间的关系。
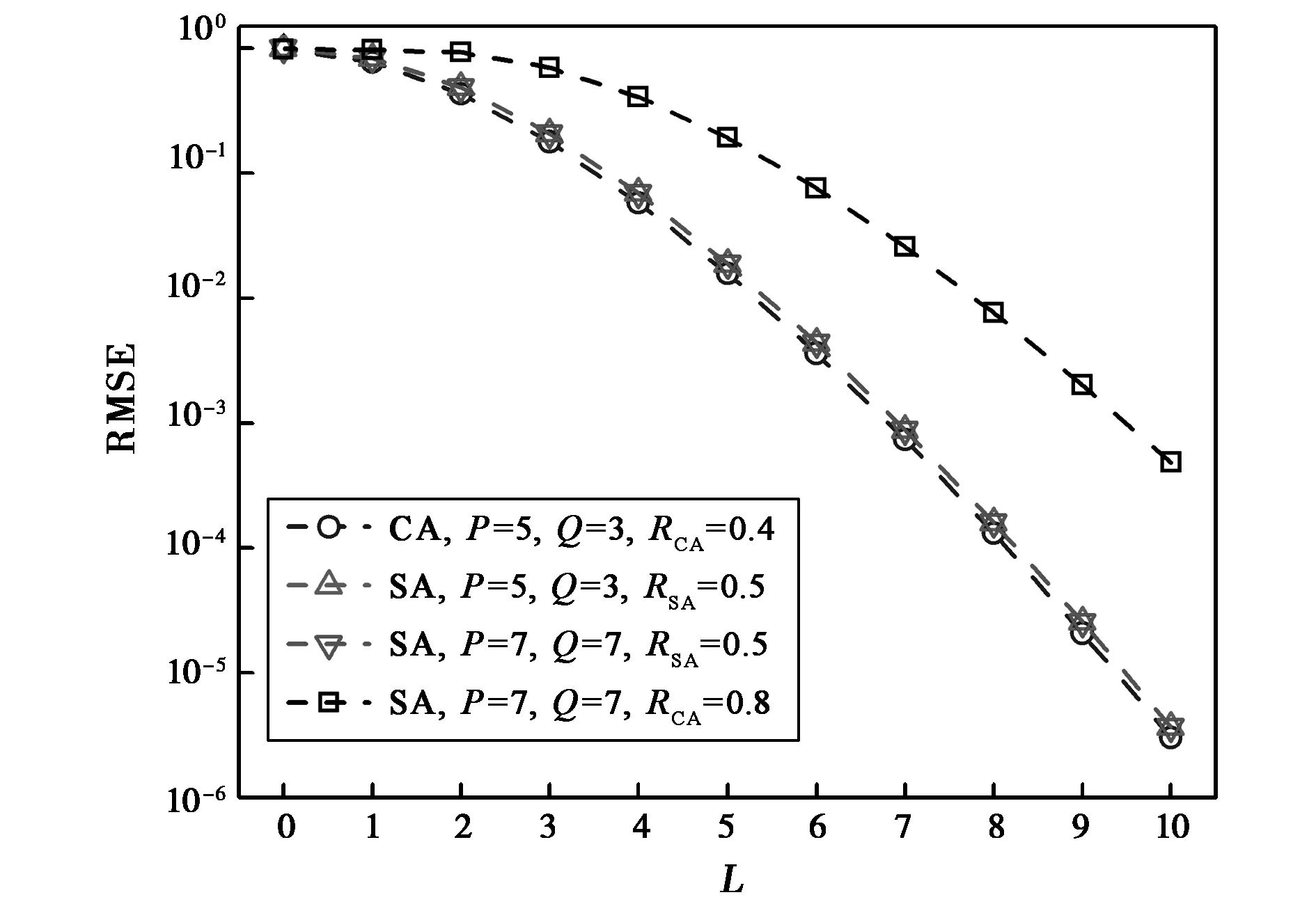
图3 不同天线阵列的建模误差与空间基函数数目的关系
由图3可知,天线阵列的建模误差随着空间基函数的增多而快速减小,在空间基函数足够多时基本可以忽略。当P=5,Q=3时,圆柱阵列的外接球半径和球阵列半径相等(都为0.5个波长),它们的RMSE曲线十分接近。当RSA=0.5时,增大球阵列单元数目并不改变其RMSE曲线,而当P=Q=7时,球阵列半径越大,同等RMSE条件下所需要的空间基函数越多。这说明在给定的阵列建模误差条件下,所需要的空间基函数数目和天线阵列的单元数目没有直接联系,而主要和天线阵列体积相关:天线阵列体积越大,同等建模误差条件下所需要的空间基函数越多。
2.信道矩阵分解
考虑如图1所示的具有NT根发射天线和NR根接收天线的单极化窄带MIMO系统,其无线信道的输入输出关系可表示为
x=Hs+n
(8)
式中:s∈CNT×1表示发射信号向量;x∈CNR×1表示接收信号向量;n∈CNR×1表示信道噪声;H∈CNR×NT表示联系发射信号和接收信号的信道响应矩阵,它表征了MIMO无线信道的特性。
在双方向模型中,MIMO信道矩阵H被视为多条传播路径的线性叠加,其可表示为[6-7]
(9)
式中:αl、(θT,l,φT,l)和(θR,l,φR,l)(1≤l≤Lpath)分别表示第l条传播路径的复数衰减、离开角和到达角,Lpath为多径数目;bT(θ,φ)和bR(θ,φ)分别表示发射和接收天线阵列的导向矢量; (·)H表示共轭转置。
依据式(1)所示的阵列流形分离技术,并且假设空间基函数数目足够大,则忽略天线阵列建模误差后收发天线阵列的导向矢量可表示为
(10)
式中:ΓT∈CNT×MT和ΓR∈CNR×MR分别表示发射和接收天线阵列所对应的采样矩阵;yT(θ,φ)∈CMT×1和yR(θ,φ)∈CMR×1为类似式(4)所示的球谐基函数向量,并且有MT=(LT+1)2,MR=(LR+1)2.
由于采样矩阵ΓT和ΓR与无线传播环境无关,将式(10)代入式(9)可得
(11)
式中矩阵H0∈CMR×MT为
(12)
由式(11)可知,利用阵列流形分离技术可将MIMO信道矩阵H分解为两部分:一部分为发射和接收天线阵列所对应的采样矩阵ΓT和ΓR,其仅依赖于天线阵列的属性,而和无线传播环境无关,对于给定的天线阵列而言,它们是常数矩阵;另一部分为矩阵H0,其和收发天线阵列的属性无关,而仅与随机的无线传播环境相关,表征的是无线传播环境的固有特性。对比式(9)和式(12)可将矩阵H0理解为球谐函数各模式之间的无线信道响应矩阵。因此,利用三维阵列流形分离技术,实现了MIMO无线信道中天线阵列和无线传播环境的分离。
3.天线独立的随机MIMO信道模型
3.1 基于空间相关性的随机模型
基于空间相关性的随机MIMO信道模型假设信道矩阵H的元素为联合多元高斯分布。此时,矩阵H各元素之间的相关性,即全相关矩阵R可以完全描述信道矩阵H的统计特性
R=E[hhH]∈CNTNR×NTNR
(13)
式中:E[·]表示取平均;h=vec(H)∈CNTNR×1表示将信道矩阵H各列堆叠形成的列向量,vec(·)表示矩阵向量化。
将式(11)代入式(13),并利用矩阵向量化的性质:vec(ABC)=(CT⊗A)vec(B),其中⊗表示矩阵的Kronecker积,可得

(14)

由式(14)可知,全相关矩阵R是矩阵R0的线性变换,该变换关系由收发天线阵列的采样矩阵共同决定。一旦确定了矩阵R0便可以确定MIMO信道的全相关矩阵R。因此,空间相关性的建模思想同样可用来描述天线独立的随机矩阵H0.
在传统基于空间相关性的随机MIMO信道模型中,Weichselberger模型[9]在复杂度和准确度之间取得了较好折中,与信道测量结果吻合较好,因此,借鉴该模型的建模方法对矩阵H0进行统计描述。定义发射和接收模式相关矩阵为[2,9]
(15)
式中:UT∈CMT×MT,UR∈CMR×MR为酉矩阵,它们的列向量分别为矩阵RT和RR的特征向量;ΛT∈CMT×MT和ΛR∈CMR×MR为对角矩阵,它们的对角元素分别为矩阵RT和RR的特征值。则天线独立的随机矩阵H0可表示为
(16)
式中:矩阵G∈CMR×MT的元素为零均值单位方差的复高斯随机变量; 矩阵Ω是MR×MT的非负实矩阵,其元素表征了无线传播环境收发端各特征模式之间的功率耦合关系。矩阵Ω满足下列等式
(17)
式中⊙表示矩阵Hadamard积。
最后,将式(16)代入式(11)中,可得到一种天线独立的随机MIMO信道模型
(18)
3.2 模型参数讨论
在所建立的模型中,需要确定的参数包括仅与收发天线阵列相关的确定性参数MT、MR、ΓT和ΓR,以及仅与无线传播环境相关的统计参数UT、UR和Ω,下面对这些参数依次进行讨论。
由前文分析可知,MT和MR主要和天线阵列体积相关。在给定的天线阵列建模误差条件下,阵列体积越大,所需要的空间基函数越多。在实际应用中,可以利用数值方法来确定MT和MR的最小取值,以使得天线阵列建模误差在允许范围之内。增大MT和MR可以提高信道模型的准确度,但是模型的复杂度也随之提高。
矩阵ΓT和ΓR作为发射和接收天线阵列的采样矩阵,对于给定的天线阵列,它们是常数矩阵。对于理想的天线阵列,采样矩阵各元素表达式如式(6)所示;而对于实际的非理想天线阵列,采样矩阵可以通过天线阵列的校准测量数据计算获得[10-12]。
由式(15)和(17)可知,天线独立的矩阵UT、UR和Ω都可由矩阵H0计算获得,而矩阵H0可由式(12)计算。式(12)中各物理传播参数的统计分布既可以通过实际测量结果获得,也可以从现有物理模型[2-7]中获得。
3.3 模型复杂度以及天线独立性
在模型复杂度方面,仅需要考虑和随机无线传播环境相关的模型参数,即矩阵UT、UR和Ω的元素数目。Weichselberger模型所需要的实参数数目为NT(NT-1)+NR(NR-1)+NTNR.类似的,新模型需要MT(MT-1)+MR(MR-1)+MTMR个实参数。因此,当空间基函数数目M比天线阵列单元数目N小时,单次仿真中新模型复杂度比Weichselberger模型更低,否则后者更优。由前文分析可知,M主要和天线阵列体积相关,而和天线单元数目N没有直接联系。因此,如果在给定体积内放置较少的天线单元,则新模型复杂度比Weichselberger模型高,如果在给定体积内放置了大量密集的天线单元,则新模型将更加有效。
当利用模型考察给定无线传播环境下不同MIMO系统的性能,则新模型更具优势。这是因为一旦系统更换了所使用的收发天线阵列,Weichselberger模型就需要重新计算模型参数。而对于给定的无线传播环境,新模型仅需要计算一次模型参数,当所使用的天线阵列特性发生改变,则只需要替换相应的采样矩阵。这使得新模型具有像物理模型一样的通用性优点。
在系统的分析与设计方面,Weichselberger模型对信道矩阵H直接进行统计建模,已经将天线阵列和无线传播环境的共同影响考虑在内,因此,对于给定的无线传播环境,无法进行天线阵列的优化设计。而新模型实现了天线阵列与无线传播环境的分离,可以依据随机无线传播环境的统计信息,对天线阵列的采样矩阵进行相应的调整与设计,以优化MIMO系统某一项指标,如分集增益或者平均信道容量等[15]。
4.数值仿真结果
为了验证所建模型的正确性和有效性,进行了数值仿真实验。为了简便,假设发射和接收天线阵列相同,故有NT=NR=N,MT=MR=M.
选取MIMO信道容量作为评估准则。当发射端不具有信道状态信息,将功率均匀分配给各发射天线时,MIMO信道容量为[1]
(19)

为了进行广泛比较,选取了典型室内、3GPP SCME标准模型的城市微小区[16]和ITU标准模型的郊区非视距宏小区[17]三种场景。在典型室内环境中假设存在5个散射体簇,各散射体簇所对应的平均离开和到达方位角在0至360°内均匀分布;每个散射体簇内含有20个多径分量,这些传播路径的离开和到达方位角在簇内呈Laplacian分布,Laplacian分布的角度扩展为26°.这些无线传播环境参数与典型室内环境的测量结果相吻合[2-7]。而城市微小区和郊区非视距宏小区的无线传播环境参数则分别依据文献[16]和[17]进行设置。此外,假设所有多径的离开和到达俯仰角在60°至90°内均匀分布,各路径增益呈零均值高斯分布。
分别考察采用如图2所示的圆柱阵列和球阵列的两种MIMO系统,并取P=5,Q=3,RCA=0.4,RSA=0.5,L=4.对典型室内环境,依据上述无线传播环境参数,由式(9)和(12)分别产生104个信道矩阵H和H0的随机样本,并利用这些样本计算Weichselberger模型和新模型的统计参数,信道矩阵H的随机样本同时被用来计算真实信道容量的累积概率分布(CDF)。然后利用Weichselberger模型和新模型分别随机生成104个信道矩阵H的样本来估计真实信道容量的CDF.而对于城市微小区和郊区非视距宏小区场景,则分别计算SCME标准模型和ITU标准模型所对应的信道容量CDF,并与新模型的预测结果相对比。
图4显示出室内环境下上述两种MIMO系统的真实信道容量CDF曲线和不同MIMO信道模型的估计结果。图5和图6分别给出城市微小区和郊区非视距宏小区场景下各标准化模型的信道容量CDF曲线和新模型的预测结果。

图4 典型室内不同MIMO系统信道容量CDF曲线

图5 城市微小区不同MIMO系统信道容量CDF曲线

图6 郊区非视距宏小区不同MIMO系统 信道容量CDF曲线
由图4可知,Weichselberger模型和新模型均可以准确预测室内真实信道容量的统计分布,两者的估计准确度相当。而图5和图6则说明新模型的结果和各标准化模型的结果十分相近,进一步验证了新模型的正确性。而在上述仿真中,Weichselberger模型、SCME标准模型和ITU标准模型都需要针对不同的MIMO系统重新计算生成模型参数,而新模型仅计算了一次模型参数:当天线阵列改变时,新模型仅需要更换相应的采样矩阵。因此,新模型较这些模型更方便用于具有不同天线阵列配置的MIMO系统的性能评估。
5.结 论
利用三维阵列流形分离技术建立了一种天线独立的解析MIMO信道模型,该模型既具有物理模型通用性的优点,又提供了信道矩阵的解析表达式,复杂度较低,可方便用于MIMO系统的分析设计与性能评估。
[1] FOSCHINI G J,GANS M J.On limits of wireless communications in a fading environment when using multiple antennas[J].Wireless Personal Commun,1998,6(3):311-335.
[2] ALMERS P,BONEK E,BURR A,et al.Survey of channel and radio propagation models for wireless MIMO systems[J].EURASIP Journal on Wireless Communication and Networking,2007,56(1):1041-1049.
[3] 张 蕊,张利军,原梦钰,等.多输入多输出宽带时变信道分布散射模型研究[J].电波科学学报,2011,26(1):73-77.
ZHANG Rui,ZHANG Lijun,YUAN Mengyu,et al.Distrubuted scattering model for MIMO wideband and time-variation channel[J].Chinese Journal of Radio Science,2011,26(1):73-77.(in Chinese)
[4] 魏明东,张云峰,张业荣,等.基于独立AOA和AOD的宽带MIMO信道建模及仿真[J].电波科学学报,2010,25(5):871-875.
WEI Mingdong,ZHANG Yunfeng,ZHANG Yerong,et al.Modeling and simulation of wideband MIMO channels based on independent AOA and AOD[J].Chinese Journal of Radio Science,2010,25(5):871-875.(in Chinese)
[5] 肖海林,聂在平,杨仕文. 室内MIMO无线信道:模型和性能预测[J].电波科学学报,2007,22(3):385-389.
XIAO Hailin,NIE Zaiping,YANG Shiwen.Indoor MIMO wireless channels:models and performance prediction[J].Chinese Journal of Radio Science,2007,22(3):385-389.(in Chinese)
[6] STEINBAUER M,MOLISCH A F,BONEK E.The double-directional radio channel[J].IEEE Antennas Propag Mag,2001,43(4):51-63.
[7] MOLISCH A F,ASPLUND H,HEDDERGOTT R,et al.The COST 259 directional channel model-I.overview and methodology[J].IEEE Trans on Wireless Comm,2006,5(12):3434-3449.
[8] KERMOAL J P,SCHUMACHER L,PEDERSEN K I,et al.A stochastic MIMO radio channel model with experimental validation[J].IEEE J.Sel Areas Comm,2002,20(6):1211-1226.
[9] WEICHSELBERGER W,HERDIN M,ÖZCELIK H,et al.A stochastic MIMO channel model with joint correlation of both link ends[J].IEEE Trans on Wireless Comm,2006,5(1):90-100.
[10] DORON M A,DORON E.Wavefield modeling and array processing,part I,part II,and part Ⅲ[J].IEEE Trans Signal Process,1994,42(10):2549-2580.
[11] BELLONI F,RICHTER A,KOIVUNEN V.DoA estimation via manifold separation for arbitrary array structures[J].IEEE Trans Signal Process,2007,55(10):4800-4810.
[12] COSTA M,RICHTER A,KOIVUNEN V.Unified array manifold decomposition based on spherical harmonics and 2-D Fourier basis[J].IEEE Trans Signal Process,2010,58(9):4634-4645.
[13] ARFKEN G,WEBER H J.Mathematical Methods for Physicists[M].San Diego:Academic,2001.
[14] VAN TREES H L.Optimum Array Processing(Detection,Estimation,and Modulation Theory,Part IV)[M].New York:Wiley,2002.
[15] QUIST B T,JENSEN M A.Optimal antenna radiation characteristics for diversity and MIMO systems[J].IEEE Trans Antennas Propag,2009,57(11):3474-3481.
[16] 3rd Generation Partnership Project.Spatial Channel Model for Multiple Input Multiple Output(MIMO)Simulations[R/OL].[2011-04-15].http∥www.3gpp.org/ftp/Specs/html-info/25996.htm.
[17] International Telecommunication Union.Guidelines for Evaluation of Radio Interface Technologies for IMT-Advanced[R].Geneva:ITU,2008.

