电磁环境仿真中电波传播模型研究及仿真分析
张文波 曹耀钦
(第二炮兵工程大学,陕西 西安 710025)
引 言
飞行器控制通信仿真中,仿真主体与客体之间大多采用无线电波通信作为控制通信的主要手段,而仿真主体与客体之间的电波损耗预测仿真是飞行器电磁环境仿真的重要任务。在飞行器无线控制通信系统设计和发射之前需要对其飞行轨迹上的电波损耗进行仿真预测,以便于操作人员在必要时进行调校。由于执行任务的需要,飞行器的飞行路径经常会选择在多山地区上空,这就导致了飞行器控制无线通信信道的地形环境非常复杂,给飞行器控制的精确性带来挑战。同时,飞行器飞行速度快,控制通信时间不能与预测或理论时间相差较大。因此,飞行器通信信道损耗预测模型需要满足以下需求:
·预测精度高
·仿真时间短
·适用于复杂地形
1.传播模型分析及建模
1.1 传播模型的分析与选择
飞行器从起飞到飞临目标上空,一般情况下可能会途经平原、丘陵、高山、河流甚至是海洋等不规则地形,对通信信道损耗的预测需要考虑不同的天然地形环境的影响。同时还要考虑树木、建筑物和其他遮挡物等人为因素的影响。电波传播预测模型大体可分为两类:一类是基于电磁波传播理论,根据具体的适用环境,确定电磁环境的边界条件,求解麦克斯韦电磁波方程式,进而确定出电磁波的传播路径和传播场强值,该类模型通常适用于计算近区场电磁传播,而对远区场而言边界条件难以确定,需要考虑的因素增多,计算相当复杂;另一类是利用数理统计方法,通过将大量数据筛选后进行统计分析,并结合部分电磁理论来确定对电磁波传播损耗影响较大的因素,再利用数据拟合等方法得到电磁波的传播预测模型,属半经验模型,对远区场的电磁波预测大都使用该类模型。
通过长期的测试、研究,人们总结归纳了多种适用于远距离的电波传播预测模型,如Okumura-Hata模型[1]、Egli模型和Longley-Rice模型等。
Okumura模型以准平坦地形大城市区的中值场强或路径损耗作为参考,在工程实际中多用于市区、郊区和开阔地等地形起伏不大的地区。对于起伏较大的不规则地形,如丘陵地形、水陆混合地形和孤立山峰,其传播损耗应在准平坦地形的中值传播损耗的基础上,加上适当的修正因子进行校正。Okumura模型以曲线图的形式给出,不便于快速的仿真,而Okumura-Hata模型[2]是Hata在Okumura曲线图的基础上,通过曲线拟合所作的经验公式[3]:
L= 69.55+26.16lgf-13.82lght-
A(hr)+(44.9-6.55lght)(lgd)γ+Loss′
式中:f为电波频率,单位MHz;d为通信距离,单位km;ht,hr为收发天线高度,单位m;Loss′为地形修正因子,A(hr) 是移动天线有效高度修正因子,单位dB;γ为距离修正因子。
Egli模型[4]是通过在VHF频段和UHF频段对不规则地形上得到的大量实测数据综合分析的基础上提出的一种经验模型,以地形起伏和障碍物高度不超过15 m为准,对于地形起伏和障碍物超过15 m的,运用修正因子加以修正。该模型仅适用于视距范围内。
Longley-Rice模型[5-6]被称为不规则地形模型,以电波传播理论为依据,结合丰富的实测数据,用以预测在自由空间中由地形的非规则性造成的中值传播损耗。该模型具有两种预测模式。当能够获取详细的地形剖面数据时,可以采用点对点模式,如果没有地形数据,预测模型需要估算与路径相关的参数,需采用区域模式。
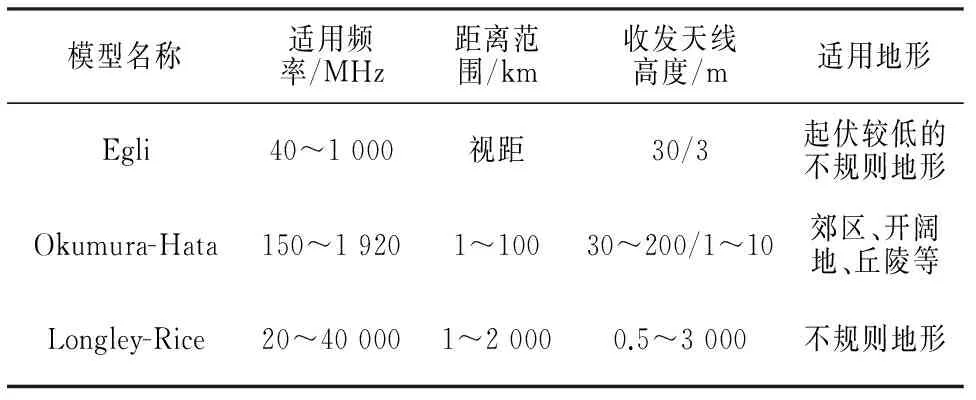
表1 不同传播预测模型的适用范围
表1描述了以上三种模型的具体适用范围。从表中可以看出:Egli模型的适用频率范围较窄,距离范围仅为视距,Egli模型不适用于地形高度起伏太大的山区,而Okumura-Hata模型和Longley-Rice模型均可用于飞行器通信仿真系统。对这两种预测模型在开阔地和起伏较大的丘陵地区进行仿真,如图1和图2所示。

图1 开阔地传播损耗对比

图2 丘陵地区传播损耗对比
图1中,Longley-Rice模型的预测值比Okumura-Hata模型的预测值明显偏低。Okumura-Hata模型在两种地形下的预测值变化较小,丘陵地区仅比开阔地偏高20 dB左右,而Longley-Rice模型的变化较大,丘陵地区比开阔地高30 dB左右。从仿真可以看出:Longley-Rice模型比Okumura-Hata模型对地形的变化更加敏感,特别是图2中Longley-Rice模型的点对点模式能够实时地反映地形对电磁波传播的影响,比区域模式更加适用于传播地形复杂的飞行器通信信道预测。
文献[3]和[8]中均使用了Longley-Rice模型作为海面电波传播模型,但由于应用环境是海洋,地形不规则度较小,因此,使用的是区域模式;文献[7]中提出使用Longley-Rice模型作为地面和导弹通信信道模型,在区域模式下仿真了频率、地形、气候类型和天线位置对电波传播衰减的影响,但未给出点对点模式下地形影响的仿真结果。本文通过抽取传播路径地形高程值,从以飞行器高度作为接收天线高度的角度,使用点对点模式对电波传播衰减进行了仿真。
1.2 Longley-Rice模型建模
Longley-Rice模型引入了电磁波频率f、收发天线有效高度he1、he2及位置、极化方向、地形不规则度Δh、地球表面折射率Ns、地面电导率σ和相对介电常数εr等因素,在考虑电波本身特性的基础上,同时兼顾了传播环境的电气特性。不同路径长度的传播损耗参考中值Aref的计算如下[6]
(1)
式中:d为传播距离;dLS为光滑地面距离;dx表示此处的衍射损耗和散射损耗相等;Ae、Aed、Aes分别表示自由空间下视距、衍射和散射时的传播损耗值;K1和K2为传播损耗系数;md和ms分别为衍射和散射损耗系数。
通过式(1)可以分别计算视距传播损耗、衍射传播损耗和散射传播损耗。同时,再考虑到自由空间传播损耗,整个传播路径上的总体损耗为
A=Aref+Afree
(2)
式中:Afree=32.45+20lgd+20lgf
(3)
d为传播距离(km);f为电波频率(MHz)。
1) 衍射传播损耗
dLS≤d≤dx为衍射传播距离,单位:km.
不规则地形中的衍射传播损耗通过结合基于菲涅耳-基尔霍夫理论的双刃峰模型和适用于光滑地面的Vogler修正模型来计算。
k=f/f0,γe=γa(1-0.04665eNs/N1)
(4)
(5)
dLS=dLS1+dLS2,dL=dL1+dL2
(6)
hej为收发天线有效高度,单位:m.
Xae=(kγe2)-1/3,为地球有效曲率
(7)

(8)
Aed=Adiff(max(dLS,dL+1.38Xae))-
mdmax(dLS,dL+1.38Xae)
(9)
Adiff(s)=(1-w)Ak+wAr+Afo
(10)
Afo=min(15,glg(1+αkhg1hg2σh(dLS)))
(11)
式(10)根据参数w确定双刃峰衰落Ak和圆形地球衰落Ar在衰落计算中的比重。
式(11)为杂波干扰衰落。
2) 视距(LOS)传播损耗
dmin≤d≤dLS为视距传播距离,单位 km.在LOS内,以反射传播机制为主,采用双线地面反射模型计算。
定义d2=dLSA2=Aed+mdd2
(12)
如果Aed≥0,那么d0=min(1/2dL,4×10-5he1he2f),否则
d0=max(1/2dL,min(-Aed/md,dL-2))
(13)
d1=3/4d0+1/4dL
(14)
A0=ALos(d0),A1=ALos(d1)
(15)
式中ALos=(1-w)Ad+wAt根据参数w确定衍射之外的损耗和双线理论损耗的比重。
3) 前向散射传播损耗
dx≤d为散射传播距离,单位 km.计算过程为
d5=dL+Ds,d6=dL+2Ds
(16)
ms=(Ascat(d5)-Ascat(d6))/Ds
(17)
dx= max(dLS,Xaelg(kHs),
(18)
(Ascat(d5)-Aed-msd5)/(md-ms))
式中Ascat(s)=10lg(kHθ4)+F(θs,Ns)+H0
(19)
以上Longley-Rice模型的推导可参考文献[6]和[9]。
2.仿真分析
2.1 地形剖面数据的获取
应用Longley-Rice模型的点对点模式进行计算时,需要获取收发信机之间详细的地形剖面数据。在仿真过程中采用质量较高的航天飞机雷达地形测绘使命高程数据SRTM[10],分辨率为90 m.SRTM数据有多种存储格式,此处使用ASCII格式存储的数据,通过读取ASCII文件头获取存储高程文件的基本信息,如行列数目(Nr和Nc)、起始经纬度(Xo和Yo)以及数据元大小Scell等,然后计算目标位置点相对起始点的偏移量Δn就能得到该点的高程数据。如果该点不能与文件中的位置相对应,则使用内插值方法,根据若干相邻点的高程值求出此点的高程值。SRTM高程数据的抽取过程如下:
1) 将ASCII文件中除去基本信息的实际高程数据网格化,网格数目为Nr×Nc.网格的起始点坐标O(0,0),终点坐标E(Nr,Nc).根据收发点的经纬度确定收发点在网格中的坐标

2) 根据收发点的坐标计算采样点数N=max(|XT-XR|, |YT-YR|)和采样点间距Δd=90λ,单位为m,其中λ=(YT-YR)/(XT-XR).
3) 采样点满足直线方程:y=λx+YR-λXR,由此得到采样点的坐标为
(Xi,Yi)=(xi,[yi])=(xi,[λxi])i∈(0,1,2,3,…,N)
进而求得所有采样点的高程值,也就得到了收发点之间的地形剖面数据。
在实验过程中,选取发射点坐标T(115.9°,42.7°),接收点坐标R(117°,43.5°),采样点数N=1 321,Δd=111.3 m,收发点间距d=146.9 km.抽取后的地形剖面如图3所示。

图3 从SRTM抽取的地形剖面图
2.2 接收机高度描述
在Longley-Rice模型的点对点模式中,需要明确信号发射机的结构高度以及接收机的结构高度,此处也就是飞行器距离地面的垂直距离。仿真时,可以假设飞行器在飞行过程中,飞行的海拔高度在一段时间内变化不大。但飞行器接收机的结构高度却时刻在变化着。


图4 飞行器在不同位置时的接收机高度描述
2.3 仿真分析
在仿真计算中各工作参数设定为:电波工作频率f=1 500 MHz,全向天线,垂直极化。发射机天线高度hg1=100 m,飞行器飞行海拔高度hm=1 665 m,地面电导率σ=0.005,相对介电常数εr=15,地球表面折射率Ns=320N.发射机坐标为(E115.9°,N42.7°),飞行器接收机的坐标随飞行器以固定的飞行海拔高度向着坐标为(E117.0°,N43.5°)的点沿直线飞行而不断变化,该地区的气候类型为亚热带大陆性气候。
仿真结果如图5所示。左坐标轴表示地形高程值,单位m,其中最左端标“●”处为发射机所在地;右坐标轴表示电波传播衰减,单位dB;图上端带箭头的虚线表示飞行器的飞行轨迹。从图5中可以看到,在视距最远端点之前的传播衰减值缓慢增长,且曲线较为光滑,这是因为飞行器飞临视距最远端点之前一直处于发射机的视距范围内,可以认为是自由空间传播。在视距最远端点处,飞行器和发射机之间恰好有山峰阻挡,故而此处的传播衰减值发生陡变,从158 dB剧增为188 dB.此点后的电波传播就以绕射衍射为主。值得注意的是当飞行器飞临地形中最高的山峰时,即在多重衍射区处,电波传播衰减不但没有增加,反而有所减少。这种现象就是波在衍射区域遇到阻挡物被反射回来时会进一步加强原有波的强度。随着飞行器越飞越远进入散射区域后,传播衰减值呈缓慢增长的趋势,地形的变化已经不是影响电波传播的主要因素,因此,不会引起传播衰减太大的波动。

图5 点对点模式下的传播衰减仿真
从图5的仿真结果可以看出:在散射区域之前,电波的传播损耗随地形的高低起伏发生明显的变化,说明应用Longley-Rice模型的点对点模式可以较精确地预测电波传播衰减。
3. 结 论
本文在对比分析现有电波传播模型及不同计算模式的基础上,确定了应用Longley-Rice模型的点对点模式作为飞行器控制通信电波传播损耗的仿真模型;抽取了SRTM高程数据作为电波传播路径剖面数据。仿真结果显示:飞行器在山区上空飞行,且在进入散射区域前,地形的变化是影响其控制通信信号传播的主要因素,同时也证明了以Longley-Rice模型的点对点模式作为飞行器在复杂地形上空飞行时的控制通信电波传播模型的有效性。因此,在得到飞行器所经路线的地形剖面数据后,可采用Longley-Rice模型的点对点模式对无线通信进行更加精确的预测。
[1] AMBROSINI T. Okumura Propagation Modeling[R]. [S.l.]: Wireless Communication, 1999.
[2] 张延华, 段占云, 沈兰荪, 等. Okumura-Hata传播预测模型的可视化仿真研究[J]. 电波科学学报, 2001, 16(1): 89-92.
ZHANG Yanhua, DUAN Zhanyun, SHEN Lansun, et al. Okumura-Hata radio propagation models using visual simulation[J]. Chinese Journal of Radio Science, 2001, 16(1): 89-92. (in Chinese)
[3] 王祖良, 樊文生, 郑林华. 海面电波传播损耗模型研究与仿真[J]. 电波科学学报, 2008, 23(6): 1095-1099.
WANG Zuliang, FAN Wensheng, ZHENG Linhua. Study and simulation on sea-surface propagation prediction model [J]. Chinese Journal of Radio Science, 2008, 23(6): 1095-1099. (in Chinese)
[4] EGLI J J. Radio propagation above 40 Mc over irregular terrain[J]. Proceedings IRE, 1957, 45(10): 1383-1391.
[5] National Bureau of Standards. Transmission Loss Predictions for Tropospheric Communication Circuits[S], 1967.
[6] LONGLEY A G, RICE P L. Prediction of Tropospheric Radio Transmission Loss Over Irregular Terrain, a computer method-1968[R]. Boulder: Institute For Telecommunication Sciences Boulder Co, 1968.
[7] 王祖良, 彭 茜, 郑林华. 移动通信信道损耗模型研究及仿真分析[J]. 电波科学学报, 2009, 24(1): 111-114.
WANG Zuliang, PENG Qian, ZHENG Linhua. Research and simulation analysis on missile-borne mobile propagation loss model[J]. Chinese Journal of Radio Science, 2009, 24(1): 111-114. (in Chinese)
[8] 徐红艳, 尉明明, 冯玉珉. 海上移动通信预测模型的选择[J]. 北京交通大学学报, 2005, 29(2): 65-68.
XU Hongyan, WEI Mingming, FENG Yumin. Selecting prediction model for sea mobile communication[J]. Journal of Beijing Jiaotong University, 2005, 29(2): 65-68. (in Chinese)
[9] HUFFORD G. The ITS Irregular Terrain Model, version 1.2.2- The Algorithm[R/OL]. Colorado: National Telecommunications and Information Administration Institute for Telecommunication Sciences,2002[2011-06-07].http://flattop.its.bldrdoc.gov/itm/itm_alg.pdf.
[10]JARVIS A, REUTER H I, NELSON A, et al. Hole-filled seamless SRTM data V4[CP/OL]. International Center for Tropical Agriculture (CIAT), 2008[2009-07-08]. http://srtm.csi.cgiar.org.

