低信噪比下对称三角线性调频信号参数估计
冯志红 赖 涛 赵拥军
(解放军信息工程大学,河南 郑州 450002)
引 言
在低截获概率(LPI)雷达中,调频连续波雷达由于结构简单、体积小、容易实现、具有较高的距离和速度分辨率等优点,在军用导航、战场侦察、成像与测高计等领域得到越来越广泛的应用[1]。对称三角线性调频连续波(STLFMCW)信号是调频连续波雷达中最常用的信号形式,因其易实现大的时宽带宽积,也是众多LPI雷达首选的信号形式,当雷达综合多种LPI措施并采用极低功率发射这种信号进行侦察时,对非协作性的电子侦察方而言,即使能检测到信号的存在,但要实现低信噪比条件下信号的参数估计仍然存在较大的挑战和困难。因此,研究低信噪比下STLFMCW信号的参数估计对现代电子侦察具有重要的现实意义。目前,国内外已有不少文献提出了各种参数估计方法,但大多基于合作接收机和先验信息部分已知的假设,且不适用于低信噪比环境下信号的参数估计。文献[2]采用Wigner分布对STLFMCW信号进行了分析,但Wigner分布由于受交叉项的干扰,难以提取出正确的参数信息。针对这一问题,文献[3]提出了基于Choi-Williams分布的STLFMCW信号检测与参数提取,能够抑制交叉项的干扰,但时频聚集性下降,影响估计精度。文献[4]提出一种基于Wigner-Hough变换的STLFMCW信号特征提取算法,该算法需要依次估计每段线性调频(LFM)信号参数,计算量非常大。文献[5]和文献[6]提出了一种基于Radon-Ambiguity变换和分数阶Fourier变换的STLFMCW信号检测与参数估计方法,把2维搜索降低为1维搜索,降低了运算量,能在-5 dB时得到较好的估计结果。文献[7]提出一种分数阶Fourier变换与聚类分析相结合的STLFMCW信号检测与参数估计方法,在低信噪比条件下具有较好的检测效果,但分数阶阶数的搜索与聚类算法运算量大。文献[8]提出了基于循环谱的STLFMCW信号的参数估计方法,从循环频率-频率域去估计信号的带宽与周期,具有较高的精度,但运算复杂,需要信号具有多个周期。
提出一种基于多相滤波器组和高阶累积量的STLFMCW信号参数估计方法。其中,多相滤波器组可以实现信号在频域上的快速均匀划分,给出信号完整的时频描述。高阶累量本身具备良好的抑制高斯噪声的能力,特别适合低信噪比条件下信号的检测识别与参数估计,因此对每个子带信号进行三阶累积量的短时估计时,不但保留了信号的有用信息而且能够有效抑制高斯噪声。包络检波后将较好地反映信号在相应时频点上的能量信息。STLFMCW信号在时频图上表现为多个对称三角形,通过对时频图进行Radon变换并提取频率曲线可得到复合信号各项参数的估计。本文方法无需已知信号参数方面的任何先验知识,可以在信噪比大于-12 dB条件下获得较高的估计精度。
2. STLFMCW信号模型
STLFMCW信号的每个周期包括正、负调频斜率的两部分LFM信号,信号构成方式如图1所示,所以STLFMCW信号表达式为
0≤t≤tm
(1)
tm≤t≤2tm
(2)
式中:A为信号幅度;fc为载频; ΔF为调制带宽;T=2tm为调制周期;μ+=ΔF/tm和μ-=-(ΔF/tm)分别为信号的正、负调频斜率。

图1 STLFMCW复合信号结构
2.算法原理
电子侦察接收机截获到的信号可表示为
s(t)=u(t)+n(t)
(3)
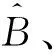

图2 参数估计流程
2.1 多相滤波器组与高阶累积量估计器设计
多相滤波器组相比于并联滤波器组具有结构简单,计算效率高等优点,其只需设计一个低通原型滤波器即可完成信号在频域上的快速划分,设低通原型滤波器的转移函数为
(4)
式中:h(n)为滤波器冲激响应;N为滤波器长度。则H(z)可以化为如下形式
(5)
式中:L为抽取比;
ρ=0,1,…,L-1
(6)
Q=[N/L],[·]表示取整,式(6)代表了H(z)的多相分量。令h(nL+ρ)=hρ(nL),第ρ路输入x(nL+ρ)=xρ(nL),则多相滤波器组的第ρ路输出为
tρ(nL)=xρ(nL)*hρ(nL)
(7)
对多相滤波器组的每组输出进行离散傅里叶逆变换(IDFT)运算,即可实现信号在频域上的均匀划分,其第i个输出频带的时域表达式为
(8)
式中:W=e-j2π/L; *表示共轭。因此,利用多相滤波器组能够实现信号在频域上的快速均匀划分。
高阶累积量包含常规简单低阶统计量所没有的相位信息,并且具备良好的抑制高斯噪声的能力,在低信噪比信号截获、检测中有着广泛的应用。信号经多相滤波器组分解为子带信号后,对每一个子带信号作三阶累积量的短时估计,以抑制高斯噪声。对一个零均值信号z(n),其三阶累积量短时估计为
zk(n+l1)zk(n+l2)
(9)
式中:S1=max{k-K,k-K-l1,k-K-l2};
S2=min{k+K,k+K-l1,k+K-l2};

w(n)为长度为2K+1的窗函数。K值的选取不能过大,否则会导致计算量过大并在输出中产生较大的误差;而若K值太小则不能有效抑制高斯噪声干扰,综合考虑本文选择K=2的布莱克曼窗。
k-K≤n≤k+K
(10)
信号经过正交滤波器后的第i个子带信号为
k-K≤n≤k+K
(11)
(12)
化简得
(13)
详细推导过程见文献[9],由式(13)可以看出,检测函数ρ3,i(k)不含任何的三阶谐波分量,因此可以有效减少各频带之间的混淆影响。对输出的每个子带信号进行三阶累积量对角切片短时估计后再进行包络检波,得到信号的时频矩阵|ρ3|为
(14)
式中:L为滤波器组数;Q为每组数据长度。利用时频矩阵|ρ3|可以得到信号的时频图。
仿真条件:信号带宽20 MHz,起始频率10 MHz,截止频率30 MHz,信号周期200 μs,设截获到2个完整的周期,采样频率fs=40 MHz.低通原型滤波器通带截止频率为0.625 MHz,阻带起始频率为0.65 MHz,阻带衰减为-80 dB,阶数为640,多相滤波器组数为64组,32倍抽取。在信噪比为-6 dB时包络检波后输出的时频图如图3所示,从图中可以看出,该时频图包含了我们需要估计的所有参数信息。图4为去噪后的信号时频图,对比可以发现高阶累积量能够很好地抑制高斯噪声,包含了我们需要估计的所有参数信息。
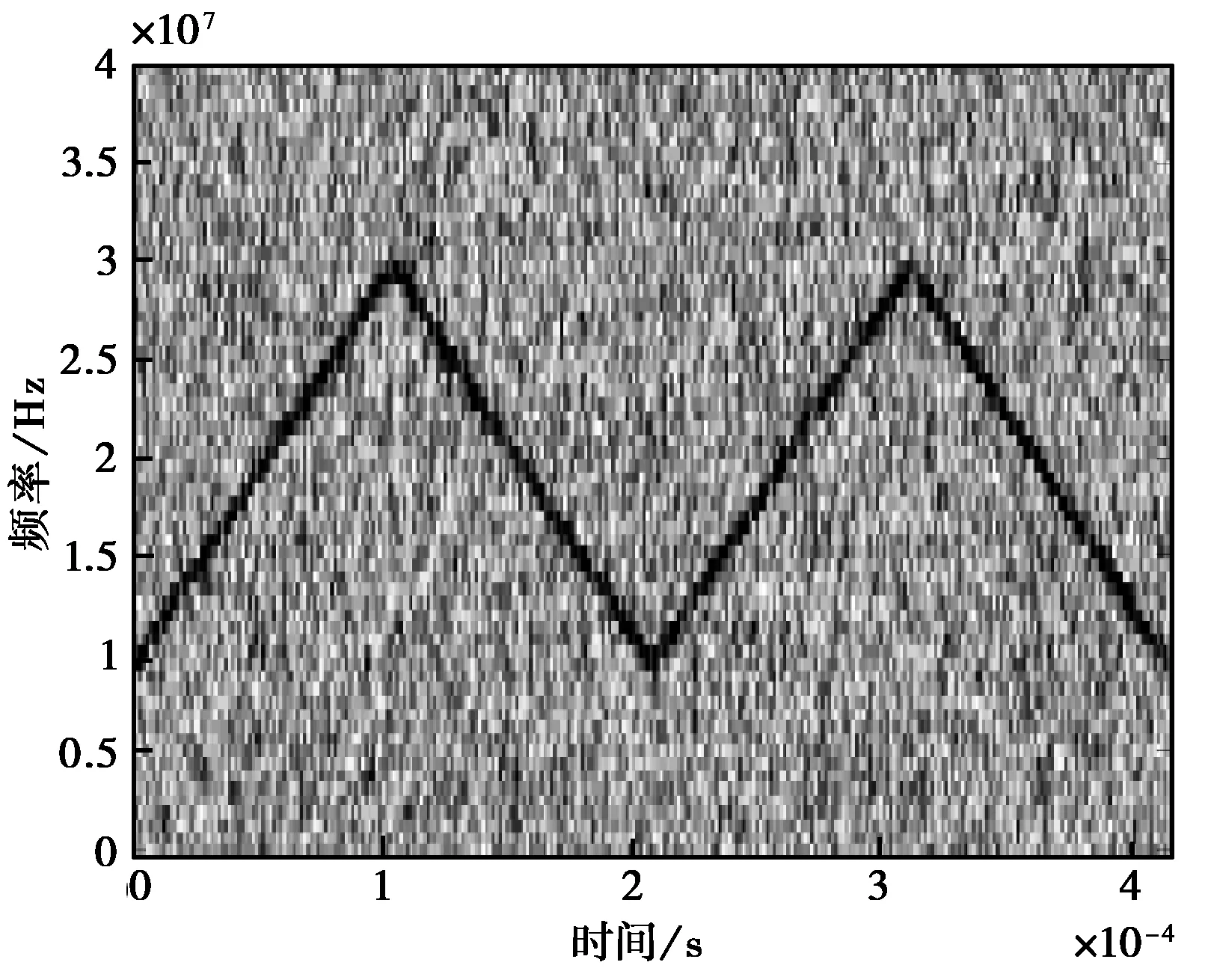
图3 STLFMCW信号时频图

图4 去噪后的STLFMCW信号时频图
2.2 基于时频图像的信号参数估计方法
由2.1节的分析可知,复合信号的时频图全面地反映了信号在时域和频域的参数信息,为提取图中信号的参数信息,对时频图进行Radon变换,Radon变换是图像处理中从图像中识别几何形状的基本方法之一。其基本原理是利用点与线的对偶性,将原始图像空间的给定的直线通过其表达式变为参数空间的一个点。这样就把原始图像中给定直线的检测问题转化为寻找参数空间中的峰值问题。设直线的参数方程为ρ=xcosθ+ysinθ,则一幅二维图像f(x,y)的Radon变换定义为

scosθ)ds
(15)

(16)

(17)

图5 R(ρ,θ)在θs角度处的一维切片
根据Radon变换原理,复合信号码元宽度T、带宽B与Radon变换后的θs、量平行直线间的距离d的关系如图6所示。

图6 复合信号时频图与Radon变换关系
根据图6所示的几何关系可知,调制周期的估计为
(18)
调频带宽的估计为
(19)
调频斜率的估计为
(20)
fs为信号的采样频率;L为滤波器组数。

图7 时频矩阵积分投影后得到的频率曲线
3.性能分析与仿真实验
3.1 计算量分析

3.2 仿真实验
为验证算法有效性,采用归一化均方根误差(NRMSE)作为衡量标准,设向量x=(x1,x2,…,xN)是x的N个估计值,则x的归一化均方根误差为.
(21)
采用与2.2节相同的仿真条件,仿真中采用零均值加性高斯白噪声,令信噪比从-15 dB到0 dB变化,每个信噪比下进行1 000次蒙特卡洛实验。仿真结果如图8和图9所示,图中分别给出了STLFMCW信号调频斜率、带宽、周期以及起止频率的估计结果。
图8给出了STLFMCW信号调制带宽、周期以及调频斜率的估计,从图中可以看出,在信噪比大于-12 dB时,本文提出的算法对STLFMCW信号参数估计误差较低,表明本文方法具有优良的抗噪声性能。图9所示为STLFMCW信号起止频率的估计,从图中可得,当信噪比大于-10 dB时,估计误差较小,验证了本文算法在低信噪比下的有效性。
图8 STLFMCW信号跳频频率估计的正确率

图9 STLFMCW信号其他参数估计的正确率
5.结 论
高阶累积量具有良好的抑制高斯噪声的能力,同时多相滤波器实现容易、运算效率高,不仅能够实现信号在频域上的快速划分,而且起到了改善信噪比的作用,所以本文将多相滤波器和高阶累积量结合起来,得到了STLFMCW信号完整的时频矩阵,实现了基于时频图像的信号参数估计,给出了STLFMCW信号的调频斜率、调制周期、带宽以及起止频率的估计方法。仿真结果表明本文方法估计正确率较高,抗噪性能较好,尤其是针对超大时宽带宽信号,本文方法在计算量上占有很大优势。但是本文方法也存在几个方面不足:其一,频率分辨率取决于多相滤波器组数,而增加滤波器组数会导致时间分辨率下降,实际中应根据需求权衡这两个参数;其二,起止频率估计精度与其所处的信道位置有关,若不是处于子信道中心最大值处,那么该频点信号会受到抑制,导致误差增大,不利于参数的提取。如何改善这两个方面的问题还需要进一步研究。
[1] PACE P E. Detecting and Classifying Low Probability of Intercept Radar[M]. Norwood: Artech House, 2009.
[2] GAU J Y. Analysis of Low Probability of Intercept Radar Signals using the winger Distribution[D]. Monterey: Naval Postgraduate School, 2002.
[3] UPPERMAN T L. Elint Signal Processing Using Choi-Williams Distribution on Reconfigurable Computers for Detection and Classification of LPI Emit-
ters[D]. Monterey: Naval Postgraduate School, 2008.
[4] LIU FENG, XU HUI FA, SUN DA PENG, et al. Feature extraction of symmetrical triangular LFMCW signal using Wigner-Hough transform[J]. Journal of Beijing Institute of Technology, 2009, 18(4): 478-483.
[5] 袁伟明, 王 敏, 吴顺君. 对称三角线性调频连续波信号的检测与参数估计[J]. 电波科学学报, 2005, 20(5): 594-597.
YUAN Weiming, WANG Min, WU Shunjun. Detection and parameter estimation of symmetrical triangular linear frequency modulation continuous wave signal[J]. Chinese Journal of Radio Science, 2005, 20(5): 594-597. (in Chinese)
[6] WAMG M, CHAN A K, CHUI C K. Linear frequency modulated signal detecting using ambiguity transform[J]. IEEE Transactions on Signal Processing, 1998, 46(5): 571-586.
[7] 刘 锋, 徐会法, 陶 然. 基于FRFT的对称三角LFMCW信号检测与参数估计[J]. 电子与信息学报, 2011, 33(8): 1864-1870.
LIU Feng, XU Huifa, TAO Ran. Detection and parameter estimation of symmetrical triangular LFMCW signal based on fractional Fourier transform[J]. Journal of Electronics & Information Technology, 2011, 33(8): 1864-1870. (in Chinese)
[8] LIMA A F J. Analysis of Low Probability of Intercept(LPI) Radar Signals Using Cyclostationary Processing[D]. Monterey: Naval Postgraduate School, 2002.
[9] SATTAR F, SALOMONSSON G. On detection using filter banks and higher order statistics[J].IEEE Transmon Aerospace and Electronic Systems, 2000, 36(4): 1179-1189.

