基于非齐次泊松过程的深空骨干节点流量分析
王小波 周贤伟 宋俊德
(1.北京科技大学计算机与通信工程学院通信工程系,北京 100083;2.北京邮电大学计算机学院,信息通信网络与服务工程中心,北京 100876)
引 言
深空通信网络或深空信息网络[1](DSINs)主要由行星际卫星及空间站组成,用以提供地球、外层空间行星及其子网、月球、卫星及中继站等信息传输的通用基础架构,包括在具有持久通信能力的元素间直接的与多跳路径的数据链路[2]。作为行星际网络的中继,深空骨干网络将各个行星子网联系起来称为一个整体,其承担着较大的数据通信量及各种服务请求,骨干网络节点的服务质量(QoS)提供能力将对整个深空通信网络的通信质量产生决定性的影响。
对深空骨干网络节点在一个时间段内接收到的服务请求数量及业务处理时间进行分析可以有效地估计各个节点上的数据通信及信息处理负担,从而对节点的QoS保证能力进行评价,为后续的路由提供参考,最大限度保障服务请求的QoS要求。然而现有的针对各类网络节点业务量的分析大都是假设服务请求业务按照齐次泊松过程到达,文献[3]提出的低轨卫星切换管理方法改善了切换阻塞率,但假设呼叫的持续时间服从负指数分布,即认为呼叫到达率为常数;文献[4]给出了一种自适应的信道分配算法,同样提高了呼叫阻塞率,不过也一样认为新的呼叫到达服从恒定参数的齐次泊松过程;文献[5]为低轨卫星的切换提出了一种新的队列策略,提高了呼叫的成功率并降低了阻塞率,但文中将呼叫建模为M/M/S队列系统,同样认为呼叫到达率λ是常数。在以上文献及类似研究中,都将呼叫或服务请求到达率假设为常数,通过齐次泊松过程对过程建模,然而这与实际情况并不符合,因为服务请求数量在某个时间段内应该是随时间变化的,在深空通信网络间断连接的条件下更是如此。
本文假设服务请求到达率是随时间变化的函数λ(t)可以更贴近实际情况,通过计算用户所关注时间段内的节点业务到达数量和时间间隔概率密度,不但可以较为直观地估计深空骨干网节点的QoS提供能力,同时可以为地球卫星通信中呼叫接入控制及切换提供更切实的理论依据,并为路由节点选择提供一定的参考。
1. 深空通信网络结构及网络业务流量模型
1.1 深空通信网络结构
基于美国国家航空航天局(NASA)的行星间因特网(IPN Internet),深空通信网络基本结构如图1所示。
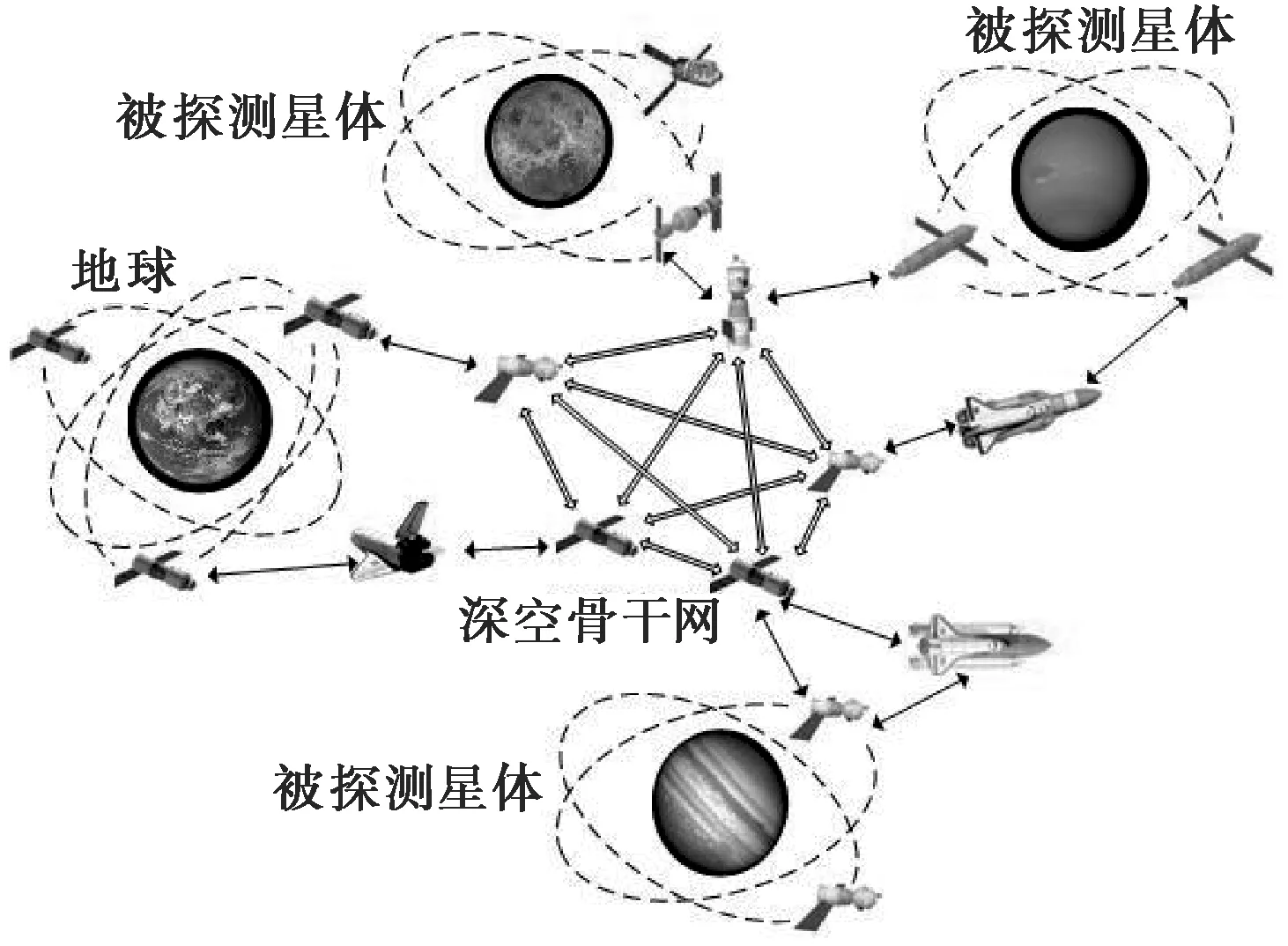
图1 深空通信网络结构图
深空通信网络基础架构的基本组成部分有[6]:①深空骨干网络,主要部署在各个被探测星体之间作为各星体间通信的中继网络,提供遥远星体或航天器之间的多跳可靠连接;②行星外层网络,主要由各行星的卫星网络或航天器组成,用以提供对行星表面的通信覆盖以及与深空骨干网络的有效连接;③行星表面网络,由行星表面的探测器及近地飞行器组成,用以在行星表面提供可靠的无线通信,并且可与行星外层网络直接或间接通信,进行数据传输。
深空骨干网络作为整个深空信息网的中转站,承担了大量的数据转发任务,对其节点的QoS提供能力进行分析具有重大意义。
1.2 传统网络业务流量模型
网络业务流量特征分析是进行高性能通信协议设计、负载均衡、提供QoS保障的基础,同时也可对路由选择提供依据,深空环境也是如此。合适的网络业务流量模型可以帮助人们针对特定网络环境设计更好的协议、采取更有效的QoS保证手段、保证关键业务得到必要的QoS.传统的网络业务流量模型一般是基于泊松过程的,比较经典的主要有以下几种[7-8]。
1) 泊松(poisson)模型
泊松模型最早是基于电话业务特征而提出的,可以较为准确地描述电话网中的业务流量特征从而得到广泛应用。在早期的网络业务流量建模中,泊松模型被广泛使用。泊松模型是指对任何t,s≥0,N(s,t+s]服从参数为λt的泊松分布,即
(1)
从而可以计算出其相应的业务到达时间间隔序列呈负指数分布。泊松过程的强度λ表示单位时间间隔内业务量出现的期望值,λ越大,单位时间内平均出现的业务量越多,这正是λ称为泊松过程强度的原因。
2) 马尔可夫(Markov)模型
马尔可夫模型是一种基于Poisson过程建模的模型,建立的基础是无后效性和平稳性。无后效性意味着下一个状态仅仅依赖于当前状态,而与过去的状态无关,考虑的只是相邻两个状态之间的相关性。平稳性是指在较长时间后马尔可夫过程趋于稳定状态,而与初始状态无关。如果把“时刻n”看做“现在”,马尔可夫性可以解释为“知道现在”, “过去”与“将来”是相互独立的,即如果在已知随机事件An发生的条件下,An+1,An+2,…,中的某些事件的发生,与A1,A2,…,An-1中的事件的发生与否无关,则称这一串事件{An∶n≥1}具有马尔可夫性。常见的马尔可夫模型主要有以下几种:开-关源模型(On-Off 模型),中断泊松过程模型,状态交替更新过程,马尔可夫调制泊松过程,马尔可夫调制流过程。
3) 回归(regression)模型
回归模型随机序列中,下一时刻随机变量值是由当前和过去若干个随机变量值以及一个白噪声的函数来决定的。常见的回归模型有:自回归模型(AR),离散自回归模型(DAR),自回归滑动平均模型(ARMA),求和自回归滑动平均模型(ARMA),变换扩展采样模型(TES)。其中自回归模型、离散回归模型、自回归移动平均模型要求流量序列是平稳序列,而自回归移动平均求和模型可以处理有周期性和趋势性的非平稳序列,变换扩展采样模型则适合用来描述高速突发业务流。
以上传统的业务流量模型优点是概率理论及相关知识体系发展比较完善,队列系统性能评价容易得到解析结果。然而,以泊松过程理论为基础的传统模型,大多存在一定缺陷,尤其是深空这种业务量在时间和空间上服从一定规律性的特定环境中。例如,实际业务量到达是相关联的且并不严格服从泊松分布时,过程强度函数通常不为常数,而是随时间呈现某种规律。在文献[9]中,分析了卫星网络的流量负载随时间变化情况,发现上传和下载流量均随时间呈现某种规律性变化,说明服务请求数量也呈现相应变化规律。深空通信中节点的流量特性还取决于地面通信需求量,由于地球上的地域差别、不同区域的人口密度差异,不同区域的通信需求量也不尽相同,在文献[10-11]中,就分析了地面系统流量非均匀分布所带来的影响。因此,需要采用非齐次泊松过程对深空通信中骨干节点业务量进行描述和建模,并结合马尔可夫序列理论进行分析,假设过程强度不为常数且呈现某种规律性,以期更为贴近实际情况。
2. 深空骨干网节点业务流量分布模型
由于深空网络具有长传播延时、高误码率等特点,因此对于节点的业务到达数量及时间间隔分布进行估算具有十分重要的意义,同时可为后续的深空节点流量负载均衡提供参考。而在节点QoS能力评价方面,通常采用节点可用时长、链路质量来进行衡量[12],以流量均衡为目标的路由选择及决策可以避免拥塞、降低链路时延,对于提高链路QoS指标具有显著效果[13-14]。为简便起见,这里将节点业务看作一定数量的服务请求,节点对到达业务的处理即为对服务请求的响应。由于假设业务的服务请求到达率不为常数,因此在某个时间段内的业务到达数量也就不再服从泊松分布,相应的情况将变得更加复杂。下面从一类特殊非齐次泊松过程—带时倚强度泊松过程的定义入手,得出相关结论。
定义1[15]计数过程{Nt;t≥0}称为带时倚强度的泊松过程,如果它满足下列条件:
①P(N0=0)=1
② 对任意t≥0和h>0,当h→0时:
P1[t,t+h)=P(Nt,t+h=1)=λ(t)h+o(h)
③ 在互不相交区间上增量具有独立性
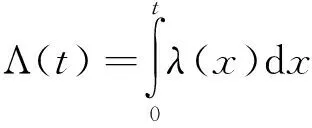

P(Nt,t+s=n) =exp{-[Λ(t+s)-Λ(t)]}×
[Λ(t+s)-Λ(t)]n/n!
(2)
类似于假设服务请求到达分布服从齐次泊松过程的情形,也能推导出带时倚强度泊松过程的到达时间和到达时间间隔的一些有关的分布。对于齐次泊松过程,当给定过程在(0,L]时间段内有n个服务请求到达时,这n个服务请求到达时间S1,…,Sn的条件联合分布和n个在(0,L]上均匀分布的独立随机变量的次序统计量的分布相同。利用类似的推理可以把此结果推广到时倚强度的情形。
定理1:设{Nt,t≥0}是带时倚强度λ(t)的泊松过程。对于任意正整数n,过程的前n个到达时间S1,…,Sn的联合分布密度函数为
fS1,…,Sn(t1,…,tn)
(3)
证明:
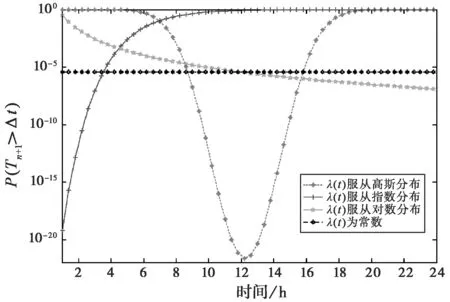
P(ti-Δti =P(N0,t1-Δt1=0; Nti,ti+1-Δti+1=0,1≤i≤n-1; Nti-Δti,ti=1,1≤i≤n) 根据联合发生密度的定义有 fS1,…,Sn(t1,…,tn) 类似的,过程的任意n个到达时间的联合分布密度函数可由定理2给出。 fSr+1,…,Sr+n(tr+1,…,tr+n) (4) 带时倚强度λ(t)的泊松过程{Nt,t≥0}的到达时间序列S1,…,Sn,…是一马尔可夫序列,按转移密度的定义和过程的n个发生时间的联合分布密度函数可知它的转移密度为 PSn|Sn-1,…,S1(tn|tn-1,…,t1) (5) 而 (6) 可见式(5)和式(6)表达式一致。已知具有常数强度λ的齐次泊松过程的到达时间间距Tn=Sn-Sn-1(n=1,2,…)相互独立而且都有参数为λ的指数分布。当强度不再是常数而是随时间变化时,Tn一般就既不是相互独立,也不再有相同分布了。但是,由过程的无后效性易知当给定了S1,…,Sn时,第n+1个到达时间间距Tn+1=Sn+1-Sn是独立于S1,…,Sn-1的。因此,由以上结果可以推出给定S1,…,Sn时Tn+1的条件密度函数为 fTn+1|Sn,…,S1(t|Sn,…,S1) =fSn+1|Sn,…,S1(Sn+t|Sn,…,S1) [10]Oxford,R.L.Language Learning Strategies:What Every Teacher Should Know.New York:Newbury House.1990. =fSn+1|Sn(Sn+t|Sn) (7) 由式(7)得到条件分布函数为 P(Tn+1≤t|Sn=sn,…,S1=s1) (8) 由式(2)可知,在时长h的时间段内到达的服务请求数量小于k的概率为 P(Tt+h-Nt (9) 从以上分析可知,在已知服务请求到达率函数λ(t)的情况下,由式(8)可以对节点到达服务请求时间间隔小于某个限定值的概率进行估算,得出其概率取值范围。而由式(9)可以得到在某个时间段内服务请求到达数量小于某个阈值的概率。在此基础上可以对深空骨干网节点业务量进行初步的估计,从而为后继的路由节点选择及负载均衡提供依据。 为了更加直观地展现前文提出的深空通信网络骨干节点所收到的业务流量分布特点,我们进行了进一步的数值分析。为了估计服务请求在未来的某一时间段Δt内得到成功响应的可能性,需要计算下一次请求到达时间间距大于Δt的概率。由于请求的服务时间决定于节点所收到的请求数,为了保证系统中的服务请求得到充分响应,必须保证系统中的请求数小于某一值的概率。 我们分别比较了服务请求到达率符合高斯分布函数、指数分布函数、对数函数,以及通常采用的服务请求到达率为常数时Δt时间段内无服务请求到达的概率P(Tn+1>Δt),以及在时长h的时间段内到达的服务请求数量小于k的概率P(Nt+h-Nt 表1 服务请求到达率函数 在图2中仿真时间为24 h,Δt=0.5,即半小时内无服务请求到达的概率。用表1所示的函数模拟了不同的服务请求到达率,在实际中也可以根据实测统计数据采用相应函数进行拟合。 图2 Δt时间段内无服务请求到达的概率 随时间变化趋势 由图1可以发现,P(Tn+1>Δt)与到达率函数变化趋势相反,即当服务请求到达率增加时,未来Δt内无请求到达的概率变小。图3显示了间隔时长h在不同时刻对到达的服务请求数量小于k(k=5)的概率的影响,可以看出,随着h的增大,概率基本呈现减小的趋势,且函数变化趋势越明显则减少越剧烈,这意味着间隔时长越长出现更多服务请求的概率越大。图4展示的是数量k对请求数量小于k的概率在不同时刻的影响,Δt=0.5,k与概率值变化趋势基本一致,而在k一定时,如果λ(t)是增函数,意味着单位时间内到达的服务请求将增加,从而导致Δt内服务请求数量小于k的概率减小,相反,则概率增大。 由以上分析可见,相对于传统的假设服务请求到达率为常数的情况,新的方法更具有广泛性,能适应各种不同条件下的服务请求到达分布,更接近实际情况,对于由地域因素及卫星等深空节点规律性运动所引起的服务请求到达率变化可以进行较好的数值拟合。同时,为深空节点存储转发策略与路由节点选择也能提供更可靠的依据。 深空通信网络环境复杂,具有长时延、传输距离远等特点。对骨干节点的业务量特点进行分析可以明确节点的QoS提供能力,从而充分利用整网资源,避免单个节点负载过重,降低业务的排队等待时间。在假设服务请求到达率不为常数的情况下,某个时间段内的服务请求到达率可以由经验数据分析得到,采用相应函数拟合,从而在所关注的时间段内更贴近实际情况来分析节点负载。 文中提供了一个对深空骨干网节点业务量估计的较为直观的参考,其方法为深空通信网络节点负载分析提供了一种新的研究思路,为深空通信网络路由节点选择提供了一定的依据。当然,深空通信网络的研究仍然处于初期,还有更多的问题等待我们去解决,文中的方法及思路也还有待探讨完善。 [1] ZHOU Xianwei, ZHANG Long, CHENG Zhimi, et al. Hypernetwork model and architecture for deep space information networks[C]//Proceedings of the 2010 IEEE International Conference on Future Information Technology(ICFIT’10). Changsha, China, Dec 14-15, 2010: 448-452. [2] 周贤伟. 深空通信[M]. 北京: 国防工业出版社, 2009: 222. [3] CHO S, AKYILDIZ I F, BENDER M D, et al. A new spotbeam handover management technique for leo satellite networks[C]// IEEE Global Telecommunications Conference. San Francisco, CA, USA, 2000: 1156-1160. [4] CHO S. Adaptive dynamic channel allocation scheme for spotbeam handover in LEO satellite networks[C]//IEEE Vehicular Technology Conference. Boston, MA, USA, 2000: 1925-1929. [5] KIAMOUCHE W, BENSLAMA M. Pseudo last useful instant queuing strategy for handovers in low earth orbit mobile satellite networks[J]. International Journal of Information Technology, 2008, 4(5): 369-375. [6] AKYILDIZ I F, AKAN O B, CHEN C, et al. InterPlaNetary internet: state-of-the-art and research challenges [J]. Computer Networks Journal, Elsevier Science, 2003, 43(2): 75-112. [7] 张 宾, 杨家海, 吴建平. Internet流量模型分析与评述[J]. 软件学报, 2011, 22(1): 115-131. ZHANG Bin, YANG Jiahai, WU Jianping. Survey and analysis on the internet traffic model [J]. Journal of Software, 2011, 22(1): 115-131. (in Chinese) [8] 周晓玮. 网络流量的模型分析和异常检测[D]. 大连: 大连海事大学, 2006. ZHOU Xaiowei. The model analysis and anomaly detection of network traffic[D]. Dalian: Dalian Maritime University, 2006. (in Chinese) [9] SHAO Q. Measurement and analysis of traffic in hybrid satellite-terrestrial network [D]. Burnaby: Simon Fraser University, 2004. [10] SATO S. A performance analysis on nonuniform traffic in micro cell systems[C]// Proc. IEEE ICC’93. Geneva, Switzerland, May 23-26, 1993(3):1960-1964. [11] TALEB T , JAMALIPOUR A , KATO N. IP traffic load distribution in NGEO broadband satellite networks[J]. Computer and Information Sciences, 2005, 3733: 113-123. [12] HADJITHEODOSIOU M H, NGUYEN A T. Using commercial satellites to provide communication support for space missions[C]// IEEE Global Telecommunications Conference. San Francisco, CA, USA, 2000, 2:1135-1139. [13] YAO Danlin, WANG Cheng, SHEN Jianhui. Traffic-adaptive hybrid routing algorithm for double-layered satellite networks[C]// Biomedical Engineering and Informatics. Tianjin, China, October, 17-19, 2009: 1-6. [14] YUAN Zhe, ZHANG Jun, LIU Zhongkan. Routing in LEO/MEO double-layered satellite networks[C]// International Conference on Wireless Communications, Networking and Mobile Computing, September,22-24, 2006: 1-4. [15] 邓永录, 梁之舜. 随机点过程及其应用[M]. 北京: 科学出版社, 1992: 61-71.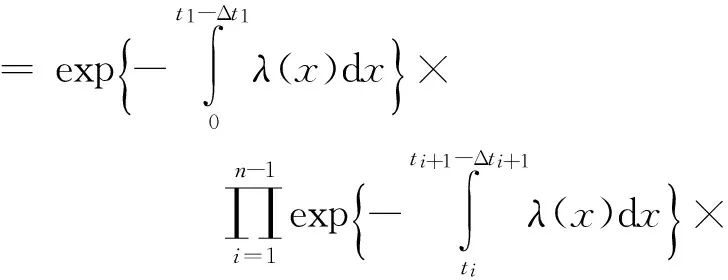
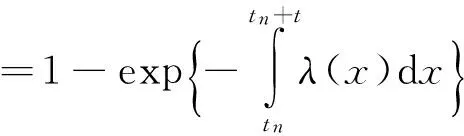
3.仿真结果与分析

4. 总结与展望

