三维空间中近距离多天线信道的容量分析
吴 睿,张祖凡
(1.成都工业学院 电子工程学院,四川 成都 611730;2.重庆邮电大学 通信与信息工程学院,重庆 400065)

三维空间中近距离多天线信道的容量分析
吴 睿1,张祖凡2
(1.成都工业学院 电子工程学院,四川 成都 611730;2.重庆邮电大学 通信与信息工程学院,重庆 400065)
针对多天线系统在近距离和远距离2种场景下信道矩阵的差异,基于球面波模型进行信道容量分析,并通过使用球面波模型(spherical wave model,SWM),研究了三维空间中近距离多天线直线传播(line of sight,LOS)信道容量。相比现有基于信道测试和计算机仿真的研究方法,在三维空间中建模任意方向的线性天线阵列,给出球面波模型下的近距离LOS信道矩阵,在此基础上推导了近距离LOS信道容量的闭式解。通过信道容量的闭式解和计算机仿真分析了影响近距离LOS信道容量的参数,揭示了近距离LOS信道容量的本质特征。理论和分析结果表明,在三发三收近距离LOS信道中,信道容量是“类余弦”的函数,即具有类似余弦函数的周期振荡特性,其变化特征由波长、阵元间隔、收发通信距离和阵列方向完全决定,通过合理设计这些参数使近距离LOS信道容量达到最大。
信道容量;LOS信道;球面波模型(SWM);近距离通信
0 引 言
新一代移动通信系统对低功耗、泛在接入、极高频谱效率的迫切需求,使得近距离多天线通信场景所占比例越来越大。在远距离多天线通信中,收发通信距离通常远远大于100倍波长,能近似用平面波模型建模直线传播(line of sight,LOS)信号,相应的信道矩阵通常不满秩,因而信道容量将急剧下降[1]。然而,在含有LOS信号的近距多天线通信中,收发通信距离与阵列尺寸是相比拟的,如果继续使用平面波模型,那么信道容量将会被低估[2],因此,球面波模型比平面波模型更适合在近距离通信中。

上述文献[2]和文献[3]都是基于信道测试和计算机仿真来研究近距离多天线LOS信道容量,未见深入的理论解析分析,所以,并没有分析出近距离多天线LOS信道容量的本质特征。文献[4-6]本质上研究的是近距离多天线LOS信道的最大容量,但没有给出信道容量的闭式解。文献[7]主要研究近距离多天线LOS信道的空间复用能力,文献[8]研究的是信道容量的统计特性,它们都没有分析哪些关键参数影响信道容量。
本文用球面波建模了三发三收的近距离多天线LOS信道,推导出信道容量的闭式解,描述了信道容量的本质特征,给出决定信道容量的关键参数。研究结果显示,三发三收近距离LOS信道容量完全由波长、阵元间隔、收发通信距离和阵列方向所决定,并且信道容量随着这些参数剧烈的波动。同时,推导出了使近距离三发三收LOS信道容量达到最大的准则,该准则可以直接运用到近距离通信场景中。
1 天线架构
三发三收近距离均匀线性天线阵列的布局如图1所示。由于空间中任意3个点能决定1个平面,不失一般性,可以假设发射天线阵列与接收天线阵列中的第1个天线单元Rx1位于xoy平面,发射天线Tx1和接收天线Rx1所在直线Tx1—Rx1为y轴,原点位于Tx1。在图1中,θt和θr分别表示发射阵列和接收阵列的方向角;φr表示接收天线的高度角;dt和dr分别表示发射天线阵列和接收天线阵列的阵元间隔;R表示Tx1与Rx1之间的距离即收发通信距离。
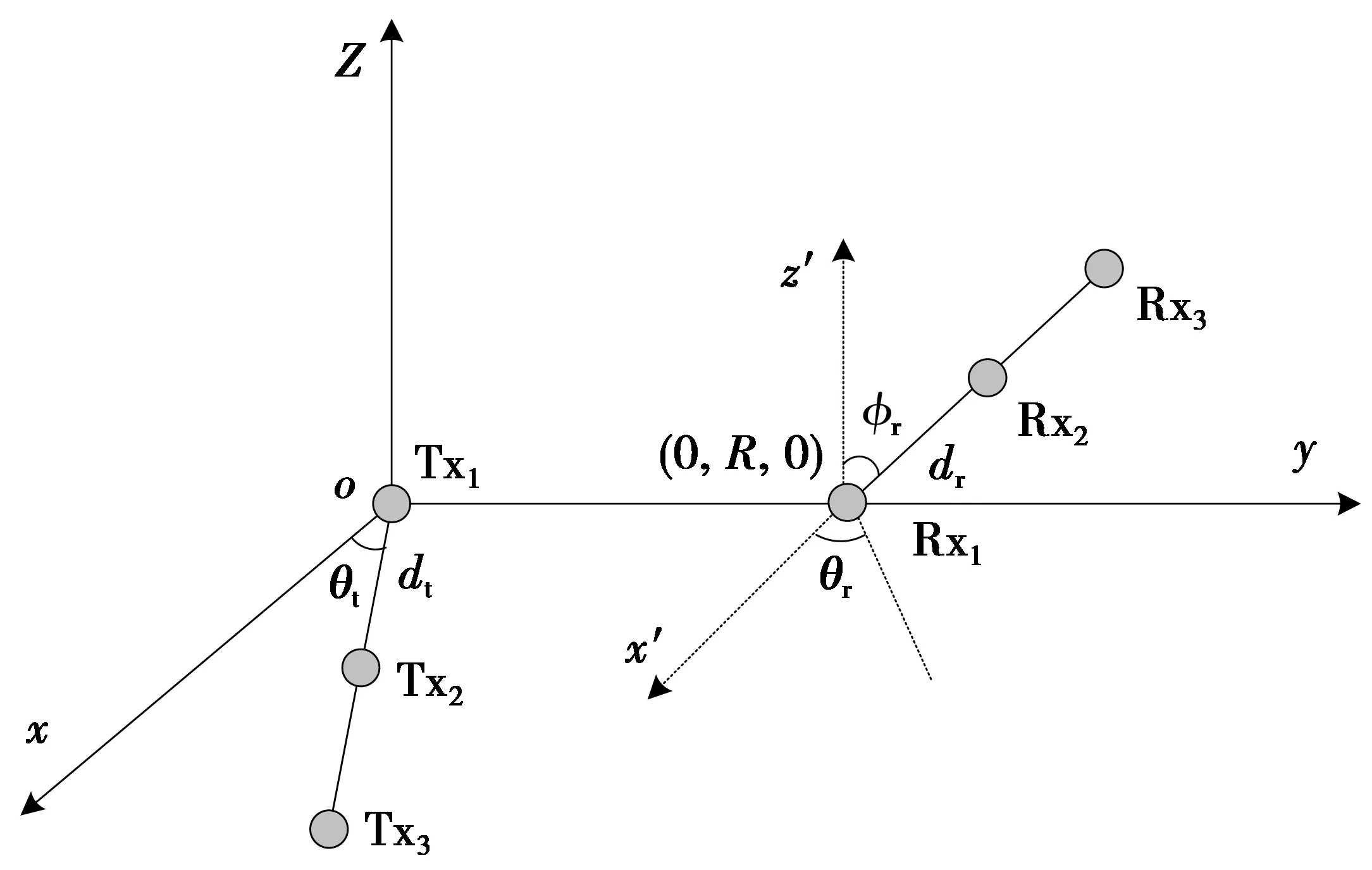
图1 三发三收均匀线阵天线配置示意Fig.1 Setup of 3×3 transmit and receive uniform linear array antennas
2 近距离多天线LOS信道容量的闭式解
这里考虑球面波模型下LOS信道,LOS信道矩阵的元素可以表示为[1]
(1)
(1)式中:hn,m表示第m(m=1,2,3)个发射天线与第n(n=1,2,3)个接收天线之间的冲击响应;λ表示波长;G表示发射和接收天线场辐射模式在LOS方向的乘积;dn,m表示第m个发射天线与第n个接收天线之间的距离。假设路径损耗差能忽略[9-10],从而三发三收多输入多输出(multiple-input-multiple-output,MIMO)系统的归一化LOS信道矩阵为
(2)
根据图1中的天线配置,并使用文献[9]和文献[10]的分析方法,距离dn,m为
(3)
(3)式是通过泰勒级数展开,并取其第一阶项,让分母近似等于2R而得到[9-10];这对实际的无线系统来说,该近似所引入的误差非常小[10]。
根据(2)-(3)式,矩阵HHH为
(4)
(4)式中:a,b,c和Γ分别为
(5)
进一步,(4)式中矩阵HHH的特征值为
(6)
当发射端未知信道状态信息(channel state information,CSI)时,发射功率应该均等地分配在所有发射天线上,从而发射端未知CSI的信道容量为[11]
(7)
(7)式中:γ表示每个接收天线的平均信噪比(signal to noise ratio,SNR)。将(6)式代入(7)式中,在使用球面波模型下三发三收近距离LOS信道的容量为
(8)
(8)式中,Γ=(2πdtdrcosθtsinφrcosθr)/(Rλ)。从(8)式可知,近距离多天线LOS信道的容量是“类余弦”函数,即具有类似余弦函数的周期振荡特性,其他振荡变化特征完全由波长、阵元间隔、收发通信距离和阵列方向所决定,并且随着这些参数而波动。
从(6)式中的特征值可知
(9)
(9)式成立,即,
(10)
(10)式成立时(k∈Z,Z表示整数集合),特征值ξ1=ξ2=ξ3=3,相应(8)式中的信道容量达到最大值,即
Cmax=lb(1+3γ+3γ2+γ3)
(11)
可以将准则(10)式直接运用到近距离三发三收的通信场景中,使其信道容量达到最大。当Γ=2kπ时,特征值ξ2=9和ξ1=ξ3=0,相应的信道容量达到最小值,即
Cmin=lb(1+3γ)
(12)
从而,随着参数Γ,球面波模型下三发三收的近距离LOS信道容量在最小值与最大值之间波动,并且通过合理的设计参数Γ,在近距离LOS信道中能达到最大的容量。
另一方面,根据文献[4]的研究结果,平面波模型下的三发三收近距离LOS信道的容量始终为
C=lb(1+3γ)
(13)
对比(8)式和(13)式可知,平面模型下的信道容量与球面波模型下的信道容量的最小值相同,并且平面波模型不能反映近距离LOS信道容量的本质特征,会低估近距离LOS信道的容量。
3 数值与仿真结果
为了验证上面理论分析结果的正确性,给出了计算机仿真结果。仿真分析是通过使用MATLAB软件首先计算出球面波模型下的信道矩阵,然后对信道矩阵进行奇异值分解算出特征值,最后算出信道容量。
图2给出了使用球面波模型下三发三收近距离LOS信道容量与高度角之间的关系,其中,方向角θt=θr=0°,收发通信距离R=5 m,信噪比为20 dB,收发阵列间隔dr=dt=0.18 m。从图2中可以观察到,理论分析结果和数值仿真分析十分吻合,并且球面波模型下的近距离LOS信道容量随着高度角变化而变化。从图2中还可以看出,在频率为73 GHz,20 GHz和2 GHz时,最大的信道容量分别为19.27 bit/(s·Hz),19.27 bit/(s·Hz)和11.62 bit/(s·Hz),最小的信道容量为8.23 bit/(s·Hz);因此,可以通过合理设计阵列的高度角,得到更高的近距离LOS信道容量。

图2 不同频率下三发三收近距离LOS信道容量与高度角的关系Fig.2 Capacity of 3×3 short-range LOS Channel for different elevation angle
根据近距离LOS信道容量闭式解(8)式可知,近距离LOS信道容量除了会随着高度角波动外,还会随着波长、阵元间隔、收发通信距离和方向角而剧烈的波动。再根据上面理论分析可知,可以通过设计这些参数让(10)式成立,相应的近距离LOS信道容量能达到最大值。
图3给出球面波模型下三发三收近距离LOS信道容量与参数Γ之间的关系,其中,信噪比分别为10 dB和20 dB。从图3中可以观察到,理论结果和仿真分析十分吻合,从而证明了理论分析的正确性;并且信道容量随着参数Γ变化而变化。当信噪比为20 dB时,最大信道容量和最小信道容量分别为19.27 bit/(s·Hz)和8.23 bit/(s·Hz);当信噪比为10 dB时,最大信道容量和最小信道容量分别为10.38 bit/(s·Hz)和4.95 bit/(s·Hz)。同时,信道容量在最大值和最小值之间进行周期性的波动。
4 总 结
本文使用球面波模型,研究了三维空间中近距离多天线LOS信道容量。通过推导的信道容量的闭式解,分析影响信道容量的关键参数,揭示了近距离多天线LOS信道容量的本质特征。研究结果显示,近距离多天线LOS信道容量完全由波长、阵元间隔、收发通信距离和阵列方向决定,并且随着这些参数剧烈的波动,可以通过合理的设计这些参数使近距离多天线LOS信道容量达到最大。

图3 不同信噪比下三发三收近距离信道容量与参数Γ之间的关系Fig.3 Capacity of 3×3 short-range LOS Channel for different
[1] TSE D, VISWANATH P. Fundamentals of Wireless Communication. Cambridge [M]. U.K.: Cambridge Univ Press, 2005.
[2] JIANG J S, INGRAM M A. Spherical wave model for short-range MIMO [J]. IEEE Trans Commun, 2005, 53(9): 1534-1541.
[3] SKENTOS N, KANATAS A G, PANTOS G, et al. Capacity results from short range fixed MIMO measurements at 5.2 GHz in urban propagation environment [C]∥IEEE ICC. Paris, France: IEEE, 2004: 3020-3024.
[4] BØHAGEN F, ORTEN P, ØIEN G E. On spherical vs. plane wave modeling of line-of-sight MIMO channels [J]. IEEE Trans Commun, 2009, 57(3): 841-849.
[5] GILL S, PETERSEN B. Line-of-sight multi-input multi-output capacity improvement using change of carrier frequency[C]∥International Conference on Advances in Computing, Communications and Informatics (ICACCI). Mysore, India: IEEE, 2013: 321-326.
[6] XUMIN Pu. Optimal 2×2 Antenna Placement for Short-Range Communications[J]. IEEE Communications Letters, 2013, 17(08): 1560-1563.
[7] XUMIN Pu. Effects of Array Orientations on Degrees of Freedom for 3D LoS Channels in Short-Range Communications[J]. IEEE Wireless Communications Letters, 2015, 4(01): 106-109.
[8] XUMIN Pu. Analysis of the Capacity Statistics for 2×2 3D MIMO Channels in Short-Range Communications[J]. IEEE Communications Letters, 2015, 19(02): 219-222.
[9] BØHAGEN F, ORTEN P, ØIEN G. Design of optimal high-rank line-of-sight MIMO channels [J]. IEEE Trans Wireless Commu, 2007, 6(4): 1420-1425.
[10] SARRIS I, NIX A R. Design and performance assessment of high-capacity MIMO architectures in the presence of a line-of-sight component [J]. IEEE Trans Veh Technol, 2007, 56(4): 2194-2202.
[11] PAULRAJ A, NABAR R, GORE D. Introduction to Space-Time Wireless Communications[M]. U.K: Cambridge Univ Press, 2003.

吴 睿(1981-),女,四川乐山人,讲师,硕士,主要研究领域为通信与信息系统,信号与信息处理,电子测量等。E-mail: 359621366@qq.com。

张祖凡(1972-),男,湖北石首人,教授,博士,主要研究领域为无线通信理论与技术。E-mail: zhangzf@cqupt.edu.cn。
(编辑:刘 勇)
Analysis of the capacity for short-range multi-antenna channels in 3D space
WU Rui1, ZHANG Zufan2
(1. School of Electronic Engineering, Chengdu Technological University,Chengdu 611730,P.R. China; 2. School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China)
Short-range multi-antenna line-of-sight (LOS) scenarios occurs more frequently than long-range multi-antenna LOS cases. However, plane-wave model is not suitable for short-range LOS cases. Unlike previous study based on channel sounding and simulation, we investigate the capacity for short-range multi-antenna LOS channels with the spherical-wave model (SWM) in three-dimensional (3D) space to obtain its close-form. The antenna array with arbitrary orientations in 3D space is modeled, and the channel matrix with the SWM is then derived. Based on this obtained channel matrix, the exact closed-form expression for the channel capacity is derived without channel state information (CSI) at the transmitter. By using the closed-form expression for the capacity and computational results, we analyze the factors governing the capacity behavior, and give the essential characteristics of the capacity for short-range LOS channels with the SWM. Both the analytical and computational results show that the capacity for short-range LOS channels with three transmitting and three receiving antennas reflects the cosine behavior, and the capacity is determined by the wavelength, the inter-element spacings, the transceiver distance and the orientations of the arrays. And the capacity can be maximized by specifically designing these parameters.
channel capacity; line-of-sight(LOS) channels; spherical-wave model(SWM), short-range communications
10.3979/j.issn.1673-825X.2016.06.012
2015-11-05
2016-06-02
吴 睿 359621366@qq.com
港澳台科技合作专项学课题(2015DFT10170)
Foundation Item:The Science and Technology Cooperation Projects for Hong Kong, Macao and Taiwan areas(2015DFT10170)
TN915
A
1673-825X(2016)06-0822-05

