基于网页浏览行为的分析
米 雪, 张 宁
(上海理工大学管理学院,上海 200093)
探索人类各种行为的统计特性,是探索自然界、认知人类自身的一个重要方面,对于研究经济、心理和众多社会学科有着重要的意义.在研究涉及人类行为特性的问题时,一个常常采用的传统近似是,将人类的行为简化为可以使用泊松过程描述的稳态随机过程.这种假设导致的一个结论是人的行为的时间统计特征是比较均匀的,两个相继行为之间的时间间隔的偏离其平均值很多的概率很小.但是,Barabási通过对用户电子邮件和普通邮件的发送与回复行为的时间间隔的实际统计,展示了与此截然不同的特性:人类行为同时具有长时间的静默与短期的高频率爆发,相邻两个事件的时间间隔分布存在满足反比幂函数的胖尾特性.这些行为的统计特性不能用传统的泊松过程进行描述,说明人类的个体行为可能存在复杂的动力学机制[1].
Barabási等的工作开创了人类动力学的新方向.尽管这个方向问世时间很短,但是由于其理论和应用上的双重价值,很快就吸引了国际上许多知名科学家的关注[2].随即研究者对这一问题展开了极为广泛的探索.Vazqueza[3]认为人类的记忆会对自身的行为产生巨大的影响,因此从人类记忆的角度解释了通信模式中人类动力学的非泊松分布.除此之外,人类行为不仅仅是为了完成某些任务,兴趣爱好往往也是驱动人类行为的一个重要因素,如网页浏览[4-8]、电影点播[9]、游戏[10]等人类行为,所以韩筱璞等[11]提出了一个基于可变兴趣的人类动力学模型,并通过数值模拟和解析进行了研究,得到了指数为1的幂律分布形式的时间间隔分布.
互联网为观察了解和监管人类社会行为的很多方面提供了途径,特别是那种有着大量频繁访问的“老客户”的网站.如果这些网站属于公司或者大学的话,其使用模式能够为人类群体工作习惯提供研究的信息.Dezso等[5]通过研究个体用户的浏览模式和门户网站上某个网页访问量之间的相互作用,发现新闻网页的访问量不依赖于其内容,而主要取决于用户的访问和浏览模式,其访问量表现出幂律衰退特点.Goncalves等[8]对用户浏览网页的日志做了一个基础全面的实证分析,他认为线性优先连接,基于优先权的排队以及用户兴趣的衰减是理解网页浏览行为的关键.张宁[7]用复杂网络的方法研究特定群体进行万维网访问的行为特征,得到了虽然群体用户访问万维网的时间是随机的,所访问的网页各有不同,但大部分人的兴趣是一致的,群体兴趣网络的入度分布具有幂律特征,群体兴趣图谱基本稳定,校园群体上网行为具有特定的时间规律性.本文分别从时间间隔和事件间隔两个层面上研究了某高校的网页浏览日志的规律,群体用户访问网页的时间间隔和事件间隔服从幂律分布,所有单个用户的活跃性也服从幂律分布,而且不论是群体用户行为还是单个用户行为,时间间隔的幂指数大于事件间隔的幂指数.
1 数据来源与统计方法
研究的数据来自国内某高校局域网内师生访问互联网的记录,时间跨度为半个月,从2009年11月26日凌晨0时开始到2009年12月09日凌晨23时59分59秒结束.
对于用户浏览网页的行为来说,最重要的问题是能否有效地判断此过程是由人类发出的正常访问过程.现实中很多因素可以引起页面的发送请求,除了人类用户的正常操作过程之外,还有如良性软件和恶性软件的自动更新过程,黑客的自动攻击.大多数的自动更新过程都呈现出具有清晰频率的规则动态;蓄意攻击的特点是:它们会产生巨大的访问量并且这些访问量会集中在很小的一个时间段内爆发.毫无疑问,这些非正常访问会在实证分析中影响统计结果的准确性.所以文中将使用统计事件间隔的方法来过滤掉统计研究中的非正常访问过程,并且对比事件间隔和时间间隔的统计结果,由此对用户浏览网页的行为进行分析.
统计中定义事件间隔为连续两次访问同一网站期间访问其它网站的次数n,相应的概率分布为P(n).时间间隔t为连续两次访问网页的时间差,相应的概率分布为P(t).统计表明该高校在观测期内一共访问的主站数量为82 153个,平均每天的访问用户有2 631个,平均每天会发出1 510 381个访问请求,较大的数据量足以反映真实的统计规律.
2 网页浏览的行为分析
2.1 群体用户访问网页的时间间隔分布和事件间隔分布
这里所说的群体用户指的是将所有用户看成一个整体,即在不对用户的IP进行过滤的情况下,考察所有用户浏览网页的时间间隔和事件间隔分布.统计结果如图1所示,该分布在双对数坐标下呈现出幂函数的特点,幂指数分别为
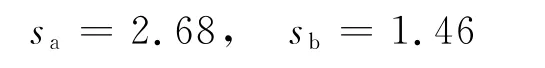
从时间间隔方面来说,随着生活节奏的加快,互联网为人类的生活和学习带来极大的便利,在日常生活和工作中人们常常需要频繁地访问互联网,所以对于群体用户来说,大多数的时间间隔都很短,只有晚上休息的时候才会有比较长的时间间隔,这种时间间隔的极度不均匀性造成了幂律分布的形成.从事件间隔方面来说,这里统计得到的事件个数实际上就是群体用户访问所有网站的个数.由于各种网站的功能不同,所以人们浏览各种网页的概率也不同.如对自己感兴趣的网站,一天可能要浏览多次,高频率的访问必然使得其间访问其它网站的次数减少;而有些跟自己生活不相关的网站,可能很久才浏览一次.这种事件间隔的不均匀性也造成了幂律分布的形成.
2.2 所有单个用户的活跃性分布
文献[9]是众多关于网络应用研究中极具代表性的一项研究成果.笔者对某在线电影点播网站的历史记录进行了研究,提出了“活跃性a”概念,相应的概率分布为P(a).本文也对活跃性进行了实证研究,活跃性定义为用户在一天中平均点击的网页数,用户的平均活跃性
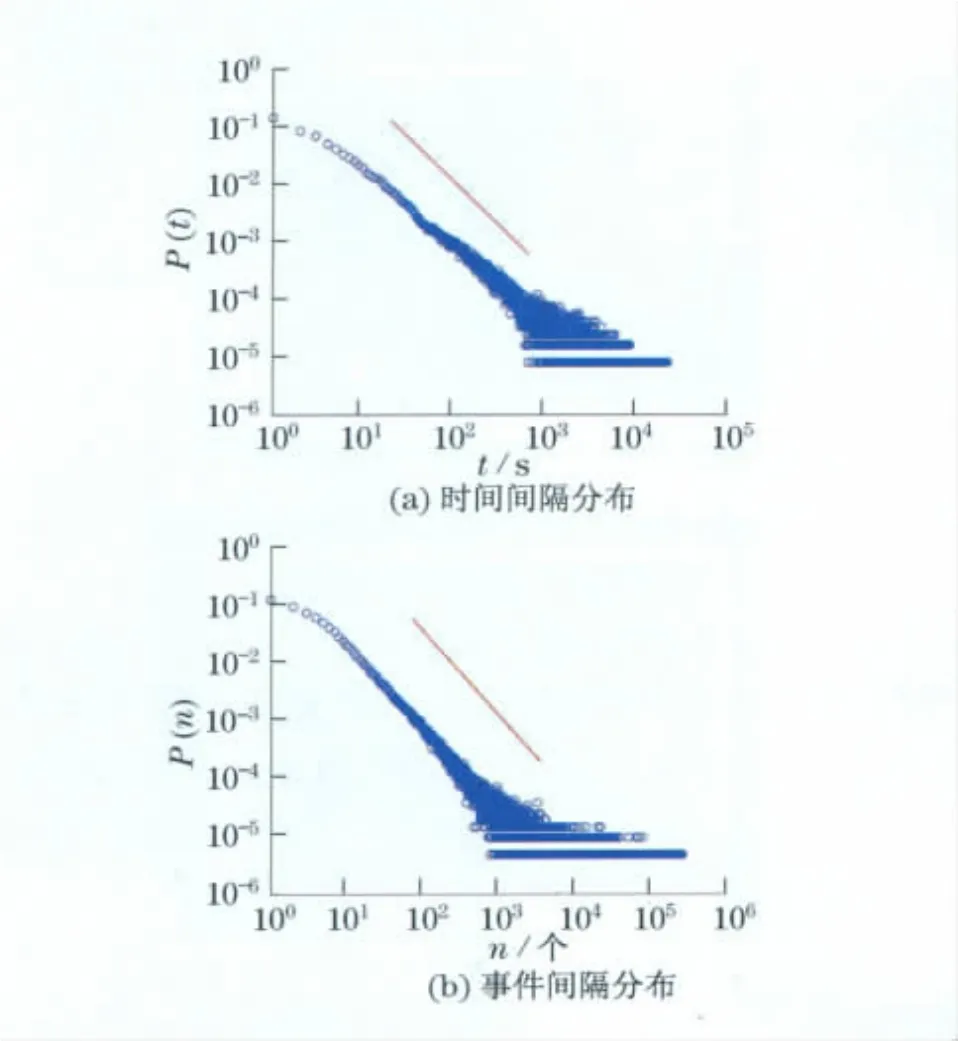
图1 群体用户访问网页的时间间隔分布及事件间隔分布Fig.1 The exponents of time interval and event intervals distributions of web-browsing behaviors based on collective aspects
尽管开始就预测活跃性本身存在着非平凡的分布,但从实证数据中观察到的幂律关系还是让人们感到意外.图2给出了所有单个用户的活跃性分布,幂指数为s=1.68,这与高校的实际生活中的经验相符:多数的学生主要以学业为主,只是偶尔上网娱乐一下或者查阅资料;而少数的学生以搞科研为主,生活学习中离不开电脑,所以上网的活跃性必然比较大.
2.3 幂指数与活跃性的关系
为了挖掘活跃性在人类的网页浏览模式中扮演的角色,将所有用户按照其活跃程度递增进行排序,然后将这些排序后的用户分为20组,每个组包含几乎相同数目的用户.然后对这20组分别进行时间间隔统计和事件间隔统计,并且研究它们的幂指数和活跃性的关系后发现:所有的20组的时间间隔分布和事件间隔分布都满足幂函数律,并且两种统计方法中的幂指数各不相同;时间间隔和事件间隔的幂指数与活跃性都成正相关性.
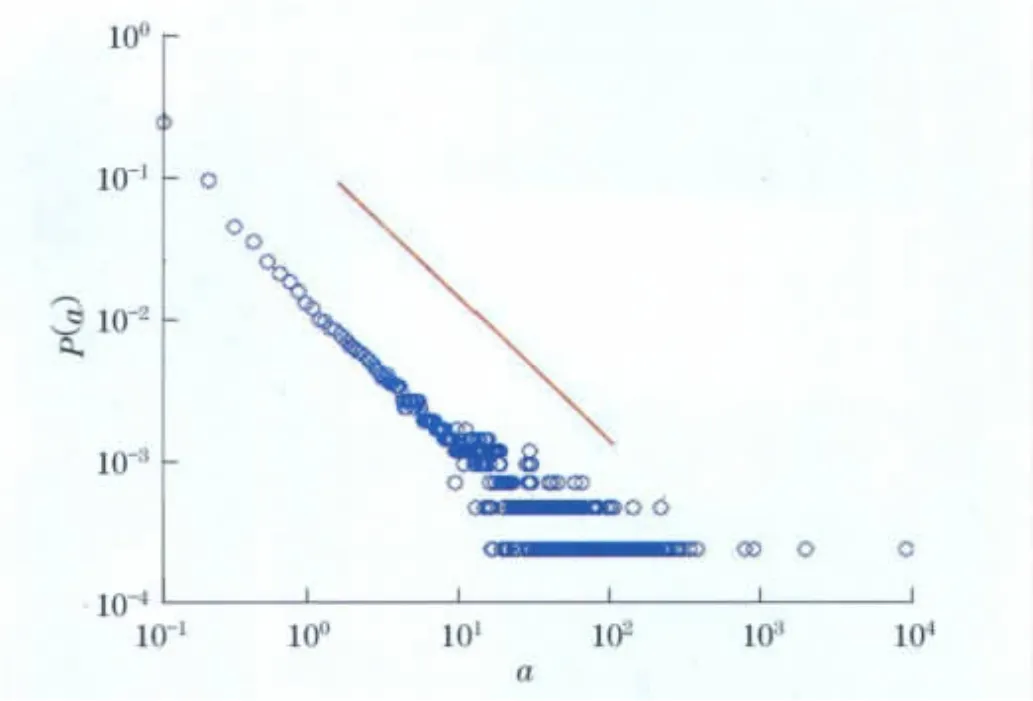
图2 所有单个用户的活跃性分布Fig 2 The exponents of activity distributions of web-browsing behaviors based on all singles aspects
图3(a)为时间间隔的幂指数与活跃性的关系,对其进行曲线拟合发现该分布服从幂律分布,拟合的幂律分布的函数为y=1.037x0.131,拟合指数R2=0.992;图3(b)是事件间隔的幂指数与活跃性的关系,对其进行曲线拟合分析发现该拟合结果服从高斯分布,而不是时间间隔层面中的幂律分布,拟合的高斯分布函数为,拟合指数R2=0.992.
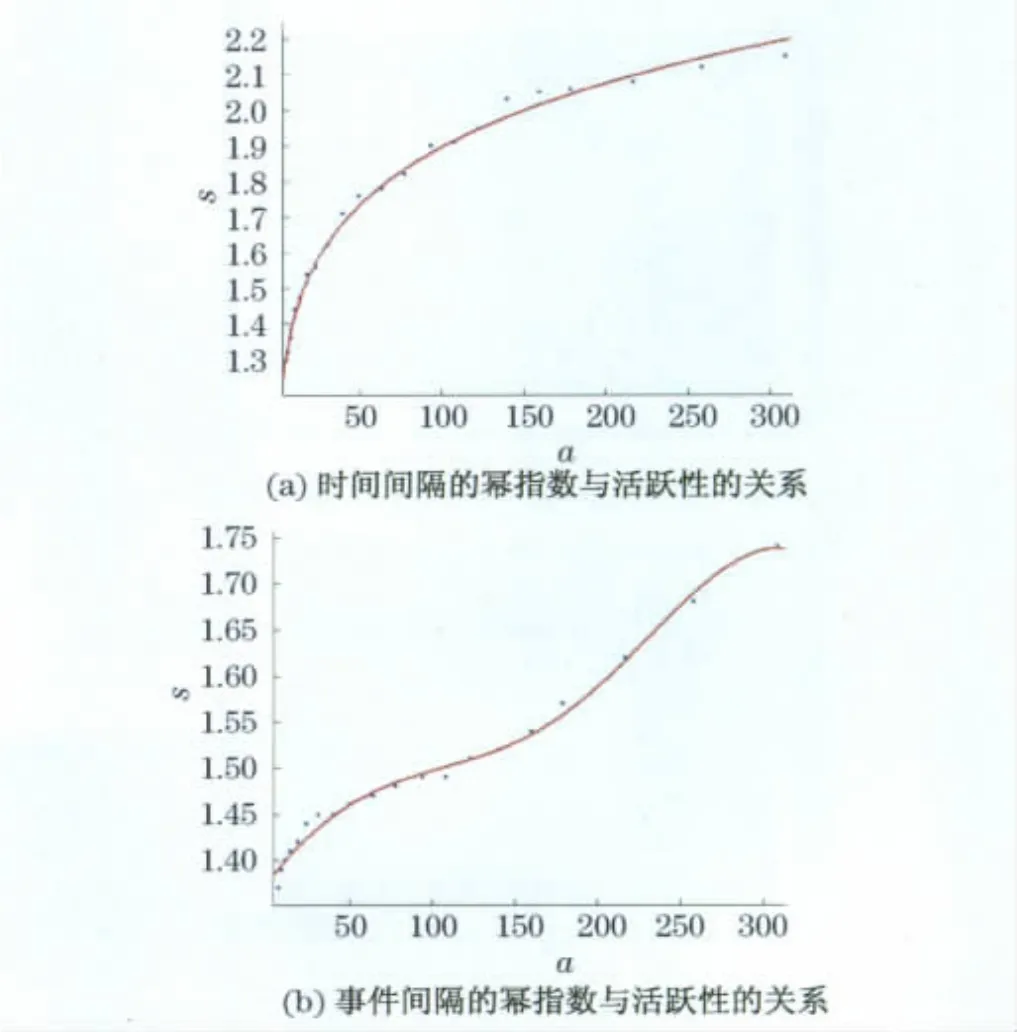
图3 幂指数与活跃性的关系Fig.3 The relation between power-law exponent and activity
2.4 单个用户幂指数分布
为了顾及到每个用户浏览模式的幂指数的不同,本文研究了不同个体的浏览模式并发现单个用户的时间间隔分布和事件间隔分布均服从幂律分布,其幂指数的个体人数c均服从高斯分布.平均幂指数分别是拟合的高斯分布函数分别为y=
从图1中,不难发现群体用户访问网页的时间间隔分布的幂指数大于事件间隔分布的幂指数,而在图4中显示,单个用户时间间隔的幂指数分布的平均指数也大于单个用户事件间隔的幂指数分布的平均指数,并且后者的分布比前者的也要集中.
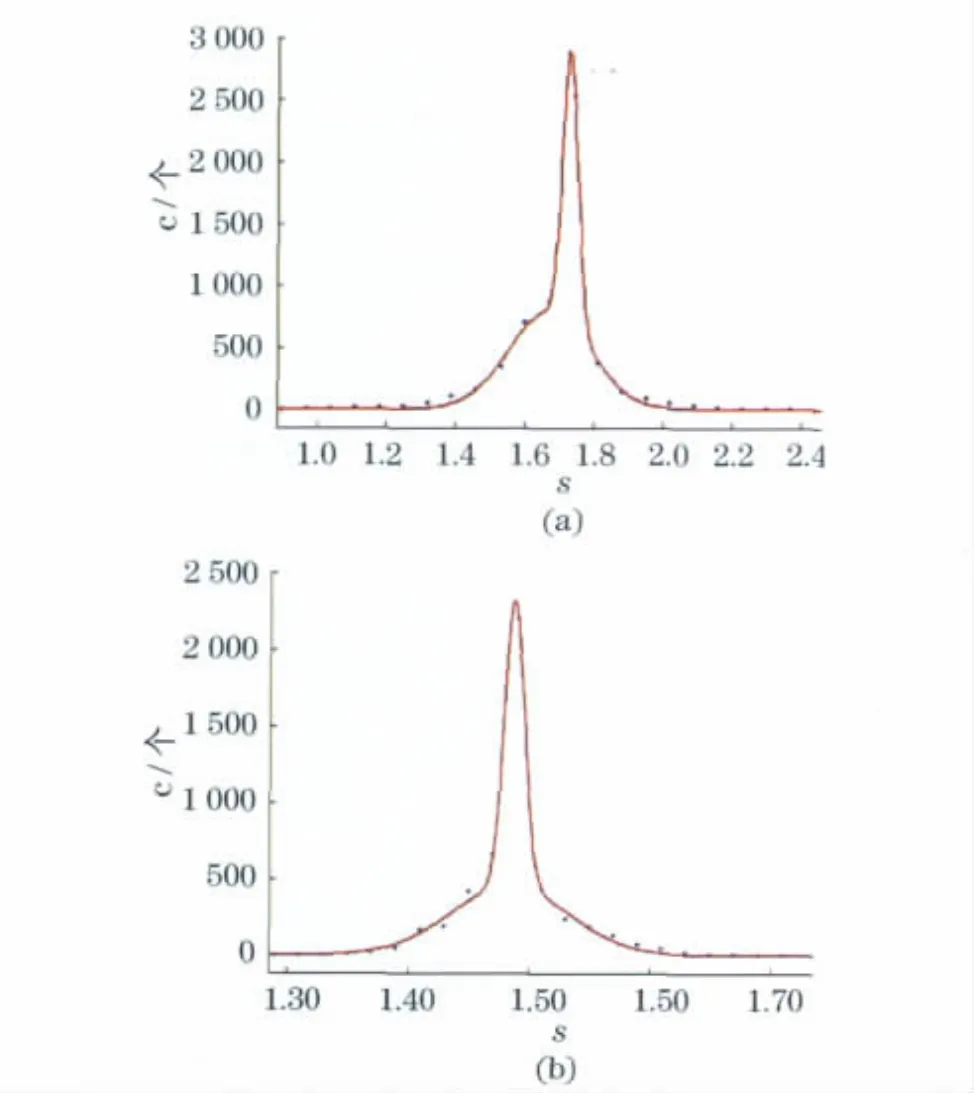
图4 单个用户时间间隔和事件间隔的幂指数分布Fig.4 The time interval distribution is a power law with exponent following a Gaussian distribution,so as the event interval distribution
3 结 论
关于网页浏览的人类行为分析已经有很多专家学者从不同角度进行了分析研究,本文是利用高校访问互联网的历史记录数据,从时间间隔和事件间隔两个层面对群体用户和单个用户进行了分析.实证表明,群体用户访问网页的时间间隔和事件间隔都服从幂律分布,所有单个用户的活跃性也是服从幂律分布的,而且不论是群体用户行为还是单个用户行为,时间间隔的幂指数大于事件间隔的幂指数;时间间隔的幂指数与活跃性服从幂律分布,而事件间隔的幂指数与活跃性服从高斯分布;单个用户时间间隔和事件间隔的幂指数都是服从高斯分布的.
互联网的发展极大的促进了信息的交流和沟通,网页浏览已经成为了人们了解社会动态的一种重要的途径,因此,通过网页浏览模式对人类行为规律的研究,在资源有限的条件下,通过最为恰当的方式,让人人都公平地享有信息资源是非常有必要的.
致谢:感谢中国科技大学韩筱璞和上海理工大学樊超参与的有益讨论.
[1] 汪秉宏,韩筱璞.人类行为的动力学与统计力学研究[J].物理,2010,39(1):28-37.
[2] 李楠楠,周涛,张宁.人类动力学基本概念与实证分析[J].复杂系统与复杂性科学,2008,5(2):15-24.
[3] Vazquez A.Impact of memory on human dynamics[J].Physica A,2007,373:747.
[4] Racz B,Lukacs A.High density compression of log files[DB/OL].[2009-11-10].http://csd12.computer.org/comp/pro2ceedings/dcc/2004/2082/00/20820557.pdf.
[5] Dezso Z,Almaas E,Lukacs A,et al.Dynamics of information access on the web[J].Physical Review E,2006,73(6):066132.
[6] 赵庚生,张宁.人类行为的动力学模型[M].香港:上海系统科学出版社,2008:47-53.
[7] 张宁.群体兴趣网的统计特性研究[J].上海理工大学学报,2008,30(3):243-248.
[8] Goncalves B,Ramasco J J.Human dynamics revealed through Web analytics[J].Physical Review E,2008,78(2):026123.
[9] Zhou T,Kiet H A T,Kim B J,et al.Role of activity in human dynamics[J].Europhysics Letters,2008,82(2):28002.
[10] Henderson T,Nhatti S.Modeling user behavior in networked games[C]//Proc 9th ACM International Conference on Multimedia.New York:ACM Press,2001:212.
[11] Han X P,Zhou T,Wang B H.Modeling human dynamics with adaptive interest[J].New Journal of Physics,2008,10(7):073010.

