基于强化缓冲算子的灰色预测PID控制仿真研究
朱坚民, 黄之文, 翟东婷, 王 军
(上海理工大学机械工程学院,上海 200093)
传统PID控制算法简单、鲁棒性好、可靠性高,广泛应用于工业控制中,尤其适用于可进行精确数学建模的控制系统.但在实际工业控制系统中,某些被控对象存在着不同程度的非线性、大惯性、时变和时间滞后,对于这类被控对象,PID控制不能取得很好的控制效果[1-5].
灰色预测能根据少量系统信息预测系统未来行为,不需要掌握被控对象模型结构的先验信息和控制经验数据,可以实时超前修正控制量,具有很强的自适应性能.将灰色预测理论和传统PID控制相结合,可构成灰色预测PID控制系统.在灰色预测PID控制研究领域,文献[6]提出了一种将传统反馈控制方法和灰色预测控制相结合的新型自调节灰色预测控制器,以此保证控制系统的适应性,获得了更为优良的系统动态性能和鲁棒性.文献[7]将二次型性能指标引入到PID控制器的整定过程中,并按照性能指标的负梯度方向修改加权系数,实现了自适应PID的最优控制律,同时将自适应PID与灰色预测器相结合,显著增强了时变滞后系统的适应性和鲁棒性.文献[8]将提高原始数据序列的光滑性和改变系统行为数据序列的初始条件两者相结合的方法对灰色预测模型进行了改进,以此提高灰色预测控制系统的控制精度.文献[9]提出了灰色预测变参数PID控制,利用迭代学习控制的学习能力来增加控制算法对于周期运动系统的控制精度,使系统的控制性能得到了较明显的改善.文献[10]提出了基于优化背景值和改进初始条件的GM(1,1)模型作为灰色预测模型的自适应PID控制算法,实现了自适应PID的最优控制,使控制系统获得了良好的控制性能.
对于具有较大惯性的被控对象或采样周期和控制周期较小的灰色预测PID控制系统,由于在短时间内控制系统的行为数据变化缓慢,基于采样数据直接建模并进行灰色预测的精度不高,灰色预测PID控制系统不能获得理想的控制效果.针对这个问题,本文提出将强化缓冲算子引入灰色预测PID控制系统,通过对控制系统采样数据的强化缓冲算子作用,提高系统行为数据的变化速率,使灰色预测模型具有更高的预测精度,有效地改善了灰色预测PID控制的效果.
1 控制系统基本原理
常规的灰色预测PID控制系统方框图如图1所示,它是将灰色预测和传统的PID控制相结合,在反馈回路中添加了一个灰色预测器.该预测器是以灰色系统理论为基础,通过灰色预测建模预测控制系统未来的行为趋势,并将其作为控制系统的反馈信号.
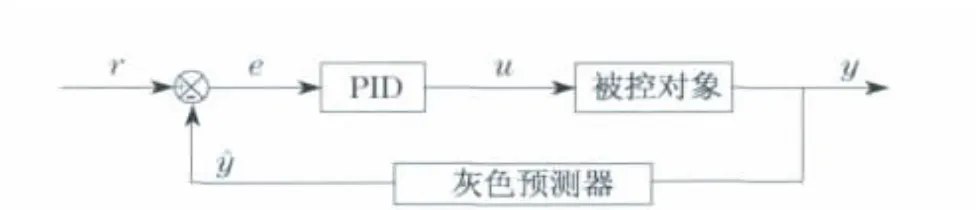
图1 常规灰色预测PID控制系统方框图Fig.1 Block diagram of conventional grey prediction PID control system
在图1中,r为期望输出,e为系统误差,u为控制器输出.反馈回路中的灰色预测器以灰色系统理论为基础,利用当前k时刻之前的n-1个连续的控制系统输出采样数据由灰色预测算法求出k+M时刻的预测值并用预测误差取代经典PID控制系统的误差,进行PID控制的运算.由于利用了误差的预测值进行控制,所以,这种预测控制可以看作是一种“事先调节”,可用于被控对象具有滞后、时变和不确定等特性的实时控制系统.
为了保证对控制系统未来趋势的预测具有较高的灵敏度,预测器的维数一般不能太大.对于实时控制系统来说,预测器的最佳维数为6.对于系统惯性较大或采样周期和控制周期较小的实时控制系统,由于短时间内采样值的变化不大,导致灰色预测器的建模及其预测精度不高.针对这个问题,本文将强化缓冲算子引入控制系统的行为预测,提出了基于强化缓冲算子和GM(1,1)等维新息模型的灰色预测PID控制新方法,控制系统方框图如图2所示.
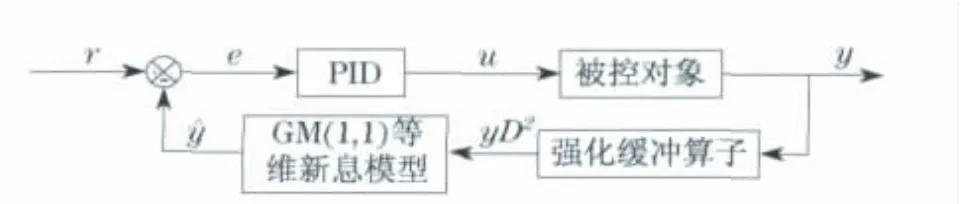
图2 基于强化缓冲算子的灰色预测PID控制系统方框图Fig.2 Block diagram of grey prediction PID control system based on strengthening buffer operator
在图2中,系统的行为数据序列y经二阶强化缓冲算子的作用后得到其二阶强化缓冲序列yD2,D为强化缓冲算子,由此建立GM(1,1)模型,获得控制系统的预测值,计算预测误差再进行PID控制的运算和实时控制.
2 强化缓冲算子的构造
刘思峰等提出了缓冲算子的概念,并构造出一系列强化缓冲算子[11-16],主要可分为两类:平均强化缓冲算子(ASBO)和加权平均强化缓冲算子(WASBO).平均强化缓冲算子虽然可以强化系统行为数据序列,但它是基于系统行为数据序列整体数据的平均作用,没有考虑到系统行为数据序列与各时点的关系,不能精确地反映序列中各数据的重要程度.加权平均强化缓冲算子可以根据系统行为数据序列与各时点的关系,赋予数据序列中各数据信息不同的权值,更好地反映序列的实时性,进一步提高系统的预测精度.对于实时控制系统,越接近预测点的采样数据对控制系统性能的影响越大,应赋予较大的权值;越远离预测点的采样数据对控制系统性能的影响越小,应赋予较小的权值.基于以上要求,本文采用加权平均强化缓冲算子来强化控制系统的实时采样数据序列,提高预测控制的精度.
定理 设X=(x(1),x(2),…,x(n))为系统行为数据序列,第k时刻的权值为wk,k=1,2,…,n.n为序列的维数,则各时点的权重向量为
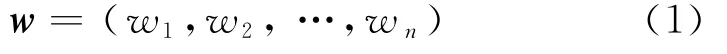
则
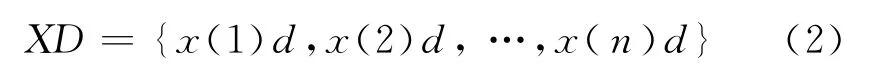
其中
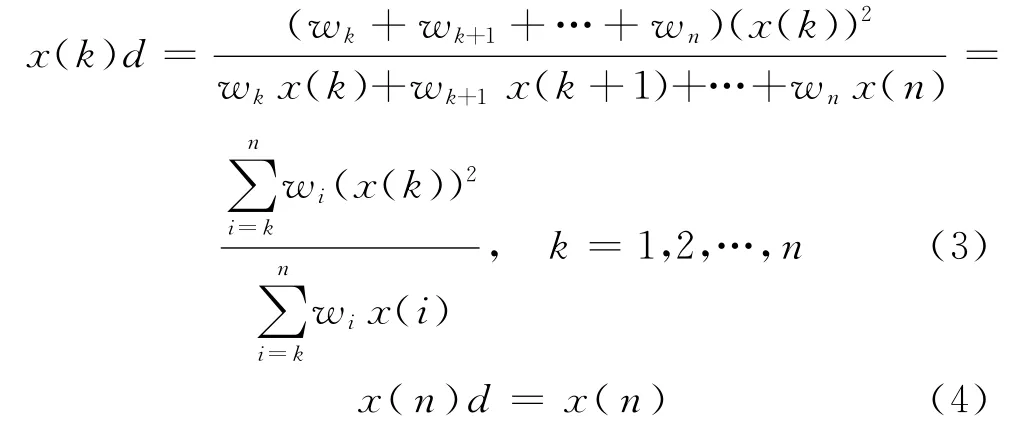
则当X为单调增长序列、单调衰减序列或振荡序列时,D皆为强化缓冲算子.
推论 对于定理中定义的强化算子D,令
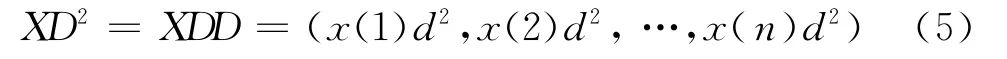
其中
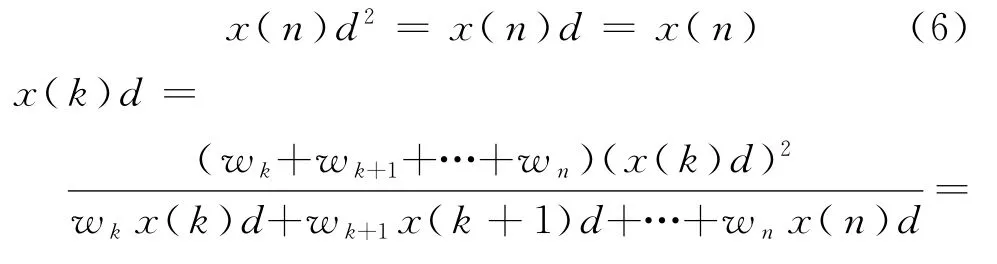
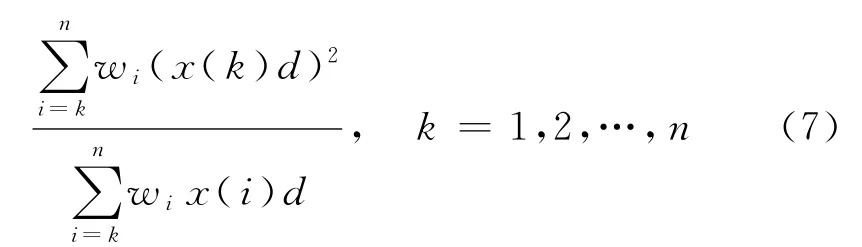
则D2对于单调增长序列和单调衰减序列皆为二阶强化缓冲算子.
从以上定义可知,单调增长序列在强化缓冲算子作用下数据萎缩.由于在缓冲算子作用时,必须要满足不动点定理,即x(n)d=x(n),x(n)d2=x(n),所以,强化缓冲算子作用序列的增长速度比原始数据序列的增长速度加快.同理,单调衰减序列在强化缓冲算子作用下数据膨胀,强化缓冲算子作用序列的衰减速度比原始数据序列的衰减速度加快.因此,当原始数据序列增长(衰减)速度过慢时,利用所构造的强化缓冲算子对原始数据序列进行作用,可使数据序列变得陡峭.因而强化缓冲算子适合于数据序列增长(衰减)速度过慢的情形,且强化算子的构造符合“新息优先”的原则,即最新的信息在强化缓冲算子作用下保持不变.
3 GM(1,1)等维新息预测模型
灰色系统理论的微分方程模型称为GM(grey model)模型.GM(1,1)模型是灰色系统理论中的一种预测模型,表示一阶一个变量的微分方程模型,它将随机过程看作与时间有关的灰色过程,通过对原始数据作累加处理,整理成规律性较强的生成数列进行研究.
对数据列
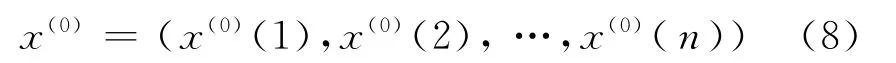
作一次累加(1-AGO)生成数据列为
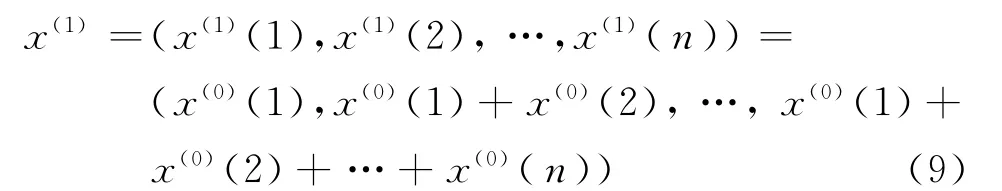
其中
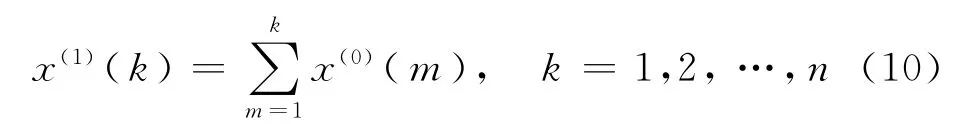
由数据列x(1)建立GM(1,1)模型
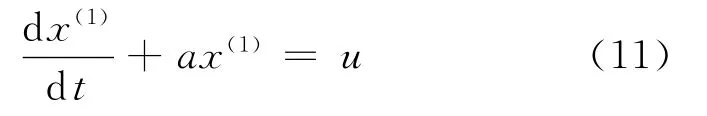
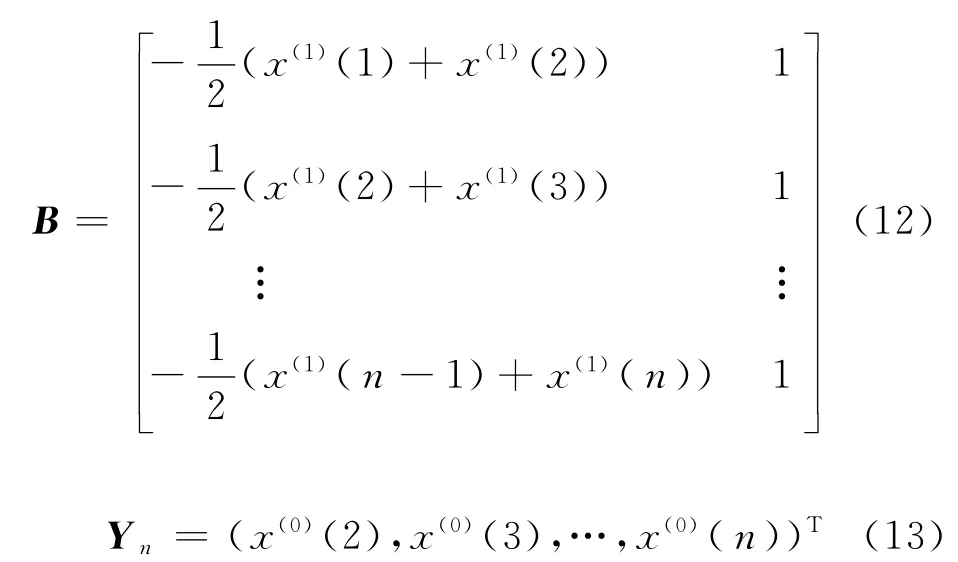
白化形式的微分方程的解为
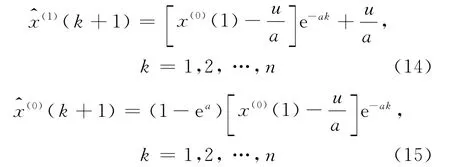
利用式(15)可直接进行预测.
关于等维新息模型的维数,有一个最佳维数区域,其维数并非愈大愈好.一方面,由于灰色模型是基于现有信息来实现对未来的预测,一定数量的已知数据序列对于成功建模是必需的;另一方面,随着采样数据的积累,先期的种种外界条件对现时输出的影响越来越小,剔除当前点某一邻域之外过于陈旧的信息,不仅可以突出最新的变化趋势,而且可以消除预测模型的噪声污染.于是,在此两者之间必然存在着某一适当范围,此范围即为等维新息模型的最佳维数区.最佳维数区与所研究问题的性质和数据序列的特点有关,可通过数值试验来确定.对比实时控制系统的要求,仿真研究表明,预测器的维数取6较为合适[17].
4 控制系统仿真实例
为了验证本文所提出的控制方法的有效性,分别对一阶系统、二阶系统、三阶系统的被控对象的单位阶跃响应进行了仿真研究.仿真之前,必须先确定式(1)所示的各采样点的权重向量.根据灰色等维新息预测理论,用过去和当前的系统行为数据所构成的序列预测未知的系统行为趋势时,越旧的信息对系统行为预测的影响应越弱,越新的信息对系统行为预测的影响应越显著.基于这些要求,本文提出了一种权重系数的构造方法,具体构造过程如下:
设初始权重序列为
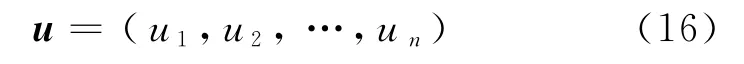
令
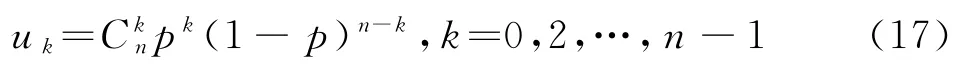
将u=(u1,u2,…,un)中的各元素u1,u2,…,un按从小到大的顺序排列,得到
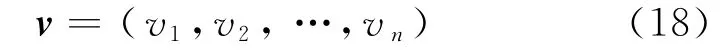
为了提高权重的作用效率,用常数K乘以各权值vi得到
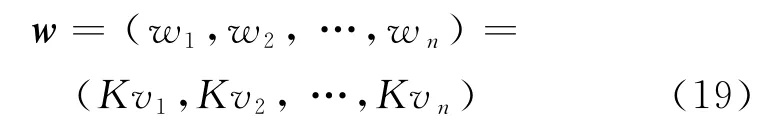
式(17)中p值的取值范围为p∈(0,1),p的具体取值对控制结果的影响不大.在本文的实时控制系统仿真中,取p=0.5,预测建模的维数n=6,并令式(19)中的K=5,得到6个采样点的权重序列为

4.1 一阶系统的单位阶跃控制响应
设被控对象为一阶纯滞后系统,其传递函数为
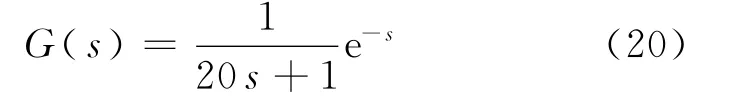
分别采用经典PID控制、传统灰色预测PID控制、基于强化缓冲算子的灰色预测PID控制,研究其单位阶跃响应.图3为一阶控制系统仿真程序.图3中WASBO为加权平均强化缓冲算子,GM(1,1)为6维等维新息灰色预测模型.
仿真结果如图4所示,t为时间.图4中直线1为期望输出,曲线2为经典PID控制的结果,曲线3为常规灰色预测PID控制的结果,曲线4为基于强化缓冲算子的灰色预测PID控制的结果.仿真中的采样时间为1s,预测步长M=1.3种控制器的PID控制参数均相同,kP=0.01,kI=0.05,kD=15.
4.2 二阶系统的单位阶跃控制响应
设被控对象为二阶纯滞后系统,其传递函数为
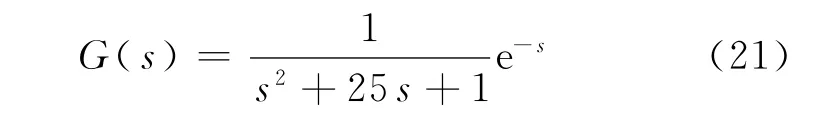
分别采用经典PID控制、传统灰色预测PID控制、基于强化缓冲算子的灰色预测PID控制,研究其单位阶跃响应,仿真结果如图5所示.图5中的直线1为期望输出,曲线2为经典PID控制的结果,曲线3为常规灰色预测PID控制的结果,曲线4为基于强化缓冲算子的灰色预测PID控制的结果.仿真中的采样时间为1s,预测步长M=1.3种控制器的PID控制参数均相同,kP=0.1,kI=0.06,kD=10.
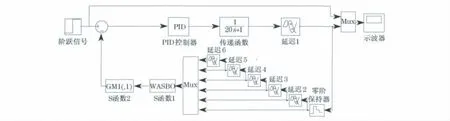
图3 控制系统仿真程序Fig.3 Control system simulation program
4.3 三阶系统的单位阶跃控制响应
设被控对象为三阶纯滞后系统,其传递函数为
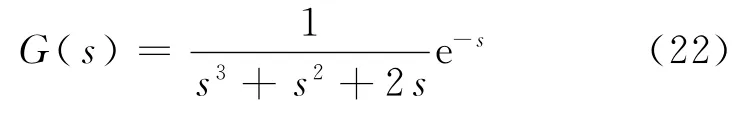
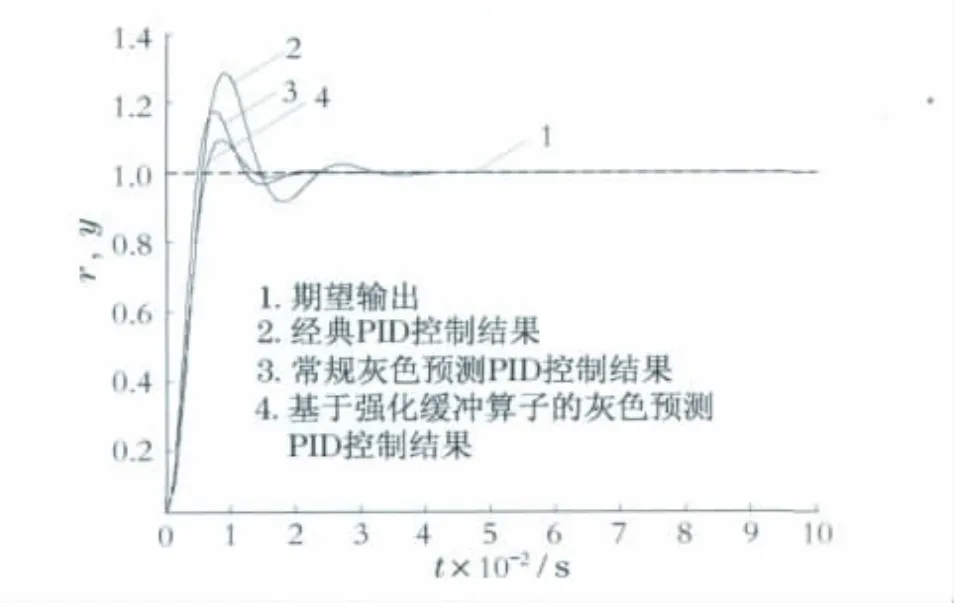
图4 一阶系统的单位阶跃控制响应Fig.4 Unit step response of first-order control system
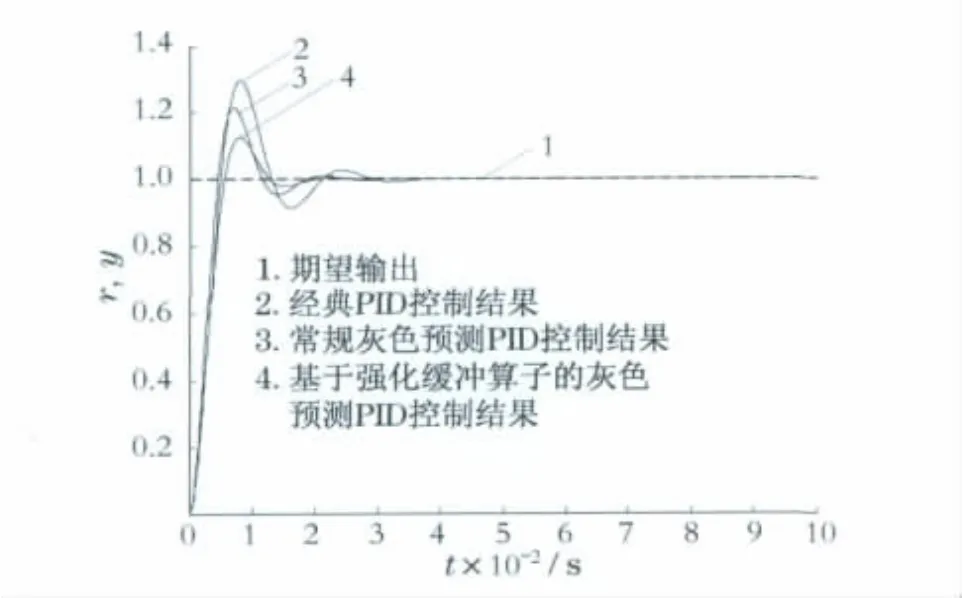
图5 二阶系统的单位阶跃控制响应Fig.5 Unit step response of second-order control system
分别采用经典PID控制、传统灰色预测PID控制、基于强化缓冲算子的灰色预测PID控制,研究其单位阶跃响应,仿真结果如图6所示.图6中的直线1为期望输出,曲线2为经典PID控制的结果,曲线3为常规灰色预测PID控制的结果,曲线4为基于强化缓冲算子的灰色预测PID控制的结果.仿真中的采样时间为1s,预测步长M=1.3种控制器的PID控制参数均相同,kP=0.08,kI=0.003 6,kD=1.
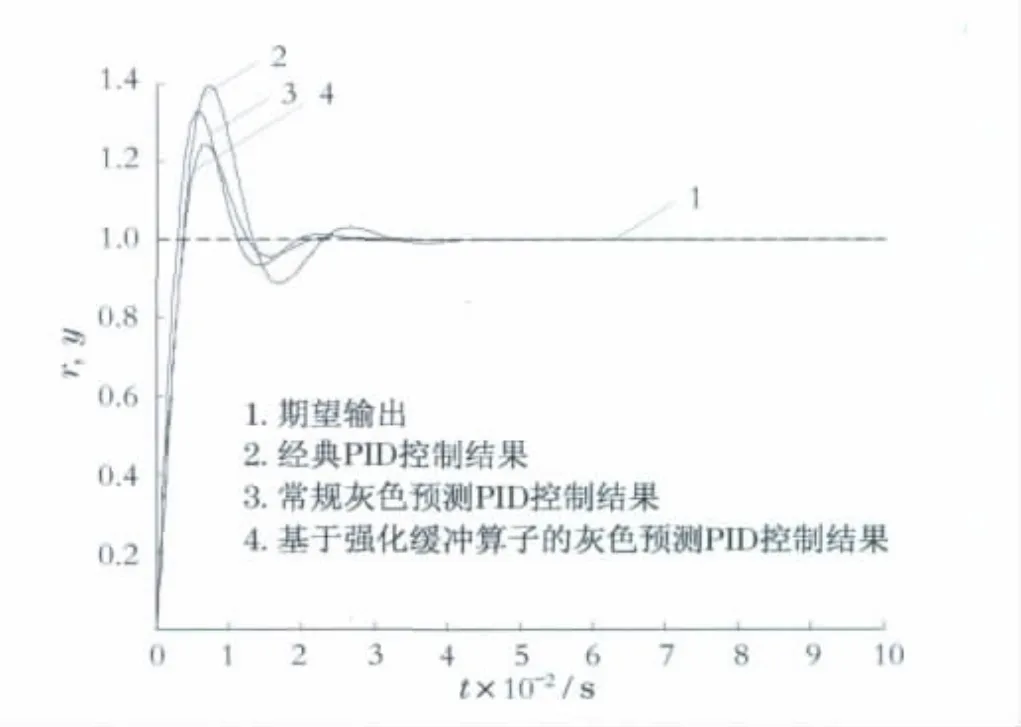
图6 三阶系统的单位阶跃控制响应Fig.6 Unit step response of three-order control system
从上面3个仿真实例可看出,在相同的PID控制器参数下,3种控制方法的稳态精度没有明显的区别.但在动态响应指标方面,基于强化缓冲算子的灰色预测PID控制响应的超调优于经典PID控制响应超调的50%左右,优于传统的灰色预测PID控制响应超调的20%以上,且基于强化缓冲算子的灰色预测PID控制的阶跃响应调节时间在3种控制方法中最短,获得了较好的动态精度.因此,本文提出的基于强化缓冲算子的灰色预测PID控制的控制精度明显优于传统的灰色预测PID控制和经典的PID控制.
5 结 论
a.提出了一种基于强化缓冲算子的灰色预测PID控制新方法.该方法先对控制系统的行为数据序列进行强化缓冲算子作用,再对强化缓冲作用序列进行灰色建模预测,实现了基于强化缓冲算子的灰色预测PID控制.
b.仿真结果表明,在相同的PID控制参数下,基于强化缓冲算子的灰色预测PID控制方法的控制精度明显优于常规的灰色预测PID控制和经典PID控制,获得了理想的控制效果.
c.本文提出的控制方法是可行的、有效的,该方法特别适用于具有较大惯性的被控对象及采样周期较小的控制系统.与常规灰色预测PID相比,控制方法简单,易于实现,控制算法具有较好的实时性.
[1] 李翔,丁振良,袁锋.一类自适应预调节PID控制器的设计[J].仪器仪表学报,2004,25(4):875-876.
[2] 曹刚,俞海斌,徐魏华.大时滞不稳定对象的PID控制[J].仪器仪表学报,2005,26(3):301-304.
[3] 王建国,顾延权,曹广益.时滞系统的最优PID控制与仿真[J].系统仿真学报,2007,19(13):2995-2998.
[4] 张志勇,文桂林.时变时滞系统的灰色预测非线性PID控制[J].系统仿真学报,2009,21(5):2642-2645.
[5] Arrieta O,Visioli A,Vilanova R.PID autotuning for weighted regulation control operation[J].Journal of Process Control,2010,20(4):472-480.
[6] 张广立,付莹,杨汝清.一种新型自调节灰色预测控制器[J].控制与决策,2004,19(2):212-215.
[7] 刘红军,韩璞,姚万业.时变大滞后系统的自适应灰色预测PID控制[J].华北电力大学学报,2004,31(5):44-47.
[8] 吴裕高,朱学峰,史步海.基于灰色预测的大时滞过程的控制研究[J].控制工程,2007,14(3):278-280.
[9] 彭勇刚,韦魏.注塑机机械手位置伺服系统灰色预测PID及迭代学习混合控制[J].仪器仪表学报,2008,29(10):2062-2065.
[10] 刘威,肖军,翟春艳.基于改进灰色预测模型的自适应PID控制算法[J].科学技术与工程,2010,10(2):499-504.
[11] 刘思峰,党耀国.灰色系统理论及其应用[M].北京:科学出版社,2010.
[12] 党耀国,刘斌,关叶青.关于强化缓冲算子的研究[J].控制与决策,2005,20(12):1332-1336.
[13] 谢乃明,刘思峰.强化缓冲算子的性质与若干实用强化算子的构造[J].统计与决策,2006(4):9-10.
[14] 党耀国,刘思峰,米传民.强化缓冲算子性质的研究[J].控制与决策,2007,22(7):730-734.
[15] 王正新,党耀国,刘思峰.变权缓冲算子及其作用强度研究[J].控制与决策,2009,24(8):1218-1222.
[16] Sun Yanna.A kind of practical strengthening buffer operator based on the monotone function[J].Journal of Systems Science and Information,2010,8(2):103-107.
[17] Zhu Jianmin,Zhang Xiaolan,Wu Jingjing.Prediction on stress during bone fracture healing based on equaldimension and new-information model of GM(1,1)[J].The Journal of Grey System,2008,20(3):187-194.

