基于模糊粒子群算法的非线性函数优化

柳 寅， 马 良， 黄 钰

（上海理工大学管理学院 200093）

粒子群算法（particle swarm algorithm，PSA）是一种新型智能优化群体算法［1－2］，这种算法起源于人们对鸟类觅食行为的研究.同遗传算法类似PSA也是一种基于迭代的优化算法.目前PSA已在函数优化、神经网络优化［3］、系统识别［4］等领域有了较广泛的应用.但传统PSA经常在解决实际问题［5－8］时，尤其在解决大规模的问题时容易出现算法过早停滞的缺点，其导致算法陷入局部最优解.本文针对传统PSA的上述缺点提出了改进的算法：使用模糊规则［9－11］引进新的扰动因子改进粒子群算法，简称模糊粒子群算法（fuzzy particle swarm algorithm，FPSA），并通过在典型函数上的测试表明该算法有比较好的全局优化能力.

1 模糊粒子群算法

1.1 粒子群算法基本原理

在传统PSA中，每个优化问题的解都好比是搜索空间中的一只“鸟”，称其为“粒子”.而被优化的函数决定各粒子的适应值，每个粒子同样还有一个决定它们飞翔的方向和距离的速度因素，这决定粒子追随当前的最优粒子在解空间中搜索.

传统PSA的标准进化方程为

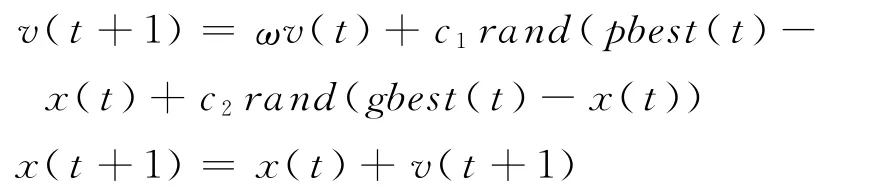
式中，v为粒子的速度；ω为惯性权重；rand为［0，1］之间的随机数；c1，c2为学习因子；x（t）为第t次迭代时粒子的方向.

在每次的迭代过程中，各粒子都通过两个“极值”来更新自己：其一是粒子自身当前迭代过程的最优位置，记为pbest；其二是群体当前迭代过程的最优位置，记为gbest.其中，第i个粒子表示为n维的向量xi＝（xi1，xi2，…，xin），即第i个粒子的位置为xi，每个粒子代表一个可能的解.

1.2 模糊粒子群算法的基本思路

因为传统PSA在全局极值gbest或个体极值pbest得到局部最优解时，粒子群不会在解空间中再次进行搜索，而且其它粒子将迅速向局部最优解靠拢，所以使算法容易出现过早收敛导致不能得到最优解.又因为传统PSA的全局搜索模式相对单一（PSA中仅仅使用全局极值点的信息，而没有加入其它的参考信息，所以使得粒子产生的方式比较单一），这样不利于种群多样性且阻碍算法扩大搜索的范围.

针对上述问题，利用模糊控制器中所使用的模糊规则对传统粒子群算加入了新的扰动因子.在粒子群算法迭代的早期（即迭代计数器NC较小的时候），因为此时算法正处于大面积寻优的初步阶段，所以这个时候不应该让每次迭代更新后的v过大；而伴随着迭代次数的增加，后面逐步加大v.到了粒子群算法迭代的后期（即NC＞3／4 NCmax），大幅度增加v，其v的显著改变对粒子的搜索方向产生较大的影响，这使算法更容易跳出局部最优解，从而更容易获得最优的解.

此外，模糊粒子群算法还利用每次各个粒子所求得的解的质量价值Value，结合NC的大小综合得出干扰因子的大小，而不是每次都仅仅根据NC的大小来决定干扰因子.

对于各个粒子所获得的解的Value，综合NC，以这两个值作为模糊控制器的模糊输入Output.对这两个量进行模糊化划分和模糊量化，然后，确定生成扰动因子的模糊控制规则，最后对输出的模糊量进行反模糊化，最终作用于每个粒子此次的速度更新量.

1.3 模糊粒子群算法流程

首先确定隶属度函数的形状，这里为了方便计算，两个模糊输入变量的隶属度函数都取等腰三角形，输出变量的隶属度函数为棒形单数值函数，模糊语言数目设定5个，即将模糊输入输出空间平均分割成5个模糊集：S（小）、M－（较小）、M（中）、M＋（较大）、B（大），具体见图1.

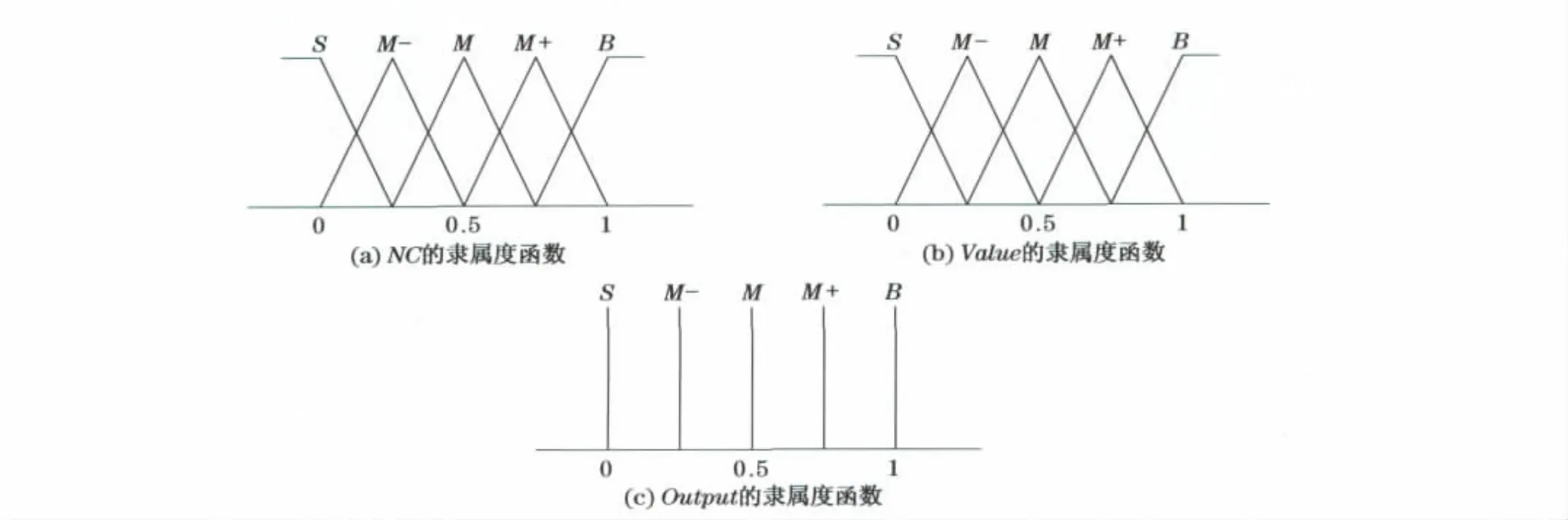
图1 模糊输入输出隶属度函数Fig.1 Member functions of fuzzy input and output

系统模糊规则采用的形式为

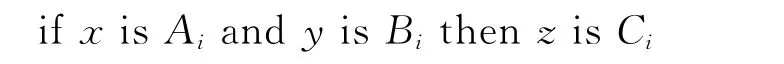
经过大量的实验比较后，具体决定扰动因子生成的模糊规则如表1所示.

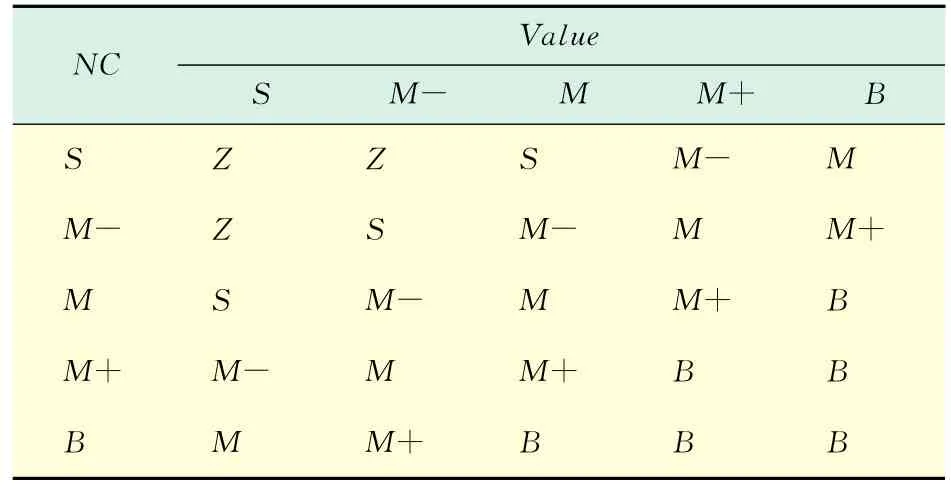
表1 模糊控制规则表Tab.1 Fuzzy rules table

系统有两个输入，有5个模糊值，因此最大的规则基中有5×5＝25条规则.由于后件也有5个模糊值，则前件对后件的规则空间为25×5矩阵.

推理和模糊化方法采用Mamdani推理，重心法.由于输出的隶属度函数是棒形函数，所以重心法在这里就变成了简单的加权平均，由此进一步简化了算法的运算量.

根据模糊规则表中的模糊规则定义，输入的模糊化就是将实际的输入变量从基本论域（［Input1min，Input1max］，［Input2min，Input2max］），转换到模糊输入论域（0，1）.

同理，输出的去模糊化就是将模糊输出论域（0，1）转换到实际的输出基本论域（［Outputmin，Outputmax］），模糊控制规则表图形如图2所示.

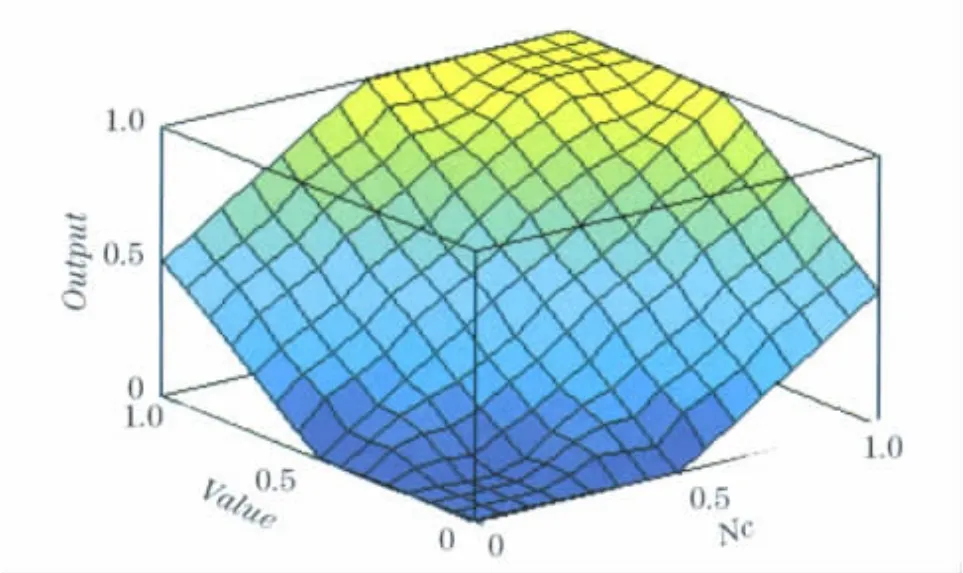
图2 模糊控制规则表图形Fig.2 Image of fuzzy rules table

对于具体的输入（a，b）

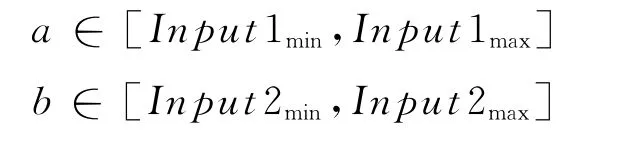
经下式转换为（fa，fb），其中fa，fb∈（0，1）.

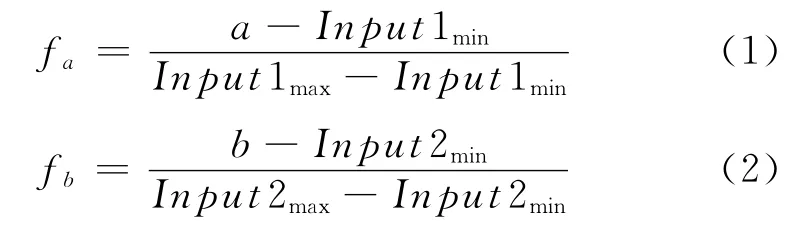
对于输出具体的模糊输出fc，fc∈（0，1），可转换为

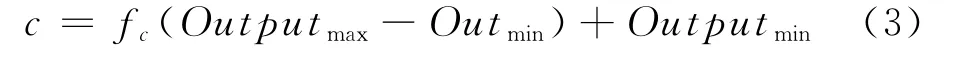
其中，c∈［Outputmin，Outputmax］.

模糊粒子群算法流程：

步骤1 随机初始化粒子群中粒子的位置与速度；

步骤2 将粒子的pbest设置为当前位置，gbest设置为初始群体中最佳粒子的位置；

步骤3 判断算法停止准则是否满足，如果满足，转向步骤7，否则执行步骤4；

步骤4 按照模糊粒子群算法的更新机制更新各粒子的速度和移动方向，更新方程为

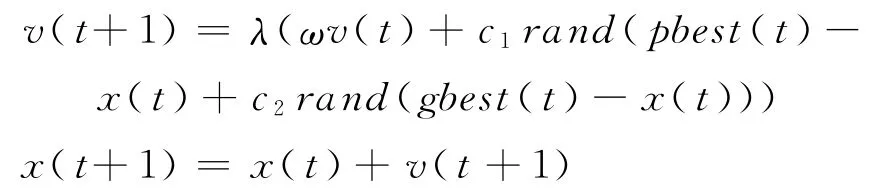
其中，λ为反模糊化后的模糊输出值（扰动因子）.

步骤5 更新所有粒子经历过的最好位置，即全局极值gbest（如果可行粒子的目标函数值优于gbest的目标函数值，gbest设置为新位置）；

步骤6 判断算法停止准则是否都满足，如果满足则转步骤7，否则执行步骤4；

步骤7 输出gbest，算法停止.

2 算例测试

为了验证算法的可行性和有效性，选取了一系列经典函数进行测试实验.参数设置：种群规模设定为20～80个、c1＝c2＝2、ω＝0.8、最大迭代次数为100.实验所用硬件为AMD 2.0GHz，2GB RAM，软件为Windows XP和Matlab 2008.

算例1（Griewank函数）

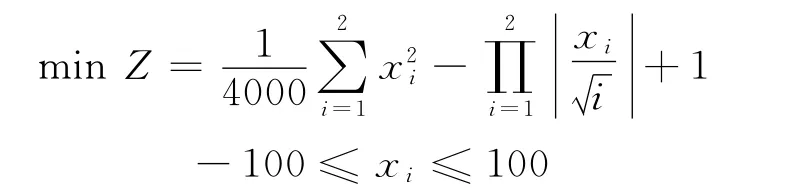
此函数为漏斗形状，最小极值点位于图像最中央.采用遗传算法遗传200代后的结果为0.093 22.LINGO软件所得到的目标值为0.623 42，Matlab优化工具箱得到的结果为0.060 31，模糊粒子群算法得到的最优解为0，（x，y）＝（0，0）.Griewank函数图像由图3所示.

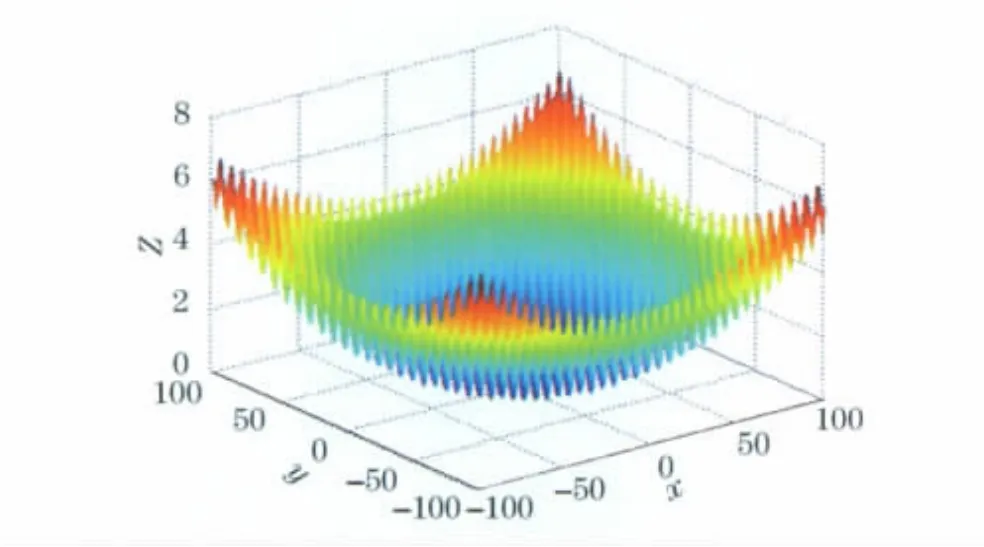
图3 Griewank函数图像Fig.3 Image of function Griewank

算例2（Schaffer函数）

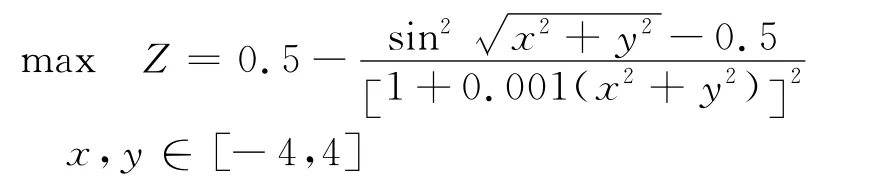
混沌优化方法所需计算次数为1 092，混沌遗传算法所需计算次数为458.LINGO软件所得到的目标值为0.646 848 8［11］，Matlab优化工具箱得到的结果为0.990 3，模糊粒子群算法得到的最优解为1，（x，y）＝（0，0）.Schaffer函数图像由图4所示.

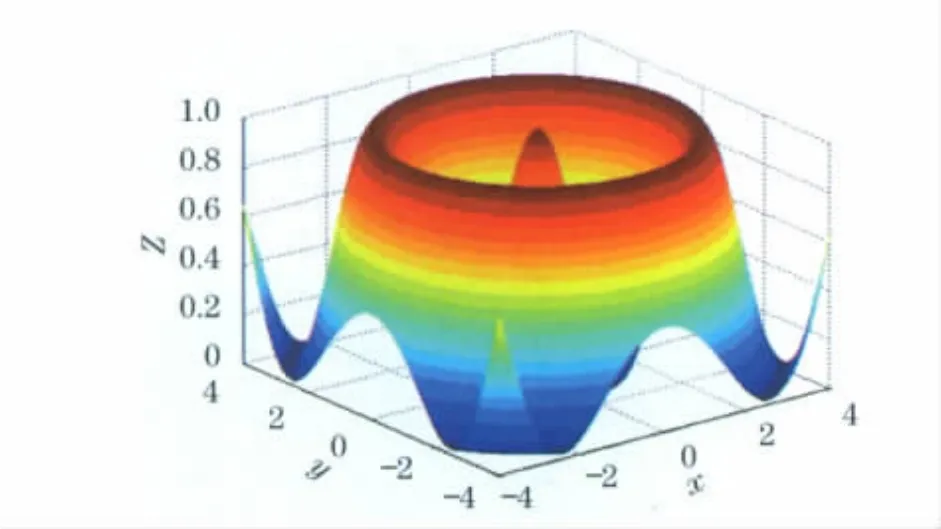
图4 Schaffer函数图像Fig.4 Image of function Schaffer

算例3（Hansen函数）

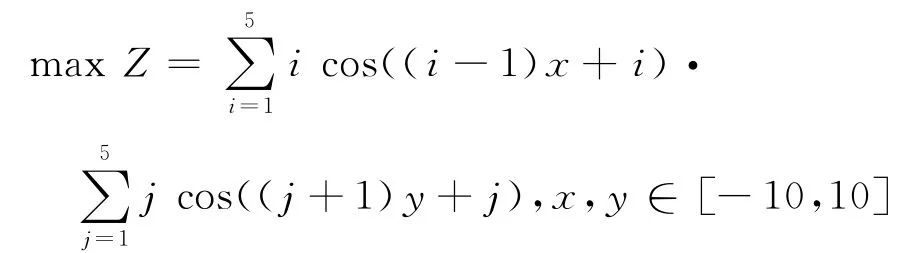
此函数局部极值点有760个.LINGO软件得到的结果为12.354 7.Matlab内部函数所得到结果与初值有关，初值取得好，则可得到最优解，有不确定因素的存在［11］.遗传算法100代内可得到最优解.

模糊粒子群算法可以得到全局最优值为176.541 793，并经多次反复运行，可找到全部最优解（－7.589 893，－7.708 314），（－7.589 893，－1.425 128），（－7.589 893，4.858 057），（－1.306 708，－7.708 314），（－1.306 708，－1.425 128），（－1.306 708，4.858 057），（4.976 478，－7.708 314），（4.976 478，－1.425 128），（4.976 478，4.858 057）.Hansen函数图像由图5所示.

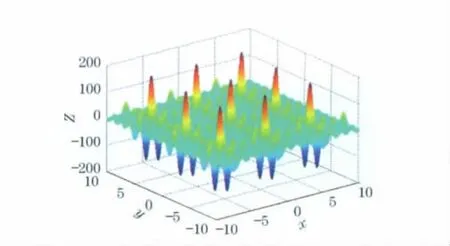
图5 Hansen函数图像Fig.5 Image of function Hansen

算例4（大海捞针问题）

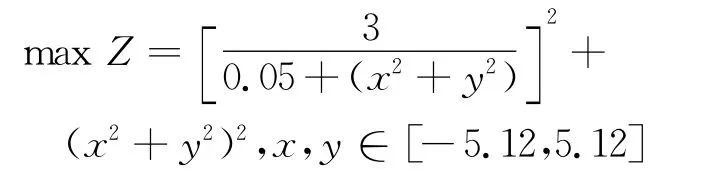
该问题的全局最优解被最差解包围，4个局部极值点为：（－5.12，5.12），（－5.12，－5.12），（5.12，－5.12），（5.12，5.12），函数值为2748.78.LINGO和Matlab内部函数，都会落入上述4个局部极值点中.采用有一定技巧的遗传算法在遗传300代后才能以90%的几率获得最优解，运行模糊粒子群算法可得到最优解：3 600，（x，y）＝（0，0）.算例4函数图像由图6所示.

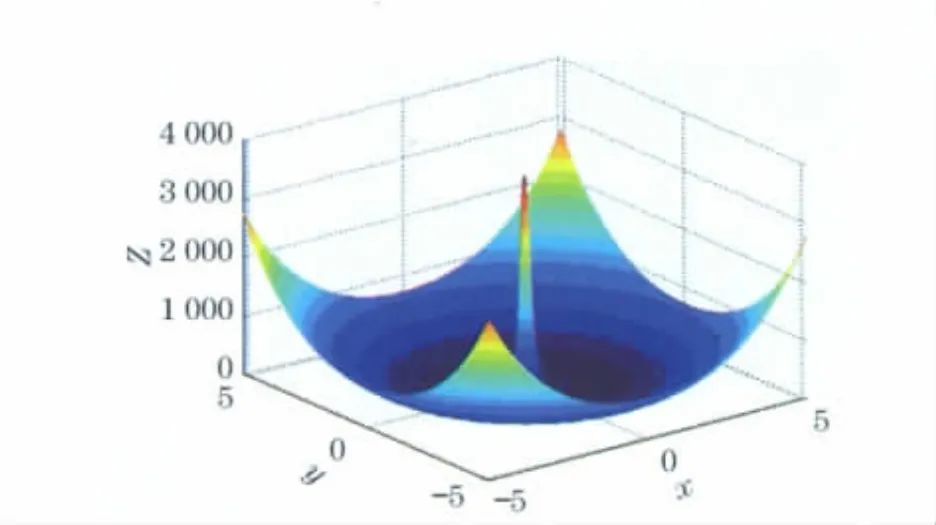
图6 算例4函数图像Fig.6 Image of function 4

从以上的算例可以看出，模糊粒子群算法具有更有效地获取全局最优解的能力.

3 结束语

通过运用模糊控制器中的模糊规则为传统粒子群算法加入了新的扰动因子，改进了粒子群进化的更新方程，利用该方程更新粒子的速度与位置，不仅避免了过早收敛问题，而且还扩大了群体的搜索范围.通过实例验证表明了该算法的有效性.对此方法中涉及参数地指导性调整将是进一步研究的课题.

［1］ Kennedy I，Eberhart R C.Particle swarm optimization［C］／／Proc IEEE Int Conf On Neural Networks.Perth，1995：1942－1948.

［2］ Shi Y，Eberhart R C.A modified swarm optimizer［C］／／IEEE international conference of Evolutionary Computation.Anchorag，1998：125－129.

［3］ Bergh F，Engelbrecht A P.Cooperative learning in neural networks using particle swarm optimizers［J］.South African Computer Journal，2000，11（6）：84－90.

［4］ Voss M S，Feng X.A RMA model selection using particle swarm optimization and AIC criteria［C］／／15th Triennial World Congress.Barcelona：IFAC，2002：41－45.

［5］ Andrews P S.An investigation into mutation operators for particle swarm optimization［C］／／Proceeding of the 2006IEEE Congress on Evolutionary Compu－tation.Toronto，2006：1044－1051.

［6］ 李炳宇，萧蕴诗，吴启迪.一种基于微粒群算法求解约束优化问题的混合算法［J］.控制与决策，2004，19（7）：804－807.

［7］ 于繁华，杨威，张利彪.基于模糊的多目标粒子群优化算法及应用［J］.计算机仿真，2007，24（2）：53－156.

［8］ 柳寅，马良.模糊蚁群算法及其在TSP中的应用［J］.数学的实践与认识，2011，41（6）：150－154.

［9］ Takagi T，Sugeno M.Fuzzy identification of systems and its applications to modeling and control［J］.IEEE Trans Sys Man：Cybernetics，1985，15（10）：116－132.

［10］ Khaled B，Fzouzi T.Genetic algorithm for the design of a class of fuzzy controllers：an alternative approach［J］.IEEE Trans：Fuzzy Systems，2000，8（4）：398－405.

［11］ 丁建梅，王可崇.基于MATLAB的模糊控制器控制规则优化研究［J］.哈尔滨工业大学学报，2004，10（3）：45－50.

［12］ 马良，朱刚，宁爱兵.蚂蚁优化算法［M］.北京：科学出版社，2008，190－194.