CHMM语音识别初值选择方法的研究

刘伶俐， 王朝立， 于 震

（上海理工大学光电信息与计算机工程学院，上海 200093）

隐马尔科夫模型（HMM）作为语音信号的一种统计模型，语音识别效果好，能够很好地描述语音信号的特点，在数字语音处理中应用非常广泛.

HMM包括离散的模型（DHMM—Discrete HMM）、连续混合密度模型（CHMM—Continuous HMM）以及半连续模型（SCHMM—Semi－Continuous HMM）.相比较DHMM，CHMM系统识别率更高，这是由于在CHMM中输入向量X即观察值向量，不需要经过矢量量化转变，这个输入向量直接就是每一帧语音信号的特征矢量.基于CHMM系统识别率高的特点，它的应用非常广泛.文献［1］给出了基于性别的CHMM语音识别方法，文献［2］研究了驾驶员意图识别的可能性，文献［3］讨论了基于声音的轴承故障诊断等.

在HMM模型建立后用Baum－Welch迭代算法求解HMM模型，其中一个重要的问题就是初始模型的选取［4］，不同的初始参数模型将产生不同的训练结果与识别结果.关于DHMM初值的研究，文献［5］说明了DHMM初始参数选择的一般规律和最佳选择方法，但是CHMM的初始参数至今还没有一个最佳的选择方法.传统CHMM参数初始化方法是随机分布之值、K均值算法，但是由于K－means方法存在对初始中心的依靠较重、对孤立点影响较大和聚类结果不稳定的缺点［4，6］，因此，有人提出了对初值中心选择的改进方法：基于密度的方法［7］和最大最小距离法［8］.基于密度的方法首先去除孤立点，在密度所在的区域内随机选择初始中心，但是密度相似性大小相差较大时，聚类结果不好；而最大最小距离方法虽然可以使类间相似性最弱，类内相似性最强，但是忽略了孤立点对聚类结果的影响.

本文在研究连续混合密度模型（CHMM）初始参数选择时，为了更好地平滑逼近语音特征，使语音特征矢量类间相似性最小，类内相似性最大，采用最大距离选择初始聚类中心、最小距离将语音特征矢量分类、平均距离去除类内干扰点的K－means方法.这种方法不仅去除了聚类中的干扰点，而且克服了传统算法的缺点，为语音训练识别节省了时间，提高了语音的识别率.

1 CHMM的基本元素

设S＝｛Si｝，i＝1，2，…，N，为模型的N状态空间，CHMM常用M＝｛S，X，A，B，π，F ｝6个模型参数来定义，不过一般简化用M＝（A ，B，π）表示.

A表示状态转移概率矩阵，A＝｛aij｝，aij＝P［qt＋1＝j｜qt＝i］，1≤i，j≤N，q为状态序列；B表示概率密度分布函数集合，B＝｛bj（X）｝，1≤j≤N；X为观察向量；π表示系统初始状态概率的集合，πi表示初始状态是qi的概率即πi＝p ［q1＝i］，1≤i≤N；F为系统终了状态矩阵.

2 CHMM模型

研究对象选取连续的无跨越自左向右的CHMM，观察参数矢量为X＝x1，x2，…，xT，状态序列为q＝q1，q2，…，qn，状态数为N，CHMM初始模型为λ＝（A，B，π）.

一般认为π和A初值的选取对结果的影响不大，但B的初值对HMM的影响比较大［6］.所以本文主要研究B的初值对CHMM的影响.

无跨越自左向右的CHMM，由于输出的是连续值，不是有限的，所以不能用矩阵表示输出概率［4］，而用概率密度函数来表示，即用bj（X）表示.bj（X）称为参数X的概率分布函数，输出X的概率可以通过bj（X）计算出来.一般bj（X）用高斯密度函数表示，由于X是多维矢量，所以用多元高斯概率密度函数表示为

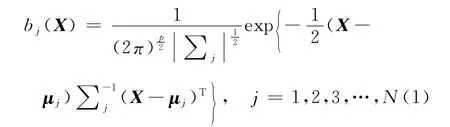
这里p是X的维数，μj是概率密度的均值矢量，T为转置，∑j是概率密度的协方差矩阵（为计算方便一般用对角协方差矩阵）.

在实际的语音信号处理系统中，往往用一个高斯概率密度函数不足以表示语音参数X的输出概率分布，所以常采用混合模型将所有的局部特征综合在一起，形成一个更为全面的分布函数.这里使用多个高斯概率分布的加权组合，表示输出概率密度函数［4］为

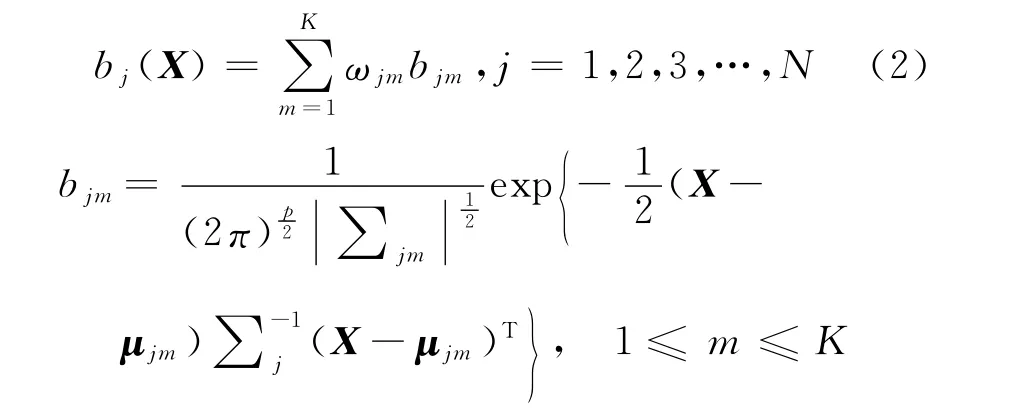
这里ωjm是混合系数，又叫分支概率，即第m个分量权重，满足为分支概率密度，即表示状态为j的第m个分量的高斯概率密度函数.μjm和∑jm是状态j中第m个混合分量的均值矢量和协方差矩阵.

bj（X）概率密度特性满足由式（2）可以看出，混合概率密度函数由各个概率密度函数组合而成，概率密度函数可由均值矢量、协方差和混合分量来描述.为求得输出概率密度必须要先确定初值μjm，∑jm，ωjm，这对后面参数的重估至关重要.对各状态的混合高斯函数的均值、方差和权系数的初始化，传统采用K均值算法.

2.1 传统初始化方法

K－means算法以每类的均值矢量和协方差矩阵为类中心作为分类准则度量，则最终k个高斯分量的均值估计和方差估计即为每类数据的均值矢量和协方差矢量.

具体步骤如下：

a.由某一状态的训练语音，随机选取k个点（即特征矢量），每个点代表一个类的初始中心或平均值；

b.其余点根据相似度准则（欧氏距离）将相同或相似的数据归为一类；

c.如果相邻的两次聚类中心没有任何变化，说明对象调整结束，否则调整新的聚类中心，重复b；

d.计算每一类的均值矢量，作为高斯概率密度函数的均值估计和高斯概率密度函数的初值.

以上是传统的计算方法，优点是过程简单、操作容易.但是这种方法有很大的缺点：第一，由于初始聚类中心是随机选取，所以不同的初始中心可以得到不同的初始均值和方差，造成不同的局部最大，聚类结果稳定性较差；第二，K－means算法对噪声和孤立点数据比较敏感.

2.2 一种改进的CHMM参数初始化方法

基于传统算法的缺点，本文提出一种改进算法：首先选择相互距离最远的k个对象作为初始聚类中心；然后按相似性最强分类，为不受干扰点的影响，聚类结束后去除每类中的干扰点.这样的好处是所选择的初始中心更具有代表性，使得类内相似性最强，每类均值特征与语音特征偏离度较小，能更好地平滑逼近语音特征.

从式（1）中可以看出，bj（X）由均值和协方差矩阵决定，其实主要由均值决定.假定δii（x）是协方差矩阵中的元素，δii（x）表示X与μj（x）的偏离程度，按输出概率密度最大来说，一般总希望δii（x）应尽可能的小（但不能为零），这样X与μj（x）越接近，bj（X）就越大.

令

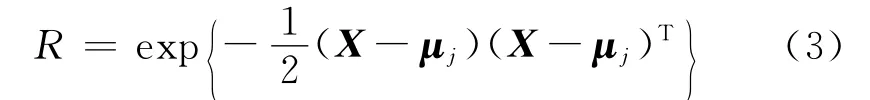
由式（3）可以看出，当X与μj（x）的偏离程度最小时，说明它们的相似性最强，即每个概率密度函数也就取得最大值，根据这个原则定义相似性.

定义1 样本X中的元素xi是p维的，一个样本特征向量与另一个样本特征向量之间的相似性公式为

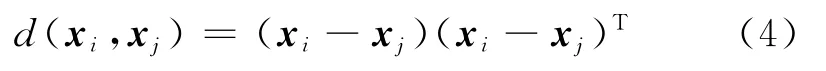
d的数值小说明xi，xj的相似性强，反之它们的相似性弱.式（4）选择的是欧式距离的平方，相似性的判别与欧式距离相同，但是算法的效率要比欧式距离高.

该算法主要有3步：一是求距离；二是分类；三是去除干扰点.将样本分为k类的具体算法描述如下：

a.某一状态的训练语音X＝x1，x2…xt，按式（4）分别计算两两特征矢量（点与点间的）距离，各特征矢量间相互独立；

b.选出距离最大的两个点（xi，xj）作为两个初始中心y1＝xi，y2＝xj，将X中的其余点以y1，y2为初始中心按式（4）求取距离，按最小距离的原则将X分为D1，D2两类；

c.在D1，D2中找出与y1，y2相似性最弱的特征向量xi，xj，并分别代入式（4），得到d＝max（max d（y1，xi），max d（y1，xj），max d（y2，xi），max d（y2，xj）），将距离最大的xi（xj）作为y3，并以y3为中心按式（4）分类；

d.在已经找到的m个初始中心共有D1，D2，…，Dm类，按式（4）寻找与初始中心最远的点，并按max（max d（yi，xi），max d（yi，xj），max d（yj，xi），max d（yj，xj））选下一个初始中心，并重新划分归类，直到分为k类；

e.分类结束后，计算每类中其它点与聚类中心的距离，并求平均距离，将与聚类中心距离大于平均距离的点从此类中删除；

f.将每类中的剩余点计算均值；

g.ωjm的值等于每类中的特征矢量个数，除以所有类中特征矢量个数之和.

以上算法是按两点之间相似性的大小，进行初始聚类中心的选择，有一定的规律性，克服了一般K－means的初值选择无序的状况；而且根据所定义的相似性公式所选的初始聚类中心满足协方差偏离程度最小，并且删除了每类中的干扰点，这样所得的均值向量与特征值向量相似性最好，聚类效果好，有利于参数的估计和语音的识别.

3 不同CHMM参数初始化方法对识别结果的影响

连续无跨越自左向右的CHMM，系统初始状态概率的集合为π＝［1，0，0，…，0］，即从第一个状态开始执行.状态转移概率矩阵A，aij为A中的元素，0＜aij＜1，满足

转移概率矩阵初值选择

B的初值分别由传统K－means方法与改进后的K－means方法进行选择.对于传统K－means方法随机选择初始聚类中心，然后按最小距离准则对输入样本分类，更新聚类中心，通过迭代最后得到初始参数；而对于改进的K－means方法先按照最大距离选择k个相似性最弱的点，然后按最小距离准则对输入样本分类，更新聚类中心，最后将每类中的孤立点去除，计算每类的均值矢量、协方差矩阵以及混合权值作为初始参数.

实验是在matlab 7.0环境下实现，语音样本为非特定人孤立数字0～9共400个.每个数字录音40个，其中20个用于语音训练，20个用于语音识别.采用不同的初始化方法进行语音识别所得到的识别率结果如表1所示.

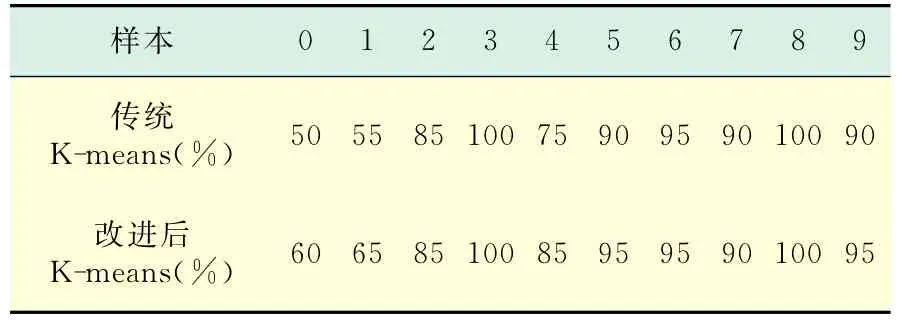
表1 不同参数初始化方法Tab.1 Different parameters initialization ways

从表1可以看出，采用改进后的K－means算法所得到的CHMM初始参数得到的识别率更好，这是因为此方法克服了传统算法的缺点，并去除了干扰点对识别结果的影响.

4 结 论

研究了CHMM的初始参数概率密度函数的选择，在传统的初值选择方法的基础上提出了改进后的K－means方法.在规定的条件下，改进后的初值选择方法，克服了语音在初值的选择上不稳定性和孤立点的影响，更逼近语音特征，提高了聚类的准确性和语音的识别率.

［1］ 张捍东，李金炜.基于性别识别的分类CHMM语音识别［J］.计算机工程与应用，2007，21（7）：187－189.

［2］ Jin L S，Hou H J，Jiang Y Y.Driver intention recognition based on continuous hidden Markov model［C］／／International Conference on Transportation，Mechanical，and Electrical Engineering（TMEE）.Changchun，2011：739－742.

［3］ Wu B，Wang M J，Lou Y G.Cyclostationarity and CHMM based bearing fault diagnosis approach in start－up process［C］／／2010 2nd International Conference on Computer Engineering and Technology（ICCET）.Chengdu，2010：433－436.

［4］ 赵力.语音信号处理［M］.北京：机械工业出版社，2008.

［5］ 马明，张杰，王建宇，等.语音识别中隐马尔科夫模型初值的估计［J］.数据采集与处理，1997，2（7）：96－100.

［6］ 韩纪庆.语音信号处理［M］.北京：清华大学出版社，2004.

［7］ 汪中，刘贵全，陈恩红，等.一种优化初始中心点的K－means算法［J］.模式识别与人工智能，2009，2（4）：299－304.

［8］ 苏中，马少平，杨强.基于Web－Log Mining的Web文档聚类［J］.软件学报，2002，13（1）：99－104.