一类耦合KdV方程的孤波解和周期波解及其相互关系
张卫国, 徐 伟, 李 想
(上海理工大学理学院,上海 200093)
1 问题的提出
耦合KdV波动方程[1]
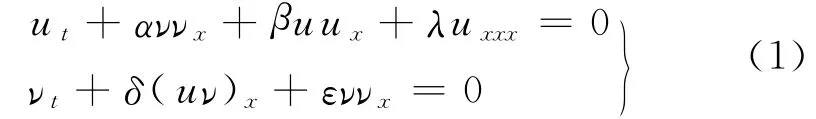
可用来描述两个内部长波之间相互作用的过程,其中α,β,λ,δ,ε为非零参数.在变量ν=0时,方程(1)可约化为在固态物理、等离子物理、流体物理和量子理论等领域有广泛应用的KdV方程[2-7].
近年来,多位学者研究了方程(1)的孤波解求解问题.陆宝群等分别利用待定系数法和函数展开法求得了方程(1)的精确孤波解[8-9];Ito[10]运用循环算子推出了当α=δ=-2,β=-6,ε=0时,耦合方程
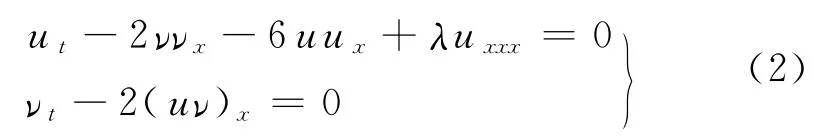
具有无限多的对称性;叶彩儿[11]证明了当α=β=λ=δ=ε=1时,耦合方程
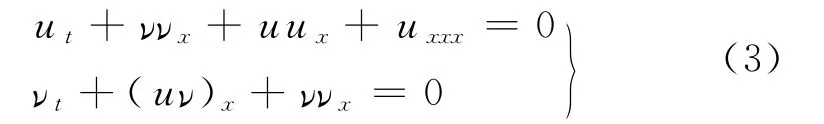
具有Painleve性质,在Painleve性质下可积,并通过自Backlund变换求出了方程(3)的孤立波解和奇异行波解.
然而以往文献没有给出过方程(1)孤波解唯一性的结论,也没有研究过方程(1)的孤波解与周期波解之间的关系.现运用平面动力系统方法研究耦合KdV波动方程(1)的孤波解、周期波解的存在性,给出孤波解唯一性的结论,并分别运用假设待定法和首次积分法求出这两种解的精确解,还进一步研究这两种解的相关性.目前研究非线性发展方程孤波解与周期波解之间相互关系的文献还比较少,这种研究在理论和应用上显然是有意义的,因为它可揭示参数的变化对解的影响,加深人们对非线性波动的认识,并给非线性波动的控制提供有益的信息.
文中首先运用平面动力系统理论和方法对方程(1)的行波解进行定性分析,给出不同参数下的全局相图,说明在一定条件下该方程只存在唯一的钟状孤波解,而同时却有无穷多个周期波解.其次分别运用待定系数法和首次积分法求出该方程钟状孤波解和周期波解的精确表达式,并直观指出它们所对应的解轨线在全局相图中的位置.随后讨论了方程孤波解与Jacobi椭圆函数型周期波解的关系,即当模数k趋近于1时,Jacobi椭圆函数周期波解逐渐扩张演变为钟状孤波解.最后作出了Jacobi椭圆函数周期波解向钟状孤波解演变的三维示意图.
2 方程(1)有界行波解的定性分析
设方程(1)有行波解u(x,t)=u(ξ)=u(x-ct),ν(x,t)=ν(ξ)=ν(x-ct),将其代入方程(1)中,可得
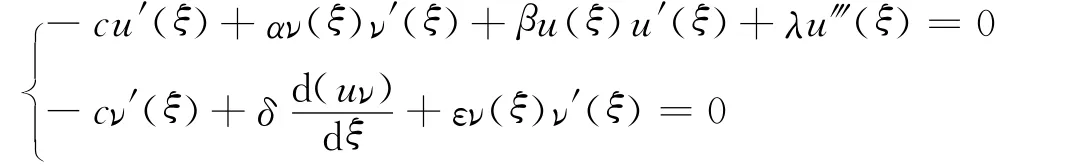
将上式积分一次,可得
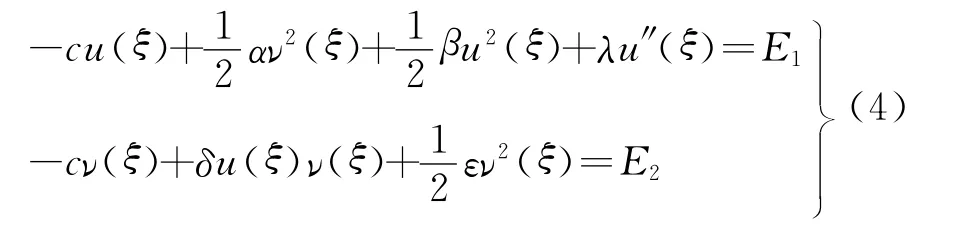
其中,E1,E2为积分常数.由式(4)中第二个式子,可知
为使得u(ξ)处处正则,现取E2=0,这等价于u(ξ),ν(ξ)当的极限满足
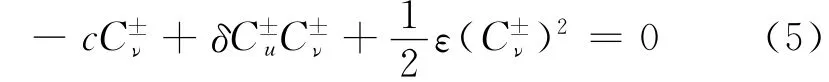
将式(6)代入式(4)中第一个式子,可得
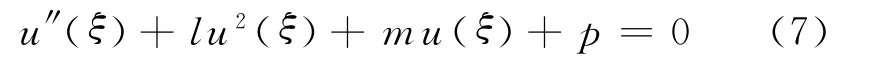
其中
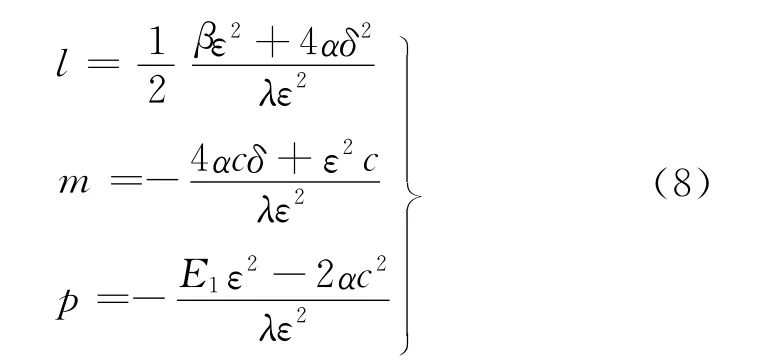
这样,在积分常数E2=0的条件下就将求方程(1)孤波解和周期波解的问题转化为了式(6)和式(7).由于式(6)中u(ξ)满足方程(7),故对方程(7)解的性态和求解的研究是本文的关键.现在研究方程(7),令x=u(ξ),y=u′(ξ),则方程(7)可转化为与之等价的平面动力系统
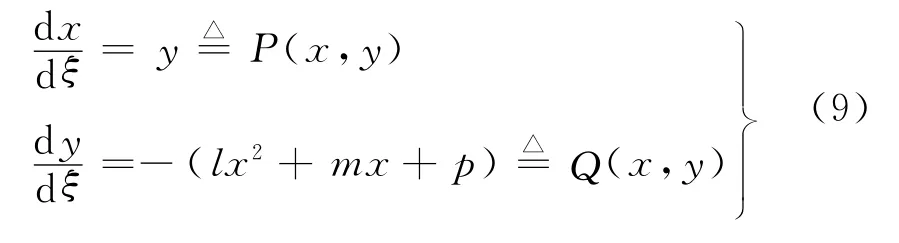
在(x,y)平面上,系统(9)有限远奇点的个数依赖于方程f(x)=lx2+mx+p=0的实根的个数.记f(x)=0的判别式为Δ=m2-4lp.易知该方程在Δ=0时有一个实根,在Δ<0有两个共轭复根,在Δ>0有两个不等的实根.因现只考虑系统(9)的有界行波解,所以始终假设Δ>0.设方程f(x)=0的实根为a1,a2,分别为当l>0时,a1<a2;当l<0时,a1>a2.记系统(9)在奇点Pi(ai,0)(i=1,2)处的Jacobi矩阵为
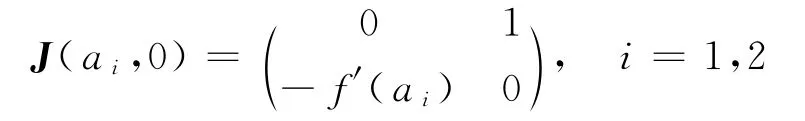
显然,系统(9)是Hamilton系统,有首次积分
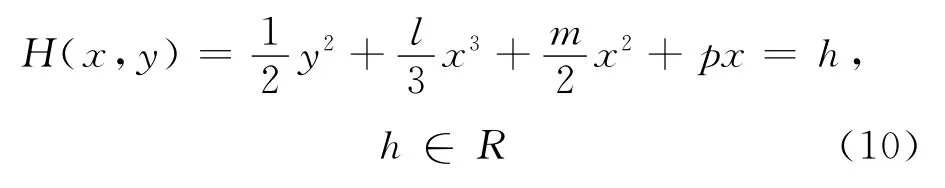
由Liouville定理的推论可知,Hamilton系统不可能存在渐近稳定与不稳定的平衡点(焦点、结点),平衡点只能是中心或鞍点;也不可能存在渐近稳定与不稳定的极限环,只可能存在简单闭轨.在典型的Hamilton系统中,只可能存在有限个平衡点,但可以有无穷多个周期闭轨.
对系统(9)作Poincare变换,可得系统(9)在y轴上各存在一对无穷远奇点Ai(i=1,2),且在Ai周围各存在一个抛物型区域.另外,Poincare圆盘的圆周为轨线.
由上述分析,可得到系统(9)的全局相图,如图1所示.
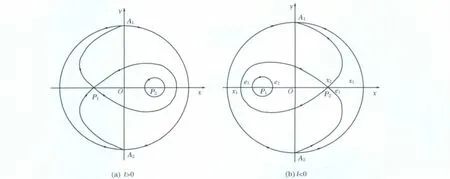
图1 系统(9)的全局相图Fig.1 Global phase portraits of system(9)
由相图1,可得到下列命题.
命题1 设l≠0,除去奇点P1,P2和轨线L(P1,P1)以及由L(P1,P1)包围的闭轨线外,系统(9)的其它轨线均是无界的,并且这些轨线上的点的x坐标值和y坐标值也均是无界的.
证明 设l≠0,除去奇点P1,P2和轨线L(P1,P1),L(P2,P2)以及这些轨线周围的闭轨线外,系统(9)的其它轨线均是无界的,它们在+∞时,或者趋于A1或者趋于A2.因此,这些轨线上的y坐标值一定是无界的.下面用反证法证明这些轨线上的x坐标值也是无界的.设这些轨线上的点的x坐标值是有界的.一方面,由于轨线上的任意点的切线斜率满足
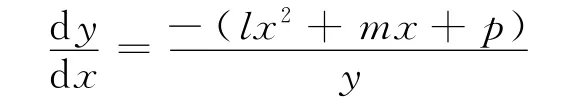
命题2 设l≠0,系统(9)存在一条同宿轨道和无穷多条闭轨线(见图1).
考虑到平面动力系统(9)中的同宿轨对应方程(1)的钟状孤波解,闭轨对应方程(1)周期行波解,因此由命题1、命题2和全局相图1,可得如下定理.
定理1 设积分常数E2=0,若行波波速c和积分常数E1满足m2-4lp>0,则方程(1)存在唯一的钟状孤波解(对应于同宿轨道L(P1,P1))和无穷多个周期行波解.
由于所讨论的方程(1)中参数α,β,λ,δ,ε都是非零的,故命题1和命题2中假设l≠0自然成立.
3 方程(1)的钟状孤波解
受文献[12]的启发,方程(7)有解
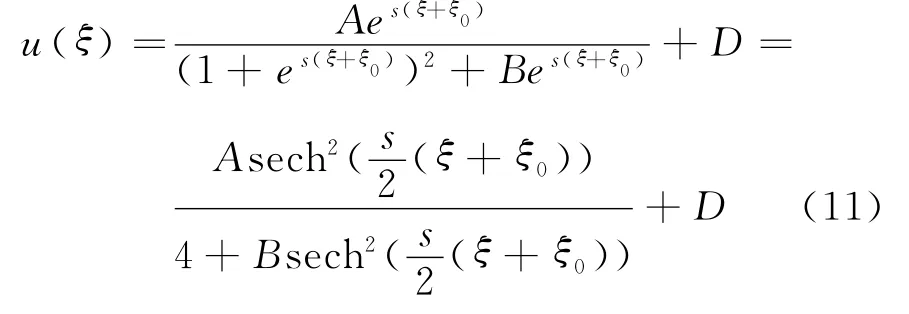
其中,A,B,s,D待定.将式(11)代入方程(7)中,根据es(ξ+ξ0)(s=0,1,2,3,4,5,6)的线性无关性,并经化简得到A,B,s,D满足的方程组
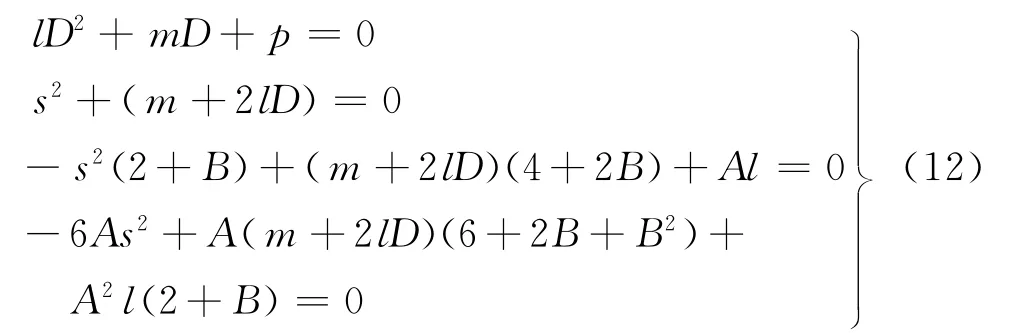
解方程组(12),可得下列两组解
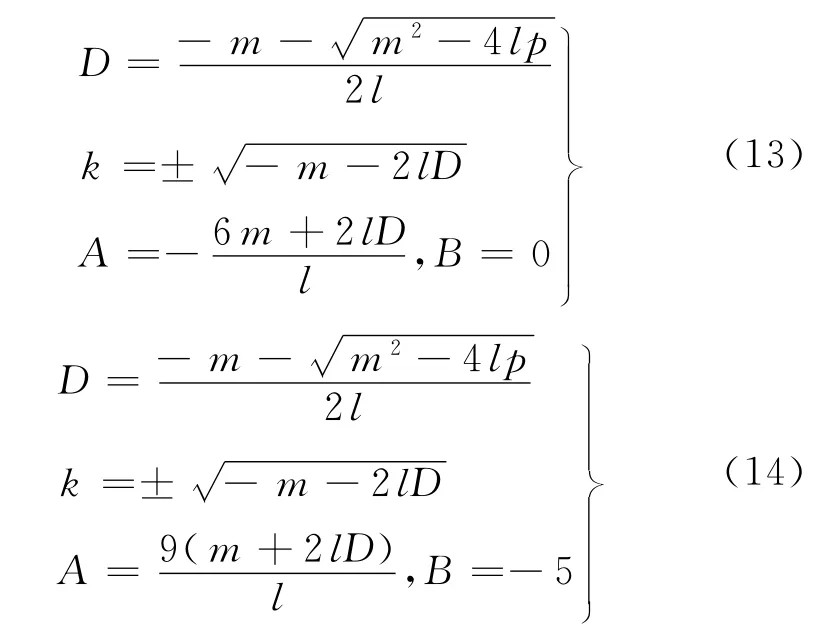
又因将式(14)中各数值代入式(11),可得方程(7)的解为
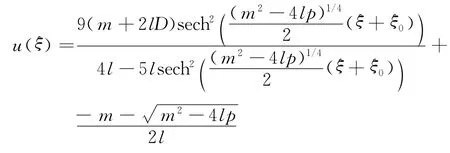
经判定,此解不是有界行波解,故可将其排除.
综合上面计算和前面的定性分析的结果,可得到下面关于方程(1)钟状孤波解的定理.
定理2 假设定理1中条件成立,则方程(1)的唯一钟状孤波解为
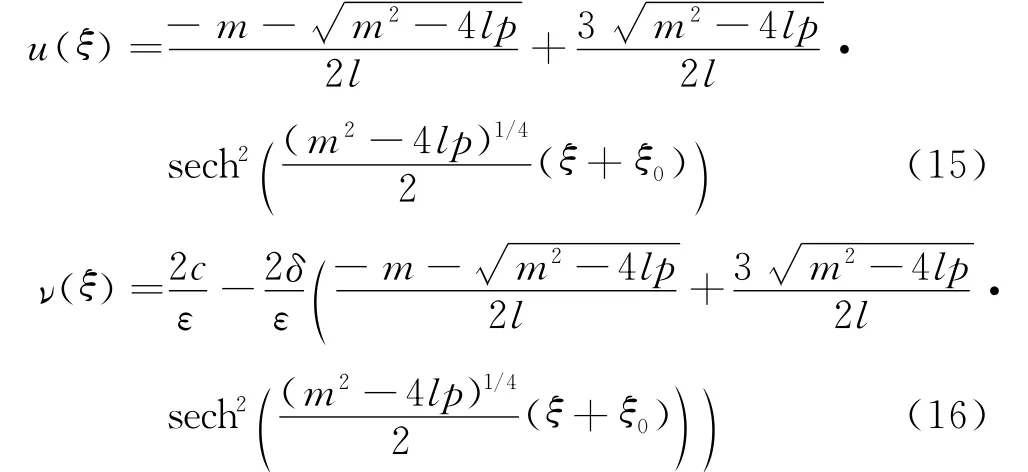
其中,l,m,p由式(8)给定.孤波解(u(ξ),ν(ξ))中的u(ξ)对应于图1中的同宿轨L(P1,P1).
定理2中的唯一性,已由定理1给出.另外因为sechx是偶函数,当时的解与k=时的解相同.
易验,本文所求孤波解与文献[8]用函数展开法所求方程(1)的钟状孤波解是等价的.文献[9]用待定系数法所求钟状孤波解是本文所研究方程(1)的钟状孤波解式(15)和式(16)在m2-4lp=16,E1=E2=0时的情况.文献[10]中通过自Backlund变换求得方程(3)的孤波解是本文研究的方程(1)在α=1,β=1,λ=1,δ=1,ε=1,即l=5/2,m=-5c时的特殊情况.用定性分析及假设待定结合方法的好处在于:利用定性分析的结果,可以清楚地看出方程(1)有界行波解存在的个数和大致形态,可以很直观地指出用假设待定方法求出的方程(1)的有界行波解对应的解轨线在全局相图中的位置,两者之间具有一一对应的关系.
4 方程(1)的周期波解
现结合前面定性分析中的部分结论,通过适当变换并运用首次积分方法对方程(1)的周期波解进行求解.
由对方程(1)有界行波解的定性分析中可知,平面动力系统(9)是Hamilton系统,且具有首次积分式(10),式(10)即为系统(9)的Hamilton函数.以l<0的情形为例,求出对应图1(b)中同宿轨道所围中心的闭轨线对应的周期波解,对于l>0情形的结论可类似得到.
设(a,0)为周期轨道与x轴的交点,由于在对称同宿轨道内包围中心的同一周期轨道上点的Hamilton量相等,即于是,有
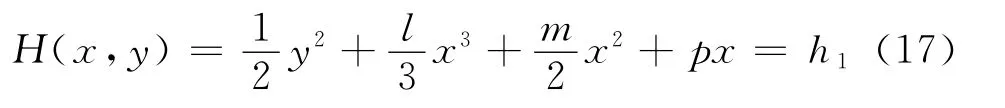
可证得Hamilton量的取值范围为
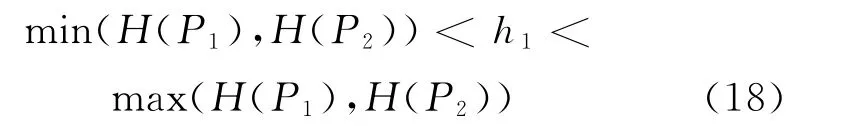
其中
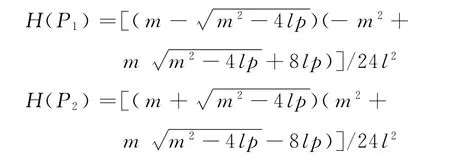
由式(17),可得
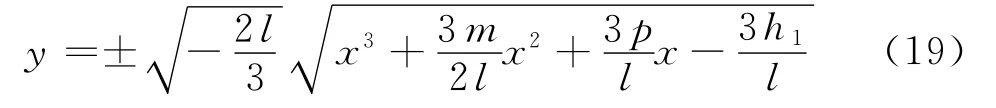
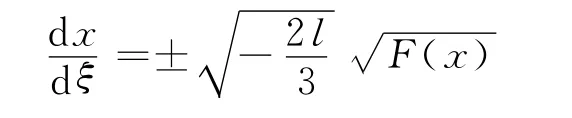
对上式积分一次,可得
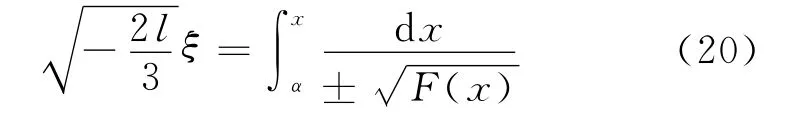
易验,在Δ=m2-4lp>0和h1满足式(17)条件下,F(x)=0有3个实根e1,e2,e3,它们由l,m,p,h1确定,故F(x)可写成F(x)=(x-e1)(x-e2)(x-e3).当l<0时,有e3<a2<e2<a1<e1,且在(e3,e2)及(e1,+∞)时,F(x)>0,此时为求出有界的周期波解,应限制x在(e3,e2)内取值,如图2所示.现取α=e3,并令
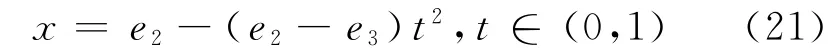
将式(22)代入式(20),可得
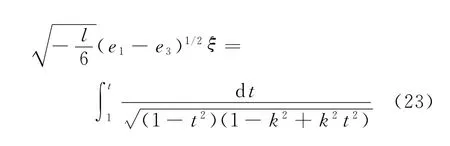
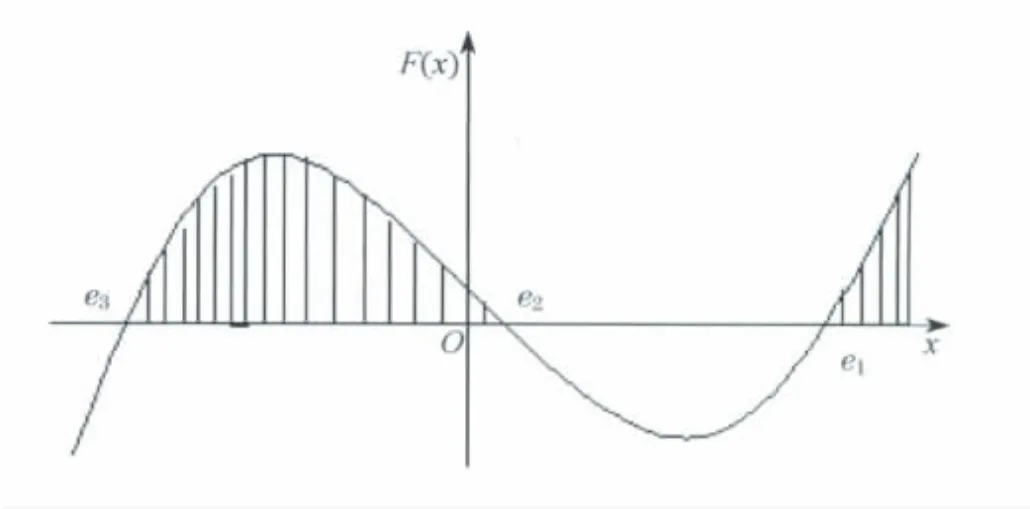
图2 F(x)>0的范围Fig.2 Range of F(x)>0
利用椭圆函数cn(ζ,k)的微分公式
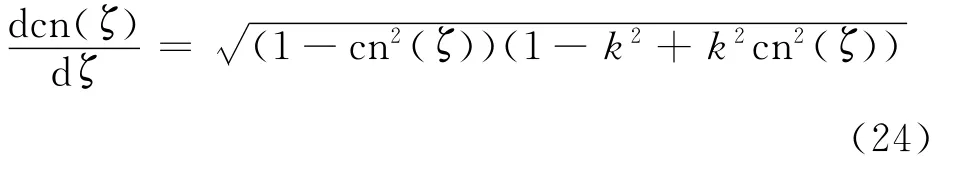
令t=cn(ζ),则式(24)变为
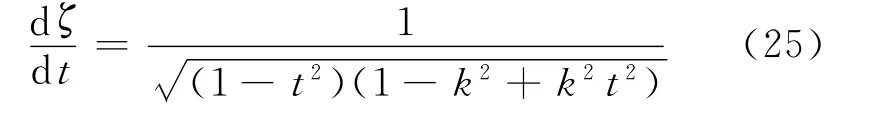
考虑到cn(0)=1,由式(25),有
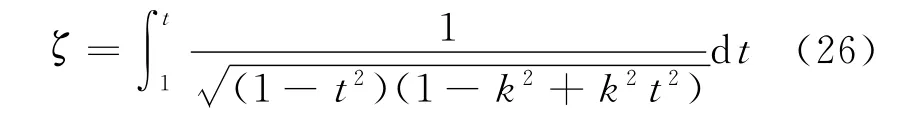
将式(26)代入式(23)中,立即有
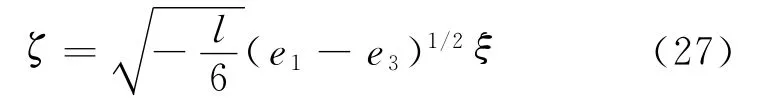
将其代入式(22),得到方程(7)的周期波解
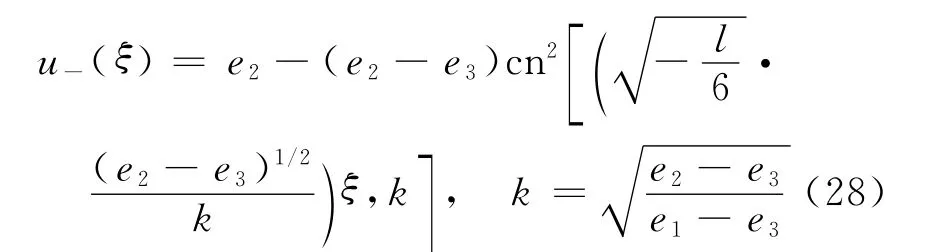
同理,当l>0时,图1(a)中同宿轨道所围中心的闭轨线对应方程(7)的周期波解为
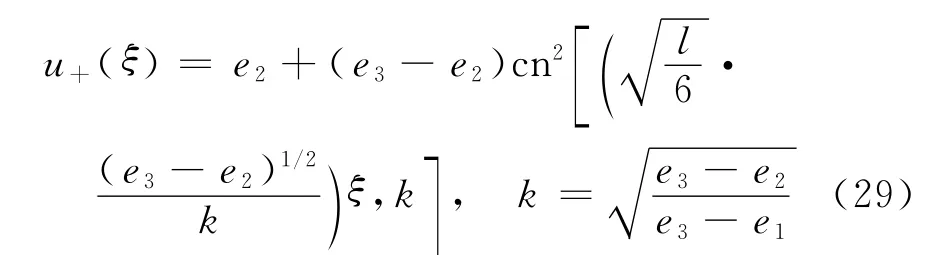
综合上面的计算,可得到关于方程(1)的周期波解的如下定理.
定理3 设定理1中条件成立.则方程(1)有Jacobi椭圆函数周期波解
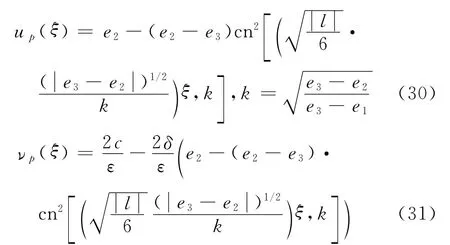
up(ξ)对应于图1(a),(b)中的同宿轨道L(P1,P1)所包围中心奇点的闭轨线.
下面通过假设待定法求方程(7)的周期波解.受文献[13]的启发,假设方程(7)有解
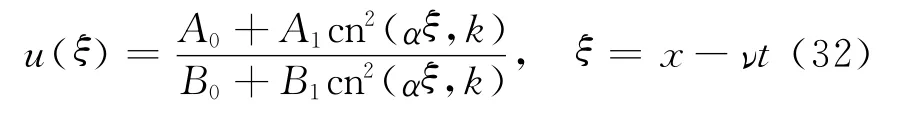
将其代入到式(7)中,可求得
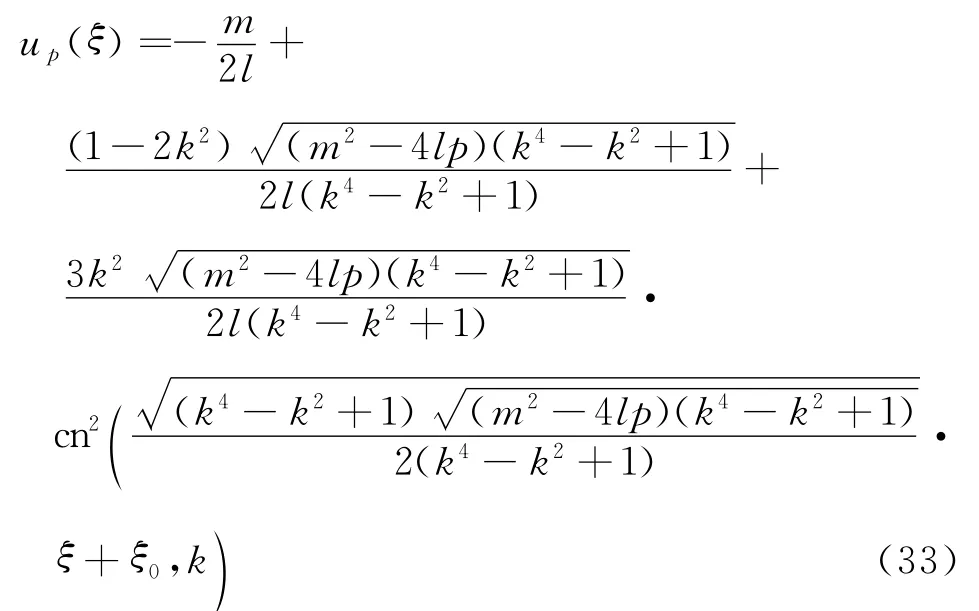
用首次积分法求解方程(1)的周期波解,主要目的在于以此说明椭圆函数中的模数k与周期波解对应的轨线和x轴的交点e1,e2,e3相关,从而k与方程(1)中的参数及波速等相关.
5 方程(1)的孤波解和周期波解的关系
从全局相图的角度观察,方程(1)的孤波解(u(ξ),ν(ξ))中的u(ξ)对应于全局相图1(a),(b)中的同宿轨线L(P1,P1),而周期波解(up(ξ),νp(ξ))中的up(ξ)对应于包围中心的闭轨线,它被包含于由同宿轨线L(P1,P1)所包围的区域中.下面以l<0的情形为例进行讨论.考察在对称同宿轨道内的周期波解up(ξ)当k→1时向孤波解u(ξ)的演变,对于l>0情形的结论可类似得到.
当l<0时,系统(9)过鞍点P1(a1,0)的同宿轨道上点的Hamilton量为其中再由Hamilton函数知,H即
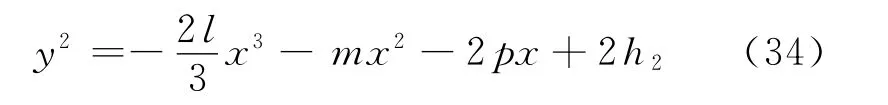
Hamilton量为h2的轨线在l<0时与x轴的交点.其中,包含于同宿轨道的周期闭轨线与x轴的交点的横坐标e1,e2,e3与x1,x2,x3关系为x1<e3<e2<x2=a1<e1<x3(见图1(b)),且当模数时,有e3→x1, e2→x2=a1, e1→x2=a1.
结合上面的分析,可求得
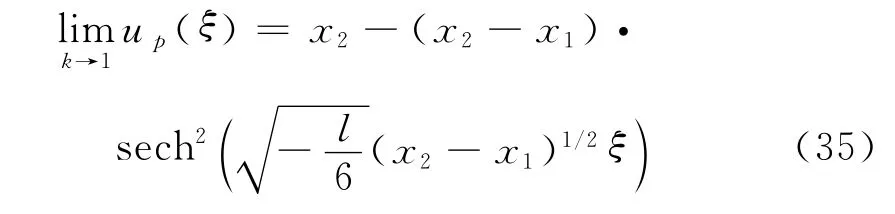
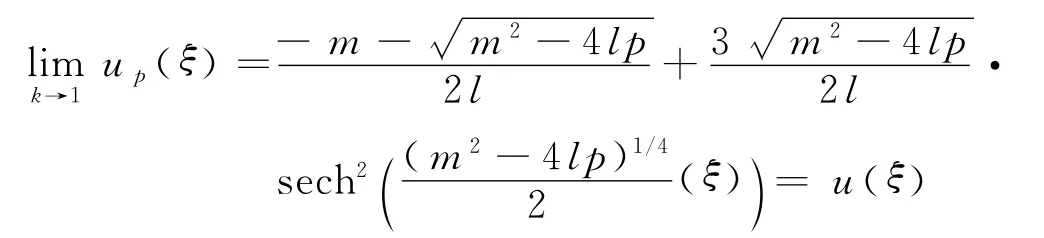
综合上面的计算和前面的定性分析,可得到如下定理.
定理4 当k→1时,方程(1)的周期波解对应相图上的周期闭轨扩张成同宿轨道L(P1,P1).
为了直观地体现周期波解与孤波解之间的关联性,现作出Jacobi椭圆函数周期波解up(ξ)向孤波解u(ξ)演变的三维示意图,如图3所示.图3中,取此时l=3,m=4,p=1.
[1] Kumpershmidt B A.A coupled Korteweg-de Vries equation with dispersion[J].J Phys A:Math Gen,1985,(18):571-573.
[2] Garder C S.The Korteweg-de Vries equation and generalizations IV[J].Journal of Mathematical Physics,1971,12(4):1548-1551.
[3] Konno K,Ichikawa Y H.A modified Korteweg-de Vries equation for ion acoustic waves[J].J Phys Soc Japan, 1974,37(7):1631-1636.
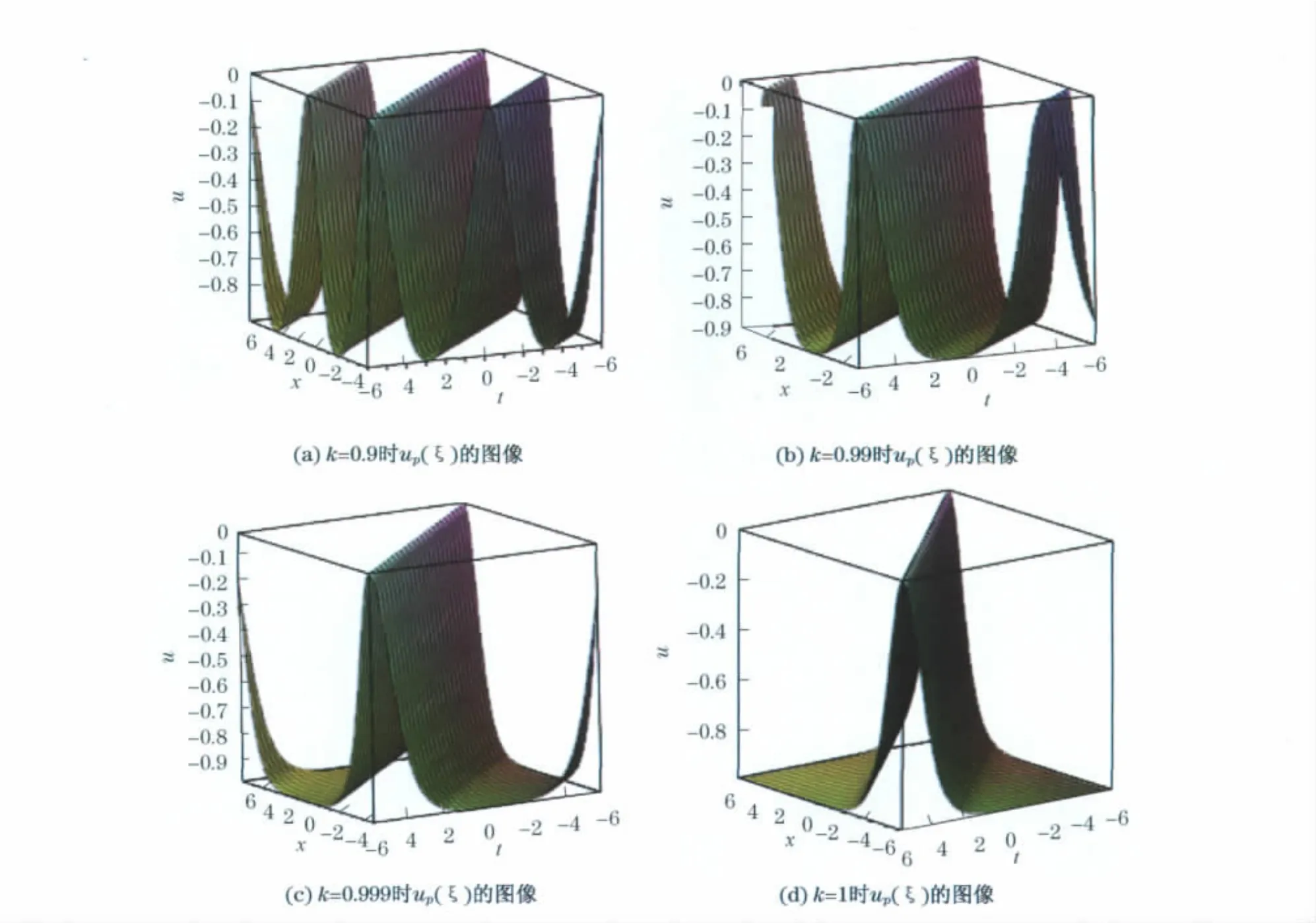
图3 k→1时周期波解up(ξ)趋向于孤波解u(ξ)Fig.3 Periodic wave solution up(ξ)tends to solitary wave solution u(ξ)when k→1
[4] Dodd R K,Eilbeckj C,Gibbon D J,et al.Solitons and nonlinear wave equations[M].London:Academic Press Inc Ltd,1982.
[5] Narayanamurti V,Varma C M.Nonlinear propagation of heat pulses in solids[J].Phys Rev Lett,1970,25(16):1105-1108.
[6] Tappert F D,Varma C M.Asymptotic theory of selftrapping of heat pulses in solids[J].Phys Rev Lett,1970,25(16):1108-1111.
[7] Zhang W G,Chang Q S,Fan E G.Methods of judging shape of solitary wave and solutions formula for some evolution equations with nonlinear terms of high order[J].J Math And Appl,2003,287(1):1-18.
[8] Lu B Q,Pan Z L,Qu B Z,et al.Solitary wave solutions for some systems of coupled nonlinear equations[J].Physics Letters A,1993,180(1):61-64.
[9] Xu X J,Zhang J F.New exact and explicit solitary wave solutions to a class of coupled nonlinear equations[J].Communications in Nonlinear Science &Numerical Simulation,1998,3(3):189-193.
[10] Ito M.Symmetries and conservation laws of a coupled nonlinear wave equation[J].Phys lett A,1982,91(7):335-338.
[11] 叶彩儿.几个非线性发展方程(组)的精确解与Painleve分析[D].杭州:浙江大学,2003:28-31.
[12] 张卫国,刘刚,任迎春.非线性波动方程的孤波解与余弦周期波解[J].上海理工大学学报,2008,30(1):15-21.
[13] An J Y,Zhang W G.Exact periodic solutions to generalized BBM equation and relevant conclusions[J].Acta Mathematicae Applicatae Sinica,2006,22(3):509-516.

