A股市场系统跳跃风险研究

赵久伟， 肖庆宪

（上海理工大学管理学院，上海 200093）

1 问题的提出

在金融经济学中，资本资产定价模型（CAPM）在金融资产定价理论中得到了广泛应用，它构成了投资组合管理和风险管理与决策的基础，在金融衍生产品定价、基金绩效评估等方面也有相关应用.在该模型中β系数是用于衡量不可分散（nondiversifiable）风险的一种指标，或称为对系统风险因子的敏感度，即系统风险.

单因子模型的一般形式为

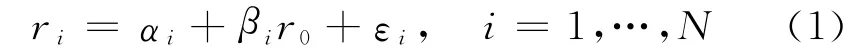
式中，ri为第i项资产的收益率；αi，βi为方程系数；r0为系统风险因子或风险溢差；εi为异质风险（idiosyncratic risk）.单因子模型的一般形式包含了资本资产定价模型，β系数表示单个证券和市场收益的协方差与市场收益方差的比率.长期以来，国外众多学者讨论了对β系数如何进行更精确估计和预测的问题.β系数不能够直接观察得到，而估计β系数的传统方法局限于滚动线性回归（rolling linear regression），且大多采用了信息量有限的低频收益数据［1］.随着信息技术的发展，高频金融数据的获取成本降低，Andersen等［2－3］、Bollerslev等［4］和Barndorff－Nielsen等［5］基于高频数据探讨了对β系数准确估计与预测的重要性，并在此基础上提出了已实现变差（realized variation）测度.他们认为基于高频交易数据估计得到的β系数一般优于传统回归法.由于考虑到股票价格过程中连续变动与跳跃（jump）的区别，Todorov等［6］将系统风险分解为系统扩散风险和系统跳跃风险，并分别给出了两种风险的一致估计量，他们指出两种变动方式产生的风险溢差并不相等.我国部分学者对于β系数的研究还大多局限于稳定性和时变性的讨论，而没有对系统风险和跳跃风险展开研究.闰冀楠等［7］和苏卫东等［8］对中国股市β系数进行了单位根检验，检验其稳定性；刘永涛［9］对上海证券市场β系数的相关特性进行了实证研究；徐占东等［10］和陈学华等［11］利用CusuMSQ统计量来验证β系数的稳定性并建立模型；王春峰等［12］利用已实现波动方法探讨了股本与行业因素对不同模型预测β系数结果的影响；斯叶青等［13］研究了中国股市跳跃行为的发生机制，并描述了跳跃风险对风险管理的影响.目前为止，国内大部分学者还仅局限于β系数时变性和稳定性的讨论，且大多采用信息量有限的低频收益数据，估计方法也存在不可忽略的估计误差.同时，没有区分系统扩散风险（diffusive risk）和跳跃风险（jump risk）的区别，这就给将β值更准确地应用于资产定价和风险管理带来了很大的限制.

在线性因子模型的框架下，根据连续价格过程和非连续价格过程的不同性质，将市场收益率分解为连续收益率和跳跃收益率，根据式（1）得到

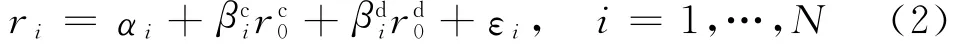
本文将在一般理论框架下利用非参数方法分别估计系统扩散风险和系统跳跃风险，并以上海股票市场为研究对象，选取其中30只股票为样本讨论扩散风险和跳跃风险的特征及其影响.

2 连续时间模型

假设定义在概率空间（Ω，F，（F）t≥0，PP）的股票对数价格pi在时间区间［0，T］上满足以下过程［6］

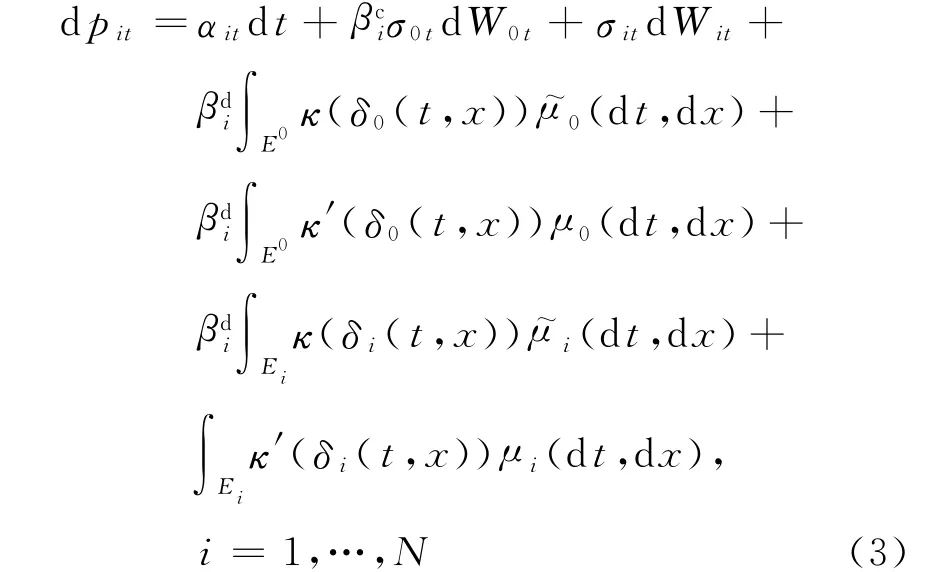
式中，αit为连续的局部有界变差过程；σit，σ0t为随机波动过程；（W0，W1，…，WN）表示N＋1维布朗运动且相互独立；μ0，，μi和均为泊松测度，μi之间相互独立，i＝1，…，N；κ（x）为定义在RR上的连续函数，κ′（x）＝x－κ（x），在0附近有κ（x）≡0；δ0（t，x），δi（t，x）为时间t和x的函数；E0，Ei为辅助空间；和分别表示系统扩散风险和系统跳跃风险.

假设资产价格在时间区间［0，T］上连续记录，那么

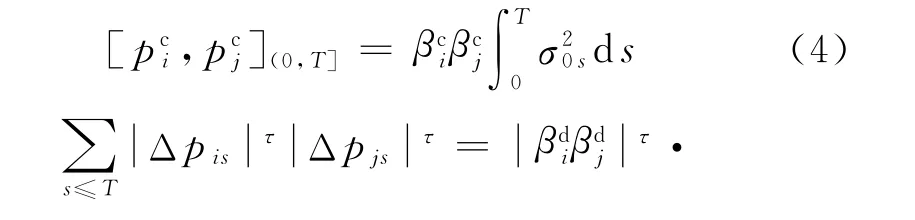
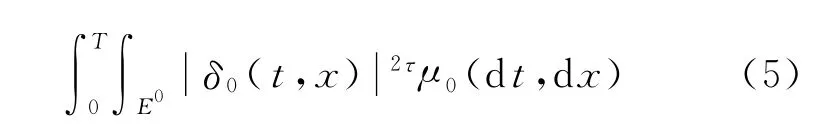
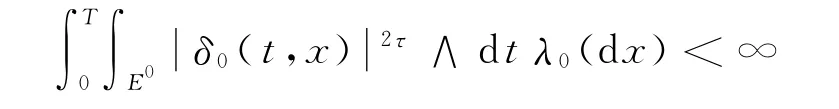
λ0表示泊松分布的期望.通常，τ取1，那么可以表示为非连续二次协变差的绝对值.根据式（5）可以得到β值比率

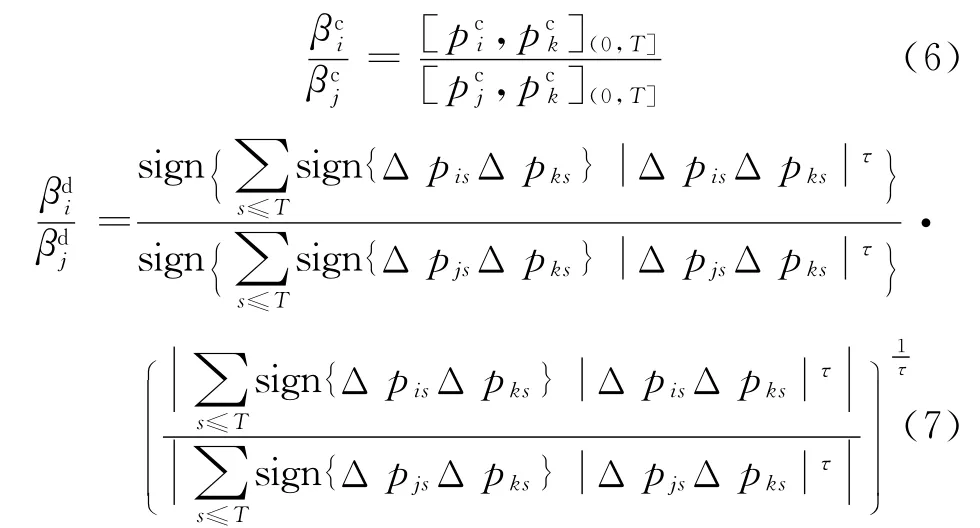
k＝1，…，N，k≠i且k≠j.式（6）和式（7）表示系统风险的相对比率.在资本资产定价模型中，一般假定整个市场的投资组合只暴露于系统风险，系统风险因子通常由市场收益率表示，若市场服从以下过程

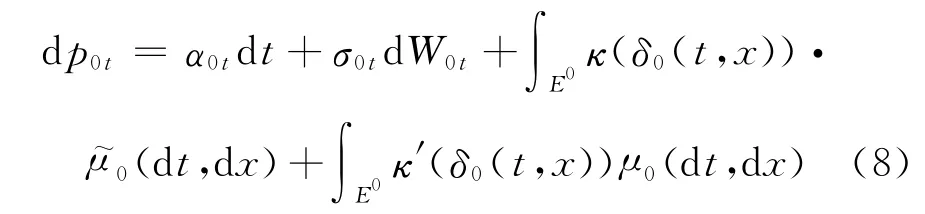
那么式（6）和式（7）可以简化为

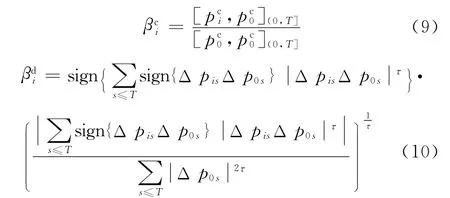
因此，由式（9）和式（10）可以得到单个资产的β系数，而不是β值比率.

3 系统扩散风险和跳跃风险的估计

Todorov和Bollerslev根据Jacod与Todorov［15］的跳跃理论提出了系统跳跃风险的概念，并且基于以下假设条件建立了系统跳跃风险和系统扩散风险的一致估计量.

假设条件：

a.αit，σ0t和σit为右连左极过程，函数δ0（ω，t，x）和δi（ω，t，x）在t时刻可测.

b.当t≤Tk（ω）时，有其中，γk（x）满足为停时序列.δi（ω，t，x）同样适用该条件.

d.σ0和σi为伊藤半鞅，且满足条件a和b.

e.当t≤Tk（ω）时，有

其中，γk（x）满足∫E0（｜γk（x）｜s∧1）·λ0（dx）＜∞，s∈［0，2］，Tk为停时序列.δi（ω，t，x）同样适用该条件.

3.1 系统跳跃风险估计量

在实践中，只能以离散方式记录价格过程，假设lΔn为时间区间［0，T］的时间间隔，l＝0，1，…，［T／Δn］，对数价格向量p＝（p0，p1，…，pN），那么价格增量可以表示为

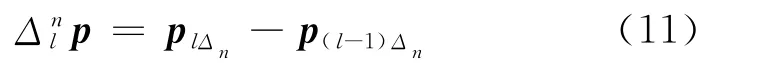
定义函数Vn（φ）t和V′n（φ，α，ῶ）t为

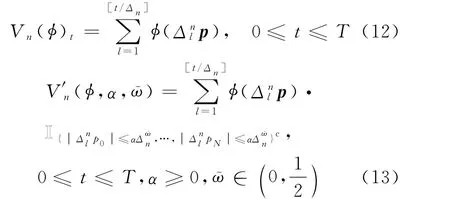
定义f为RRN＋1×RRN＋1的可测函数，f＝

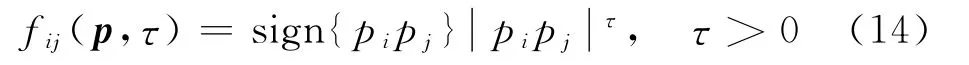
其中，i，j＝0，1，…，N，因为τ为常数，可以用fij（p）表示fij（p，τ）.

那么，跳跃β系数比率的估计量可以表示为

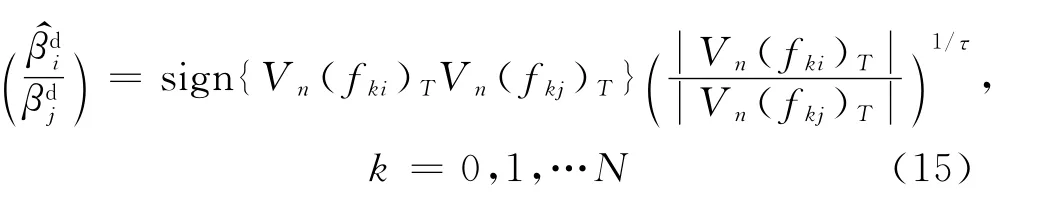
为了使式（15）有意义，必须限制i≠j、i≠k，j＝k当且仅当j＝k＝0.若j＝k＝0，则式（15）可以直接估计

由式（13）可以得到与式（15）渐进等价的估计量

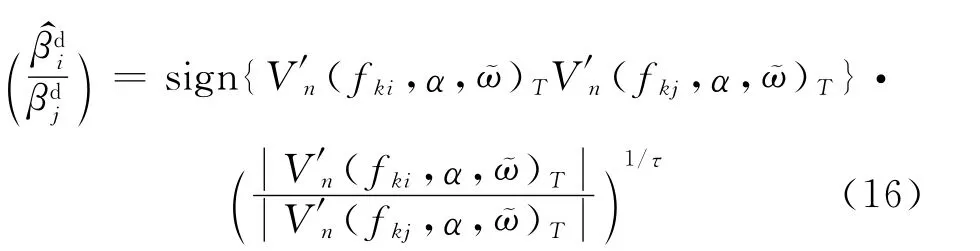
定理1 假设pi和p0分别服从式（3）和式（8），若假设条件a～d成立，则当Δn→0，τ≥2且i≠0时，有：

基于信息集FT，L为概率分布，具体性质和特点见文献［6］，L的条件均值和条件方差分别为E（L｜F）＝0，Var（L｜FT）＝VT.若对所有时刻Sq≤T，有Δp0SqΔσiSq≡0，则L服从正态分布.

d.若假设条件e成立且s＜2，则当j＝k＝0时，渐进方差VT的估计值可以由一致估计量给出.

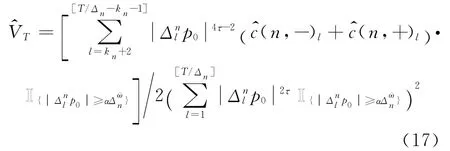
3.2 系统扩散风险估计量

X表示N维半鞅，定义N维已实现变差为

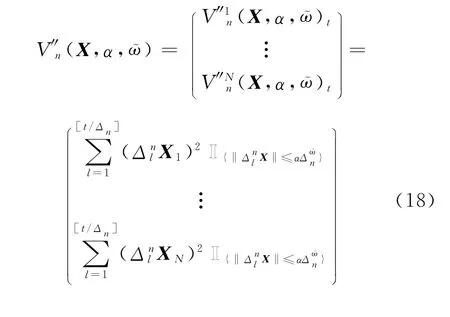
定义价格向量

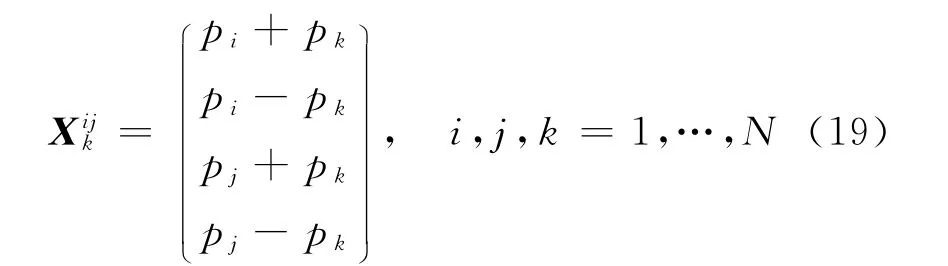
于是，系统扩散风险比率的估计值可以表示为

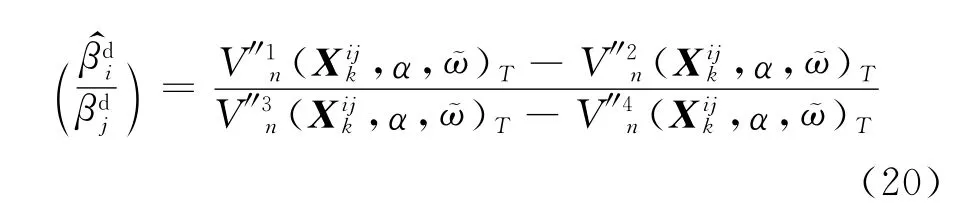
其中，i≠j、i≠k，j＝k当且仅当j＝k＝0.

对于系统扩散风险的渐进分布性质，Todorov和Bollerslev给出了下面的定理.

定理2 假设pi和p0分别服从式（3）和式（7），若假设条件a～e成立则当Δn→0时，有：

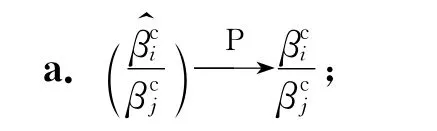
c.方差KT的一致估计量为

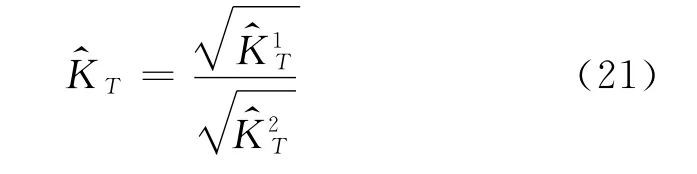
其中

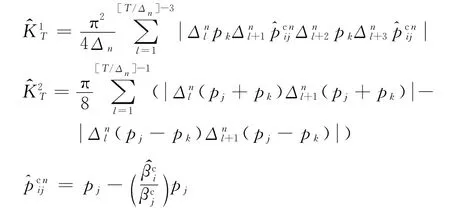
4 实证分析

本文选取2004年1月2日至2008年12月31日5年中上证综合指数和沪市有代表性的30只股票5min数据作为高频数据采样进行研究，数据来自于万得（WIND）金融数据库（www.wind.com. cn）.在实践中，一般选择市场组合作为系统风险因子，因此将上证综合指数作为市场组合分别估计个股的系统扩散风险和跳跃风险.本文剔除了数据不完整的交易日后，总共得到1 212天，60个月，20个季度的交易数据.

由定理1可知，当市场发生跳跃时才能得到个股相对于市场的系统跳跃风险估计量.那么，首先要对市场跳跃行为作出判断.根据Barndorff－Nielsen和Shephard［16］提出的调整对数线性跳跃统计量ZTP，lm，t，在显著水平0.5%下计算得出，上证指数在这1 212天中有127天发生跳跃，60个月中有30个月发生了跳跃，20个季度中有14个季度发生了跳跃.

分别利用式（17）和式（21）计算个股相对市场的系统跳跃风险和系统扩散风险.其中，取j＝k＝0， τ＝2.取＝0.49是为了排除跳跃的无限变差（in－finite variation）.对于取α的值为是为了过滤连续的价格变动，BV表示二次变差；对于取α的值为是为了过滤非连续的价格变动.图1与图2（见下页）分别呈现了中信证券（600030）和三一重工（600031）系统扩散风险βc和系统跳跃风险βd的时间序列图.从图中可以看到，月β系数显得更稳定，变化幅度相对较小；季度β系数变化具有一定的动态依赖性，但是样本采样周期过长，数据量较少；相比之下，由于日β系数受到的“噪音”干扰较大，很难从图中分析日β系数的复杂变化规律.因此，主要集中讨论分析月β系数的性质.

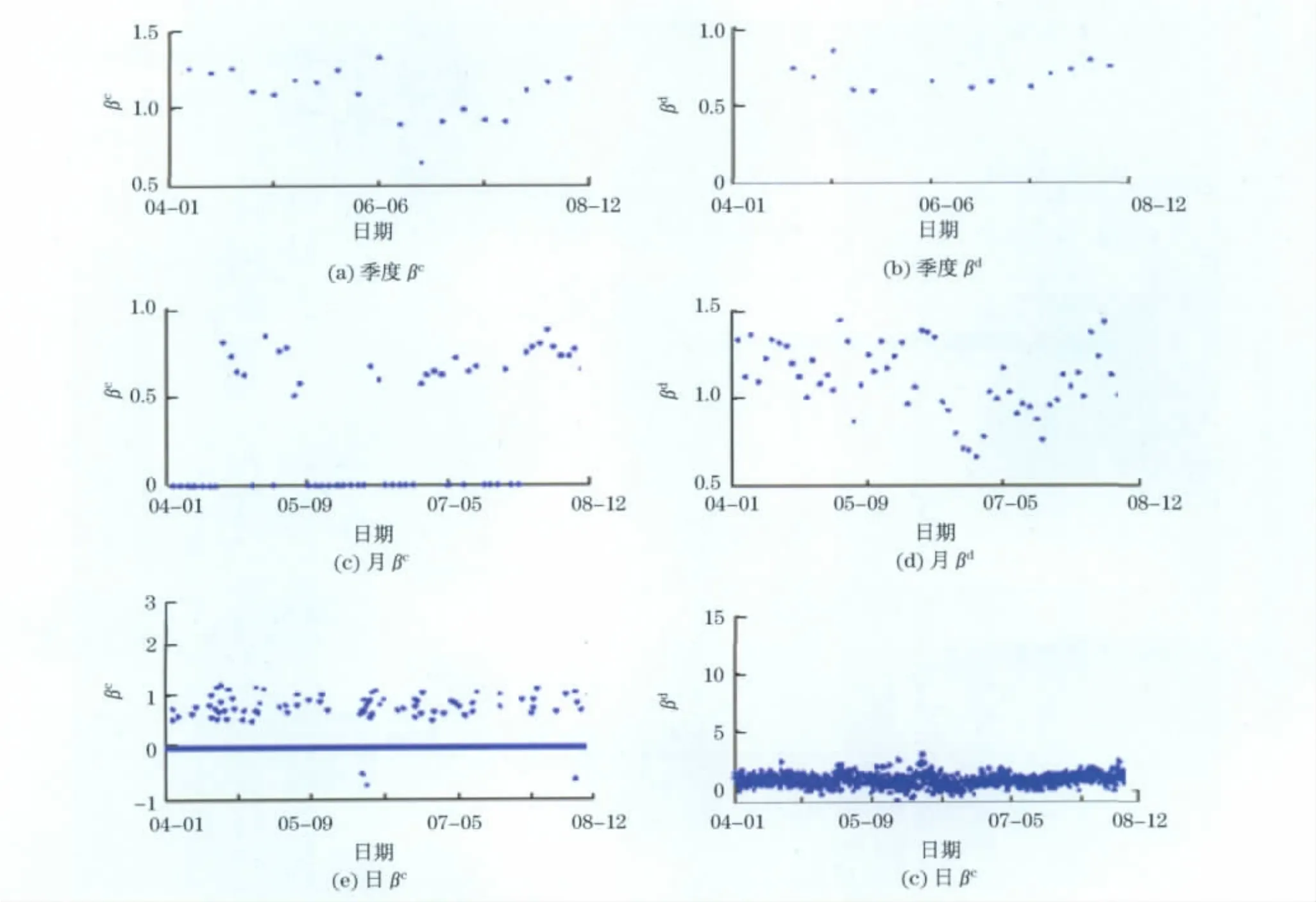
图1 中信证券连续β系数和跳跃β系数时间序列图Fig.1 Time series of quarterly，monthly and daily continuous betas and jump betas for 600030

为了直观地对比系统扩散风险βc和系统跳跃风险βd的区别，将两种指标合并在一张图中，如图3（见下页）所示.从图中可以发现，中信证券的扩散风险与跳跃风险系数截然不同，月βc一般要大于月βd，然而，三一重工的两种风险系数指标相对来说更接近.根据定理1和定理2的渐进分布理论，可以分别计算出风险系数估计量的置信区间.图4（见下页）分别呈现了以一个月为周期的系统扩散风险估计量和系统跳跃风险估计量的置信水平为95%的置信区间.从图4可以看出，中信证券系统扩散风险的置信区间和系统跳跃风险的置信区间基本上没有重叠，这说明，扩散风险和系统风险的确存在差异.但是，三一重工系统扩散风险的置信区间和系统跳跃风险的重叠部分较多，很难从统计的角度说明两者存在差异.此外，还可以从图中观察到一个明显的特征，跳跃风险的置信区间的长度变化幅度较大，而扩散风险的置信区间的长度变化幅度较小，从总体上看相对稳定.

图2 三一重工连续β系数和跳跃β系数时间序列图Fig.2 Time series of quarterly，monthly and daily continuous betas and jump betas for 600031

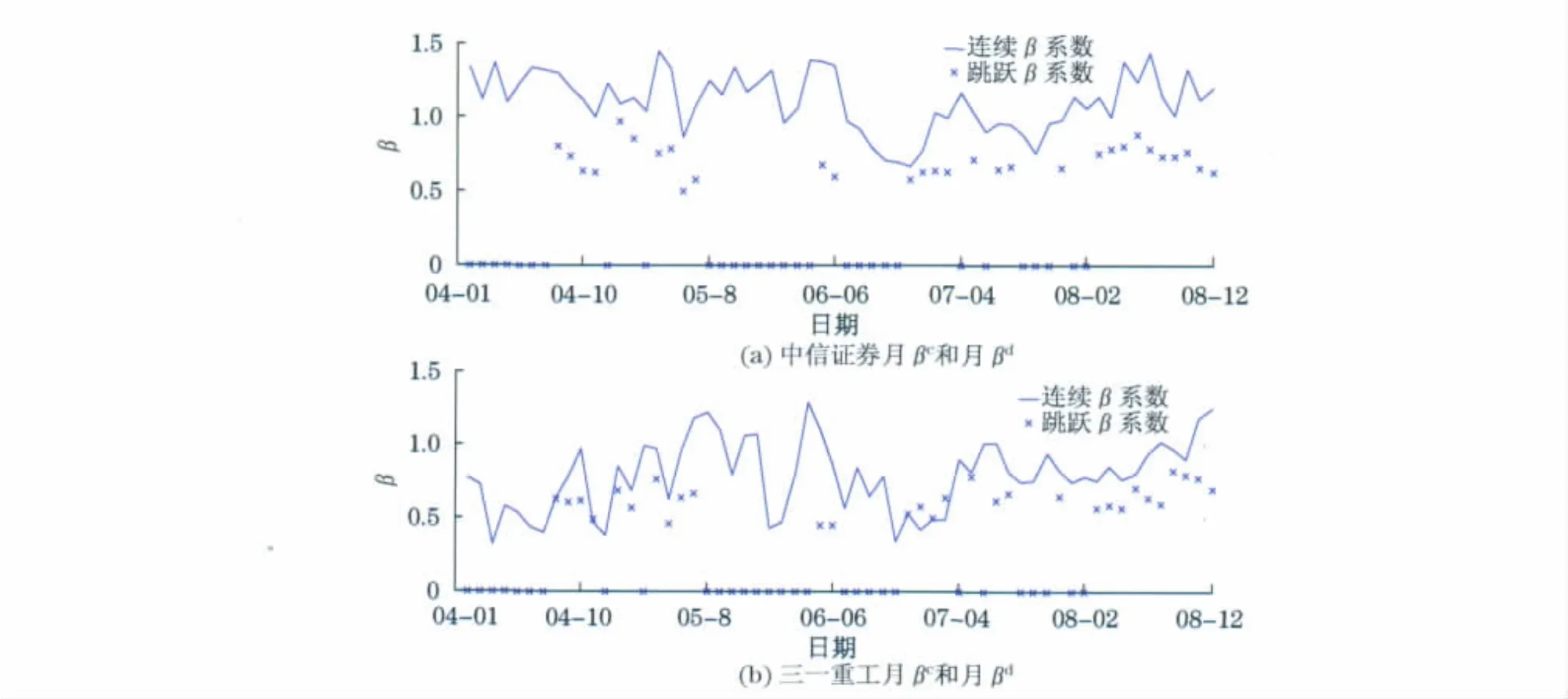
图3 中信证券和三一重工连续β系数和跳跃β系数对比图Fig.3 Monthly betas for 600030and 600031

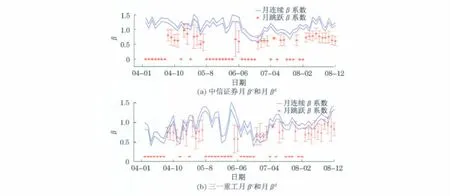
图4 中信证券和三一重工月连续β系数和月跳跃β系数置信区间对比图Fig.4 The 95%confidence intervals of monthly betas for 600030and 600031

为获得两种β系数的差异比较，接下来进行均值之间的对比.本文选取了上证A股市场30只股票为样本，分别计算月βc和月βd并求其均值和均值的置信水平为95%的置信区间，结果在表1中列出.虽然在图4显示出三一重工的置信区间存在较多的重叠部分，但是结果表明其均值的置信区间没有重叠.表1中只有同仁堂和贵州茅台的系统跳跃风险平均值大于系统扩散风险平均值，其余个股的系统扩散风险值更大.其中差异最大的个股是中国石化，差值为0.444 3；差异最小的个股为贵州茅台，差值为0.032 1.而且，除了贵州茅台的置信区间有重叠之外，其它29只股票的置信区间均没有重叠.因此，可以判断个股相对于市场组合的连续变动过程和跳跃变动过程的反应存在明显差异.此外，大盘蓝筹股的系统扩散风险系数较大，更接近于1，例如中信证券、中国石化等.

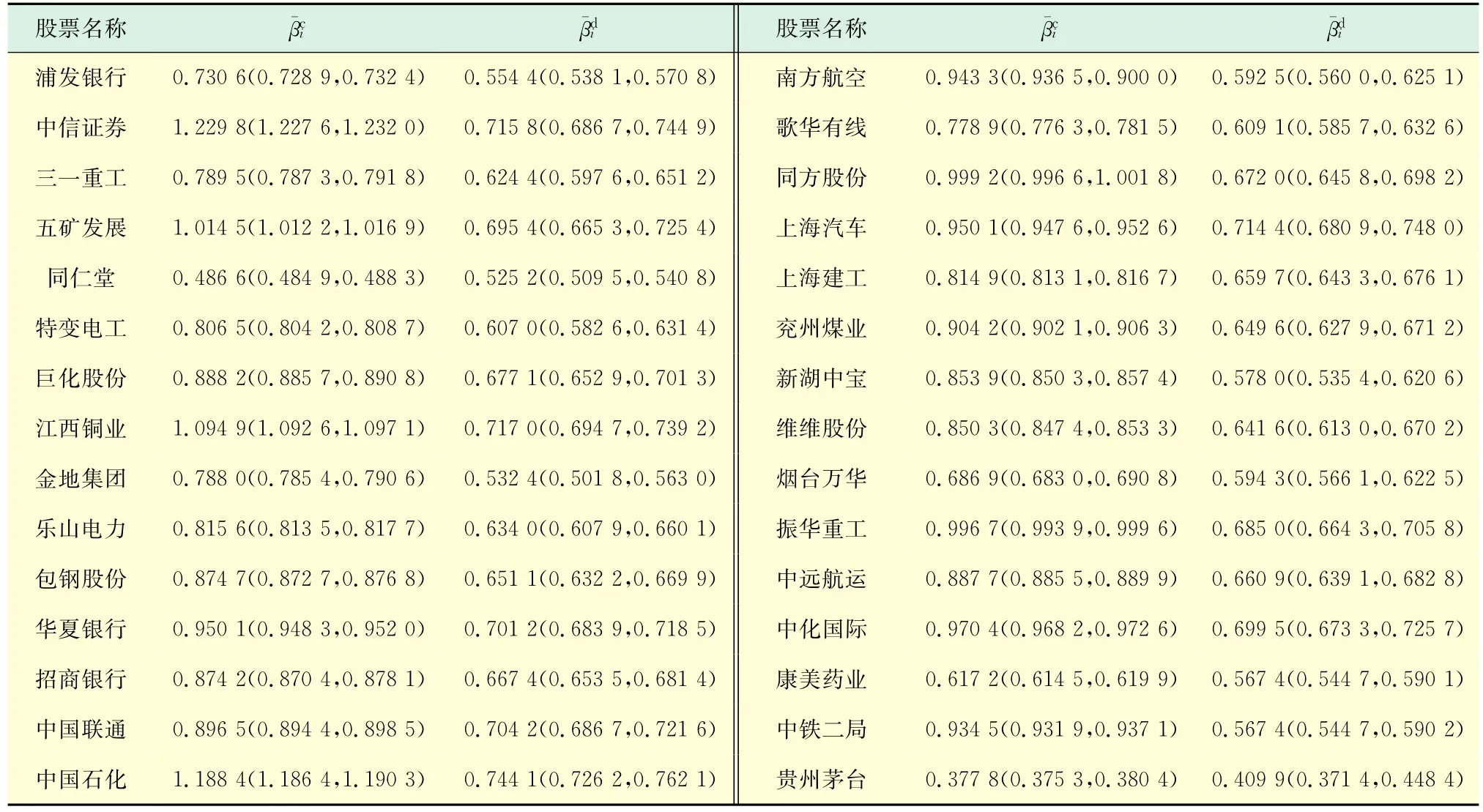
表1 平均月β系数及其置信区间的计算结果Tab.1 Average monthly betas and 95%confidence intervals for thirty stocks

5 结 论

鉴于资本资产定价模型在金融经济学中应用广泛，本文从全新的角度利用非参数估计方法估计了上海股票市场的系统扩散风险和系统跳跃风险，并对其中30只股票的月βc和月βd进行了统计分析.实证研究结果表明：第一，扩散变化所产生的扩散风险与跳跃行为产生的跳跃风险不仅在风险溢价上不同，在性质上也存在着本质的区别；第二，上证A股相对于上证指数的价格连续过程和价格跳跃过程的反应程度不同，即个股的系统扩散风险系数βc和系统跳跃风险系数βd存在明显差异；第三，上海A股市场个股的系统扩散β系数一般要大于系统跳跃β系数，大市值个股的系统扩散β系数更接近1，有的甚至大于1.在实践中，扩散风险一般可以通过连续的交易进行对冲，然而跳跃风险属于突发性事件，冲击力大，往往会使得投资者完全丧失对冲风险的可能性，从而无法避免财富遭受重大的损失，所以跳跃风险不可忽视.因此，股票价格过程的跳跃行为扮演着至关重要的角色，在投资组合建模和风险管理中，有必要考虑整个系统风险及其系统跳跃风险，这无论对于理论还是实践都有着非常重要的意义.

［1］ Fama E，French K.The cross－section of expected stock returns［J］.Journal of Finance，1992，47（2）：427－465.

［2］ Andersen T G，Bollerslev T，Diebold F X，et al.A framework for exploring the macroeconomic determinants of systematic risk［J］.American Economic Review，2005，95（2）：398－404.

［3］ Andersen T G，Bollerslev T，Diebold F X，et al.Realized beta：persistence and predictability［J］.Advances in Econometrics，2005，20（2）：1－39.

［4］ Bollerslev T，Zhang B.Measuring and modeling systematic risk in factor pricing models using highfrequency data［J］.Journal of Empirical Finance，2003，10（5）：533－558.

［5］ Barndorff－Nielsen O，Shephard N.Power and bipower variation with stochastic volatility and jumps［J］.Journal of Financial Econometrics，2004，2（1）：1－37.

［6］ Todorov V，Bollerslev T.Jumps and betas：a new framework for disentangling and estimating systematic risks［J］.Journal of Econometrics，2010，157（2）：220－235.

［7］ 闰冀楠，张维，孙浩.利用MLPOM对上海股市时变CAPM的实证研究［J］.预测，1998，17（2）：60－62.

［8］ 苏卫东，张世英.上海股市β系数的稳定性检验［J］.预测，2002，21（2）：44－46.

［9］ 刘永涛.上海证券市场日系数相关特性的实证研究［J］.管理科学，2004，17（1）：29－35.

［10］ 徐占东，郭多柞.中国股票市场β稳定性分析［J］.统计与信息论坛，2004，19（6）：39－42.

［11］ 陈学华，韩兆洲.中国股票市场行业β系数的时变性［J］.系统工程，2006，24（2）：62－67.

［12］ 王春峰，张亚楠，房振明，等.中国股市已实现β系数的特征分析与建模研究［J］.北京理工大学学报（社会科学版），2008，10（1）：54－58.

［13］ 斯叶青，李能.股票市场收益跳跃性风险研究［J］.全球经济展望，2010，25（4）：43－50.

［14］ Ang A，Chen J.Asymmetric correlations of equity portfolios［J］.Journal of Financial Economics，2002，63（3）：443－494.

［15］ Jacod J，Todorov V.Testing for common arrivals of jumps for discretely observed multidimensional processes［J］.Annals of Statistics，2009，37（4）：1792－1838.

［16］ Barndorff－Nielsen O，Shephard N.Econometrics of testing for jumps in financial economics using bipower variation［J］.Journal of Financial Econometrics，2006，4（1）：1－30.