基于遗传算法的列车空调冷凝器优化设计
陈家星, 余 敏, 姚俊豪
(1.上海理工大学能源与动力工程学院,上海 200093;2.上海法维莱交通车辆设备有限公司,上海 201906)
冷凝器作为列车空调系统的重要组成部分,占据了系统很大的重量和体积,翅片管式冷凝器具有结构紧凑、效率高等优点,在列车空调系统中得到广泛的应用.随着列车运行速度的提升,对空调系统性能的要求也不断提高.在满足基本换热性能和阻力要求的同时,通过优化设计进一步减小冷凝器的重量(或体积),可以减少原材料的消耗,降低牵引功率,有利于提高列车运行速度,达到节能和环保的要求[1].
遗传算法(genetic algorithm,GA)是一种通过模拟自然进化过程搜索最优解的方法.由于该算法对所要求解的优化问题没有过多的限制,且具有高度并行、随机、全局搜索以及自适应的特点,使其在函数优化领域得到越来越广泛的应用.
本文综合分析列车空调冷凝器的热力参数、几何参数以及制冷系统中有关量之间的制约关系,以冷凝器的重量(或体积)为目标函数,引入MATLAB遗传算法工具箱进行优化设计,有效地减少了冷凝器的重量(或体积),为其他类型换热器的优化设计提供了参考.
1 模型建立
在列车空调系统中,受应用条件的限制,一般采用风冷式冷凝器,该冷凝器通常采用几根并联的外套翅片的蛇形管形成长方体管箱.风冷式冷凝器工作时,制冷剂蒸汽在管内冷凝,在轴流式风机作用下,空气在蛇管外横向流动,从而将热量带走.翅片管结构模型如图1所示.图1中,S1为铜管水平间距,S2为铜管竖直间距,Sf为翅片间距,δf为翅片厚度,db为铜管外径,di为铜管内径.
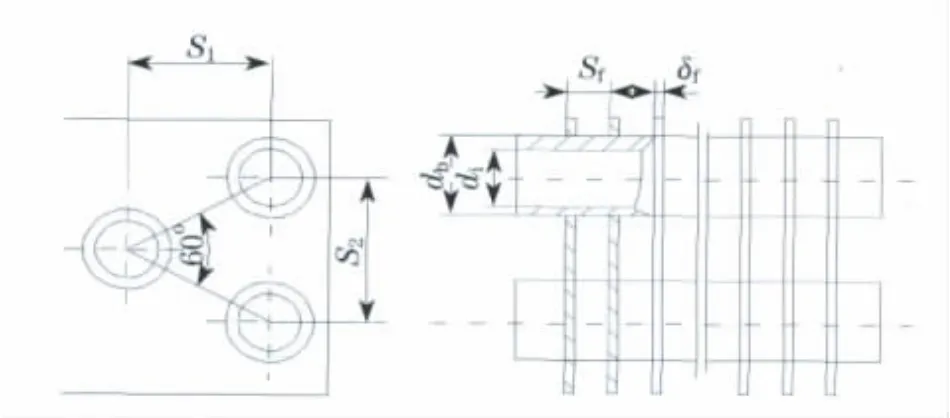
图1 翅片管结构简图Fig.1 Figuration of finned tube heat exchange
现分别以翅片管式冷凝器的重量最轻和体积最小为优化目标.由于冷凝器的重量是结构和几何尺寸的直接函数,而具体结构和尺寸又与装置运行参数、循环工质的热力性质及传热和阻力特性等因素相关.同时,芯体作为冷凝器的核心部件,占有大部分体积和重量.封头、接管等附件只起封闭和连接等辅助作用,因此,只考虑对冷凝器芯体部分进行设计与优化[2].故下文提到重量或体积,如无特别说明,均指冷凝器芯体部分.
为对冷凝器建模,作如下简化处理:忽略各流道相互之间的传热,不考虑分液不均匀问题;管内制冷剂流动简化为一维流动,且不考虑压降,忽略其势能;管外空气的流动视为一维流动;管壁热阻忽略不计.
a.传热量的计算
传热量的计算可由以下传热基本方程式求得[3]
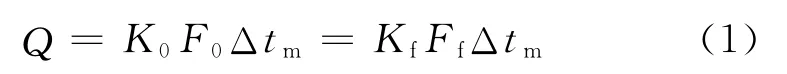
式中,Q为传热量;F0,Ff分别为翅片管外表面积、翅片管光管外表面积;K0,Kf分别对应于以翅片管外表面积、翅片管光管外表面积为基准的传热系数;Δtm为对数平均温差.
b.空气侧表面传热系数的计算
空气侧表面传热系数[4-5]
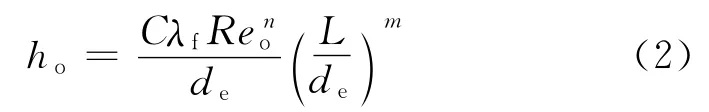
式中,λo为空气导热率;Reo为空气侧雷诺数;L为沿气流方向的翅片长度;de为当量直径.
其中
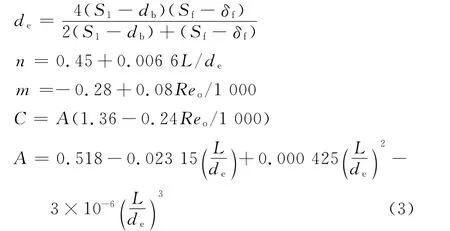
对于叉排管簇,由于气流的扰动比顺排管簇大,故按式(2)计算的表面传热系数还要增加10%.
c.制冷剂侧换热系数的计算
单相区(过冷、过热区)的表面传热系数hi,由Dittus-Boeler换热关联式计算,即
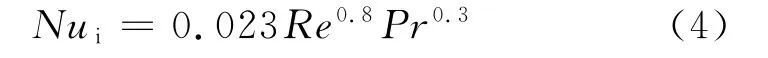
式中,Nui,Re和Pr分别为制冷剂侧流体的努塞尔数、雷诺数和普朗特数.其中
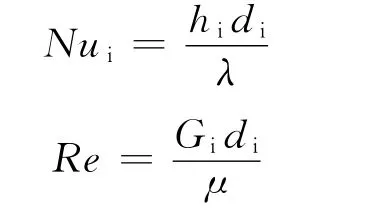
式中,λ为流体导热系数;Gi为流体质量流速;μ为流体运动黏度.
两相区的表面传热系数hi,采用Shah关联式
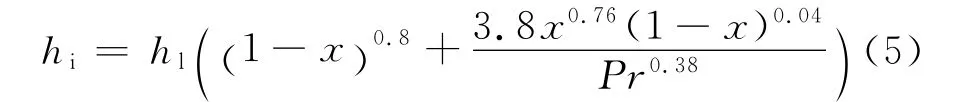
式中,hl为单相区表面传热系数;x为两相区干度.
d.翅片效率
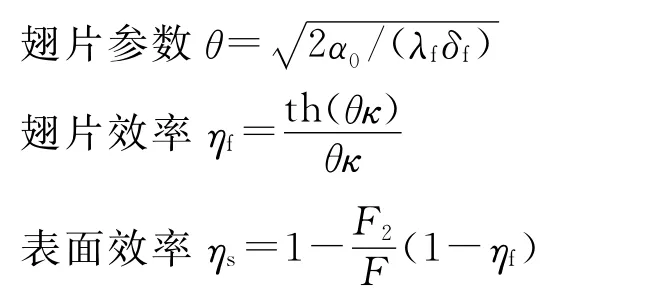
式中,λf为翅片材料导热系数;F2为翅片面积;F为每米翅片总面积;κ为翅片当量高度.
由计算式(2)~式(5)可看出,冷凝器的结构参数影响了空气侧和制冷剂侧换热系数等热力参数,这些热力参数又对换热效率产生影响,进而影响换热器的体积和重量,即冷凝器热力参数、几何参数以及换热效率等相关量之间存在着制约关系.冷凝器的优化设计,要求在满足换热性能的条件下,对管径、翅片间距等要素进行匹配,实现在某个优化目标(如重量最轻、体积最小等)下的最佳组合,而寻找这种最佳组合,与生物进化过程比较类似,因此在冷凝器的优化设计中采用遗传算法是合理、可行的[6].
2 遗传算法在冷凝器优化设计中的应用
2.1 遗传算法原理
遗传算法将每个可能的解看成种群P(t)(t代表遗传代数,也即计算中的迭代次数)中的一个个体,根据预定的目标函数对每个个体进行评价后给出一个适应度值.利用选择、交叉和变异3种遗传算子对初始产生的个体进行组织,产生新的个体C(t).从父代种群和子代种群中选择优秀个体形成新的种群.在若干代后,算法收敛到一个最优个体,该个体很有可能代表遗传算法的最优或次优解.遗传算法的流程如图2所示[7].
2.2 变量的编码
翅片管是冷凝器的基本元件(见图1),换热过程主要依靠翅片管完成,翅片的类型及尺寸是影响冷凝器性能的主要因素,因此选取翅片间距和翅片厚度为优化变量,参考文献[4]选取翅片间距Sf优化范围为1.5~3.0mm,翅片厚度δf优化范围为0.1~0.2mm.考虑到加工、测量精度和计算机运算能力,遗传算法的计算结果保留2位小数.选取的遗传算法主要参数:个体数目为40;变量维数为2;代沟为0.9;最大遗传代数为250;每个种群的长度为20.
2.3 目标函数的确定
取翅片间距和翅片厚度为优化变量,即X=[X1,X2]T=[Sf,δf]T,其中,目标函数为重量W最轻时的表达式为
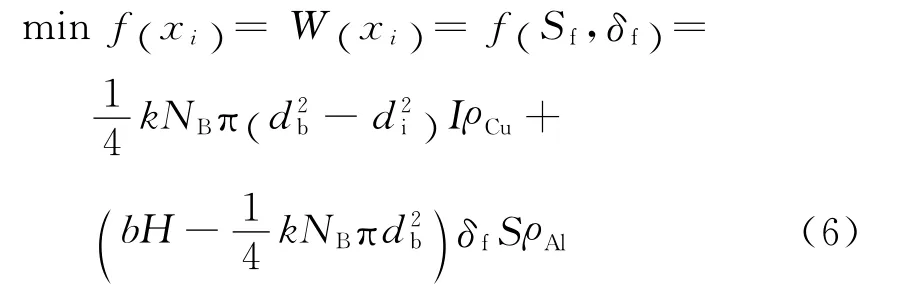
式中,NB为每排管数;k为沿空气流动方向的紫铜管的管排数;I,b,H分别为冷凝器的长度、宽度、高度;S为铝片的片数;ρCu为紫铜的密度,ρAl为铝片的密度.
限制条件为
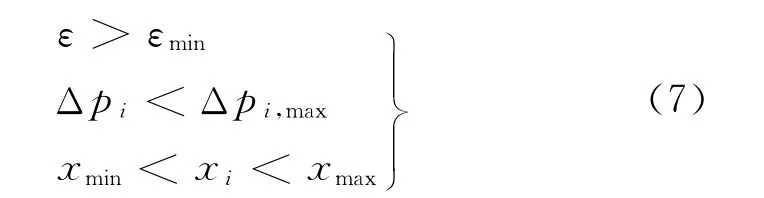
式中,εmin为允许的最低效率,值为0.75;Δph,max,Δpc,max分别为冷媒侧和空气侧允许的最大压降,值分别为50kPa和0.25kPa;xi为优化变量(Sf,δf),i表示冷媒侧、空气侧;xmax,xmin分别为每个变量优化的上下限.
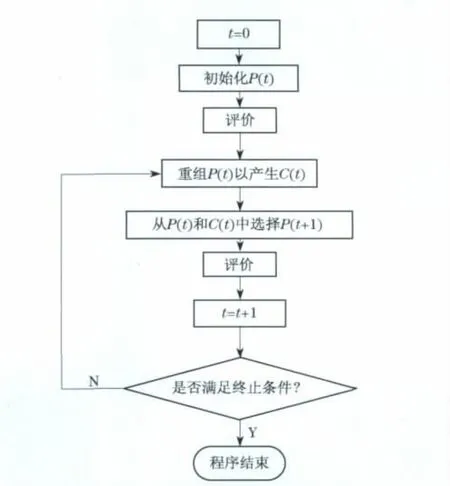
图2 遗传算法流程图Fig.2 Flow chart of GA routine
3 优化算例及结果分析
以CRH3型动车组空调系统工况为例进行优化计算,制冷剂型号为R134a,其冷凝器原始设计参数见下页表1.为了将优化结果和原始设计参数进行对比,在翅片参数变化时,若换热系数增大,换热面积相应减小(铜管总长减短),迎风面积发生改变,而管排数和其它结构参数等均保持不变.
3.1 以重量最轻为目标函数
图3(见下页)为以重量最轻为目标函数的遗传算法在优化过程中初始种群经过50次迭代后重量W随着种群大小N的变化的结果,图4为经过250次迭代后的结果.从图3和图4可以看出,在进化初始阶段,个体差异较大,经过若干代进化后,较差个体被淘汰,目标函数值变化明显.图5表示了迭代过程中种群目标函数均值的变化和最优解的变化,说明经过若干代进化之后(t>50),目标函数值最终趋于一个稳定值.
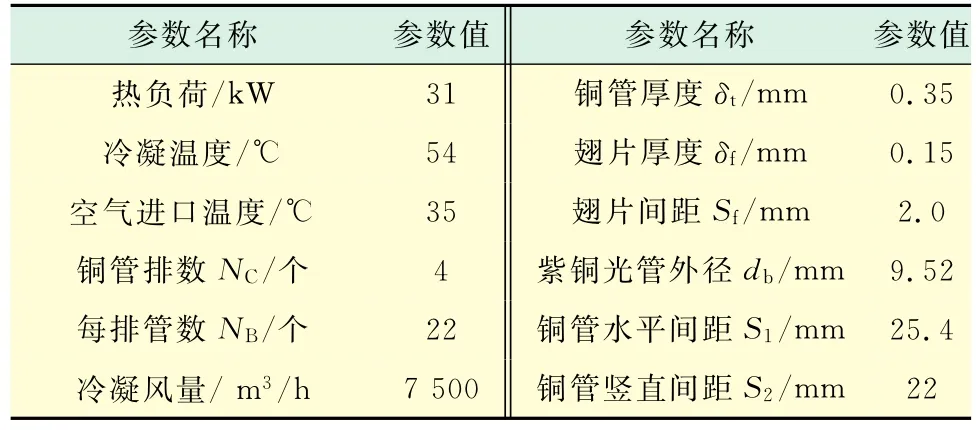
表1 冷凝器原始设计参数Tab.1 Original parameters of condenser
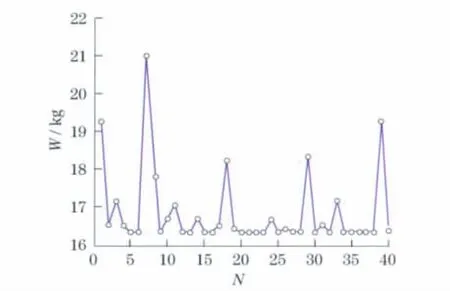
图3 经过50次迭代后的结果Fig.3 Results after 50iterations
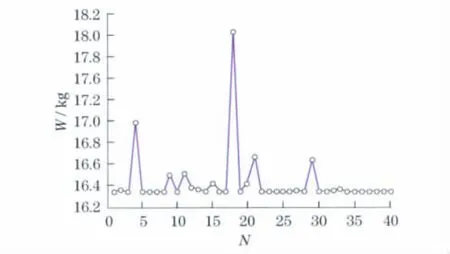
图4 经过250次迭代后的结果Fig.4 Results after 250iterations
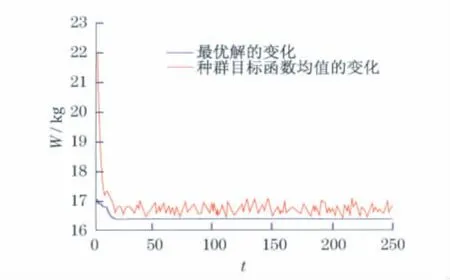
图5 重量最轻迭代中种群目标函数均值和最优解的变化Fig.5 Population means and the optimal objective changes of lightest iteration
表2为以重量最轻为目标函数的优化结果与原始数据的比较,从表2可以看出,优化结构尺寸后,翅片间距和厚度均有所减小;优化后重量减轻22.6%,体积相应减小12%,而翅片效率降低9%,但仍在允许范围内.

表2 以重量最轻为目标函数的优化结果比较Tab.2 Comparison of optimum results for minimum weight
3.2 以体积最小为目标函数
图6为以冷凝器体积最小为目标函数的遗传算法优化过程,从图6可以看出目标函数值发生明显的变化,最后趋于一个稳定值.表3为以体积最小为目标函数的优化结果与原始数据的比较.从表3可以看出,优化结构尺寸后,翅片间距有所减小而翅片厚度增加,体积减小22.7%,翅片效率增加3%,但重量比原始数据下增加11.3%,比以重量最轻为目标函数的优化结果增加43.9%.
对比表2和表3的数据,可以看到在设定范围内,翅片厚度的增加有效地减小了冷凝器的体积,同时提升了翅片的表面效率,但增大了冷凝器重量,而冷凝器的重量是列车空调机组减少原材料的消耗,降低牵引功率的重要因素之一.因此,在规定的性能要求下,如果需要同时优化重量和体积,则可建立新的目标函数φ并给出重量和体积在新目标函数中所占的权重系数,即
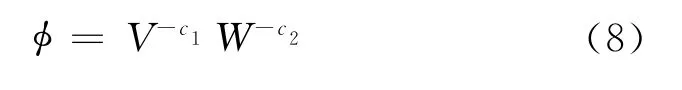
式中,c1,c2分别为体积和重量的权重系数.
由式(8)可以看出,φ越小,冷凝器越理想.若c1=0或c2=0则表示仅考虑重量或仅考虑体积.
事实上,也可以用冷凝器效率最高为目标函数进行计算,但是在列车提速和列车轻量化设计背景下,考虑较多的是冷凝器的重量和体积.当冷凝器的效率已经较高时,不宜将其作为优化目标函数,因为这往往会显著增加制造材料成本及运输费用等.
对列车翅片管式空调冷凝器采用的遗传算法的优化设计方法,可以推广到其它类型的紧凑式换热器进行优化计算.

表3 以体积最小为目标函数的优化结果比较Tab.3 Comparison of optimum results for minimum volume
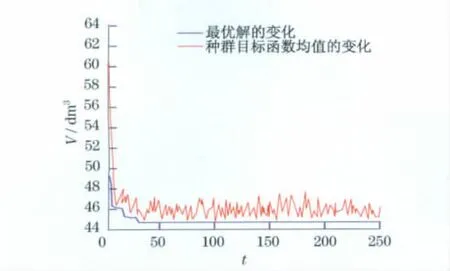
图6 体积最小迭代中种群目标函数均值和最优解的变化Fig.6 Population means and the optimal objective changes of smallest iteration
4 结 论
采用MATLAB遗传算法,以CRH3型动车组空调系统为例,分别以重量最轻和体积最小为目标函数,对翅片管式冷凝器进行了结构参数优化,可得出如下结论:
a.以重量最轻为目标函数时,通过优化计算后,翅片间距和厚度均减小;冷凝器重量可减轻22.6%,体积相应减小12%,而翅片效率降低9%,但仍在允许范围内.
b.以体积最小为目标函数时,通过优化计算后,翅片间距有所减小而翅片厚度增加,冷凝器体积减小22.7%,翅片效率增加3%.但重量比原始数据增加11.3%,比以重量最轻为目标函数的优化结果增加43.9%.
c.在列车提速和列车轻量化设计背景下,冷凝器以重量最轻为目标函数,可减少原材料的消耗,降低牵引功率,达到节能和环保的要求.如需同时考虑对冷凝器体积的优化,可建立综合考虑重量和体积的目标函数,其中重量和体积的权重系数可根据具体设计要求确定.
d.该优化设计方法可推广到其它类型的紧凑式换热器,可对不同翅片形式进行优化.
[1] 刘转华,唐阳.动车组技术[M].成都:西南交通大学出版社,2010.
[2] 谢公南,王秋旺.遗传算法在板翅式换热器尺寸优化中的应用[J].中国电机工程学报,2006,26(7):53-57.
[3] 史美中,王中铮.热交换器原理与设计[M].南京:东南大学出版社,2003.
[4] 张祉祜.制冷原理与设备[M].北京:机械工业出版社,1987.
[5] 张丽娜,杨春信,王安良.应用遗传算法优化设计板翅式换热器[J].航空动力学报,2004,19(4):530-535.
[6] Hakan A.Optimal resampling and classifier prototype selection in classifier ensembles using genetic algorithms[J].Pattern Analysis and Applications,2004,7(3):285-295
[7] 雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2011.

