基于DEA和决策树的我国工业劳动生产率影响因素规则提取
陶 洪, 徐福缘
(1.绍兴文理学院经济与管理学院,绍兴 312000;2.上海理工大学管理学院,上海 200093)
劳动生产率是指劳动者在一定时期内创造的劳动成果与其相适应的劳动消耗量的比值.劳动生产率因计算简便、含义直观,以其固有的优势一直在经济管理的理论和实践领域保持着重要的地位.劳动生产率作为衡量劳动生产效率的方法之一,不仅可以反映技术进步所造成的效率提高,也可以衡量其它替代生产因素对生产效率的影响.劳动生产率既是衡量组织竞争力的一项重要的经济统计指标,又可帮助决策者分析经济状况、预估所需劳动力以及了解促进组织成长的方法.但劳动生产率指标又是一项非常综合的指标,包含了丰富的经济信息,通过对影响劳动生产率变动的因素进行分类和规则提取,有助于更好地把握劳动生产率的增长规律.
1 理论基础
1.1 劳动生产率影响因素的DEA分析
设D1(X0,Y0)为规模报酬不变的相对效率,则规模报酬不变的C2R模型为[1]

式中,θ是相对效率;X0是投入向量;Y0是产出向量.
设D2(X0,Y0)为规模报酬可变的相对效率,则规模报酬可变的BC2模型为[2]

Kumar等[3]利用规模报酬不变模型,将劳动生产率变动分解为技术进步、技术效率和资本深化3方面的影响因素.
设由C2R模型确定的前沿面为纯前沿生产面,由BC2模型确定的为前沿生产面.t时期的前沿生产面和纯前沿生产面分别为ft,gt;t+1时期的前沿生产面和纯前沿生产面分别为ft+1,gt+1(如图1).从gt到gt+1表明从t时期到t+1时期所有决策单元不考虑规模报酬变化情况下,生产技术水平提高对生产效率的影响.
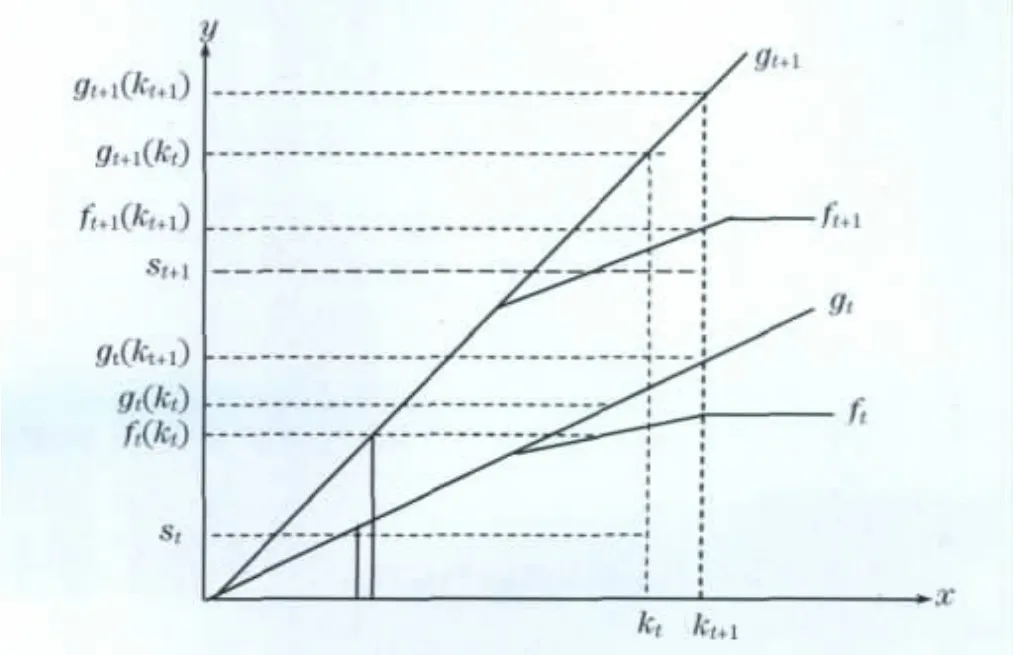
图1 劳动生产率四重分解Fig.1 Duadruplicity decomposed to labor productivity
设k表示人均资本,t期人均资本为kt,t+1时期人均资本为kt+1,t期和t+1期对应的实际劳动生产率、前沿劳动生产率和纯前沿的劳动生产率分别为st,ft(kt),gt(kt)和st+1,ft+1(kt+1),gt+1(kt+1).gt+1(kt)表示t+1时期人均资本为kt时,其纯前沿的劳动生产率;gt(kt+1)为t期人均占有资本为kt+1时,其纯前沿的劳动生产率.如果以st为参照,st和ft(kt)的差距为技术效率,这指标反映了该决策单元和人均资本占有量相同的决策单元对现有技术利用能力的差异.技术效率主要表现为管理能力、对新技术的运用能力和资源的配置能力.某一决策单元从t期到t+1期劳动生产率的变化率记为LP.技术效率的变化对劳动生产率的影响为记为TP.该指标大于1,表明可通过挖掘生产潜力提高生产效率.规模效率对生产效率的影响是记为SP.该指标度量在t期和t+1期该决策单元人均资本占有量达到最佳人均资本占有量时对生产效率的影响.处于kt和kt+1的纯技术进步变化率分别是和其几何平均是记为TC.该项指标度量从t期到t+1期技术变化对生产效率的影响,大于1,说明整体的技术水平得到提升并促进了生产效率的提高.对纯前沿生产面gt,人均资本由kt变为kt+1,劳动生产率的变化为对纯前沿生产面gt+1,人均资本由kt变为kt+1,劳动生产率的变化为资本深化对劳动生产率影响的几何平均为,记为KP.该项指标度量了在t期和t+1期人均资本的变化对生产效率的影响.由此得到劳动生产率的四重分解式

1.2 分类与规则提取的决策树算法
决策树算法是一种归纳分类算法,它通过对训练集的学习,挖掘出有用的规则.C4.5是目前广泛使用的决策树算法,该算法使用信息增益比例的概念,以信息增益比例作为选择属性的标准,在每个节点上选择具有最高信息增益比例的属性对数据集进行划分.这种理论方法使得对一个对象分类所需的期望测试数目最小,以确保找到一棵简单的树[4].
设S是s个数据样本的集合.假定类标号属性具有m个不同值,定义m个不同类Ci(i=1,…,m),设si是类Ci中的样本数.对一个给定的样本分类所需的期望信息为
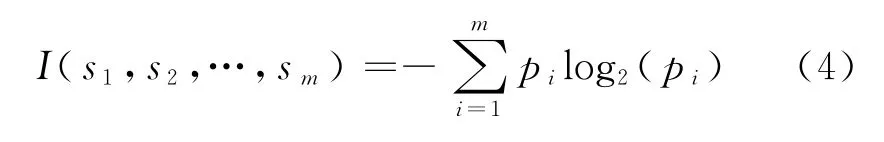
其中,pi为任意样本属于Ci的概率,并用估计.
设属性A具有v个不同值{a1,a2,…,av},可以用属性A将S划分为v个子集{s1,s2,…,sv}.其中,sj包含S中这样一些样本,它们在A具有值aj,设sij是子集sj中类Cj的样本数.根据由A划分成子集的熵(entropy)或期望信息为


在A上分枝将获得的编码信息,即信息增益为

G(A)是由于知道属性A的值而导致的熵的期望压缩.
一个属性的增益比例为
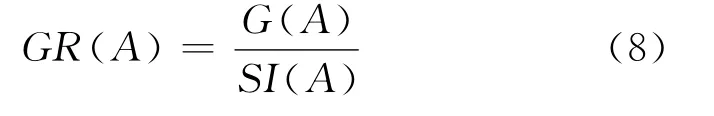
2 实证结果分析
2.1 数据的选择与处理
研究的产出数据用1988~1992年工业净产值作为产出指标,1992年之后选择了工业增加值.由于是相邻两年指标的比,《中国统计年鉴1993》提供了1992年工业净产值和工业增加值的数据,故1991~1992年的变化率按照这两年的工业净产值计算,而1992~1993年的变化率按照这两年的工业增加值计算.分析表明前期使用工业净产值和后期使用工业增加值在整个分析年度具有很强的一致性.为消除价格影响因素,对1992~2006年的工业增加值数据、1988~1992年的工业净产值数据,按统计年鉴提供的“工业品出厂价格指数”以1988年为基期进行平减.
选择各省的工业从业人员平均人数和固定资本存量作为投入指标,固定资本存量是以1988年为起点,利用永续盘存法计算而得,公式为

式中,Ki,t和Ki,t-1表示第i个省在t年和t-1年的固定资本存量;δ表示固定资产的折旧率,采用代表几何效率递减的余额折旧法得出其值为9.6%[5];Ii,t表示第i个省在第t年的固定资产投资;Pt为固定资产投资在第t年的价格指数(1988年为1).所用数据来自于《中国工业经济统计年鉴》和《中国统计年鉴》.
2.2 省域劳动生产率影响因素的分析
运用式(3)基于DEA的劳动生产率四重分解模型和中国工业统计的省份数据,对中国30个省1988~2006年的劳动生产率的变化率进行了分解,在计算过程中采用了DEAP2.1软件[6],各省域的平均结果如表1所示.
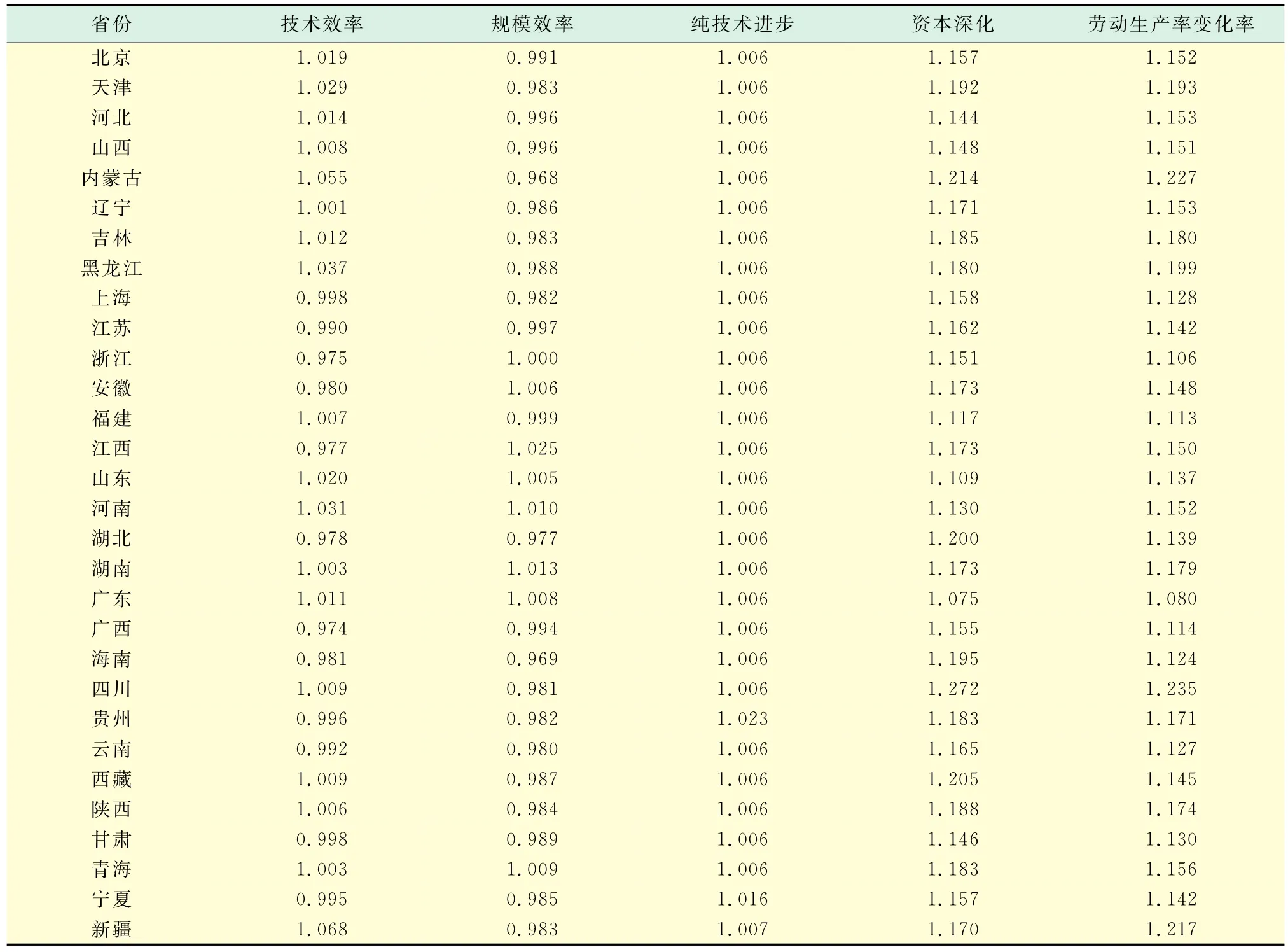
表1 省域工业劳动生产率的变化率四重分解结果Tab.1 Annual average of change for Chinese industrial labor productivity
2.3 影响省域劳动生产率变动的决策树建立和提取规则步骤
本研究中将劳动生产率作为分析目标,总结技术进步、技术效率、规模效率、资本深化4个因素对它的影响,所以将劳动生产率作为类别属性,其它4个属性称为非类别属性,提取劳动生产率变动影响规则.在决策树分析过程中,首先分别对30个省劳动生产率、纯技术效率、技术进步、人均资本的规模效率、资本深化这5个指标共18个跨年度变化率的数据进行加权平均,然后利用决策树提取影响省域劳动生产率的规则.
2.3.1 劳动生产率指标的离散化分类
由于劳动生产率指标是连续数据,首先需要对30个省的工业劳动生产率变动率的平均数据进行离散化处理,本文使用SPSS统计软件的层次聚类分析将劳动生产率增长率的数据作离散化处理,结果见表2.

表2 省域工业劳动生产率聚类分析结果Tab.2 Cluster analysis result of provincial industrial labor productivity
在用决策树分析软件Clementine对劳动生产率影响因素规则提取过程中,分别对2,3,4,5类聚类结果给予了分析,发现纯技术进步是对劳动生产率影响最小的因素,几乎不对劳动生产率指标产生影响;而且由4个聚类类别增加到5个聚类类别,分类的准确率由90%下降到86.7%,所以本次分类选取4个分类作为规则提取的分类标准.
2.3.2 基于决策树的影响省域劳动生产率变动规则提取结果
根据以上步骤,在计算过程中运用SPSS Clementine11软件,得到劳动生产率影响因素决策表的一个规则集,共包括4条规则:
a.中国工业劳动生产率增长率处于高位的省份有21个,占总数的70%;处于中上水平的省份有5个,占总数的16.7%;处于中下水平的省份有3个,占总数的10%;处于低位的省份有1个,占总数的3.3%.
b.资本深化是影响省域工业劳动生产率差异最主要的因素.资本深化以1.165作为临界点,处于临界点以上(包括临界点)和临界点以下的省份各占50%,均为15个.而工业劳动生产率增长率处于高位的21个省份中,资本深化大于等于1.165的省份有14个,占资本深化大于1.165的省份的93.3%.另外,工业劳动生产率变化率处于低位的1个省份资本深化也大于等于1.165.资本深化小于1.165的15个省份中,处于高位的省份有7个,占资本深化小于1.165的省份的46.7%;处于中上水平的省份有5个,占资本深化小于1.165的省份的33.3%;处于中下水平的省份有3个,占资本深化小于1.165的省份的20%.
c.对省域工业劳动生产率差异的影响处于第二位的指标是技术效率.从决策树分析可以知道,技术效率只对资本深化小于1.165的省份的劳动生产率变化率具有显著影响.对资本深化小于1.165的15个省份,可以按照技术效率是否大于1.003进行划分.资本深化小于1.165而技术效率大于等于1.003的省份总共有6个,并且全处于劳动生产率增长率的高位.资本深化小于1.165,技术效率也小于1.003的省份总共有9个,其中1个处于劳动生产率增长率的高位,5个处于劳动生产率增长率的中上水平,3个处于劳动生产率增长率的中下水平.
d.对工业劳动生产率影响的最后一个指标是人均资本的规模效率,并且这一指标只对资本深化小于1.165而且技术效率也小于1.003的省份具有显著影响.满足资本深化小于1.165而且技术效率也小于1.003的省份共有9个,可以按照人均资本的规模效率是否大于等于1.19分为两类.人均资本的规模效率大于等于1.19的省份有6个,其中有5个省份的劳动生产率增长率处于中上水平,有1个省份的劳动生产率增长率处于中下水平.人均资本的规模效率小于1.19的省份有3个,其中有1个省份的劳动生产率增长率处于高位,有2个省份的劳动生产率增长率处于中下水平.
3 结 论
利用决策树分类和规则提取方法,提取了劳动生产率各影响因素对省域工业劳动生产率增长差异的影响、影响方式以及影响规则.以上研究显示,中国省域间工业劳动生产率差异的决定因素是投资,即1988~2006年期间,中国工业增长仍然是依靠外延的扩展,而非依靠技术、管理等方面提升的内涵式增长.当然,由于使用的数据是多年的平均数据,无法反映时间趋势的变化,结论的精确性将不可避免受到影响,但本研究是将决策树算法用于劳动生产率分析的一次有益尝试,其结论也符合中国省域工业劳动生产率增长的现状,并对揭示中国省域工业劳动生产率增长的规律也具有一定的指导意义.
[1] Charnes A,Cooper W W,Rhodes E.Measuring the efficiency decision making unites[J].European Journal of Operational Research,1978,2(6):429-444.
[2] Banker R,Charnes A,Cooper W W.Some models for estimating technical and scale inefficiencies in data envelopment analysis[J].Management Science,1984,30(9):1078-1092.
[3] Kumar S,Russell R R.Technological change,technological catch-up,and capital deepening:relative contributions to growth and convergences[J].American Economic Review,2002,92(3):527-548.
[4] Han J,Kambr M.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2003.
[5] 张军,吴桂英,张吉鹏.中国省际物质资本存量估算:1952—2000[J].经济研究,2004(10):35-44.
[6] Coelli T.A guide to DEAP version 2.1:a data envelopment analysis program[R].Armadillo:University of New England,1996.

