集合覆盖问题降阶算法

宁爱兵， 刘艳芳， 王英磊

（上海理工大学管理学院，上海 200093）

集合覆盖问题（set covering problem，SCP）是组合优化中一个典型NP（non－deterministic polynomial time，非确定多项式时间算法）难解问题，是计算机和运筹学中的一个经典问题，在人员调动、网络安全、资源分配、电路设计、运输车辆路径安排等领域有着广泛的应用［1－4］.

对于集合覆盖问题，目前国内外主要有两种处理方法：一种是采用启发式算法［2－3］；另外一种是采用精确算法或近似算法［1，4］.各种算法的优缺点及其对比将在后面介绍.

本文将集合覆盖问题转换成二分图，再在二分图上给出降阶规则，给出上界和下界子算法，最后结合成一个新的降阶算法.

1 问题及算法介绍

1.1 问题简介

集合覆盖问题是一个优化问题，其原型是多资源选择问题.集合覆盖问题可以看作是图的顶点覆盖问题的推广，它也是一个NP难问题.

集合覆盖问题的一个实例〈X，F〉由一个有限集X及X的一个子集族F组成.子集族F覆盖了有限集X，也就是说X中每一元素至少属于F中的一个子集，即对于F中的一个子集C⊆F，若C中的X的子集覆盖了X，即，则称C覆盖了X.集合覆盖问题就是要找出F中覆盖X的最小子集C＊，使得｜C＊｜＝min｛｜C‖C⊆F且C覆盖X｝.

1.2 问题转换

在算法处理之前，将该问题转换成二分图来进行处理，转换方法如下：

将集合覆盖问题〈X，F〉中X的每个元素作为二分图的一个顶点子集X，把F中的每个元素作为二分图的另一个顶点子集F，F中的元素是集合.若F中的元素f1包含X中的元素x1，则在f1与x1之间连线，否则不连线.

这样处理后，得到一个图G＝（V，E），其中，V＝X∪F，E＝｛（x，f）｜x∈X，f∈F且x∈f｝.很显然，图G是二分图.而原问题的求解变为在顶点子集F中找出一个最小的子集C＊，使得顶点子集X中的每一个顶点至少与C＊中的顶点有一条边相连.

1.3 数学符号

为了方便描述，除了问题简介和问题转换中定义的符号外，还定义如下符号：

n表示二分图G中顶点集X中结点的个数；

m表示二分图G中顶点集F中结点的个数；

d（vi）表示结点vi的度，其值为与vi关联边的条数；

N（vi）表示二分图中顶点vi的邻点集，N（vi）＝｛vj｜（vi，vj）∈E｝；

Φ表示空集；

b表示最小覆盖子集C＊中元素个数的下界，即｜C＊｜≥b；

u表示最小覆盖子集C＊中元素个数的上界，即｜C＊｜≤u.

1.4 下界子算法

对X中的元素xi，由于必须至少有1个集合覆盖它，也就是说C＊中至少有1个结点要与它关联，因此N（xi）至少有1个结点在C＊中，故有下面的下界子算法.

a.i＝1；

b.集合temp＿c＝Φ；

c.若i＞n或者temp＿c中元素的数量为m，则整个算法结束并得到下界b；

d.对X中的元素xi，若N（xi）∩temp＿c＝Φ，则i＝i＋1，b＝b＋1，temp＿c＝N（xi）∪temp＿c并跳至第c步，否则执行i＝i＋1并跳至第c步.

算法中的N（xi）∩temp＿c＝Φ说明目前还没有集合覆盖xi.

1.5 上界子算法

采用如下贪心算法求解上界u：

a.令G2为待处理的二分图，X2＝X，F2＝F；

b.u＝0，集合temp＿c＝Φ；

c.若X2为空集，则算法结束，否则跳至第d步；

d.在F2中找出1个度最大的结点f1，其中f1∈F2；

e.u＝u＋1，temp＿c＝temp＿c∪｛f1｝，在二分图G2中删除结点f1及其关联边，F2＝F2－｛f1｝，删除集合N（f1）中的结点及其关联边，X2＝X2－N（f1），修改对应结点的d（vi），跳到第c步.

该子算法对图的删除操作都是在临时变量图G2中进行的，不影响原来的二分图.

1.6 降阶规则

规则1 对顶点集X中度为1的结点xi，其关联边对应的另一个结点fj一定在最小子集C＊中.

证明 因为度为1的结点xi必须被某个集合覆盖，而xi仅仅只属于一个集合fj，故要覆盖xi，则fj一定在最小子集C＊中.

规则2 对顶点集F中的两个元素f1和f2，若N（f1）⊆N（f2），则可以将顶点f1及其关联边从图中删除而不会影响最小的子集C＊求解.

证明 因为N（f1）⊆N（f2），所以f1所起到的覆盖作用完全可以由f2来代替.代替后的覆盖功能只会更强，而不会更弱，而目标函数最小子集C＊中的数量不变.因此可以把顶点f1及其关联边从图中删除而不会影响最小子集C＊求解.

在降阶的中间过程中，可能会出现度为0的结点，也可能在F中存在1个能覆盖X中所有结点的子集合f1，此时采用规则3和规则4来降阶.

规则3 在降阶的任何过程中，可以将顶点集F中度为0的结点f1直接从图中删除.

证明 由于顶点集F中度为0的结点f1不能覆盖任何结点，因此可以直接删除.

规则4 在降阶的任何过程中，若顶点集F中存在一个结点f1覆盖X中的所有结点，则将f1加入到最小子集C＊中.

证明 由于此时X中还有结点没有被覆盖，故至少需要在F中找出一个子集合来覆盖，而能在F中找到一个能覆盖X中的所有结点的子集合f1，则可以将f1加入到最小子集C＊中.

其它的降阶方法在后面的算法中介绍.

1.7 降阶算法

对于已经转成二分图的问题，采用如下算法进行降阶：

a.下界b＝0，C＊＝Φ；

b.调用下界子算法求出下界b；

c.按照规则1，对于X中度为1的结点xi，把其关联边对应的另一个结点fj加到最小子集C＊中，b＝b－1，并把结点xi及其关联边从图中删除.将结点fj、结点集合N（fj）及其关联边从图中删除，并修改对应点的度d（vi），修改变量n和m.这样持续做下去，直到X中不存在度为1的结点为止；

d.按照规则2，对顶点集F中的两个元素f1和f2，若N（f1）⊆N（f2），则可以把顶点f1及其关联边从图中删除并修改对应点的度d（vi），同时修改变量m；

e.若d中删除过结点，则跳到第c步，否则执行下一步；

f.采用规则3和规则4来降阶，调用上界子算法求出上界u，若此时u＝b，则令C1为上界子算法中的temp＿c，此时C＊＝C＊∪C1为最优解，整个算法结束；

g.j＝0；

h.若j＞m，则跳到第o步；

i.对F中的元素fj，令N2（fj）为N（fj）中度为2的结点集合，若N2（fj）中结点数量大于等于u，则执行下一步，否则跳到第n步；

j.集合temp＿c＝Φ；

k.把N2（fj）中每一个结点vi的邻点集N（vi）加到集合temp＿c中；

l.temp＿c＝temp＿c－fj（这里操作的含义是假设fj不在最小子集C＊中）；

m.若temp＿c的数量大于u，则把结点fj加到最小子集C＊中，把结点fj和结点集合N（fj）从图中删除，同时执行m＝m－1，n＝n－｜N（fj）｜，u＝u－1，并修改对应点的度；

n.采用规则3和规则4来降阶；j＝j＋1，跳到第h步；

o.若在第h至n步中删除过结点，则跳到第c步，否则整个算法结束.此时C＊中的元素是在最小集合覆盖中的元素，若此时图为无边的空图，则得到最小集合覆盖C＊，否则说明只是降低了问题的规模和难度，但没有得到最终的最优解.

算法中的第i到第l步是利用反证法降阶，即假设fj不在最小集合覆盖C＊中时，若能判断此时要加入到C＊的元素个数大于上界u，则说明出现矛盾，因此fj一定在最小集合覆盖C＊中.

1.8 算法的时间复杂度分析

下面的分析，都是指在最坏情况下的时间复杂度.

问题转换的时间复杂度为O（nm），下界子算法为O（nm2），上界子算法为O（nm），降阶算法的第c步为O（n），第d步为O（n2m2），第h步到第n步为O（n2m），因此整个算法的时间复杂度为O（n2m3）.

2 示例分析

为了更清楚地了解算法的原理及应用情况，下面给出3个示例来进行分析.

示例1 求图1（见下页）中图G的最小集合覆盖，其中，X＝｛a，b，c，d，e，f，g，h，i，j，k，l｝，F＝｛s1，s2，s3，s4，s5，s6｝，s1＝｛a，b，e，f，i，j｝，s2＝｛f，g，j，k｝，s3＝｛a，b，c，d｝，s4＝｛e，f，g，h｝，s5＝｛i，j，k，l｝，s6＝｛d，h｝，该示例取自文献［1］，文献［1］提供的近似算法.

分析方法一：

Step 1 先把图1转成如图2（见下页）所示的二分图；

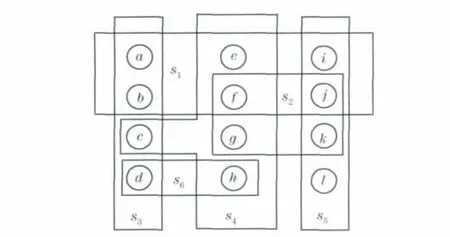
图1 示例1Fig.1 Instance 1

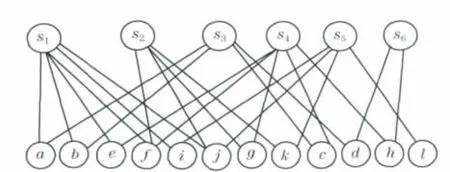
图2 二分图Fig.2 Bipartite graph

Step 2 调用下界子算法求出下界b＝3；

Step 3 按照规则1，对于X中度为1的结点l，将其关联边对应的另一个结点s5加到最小子集C＊中，得C＊＝｛s5｝，b＝b－1＝2，并将结点l及其关联边从图中删除，把结点s5、结点集N（s5）及其关联边从图中删除，并修改对应点的度d（vi），修改变量n＝8和m＝5，得到图3所示的图形；

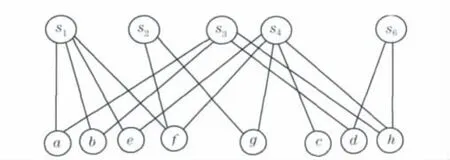
图3 二分图Fig.3 Bipartite graph

Step 4 按照规则2，对顶点集F中的两个元素s2和s4，由于N（s2）⊆N（s4），所以可以将顶点s2及其关联边从图中删除并修改对应点的度d（vi），同时修改变量m＝5－1＝4，得到图4所示的图形；

Step 5 按照规则1，对于X中度为1的结点g，把其关联边对应的另一个结点s4加到最小子集C＊中，得C＊＝｛s4，s5｝，b＝b－1＝1，并将结点g及其关联边从图中删除，把结点s4、结点N（s4）及其关联边从图中删除，并修改对应点的度d（vi），修改变量n＝3和m＝3，得到图5所示的图形；

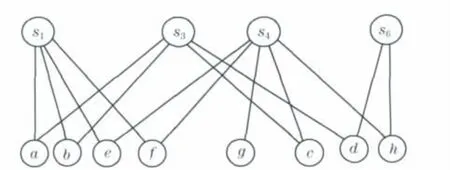
图4 二分图Fig.4 Bipartite graph

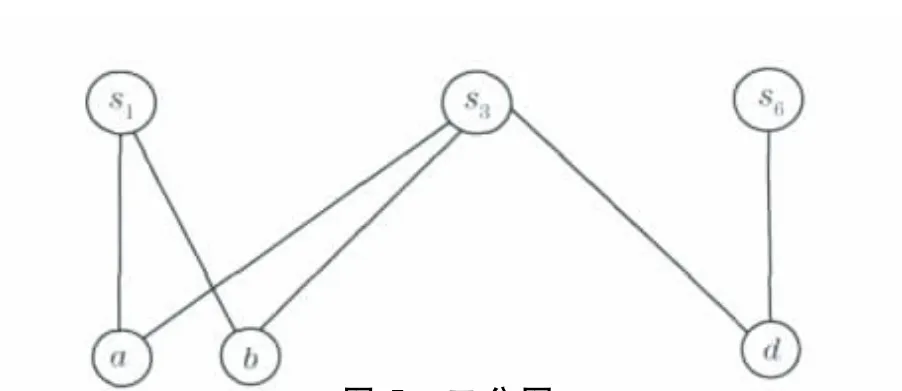
图5 二分图Fig.5 Bipartite graph

Step 6 执行算法的第f步，求得上界u＝1，此时u＝b，得到最优解C＊＝｛s3，s4，s5｝，整个算法结束.

分析方法二：

为了演示降阶算法中的第h到第n步，下面不使用规则2来降阶，也不使用算法第f步中的u＝b的方法来降阶.

这里的第1，2，3步同分析方法一中的完全相同，此时得到图3所示的图形.

Step 7 执行算法的第f步，求得上界u＝2；

Step 8 执行算法的第i步，对F中的元素s3，N2（s3）＝｛a，b，c，d｝为N（s3）中度为2的结点集合，由于N2（s3）中结点数量大于等于u，则跳到算法的第j步；

Step 9 执行算法的第j步，集合temp＿c＝Φ；

Step 10 执行算法的第k步，将N2（s3）＝｛a，b，c，d｝中每个结点vi的邻点集N（vi）加到集合temp＿c中，得temp＿c＝｛s1，s3，s4，s6｝；

Step 11 执行算法的第l步，得temp＿c＝temp＿c－fi＝｛s1，s4，s6｝

Step 12 执行算法的第m步，C＊＝｛s3，s5｝，将结点s3、结点集N（s3）从图中删除，m＝m－1＝4，n＝4，u＝u－1＝1，得到图6；

Step 13 执行算法的第n步，采用规则4来降阶得到最优解C＊＝｛s3，s4，s5｝.

示例2 X＝｛1，2，3，4｝，F＝｛s1，s2，s3，s4｝，其中s1＝｛1，2｝，s2＝｛2，3｝，s3＝｛3，4｝，s4＝｛4，1｝.

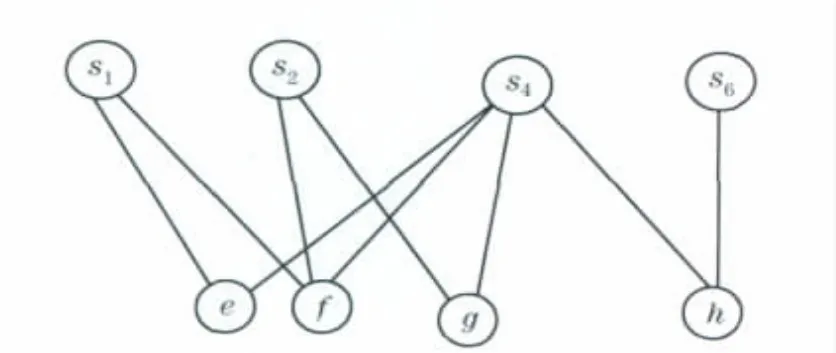
图6 二分图Fig.6 Bipartite graph

分析：

由下界子算法求得b＝2，当执行算法的第f步时，由上界子算法求得u＝2，由于u＝b，因此，求得最优解为C＊＝｛s1，s3｝.

示例3 X＝｛a，b，c，d，e，f｝，F＝｛s1，s2，s3，s4，s5｝，其中s1＝｛a，b｝，s2＝｛a，f｝，s3＝｛d，e｝，s4＝｛c，e｝，s5＝｛b，c，d｝.

分析：

step 1 先将该问题转成如图7所示的二分图；

step 2 按照规则1，并将s2加到最小子集C＊中，得C＊＝｛s2｝，将结点s2、结点集N（s2）及其关联边从图中删除；

step 3 按照规则2，将s1及其关联边删除；

step 4 再按照规则1，将s5加到最小子集C＊中，得C＊＝｛s2，s5｝，将结点s5、结点集N（s5）及其关联边从图中删除；

step 5 最后将s3加到最小子集C＊中，得到最优解C＊＝｛s2，s3，s5｝，或者把s4加到最小子集C＊中，得到最优解C＊＝｛s2，s4，s5｝.

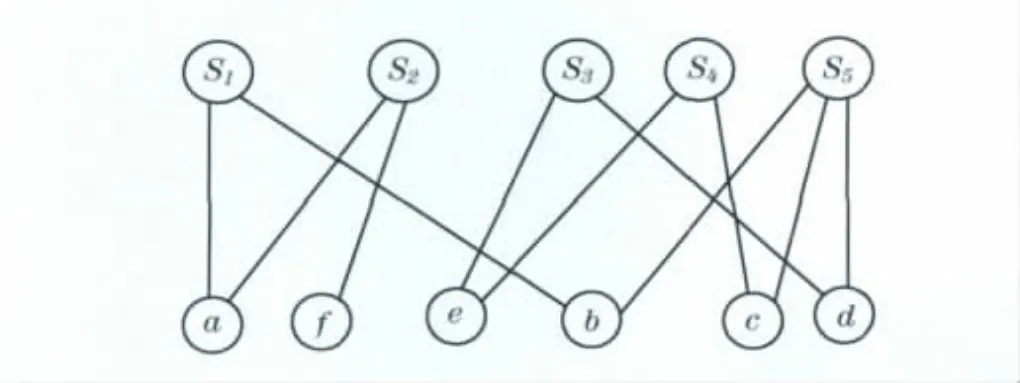
图7 二分图Fig.7 Bipartite graph

3 算法对比分析

对于集合覆盖问题，目前国内外主要有两种处理方法：一种是启发式算法［2，3］，启发式算法的优点是能够快速得到可行解，其缺点是不能保证解是最优解，也不能提供解的近似比；另外一种是采用精确算法或近似算法［1，4］，比如分枝定界法、回溯法等，精确算法的优点是能得到最优解，但时间复杂度都是指数级别的，难以处理规模较大的问题，近似算法在近似程度上提供保障，但不能得到最优解.

本降阶算法的优点在于利用问题的性质及上下界来加快问题的求解速度，使原问题变为规模更小的同性质的子问题，便于进一步的处理；不足之处在于只能对部分实例问题求解得到最终解，对不能得到最终解的问题实例还必须与其它方法结合起来才能得到最终解，比如对于经过降阶算法处理后的子问题，若规模较少，可以用分枝定界法来得到最优解，若规模仍然很大，则可以用启发式算法来求解.

4 结束语

集合覆盖问题是不具有多项式时间算法的NP难题，本文提供的降阶算法能在一定程度上降低原问题的求解规模与难度，而且在某些情况下，能直接得出问题的最优解.该方法不仅可以单独使用，而且可以与其它方法结合起来使用，从而加快问题的求解速度.

［1］ 王晓东.计算机算法设计与分析［M］.3版.北京：电子工业出版社，2007.

［2］ 陈端兵，黄文奇.一种求解集合覆盖问题的启发式算法［J］.计算机科学，2007，34（4）：133－136.

［3］ Chvatal V.A greedy heuristic for the set covering problem［J］.Mathematics of Operations Research，1979，4（3）：233－235.

［4］ Hassin R，Levin A.A better than greedy approximation algorithm for the minimum set cover problem［J］.SIAM Journal on Computing，2005，35（1）：189－200.