PROMETHEE方法在城市环境空气质量评价中的应用
胡 君, 蒋 艳
(上海理工大学管理学院,上海 200093)
随着经济的高速发展,生活水平的不断提高,人们越来越关注生存的环境,国内外关于环境质量评价方法的研究也日趋活跃.空气质量是环境质量中的一个重要组成部分.目前空气质量评价方法很多,如API法、模糊综合评判法、灰色聚类关联分析法及神经网络法等[1].由于我国各大城市地理环境和发展程度的差异,工业废气和汽车尾气的排放程度级别和限制措施的力度不同,导致环境空气质量评价的差异性和复杂性.环保政策实施得好,市民的环保意识高,则其环境空气质量也就更高.如何客观地评价出不同城市环境空气质量的优劣,解决其自身所存在的复杂性以及评价过程中的复杂性,是本研究的目的所在.
本文在相关研究结果的基础上,采用样本城市的环境空气质量作为评价对象,以对样本进行监测所得的可吸入颗粒物(PM10)、二氧化硫(SO2)和二氧化氮(NO2)这3个因子为评价指标,设置了相应的评价指标体系,并通过熵值法确定各指标的权重以避免权重确定的主观性[2].评价结果显示本文所采用方法的适用性和可靠性.
1 指标体系模型的构建
1.1 评价指标的确定
根据国家空气质量评级标准GB3095—1996(见表1)可以知道,影响城市环境空气质量的主要因素可从3个方面考虑:PM10,SO2和NO2,监测的指标属性值均为年平均量.级别越高,环境空气污染越严重,空气质量自然越差.
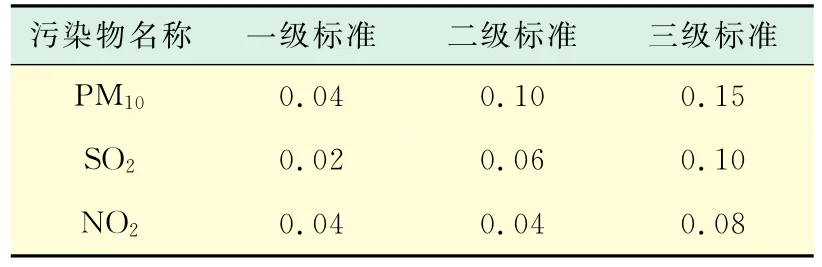
表1 空气质量评级标准Tab.1 The evaluation standard mg/m3
1.2 方案集的确定
为了具体说明方法的使用,选取了2009年统计年鉴中的8个城市——北京、哈尔滨、上海、合肥、乌鲁木齐、海口、重庆和拉萨分别作为评价样本,即样本集A:{A1,A2,A3,A4,A5,A6,A7,A8}.经过一定地整理后得到相关的指标数值.各个方案与其相对应的属性值所构成的评价模型如表2所示.可以根据最后的排序结果来估计8个样本的空气质量的排序.
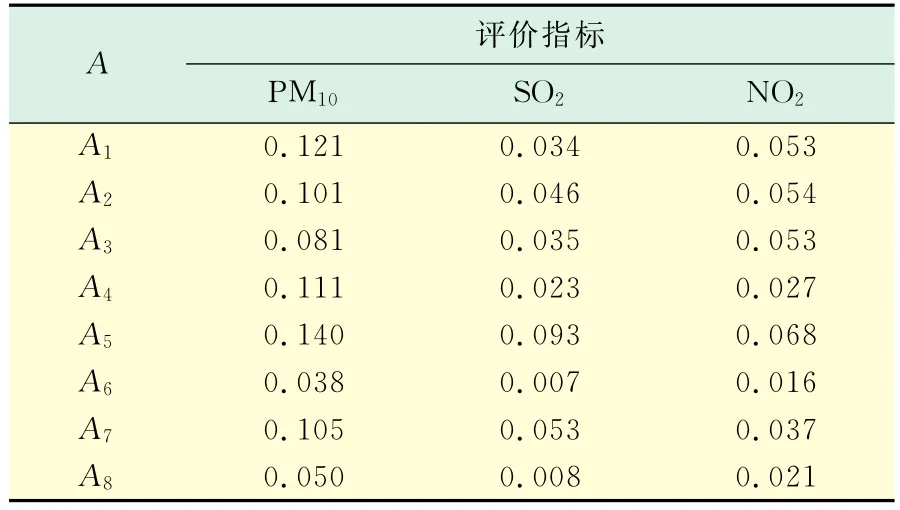
表2 评价模型Tab.2 The evaluation model mg/m3
1.3 权重的确定
由于各污染物对大气环境质量的影响程度不同,所以应赋予它们不同的权重值.多指标的综合评价因子权重的确定方法,大体可分为主观赋权法和客观赋权法两类.在这里采用客观赋权法中与多属性决策分析联系比较紧密的熵值法来确定权重[3].
首先考虑一个方案评估的问题,设有m个评价对象(方案),n个评估指标,按照定性与定量相结合的原则构建一个多对象关于多指标的评价矩阵R=(xij)m×n,其中xij为对象ai在第j个评价指标xj下的属性值,因此这个矩阵称为属性值矩阵.
对于属性值矩阵R=(xij)m×n,由熵的定义,在有m个评价对象,n个被评价指标的评估问题中,第j个评价指标的熵定义为
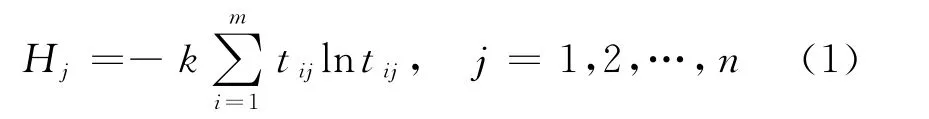
第i个指标的熵权定义为
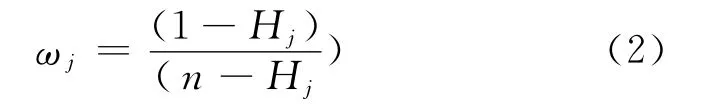
1.4 PROMETHEE法
PROMETHEE法是一种基于方案的两两比较的多属性决策分析方法,它是建立在“级别优先于”关系上的排序方法.PROMETHEE法由PROMETHEEⅠ法和PROMETHEEⅡ法组成,PROMETHEEⅠ法在方案集A上建构一个部分序,而PROMETHEEⅡ法则在方案集A上建构一个完全序[4].其基本原理为:
考虑一个有限m个的可能方案城市集A={A1,A2,…,Am},有n个数字型属性,其属性值矩阵R=(xij)m×n,i=1,2,…,m,j=1,2,…,n.由表2中的评价标准可知,将最终的评价结果设定为各个城市的污染严重程度,并按照由大到小进行排序,所以对空气质量的评价指标的属性为效益型,即所有属性的值越大越优,空气的质量相对就越差.其具体步骤如下:
a.确定每个指标的优先函数
优先函数的概念就是在效益型指标xj下,对象城市Ai优于另一个对象Ar的程度.其形式为
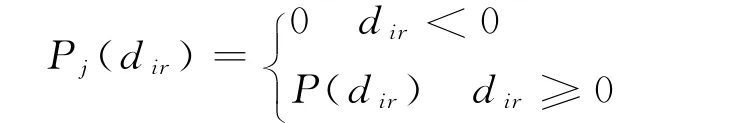
其中,dir=xij-xrj(i,r=1,2,…,m;j=1,2,…,n)
在实际的应用中,PROMETHEE法一般提供了6种可供选择的优先函数,决策者可以根据自身的偏好结合实际为每个指标选择优先函数,当然决策也可以另行构造准则.这里采用具有线性优先关系的函数来对每一个指标进行评价,该函数准则允许决策者在d<m之内其偏好强度对d的增加而线性增长[5],即
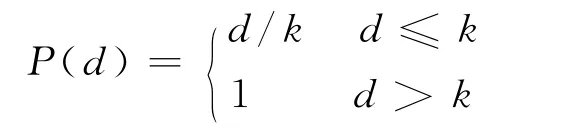
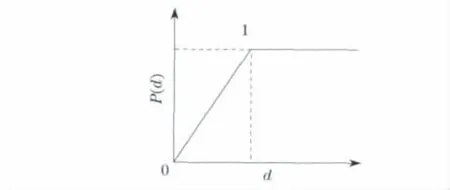
图1 P (dir )的函数图像Fig.1 The function image of P (dir)
b.确定指标/准则的相对重要性(权重)
确定指标权重W={ω1,ω2,…,ωn},ωj(j=1,2,…,n)表示指标j的相对重要性的度量.在这里就是熵权.
c.确定优先指数
多准则优先指数定义为
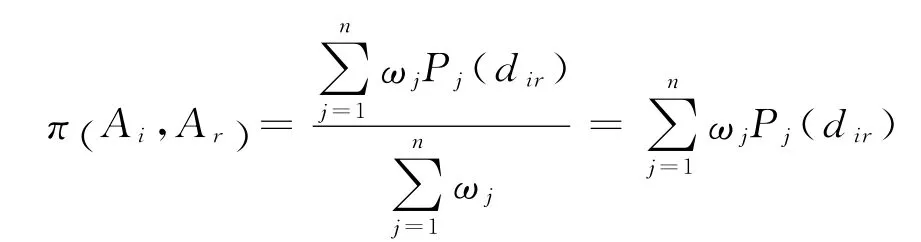
其中,i,r=1,2,…,m;j=1,2,…,n
π(Ai,Ar)是决策者同时考虑所有指标时,对方案城市Ai与Ar的优先强度的描述.
d.确定每个对象的流出和流入
流出定义为
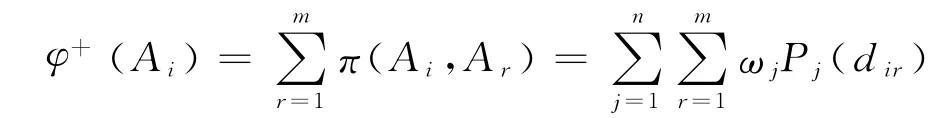
其中,r≠i
流入定义为
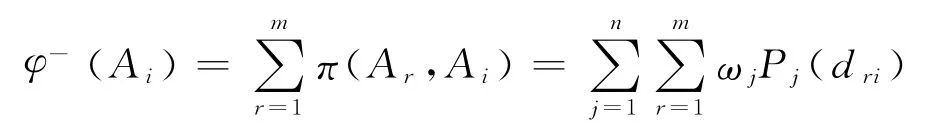
其中,i≠r
式中,φ+(Ai)为方案城市Ai的流出,即表示Ai级别优于其它对象的可能性,它的值越大,Ai相对于其它方案的级别就越高;φ-(Ai)为方案城市Ai的流入,即表示其它方案的级别优于Ai的可能性,一般而言,其值越小,该对象方案的级别越好.因此,可以得到部分序{P(1),I(1),R}.其中,P表示级别优先于关系,I表示等价关系,R则表示两个方案之间是不可比的.
e.确定完全序
以上4步为PROMETHEEⅠ法的基本步骤,它只能得到所有城市方案集A上的偏序.通过使用PROMETHEEⅡ法在A上才可以得到完全序{P(2),I(2)},各方案Ai的净流量为
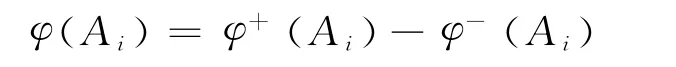
据各方案净流量的大小,可确定其优先关系为
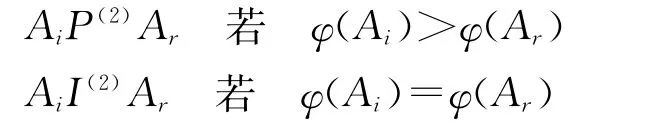
2 模型的评价和分析
2.1 构建模型矩阵
表2中每个评价指标相对于空气污染程度而言都为效益型指标,即属性值越大,空气污染程度越严重.它们的优先函数均为线性优先函数(Ⅲ),而且函数参数k值取各指标属性值的最大与最小值之差,表2中求得kPM10=0.102,kSO2=0.086,kNO2=0.052.
2.2 权重值确定
根据上述熵值法计算式(1)和式(2)求得各指标的权重见表3。
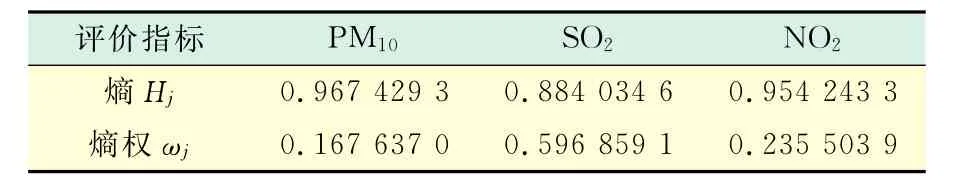
表3 指标权重Tab.3 The weight of every evaluation index
2.3 排序结果分析
根据以上决策矩阵及其优先函数参数和权重,用PROMETHEE法所求得的π(Ai,Ar)如表4所示,φ+(Ai),φ-(Ai)和φ(Ai)的值见表5.
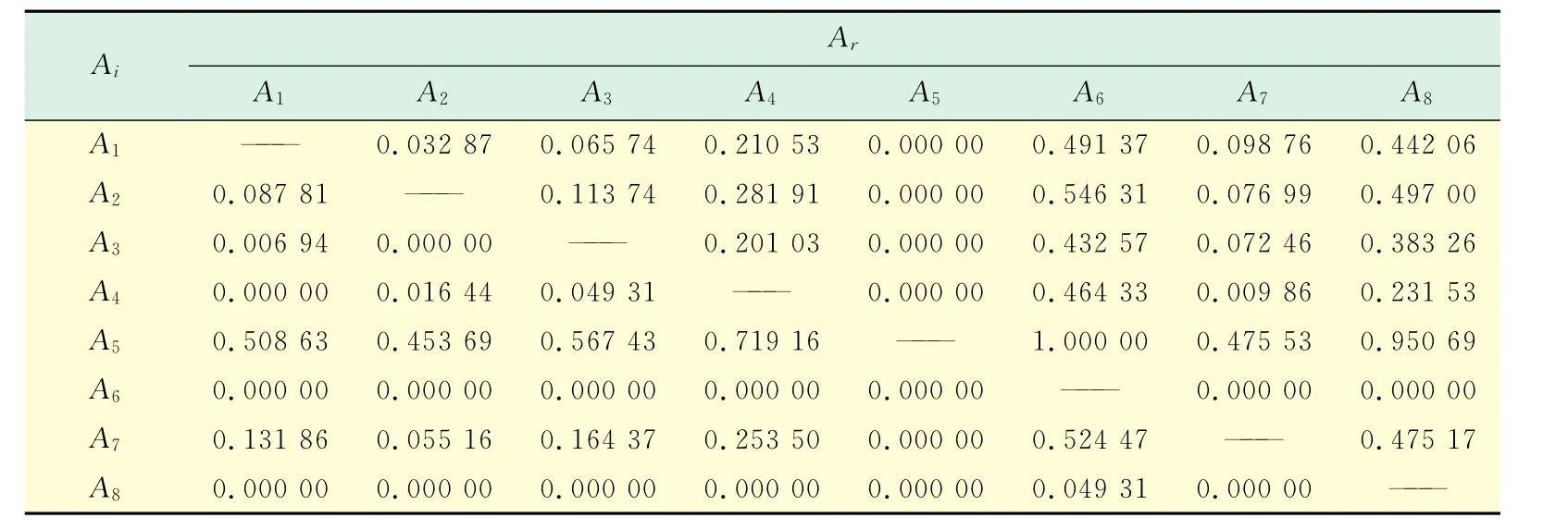
表4 各方案对的π(Ai,Ar)值Tab.4 The value ofπ(Ai,Ar)of each scheme pair

表5 各方案的φ+(Ai),φ-(Ai)和φ(Ai)的值Tab.5 The value ofφ+(Ai),φ-(Ai)andφ(Ai)of each scheme
据表5中的φ+(Ai)的数据(由大到小)、φ-(Ai)的数据(由小到大),由PROMETHEEⅠ法可以得到方案集A上的部分序,如图2所示.
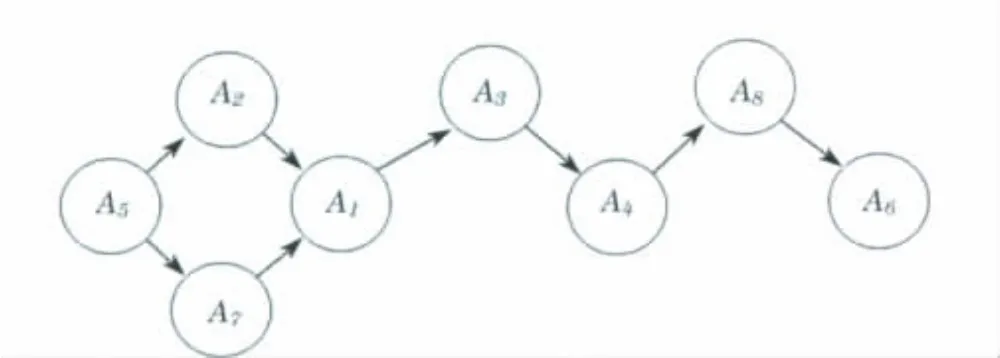
图2 PROMETHEEⅠ法的排序关系图Fig.2 The advantage relation graph of PROMETHEEⅠmethod
图2中方案A2与A7之间是不可比的,故排序关系为部分序.由PROMETHEEⅡ法对φ(Ai)的数据的大小进行排序,从而可以得到各个城市的空气质量受污染程度的完全序关系图,如图3所示.
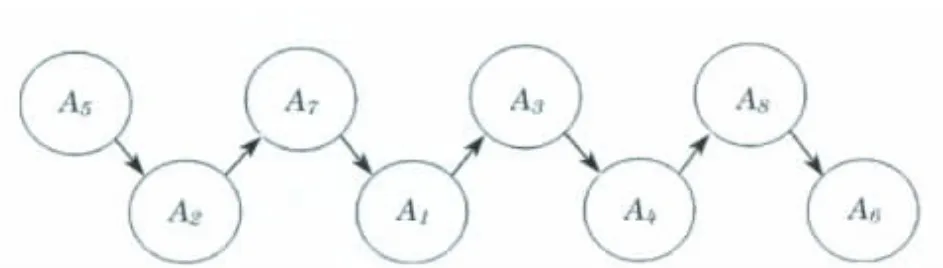
图3 PROMETHEEⅡ法的排序关系图Fig.3 The advantage relation graph of PROMETHEEⅡmethod
由图3的排序结果可知,首先A5即乌鲁木齐市的环境污染最严重,空气质量也是所有城市当中最差的,主要是因为其地处沙漠的地理位置有关;其次是东北的哈尔滨A1、山城重庆A7、北京A1、上海A3及合肥A4;最后,空气质量最好的是拉萨A8与海口A6,拉萨因为地处高原,海拔高,人烟稀少,季节也以雨雪多,而海口则因其地处岛屿,一年四季以海洋性气候为主,并且发展旅游业和农业,所以空气质量自然最好.很显然理位置和区域经济的发展对各城市的评价结果有很大的影响,但各城市还是要根据各自的实际发展情况采取相应的环保政策,以便更好地提高各城市的环境空气质量,最终改善市民的呼吸质量.
3 结束语
使用PROMETHEE方法来对城市环境空气质量的优劣进行评价排序,结果与实际情况基本符合.并且该方法无需对原始数据进行预处理,避免了信息的偏离,增强了评价的客观性和科学性.
PROMETHEE法一般提供6种可供选择的优先函数,在本文中采取的是线性优先函数(Ⅲ)来描述各指标属性值的差别与目标达到程度之间的关系.当然还要根据数据的自身特点来选择最佳的优先函数及参数.确定指标权重采用的熵值法是通过计算样本自身数据对权重做出判断,避免了人为的主观性和随意性,保持了样本指标的数据独立性,但熵值法确定指标的权重也存在一定局限性,如容易忽略不同指标数据之间的关联性.因此在很多情况下,可以将该决策方法中的客观熵权与专家的主观权重结合进行决策评价.
城市环境的空气质量的评价是一个很复杂的课题,涉及的方法也很多,有待于进一步研究和探讨.
[1] 张云海,马雁军,孙财涛,等.灰色聚类评价在经济区大气环境质量评价中的应用[J].环境科学与技术,2010,33(6):426-428.
[2] 李维,杨保安,周力.基于PROMETHEE II法和熵值法的城市新型工业化评价[J].郑州航空工业管理学院学报,2007,25(3):19-22.
[3] 邱菀华.管理决策与应用熵学[M].北京:中国电力出版社,2011.
[4] Jiang Y,Tian D G,Pan Y.Ranking environmental projects model based on multicriteria decision-making and the weight sensitivity analysis[J].Journal of Systems Engineering and Electronics,2007,18(3):534-539.
[5] 岳超源.决策理论与方法[M].北京:科学出版社,2002.

