微/纳米传动平台的模态试验及优化设计
林 超,俞松松,程 凯,王勇勤,崔新辉,陶友淘
(重庆大学 机械传动国家重点试验室,重庆 400030)
目前,在高精密领域,尤其在纳米技术中,微/纳米传动平台的地位越来越高,比如微/纳米图像成型[1]、生物工程与医疗器械[2]、扫描探针显微镜检测[3]、光学器件微装配[4]、MEMS 的微制造[5]等。同时,也对传动平台的提出了诸多设计要求,既要求平台具有大行程、纳米级分辨率及良好的紧凑性,又要具有高稳定性、高带宽、高速及高加速等优点[6]。基于压电陶瓷驱动和柔性机构的平台[7-9],可克服机械摩擦、机械间隙,近年来,已得到了越来越广泛的应用。林超等[10]设计了5自由度微/纳米传动平台,由压电陶瓷驱动,利用柔性机构弹性变形实现高精密传动,可满足纳米级分辨率的设计要求。但是,平台的高速高加速和高精度是相互矛盾的,由于柔性机构的弹性,在实际工作中不可避免地会产生振动[11],严重影响平台的动态性能、传动精度和疲劳寿命。同时,平台在高速高加速情况下,具有较为明显的时变模态特性[12],而利用模态试验分析对模态参数辨识的方法[13],可应用于平台结构性能的评价、结构动态修改和优化设计等研究中,模态试验识别出的模态参数对提高平台的精度和可靠性起着重要作用[14]。
本文针对5-DOF微/纳米传动平台,采用理论动力学建模和有限元方法,对平台的模态和振动进行了研究,并分析了柔性板簧厚度、长度对平台固有频率的影响,得到了其变化规律。通过优化柔性板簧厚度、长度设计的两个平台,分别对其进行了模态试验分析,阐述了模态试验过程和方法,并识别出了两个平台的固有频率、阻尼比和模态振型等模态参数,为平台的结构优化设计、控制方法提供了试验依据。
1 动力学建模
设计的5自由度微/纳米传动平台,如图1所示,由于平台是由整块金属材料经钻、铣、磨及线切割等工艺加工而成的一体式结构,无须机械安装,且6个柔性分支之间由柔性板簧(线切割去除两侧多余金属而成)连接,通过4个安装固定孔将平台固定在基座上,安装固定孔的下端铣有凸台,将平台悬置,如图2(a)所示,避免了平台与基座之间的摩擦,因此阻尼非常小(几乎为0),可将平台视为无阻尼的多自由度系统[15],应用拉格朗日方程,可建立平台的动力学模型,如式(1)所示,从而得到平台的固有频率和模态阵型。

图1 微/纳米传动平台实物Fig.1 Mirco/nano-transmission platform
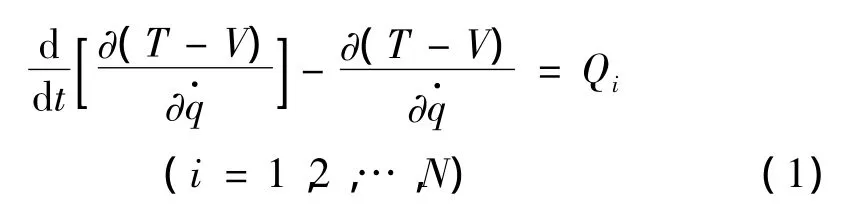
式中:T为系统的总动能;V为系统的总势能;Qi为广义力;qi为广义坐标;N为系统的自由度数;
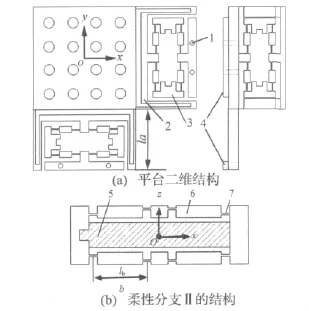
图2 平台二维结构和柔性分支Ⅱ的结构Fig.2 Architecture of the platform and flexible limbⅡ
由图1和图2可知,柔性分支由多个柔性板簧和刚性杆构成,各刚性杆由柔性板簧连接,布置在xoy平面的柔性分支Ⅰ结构完全一样,见图2(a),且布置在xoz和yoz平面的4个柔性分支Ⅱ结构完全一样,如图2(b)所示。每个柔性分支由一个压电陶瓷驱动,通过控制各个压电陶瓷的电压量,压电陶瓷由于压电效应可实现自身的伸长/收缩,因此,根据平台的几何特征,平台的自由度为5,其传动输出为δ=[ΔxΔyΔzθxθy]。
由图2可知,相对于刚性杆,柔性板簧的质量非常小,为了模型建立和计算方便,可忽略柔性板簧的质量不计,且只考虑其弯曲刚度,不考虑柔性板簧的拉伸变形。根据式(1)的拉格朗日方程,平台的动能可表示为:
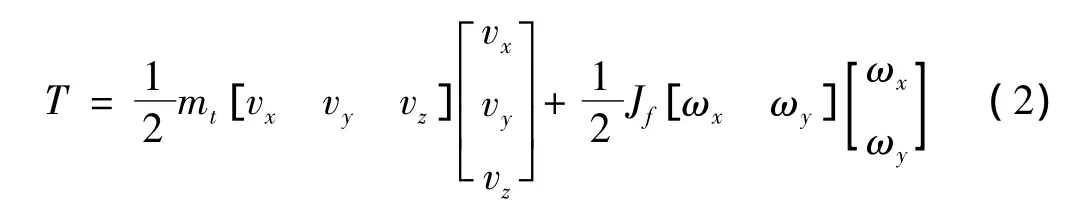
式中:mt为平台的总质量;vx,vy,vz为平台沿x,y,z向的传动速度;Jf为平台上表面的转动惯量;ωx,ωy分别为平台上表面绕x、y向的角速度。其中,vx=Δ,vy=,mf为平台上表面的质量,s为平台上表面的宽度。
平台实现各自由度传动时,系统势能主要为柔性板簧的弹性势能和平台的重力势能,由于平台z向的传动行程非常小(小于0.5 mm),其重力势能在此不作考虑。则柔性板簧的弹性势能可表示为:


由图2(a)可知,柔性分支Ⅰ由内部运动链和外部运动链构成,因此,其势能为:
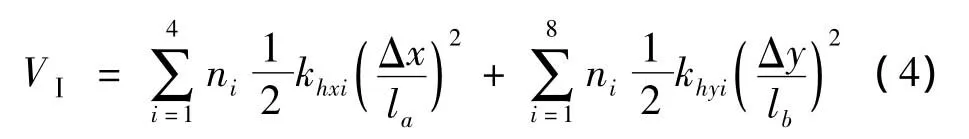
式中:la,lb为刚性杆的长度(见图 2),khx,khy分别为柔性板簧沿x,y向的弯曲刚度。
同理,柔性分支Ⅱ的势能为:
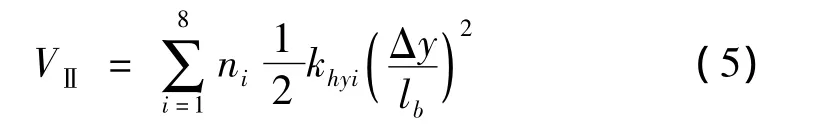
平台的总势能为:

将式(2)和式(6)代入式(1),可得平台的动力学模型:

其中,
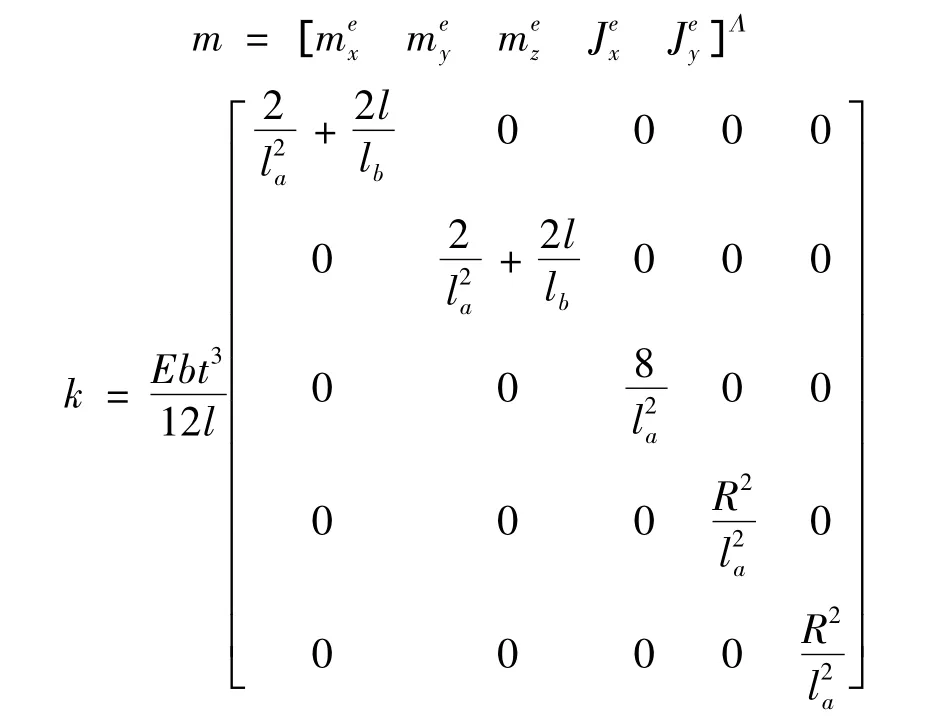
由式(7)可得,平台的固有频率为:

2 模态分析与试验
2.1 ANSYS 模态分析
设计的平台总质量为 1.4 kg,其中mf=0.39 kg,b=10 mm,la=35 mm,lb=30 mm,s=100 mm。为了验证建立的动力学模型是正确的,利用ANSYS软件,对微/纳米传动平台进行模态分析。以四面体单元划分网格,材料选用合金弹簧钢(65Si2Mn),弹性模量E=210 GPa,密度为7 850 kg·m-3,屈服极限为1 176 MPa,泊松比为0.28。完整约束图2所示的安装固定孔,可仿真得平台的前6阶固有频率及模态阵型,如图3所示。

图3 平台的前6阶ANSYS模态阵型Fig.3 First six modal shapes by ANSYS
由图3可知,平台的第1阶模态振型为平台上表面的x,y向扭转和柔性分支1的z向弯曲;第2阶模态振型为平台上表面的x,y向扭转和柔性分支2的y向弯曲;第3阶模态振型为柔性分支1的x向弯曲和柔性分支2的y向弯曲;第4阶模态振型为平台上表面的z向扭转和柔性分支1的x向弯曲、柔性分支2的y向弯曲;第5阶模态振型为柔性分支1和柔性分支2的z向弯曲;第6阶模态振型为柔性分支1的x向扭转柔性分支2的y向扭转。
2.2 模态试验分析
采用模态试验分析方法,对平台进行模态试验,得到其固有频率和阵型,以验证理论动力学模型和ANSYS仿真的正确性。模态试验分析系统的原理图如图4所示,系统主要由LMS SCADAS-Ⅲ可扩展采集前端、BK激振锤、三向加速度传感器、电荷放大器等几部分组成,模态试验装备见图5。
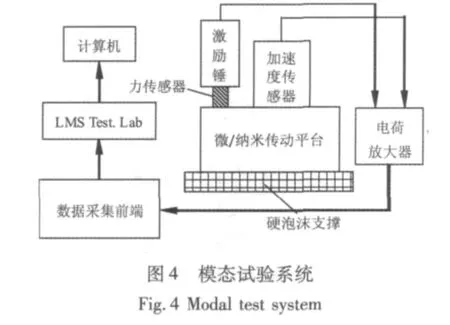

激励锤的激振力信号通过安装在其锤头的力传感器测得,产生的冲击力信号直接接入数据采集前端。响应信号由PCB三向加速度传感器测量得到,将加速度传感器粘在平台的上表面中心点处。模态试验一般有固定支撑和自由-自由支撑两种方式,本试验采用固定支撑方式,利用硬泡沫支撑微/纳米传动平台。在单点重复激振,并对平台的各个测点逐步进行激振,每个测点5次,利用LMS Test.lab分析软件可得测点的平均响应信号,拾取的信号由电荷放大器放大后,接入数据采集前端。
在进行模态试验之前,需合理布置平台的测点,并建立平台的几何模型,以便模态试验的开展及模态参数的识别,且测点要覆盖整个平台,并较好地能反映平台的几何轮廓,再者测点应均匀对称分布且测点数目不宜偏少,建立平台的测点布置及几何模型,如图6所示。锤击法属宽带瞬态激励,用激励锤敲击平台时,当敲击脉冲频率与平台的固有频率相同时,则平台以自身的固有频率作自由振动,振动位移出现峰值,那么,振动位移出现峰值时的激励频率,就是平台的实际固有频率。
根据上述模态试验方法,采用LMS Test.lab分析软件对试验数据进行处理,分别选择平台各阶模态的稳态极点,如图7所示,模态试验得到平台的前6阶阵型如图8所示。由图8可知,平台的各阶模态阵型与ANSYS仿真结果一致,表明模态试验分析方法是正确的,应用该方法对平台识别平台的模态参数是有效的。

图6 平台的测点及几何模型Fig.6 Measured point and geometrical model of the platform

图7 模态试验数据处理Fig.7 Data processing of modal testing
3 平台结构的优化设计
3.1 固有频率分析
由式(7)和式(8)可知,平台的各阶固有频率与柔性板簧的长度l和厚度t的关系,因此,对平台进行结构设计时,在刚性杆几何尺寸一定的情况下,根据建立的动力学模型,可预估和调整平台的带宽,通过调整柔性板簧的长度和厚度,消除平台的固有频率与PZT工作频率的耦合,可避免产生共振,减小柔性机构的残余振动,以提高平台的稳定性、传动精度等动态特性。
由式(8)可知,平台的质量一定的情况下,平台的固有频率f主要受柔性板簧厚度和长度的影响,以第1阶固有频率f1为例,取不同的t,l值,f1随t,l的变化如图9所示。由图可知,柔性板簧厚度t对f1的影响明显,而长度l对f1的影响不大,且f1随着厚度t的增大而非线性增大,随长度l的增大而减小。因此,调整柔性板簧的厚度和长度,提高平台的固有频率时,应首先确定需调整的柔性板簧的几何特征参数,若f1值需大幅度的调整时,应先调整参数t,后调整参数l。
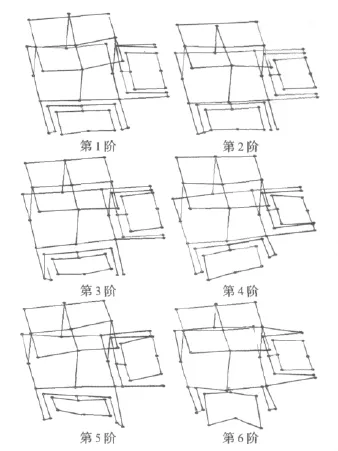
图8 模态试验得到的平台前6阶模态阵型Fig.8 First six modal shapes by modal testing

图 9 f1与 t,l的关系Fig.9 Relationship betweenf1andt,l
3.2 结构优化设计
根据控制理论可知,平台的稳态时间与其固有频率成反比,为了提高平台响应速度和传动精度,应尽可能地提高平台的固有频率,以缩短稳态时间。要评价平台结构设计的合理性,必须使压电陶瓷的工作频率与平台的固有频率完全避开,由于目前平台使用的压电陶瓷的工作频率一般在0~150 Hz范围内,因此,为了避免共振及残余振动,平台的固有频率应该大于150 Hz,而模态试验分析得到的平台前2阶固有频率,与压电陶瓷的工作频率产生耦合,显然,需对平台的结构的进行优化设计,即增大柔性板簧的厚度或减小其长度。
根据式(8)的理论分析,可建立目标函数:

其中,x1,x2分别代表柔性板簧的厚度t和长度l,为了消除平台第1阶固有频率与压电陶瓷的工作频率的耦合,则可建立优化目标:
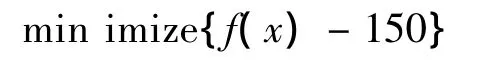
约束条件为:
(1)t值越大,平台的刚性越强,对压电陶瓷的驱动力要求越大,但t值越小,线切割加工难度增大,限定0.2 mm≤t≤2 mm,则:
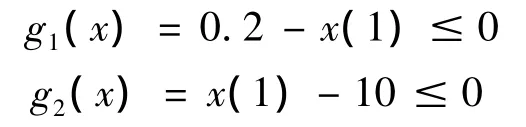
(2)随着l的减小,平台的固有频率增大,但为了保证平台的柔性变形,l的值不宜过小,同时,受到几何空间的约束,限定2 mm≤l≤15 mm,则:
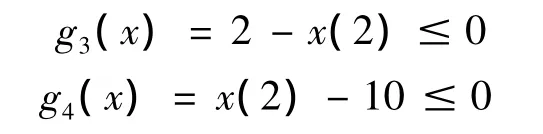
(3)为了保证固有频率完全消除耦合,取一定的安全系数,平台第1阶应大于200 Hz,则:

在Matlab中建立优化模型,对参数l和t进行求解,优化结果为:x(1)=0.96 mm;x(2)=7.54 mm。为了降低加工制造的难度,柔性板簧的厚度和长度取整数,厚度由0.8 mm 增大为1.0 mm,长度由8.0 mm 减小为6.0 mm,得到优化后的平台Ⅱ。同样应用有限元和模态试验方法对其进行分析,ANSYS仿真结果如图10所示。

图10 平台Ⅱ的前6阶模态阵型Fig.10 First six modal shapes of the platform-Ⅱby ANSYS
由图10可知,平台Ⅱ的各阶模态阵型与优化前一样,表明改变柔性板簧的厚度和长度对平台的阵型无影响,只改变平台的固有频率值。模态试验识别出优化前、后平台的前6阶固有频率和阻尼比,如表1所示。优化前、后平台的固有频率对比如图11所示,由图可知,模态试验得到的固有频率,与ANSYS分析、理论分析结果一致,通过对比分析,三者之间的最大误差为9.44%,主要原因为:① 平台的结构尺寸较小(120 mm×120 mm×60 mm),激励锤敲击测点的位置与理想位置有一定的偏差;②平台线切割加工的局部高温导致平台的刚性增强;③根据柔顺机构学推导的柔性板簧的弯曲刚度kh,与实际值之间的误差在1%以内[16],由于忽略了柔性板簧的质量不计,导致模态试验的固有频率比理论模型值稍大。

表1 优化前、后平台的模态频率和阻尼比对比Tab.1 Comparison on natural frequencies,damping ratio between before and after optimization

图11 优化前、后平台的固有频率对比Fig.11 Comparison on natural frequencies of the platform between before and after optimization
同时,对比平台Ⅰ和平台Ⅱ,平台Ⅱ的前6阶ANSYS和模态试验的固有频率大于150 Hz,可避免与PZT的工作频率的耦合。同时,平台Ⅱ的各阶固有频率值比平台Ⅰ对应的固有频率大,可知其随柔性板簧厚度、长度的变化规律与理论分析一致,表明理论动力学建模是正确的,因此,通过调整柔性板簧的几何参数和模态试验分析,优化平台的动态特性是可行的,模态试验分析结果是有效的,为平台的结构优化设计提供了理论和试验依据。
4 结论
(1)通过建立平台的动力学模型,分析了平台固有频率与柔性板簧厚度、长度的相互关系,即厚度越大,长度越小,固有频率越大,为平台带宽的估计、压电陶瓷的选型和结构优化提供理论依据。
(2)以平台固有频率为优化目标,确立了平台的优化模型,并建立了模态试验系统与分析方法,对优化前、后的平台进行了模态试验,识别出的平台的模态参数与理论建模、有限元仿真结果是一致的。
(3)对比分析理论分析、ANSYS仿真和模态试验,结果表明三者的误差不大,说明动力学模型和模态试验方法是正确的。优化前、后平台的模态试验结果,验证了建立的优化模型是有效的,即增大柔性板簧的厚度或减小其长度,提高平台动态性能的方法是可行的。
[1] Zhang D Y,Takahito O,Esashi M,et al.Piezo-actuatorintegrated monolithic micro-stage with six degrees of freedom[J].Sensors and Actuators,2005,122:301-306.
[2]Chu C L,Fan S H.A novel long-travel piezoelectric-driven linear nano-positioning stage[J].Precision Engineering,2006,30:85-95.
[3]Kim D M,Kang D W,Shim J Y,et al.Optimal design of a flexure hinge-based XYZ atomic force microscopy scanner for minimizing abbe errors[J]. Review of Scientific Instruments,2005,76(7):0737061-0737067.
[4]马 立,荣伟彬,孙立宁,等.面向光学精密装配的微操作机器人[J].机械工程学报,2009,45(2):280-287.
[5] Mukhopadhyay D,Dong J Y,Eakkachai P W,et al.A SOIMEMS-based 3-DOF planar parallel-kinematics nanopositioning stage[J].Sensors and Actuators A:Physical,2008,147(1):340-351.
[6] Yuen K Y,Sumeet S A,Moheiman S O,et al.Design,analysis and control of a fast nano-positioning stage[J].Proceedings of the 2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2008:451-456.
[7] Kim J H,Kim S H,Kwak Y K,et al.Development and optimization of 3-D bridge-type hinge mechanisms[J].Sensors and Actuators,2004,116:530-538.
[8]Yu Y Q,Howell L L,Lusk C P,et al.Dynamic modeling of compliant mechanisms based on thepseudo-rigid-body model[J].Journal of Mechanical Design,2005,127(4):760-765.
[9] Tang X Y,Chen I M,Li Q,et al.Design and nonlinear modeling ofa large-displacementXYZ flexure parallel mechanism with decoupled kinematic structure[J].Scientific Instruments,2006,77(11):11510101-11510111.
[10]林 超,俞松松,程 凯,等.大行程5-DOF微纳传动平台的设计及特性分析[J].中国机械工程,2010,21(22):2679-2684.
[11]赵兴玉,冯晓梅,武一民,等.面向制造的高速精密定位平台的动力学仿真和结构设计[J].机械工程学报,2006,42(8):114-118.
[12]李 娟,刘延杰,孙立宁,等.新型2-DOF高加速定位平台的动态性能[J].光学精密工程,2008,16(5):581-585.
[13]李海虹,杨志永.一类二自由度并联机器人的动力学分析[J].天津大学学报,2010,43(4):322-328.
[14]刘 军,高建立,穆桂脂,等.改进锤击法试验模态分析技术的研究[J].振动与冲击,2009,28(3):174-178.
[15] Dong J Y,Yao Q,Placid M F,et al.Dynamics,control and performance analysis of a novel parallel-kinematics mechanism for integrated,multi-axis nano-positioning[J].Precision Engineering,2008,32:20-33.
[16] Howell L L.Compliant mechanisms[M].New York:Wiley Interscience,2001.

