基于离散小波变换和Kalman滤波的直升机主减智能状态预测

刘立生 ，杨宇航

(1.南京理工大学 自动化学院，南京 210094;2.总参谋部陆航研究所 可靠性室，北京 101121)

直升机主减具有传动效率高、结构紧凑等特点，起减速、转向及并车的作用。它将一台或多台高转速小扭矩的发动机功率变成低转速、大扭矩的功率传递给旋翼轴，并按转速和扭矩的需要将功率传递给旋翼、尾桨及各个附件，以保证直升机正常工作。作为旋转机械设备中的一种，主减常见故障类型有机器运行失稳、发生异常振动和噪声、转速发生变化等。Land［1］对HUMS(Healthy and Usage Monitoring Systems)进行研究;Samuel等［2］提出CBM+项目。这些项目的共同点是都对主减的状态进行监控，从而减少了使用与保障(O＆S)费用，提高了直升机的安全性和维修效率。

振动信号常被用来对机械的故障进行诊断［3-4］，利用小波包变换［5-6］或者离散小波变换［7-10］对振动信号进行分解是两种常用方法。在进行小波变换时，小波的选择是关键，选择不同的小波可能会得到不同的结果，Rafiee等［11］比较了324 种母小波，发现“db44”与振动信号最相似，分解效果最好。大量的研究是针对故障检测进行的，而对故障进行预测的研究则相对比较少，文献［12］对预测的方法进行了总结，包括五种方法:基于物理模型、人工神经网络、先验知识(专家系统、模糊系统)、统计方法(趋势推断、ARMA模型)以及随机情况(Kalman滤波、Markov模型、Bayesian网络、可靠性函数)。现实生活中设备受外界的干扰是随机的，故对随机情况进行研究更具有意义。Kalman滤波［13-17］通过一种算法排除可能的随机干扰，提高检测精度，能够很好地对数据进行预测，广泛应用于机器人导航、控制、传感器数据融合以及军事方面的雷达系统以及导弹追踪等。

本文研究了离散小波变换、Kalman滤波以及Elman神经网络组成的智能状态预测系统。文中首先阐述了离散小波变换、Parseval定理、Kalman滤波以及Elman神经网络等理论知识，在文献［13］Kalman预测算法的基础上提出了一种新的Kalman滤波预测算法，接着给出了主减智能状态预测系统的预测流程图，然后以某型直升机主减上8路振动传感器采集的振动数据为例，去噪、分解，利用Parseval定理提取各层能量，分别使用这两种Kalman滤波算法对各路传感器各个时刻的特征向量进行预测，并用Elman神经网络对预测值进行诊断，最终得出:本文提出的算法组成的智能状态预测系统能够更好地对故障进行预测。

1 基于离散小波变换的特征提取

函数ψ(t)∈L2(R)，其 Fourier变换(ω)满足允许条件，则称ψ(t)为一个基本小波或者母小波(mother wavelet)，将母小波经过缩放和平移之后，就可以得到小波序列(a，b∈R，a≠0)。给定基本小波函数ψ(t)，信号f(t)的连续小波变换为:

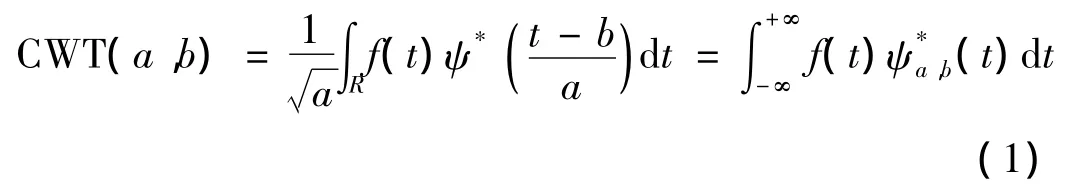
其中:a为尺度参数;b为平移参数。

对尺度参数a和平移参数b进行离散化处理，则离散小波变换为:

式中:a=2-j，b=n2-j。

离散小波变换可以实现多分辨率分析，它将信号分解为近似部分cAj小波系数和细节部分cDj小波系数，接着对近似部分进一步的分解，如此进行迭代，其分解如图1所示，其J层分解表示为:

图1 离散小波变换Fig.1 Discrete wavelet transform

离散小波变换各层能量的提取采用Parseval定理［18］:

式中:x(t)是时域信号，x(f)是离散信号的Fourier变换，N是采样周期。把式(4)代入式(3)得:

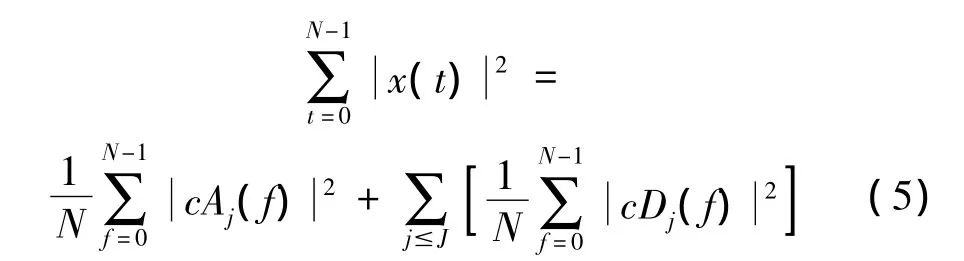
2 Kalman滤波

Kalman滤波是以最小均方误差估计为最佳准则来寻求一套递推估计的算法，其基本思想是:采用信号与噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值，用状态方程和递推方法来估计非平稳随机信号的波形，求出现时刻的估计值。

考虑到直升机主减振动信号的特点，假设其状态模型:

观测模型:

式中:X(k)=［x(k)(k)］T，x(k)是k时刻的值(k)是x(k)在k时刻的变化率，Γ=［T2/2T］T，T为观测周期，Z(k)是k时刻的测量值，H=［10］。w(k)和v(k)分别表示过程和测量的噪声，假设为高斯白噪声，协方差分别为Q，R。

定义:

(k|k-1):由k-1时刻的值估计(k);

P(k| k-1)k|k-1)对应的估计误差协方差;

(k|k):k时刻的最优化估算值;

P(k| k)(k|k)对应的估计误差协方差;

对目标进行Kalman预测具体的流程如图2，实际中通常无法得到目标的初始值，常利用其前两个观测值建立初始估计，即:

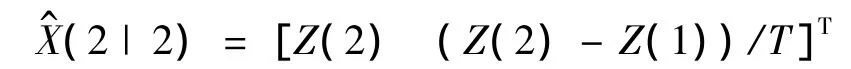
进而得到初始估计的估计误差:

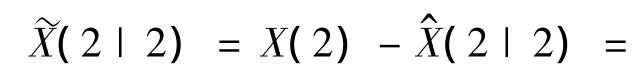
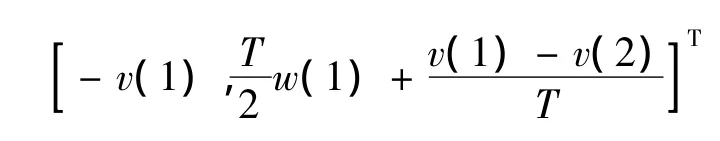
从而得到初始估计误差协方差:

图2 参数预测流程Fig.2 The flowchart of parameter estimation

在获得变化率后，预测值使用得到，预测值有两种算法:

(1)由初始两个观测值Z(1)，Z(2)，利用Kalman滤波求取不同时刻的变化率，获得各时刻预测值［13］。

(2)由初始两个观测值Z(1)，Z(2)预测下一时刻的值(3)，用Z(2)与(3)构成新的观测值，预测下一时刻值(4)，再用(3)与(4)构成新的观测值，对下一时刻进行预测，如此反复迭代，从而获得所有时刻的预测值，该算法是本文提出的方法。

为了简洁起见，用“A”表示文献［13］的算法，“B”表示本文的算法。

3 Elman神经网络

Elman神经网络由Elman提出，该模型在前馈网络的隐含层中增加一个承接层，进行一步延时，达到记忆的目的，从而使系统具有适应时变特性的能力，能直接反映系统的动态特性。Elman型回归神经网络的结构如图2，它一般由输入层、隐含层、承接层和输出层组成，，其中承接层也称状态层或上下文层，隐含层的输出通过承接层的延迟与存储，自联到隐含层的输入。这样就使其对历史数据具有敏感性，增加了网络自身处理动态信息的能力，从而达到了动态建模的目的。

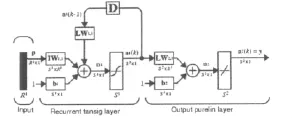
图3 Elman神经网络结构Fig.3 Structure of Elman neural network

4 主减智能状态预测流程图

基于上面介绍的理论，用 DWT、Kalman滤波和Elman神经网络相结合构成直升机主减的智能状态预测系统，其流程图如图4。

其具体过程为:使用振动传感器采集直升机主减上的振动信号，去噪后进行离散小波变换，根据Parseval定理进行特征提取，提取的特征向量进行Kalman滤波由t时刻值预测t+τ时刻的值Xt+τ，最后经Elman神经网络进行诊断。Elman神经网络的诊断流程为:训练数据是每一时刻由实测值获得的特征向量;测试数据是Kalman滤波对应时刻的预测值，预测数据输入训练好的神经网络进行故障诊断，从而实现对直升机主减的状态进行智能预测。

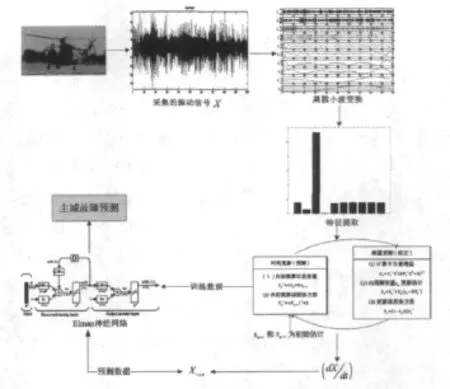
图4 主减智能状态预测算法流程图Fig.4 The workflow of MGB intelligent condition prediction algorithm

5 试验验证

振动传感器监测直升机整个飞行过程中主减上各传动齿轮及轴承处的振动水平，该振动传感器是适用于直升飞机飞行试验的ICP型传感器，其工作温度范围宽，抗干扰能力强，数据采集设备采集8路振动信号，具体检测部位和传感器安装位置如表1所示。

采集直升机地面试车其扭矩为10%时的振动数据，其初始采样频率为20 kHz，由于篇幅关系，以L001为例说明其具体过程。图5为采集的L001信号，横坐标为具体的飞行时刻，纵坐标为振动加速度，共有36 001 264个数据，它包括了一次飞行所有状态下的振动数据，其包含的状态太多，如:爬升、平飞、左侧飞、俯冲、倾斜拉起等纵多飞行状态。

表1 振动监测部位Tab.1 Location for vibration monitoring and measure

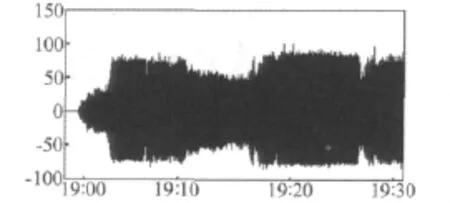
图5 L001采集的原始信号Fig.5 Sample signals of L001

由于数据采集设备配套的FAMOS软件实现不了像小波分析、神经网络、Kalman滤波等复杂算法，但它可以对信号进行重新采样，而Matlab软件一次性处理不了采样频率为20 kHz的大量数据，故本文利用FAMOS软件对各路振动信号进行重新采样，然后利用Matlab软件对新采样后的信号进行分析。通过对各路信号进行重新采样，使得采样频率为原频率的1/20，即1 kHz，然后用语句:data1=Cut(L001，t1，t2)截取时间t1～t2之间的飞行数据，把这些数据拷贝到“.TXT”文档中，供Matlab软件调用。

选择启发式阀值对截取的信号进行去噪处理，对去噪后的信号使用Rafiee［11］中的“db44”进行离散小波分解，分解层数为9，每个传感器得到10个特征向量，由于这10个能量数量级不同，如果直接输入到Kalman滤波和Elman神经网络中，容易产生误判，故需用如下公式对其进行归一化。

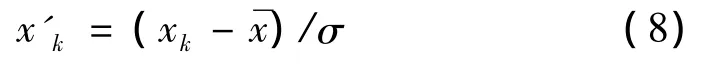
对Kalman滤波，分别采用A，B两种算法对8路传感器每个时刻的各个特征向量进行预测，预测的总时间为30 s，各个时刻的误差采用如下公式:

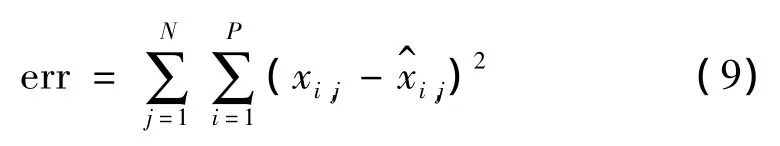
其中，xi，j为第j个传感器的第i个测量值;为第j个传感器的第i个预测值;N为传感器个数。

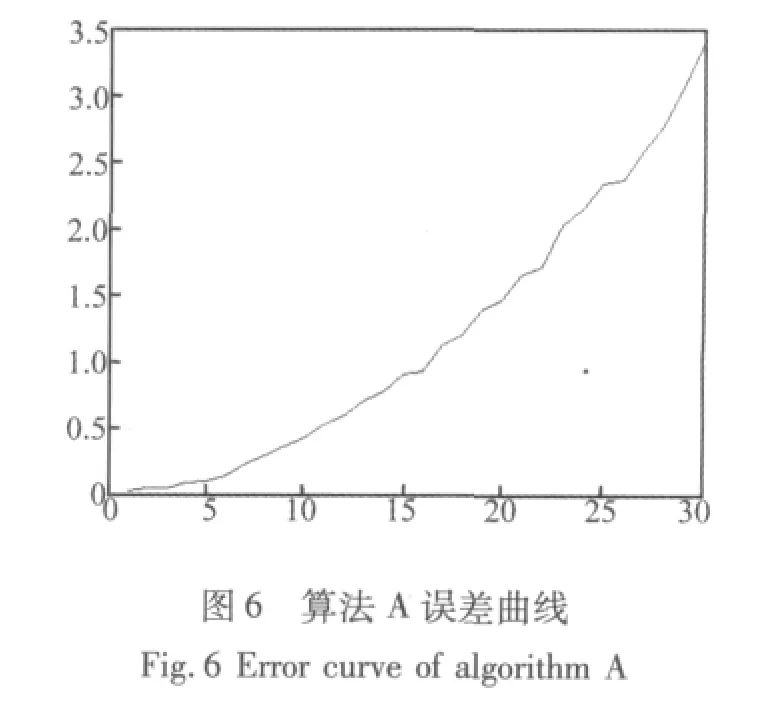
采用A算法时，各时刻误差组成的误差曲线如图6，横坐标为预测时间，纵坐标为误差值，可以看出采用无迭代方法A时，预测时间越长，其对应的误差就越大，而且误差的变化率也在逐渐变大;采用B算法时，各个时刻对应的误差曲线如图7，可以发现随着预测间隔的变大，误差曲线上下波动，而不是单调上升。比较图7和图6，可以清楚地发现，相同时刻算法B的误差值比算法A小得多，部分时刻的具体值如表2，通过表2和对应的图可以知道，虽然图7中波动比较大，但是它的纵坐标很小，从而说明算法B更适合于对各个时刻进行预测，它与实际测量值比较接近。

考虑主减常见的五种故障状态:健康、运动失稳、异常振动、噪声、转速变化，分别用(1 0 0 0 0);(0 1 0 0 0);(0 0 1 0 0);(0 0 0 1 0);(0 0 0 0 1)表示。

为了研究Elman神经网络各个时刻的逼近精度，选取健康状态下的数据进行训练和测试，未经过Kalman滤波的各个时刻的特征数据用于训练神经网络，经过Kalman滤波后获得的预测值用来对网络进行测试，使用newelm构建两层Elman神经网络，隐含层函数为tansig传递函数，输出层为purelin传递函数，算法A与算法B部分时刻的逼近情况如表3所示，这里的逼近精度是相对于各个具体时刻的实际测量值而言的。

表2 不同预测时刻的误差值Tab.2 Error value at different prediction horizons

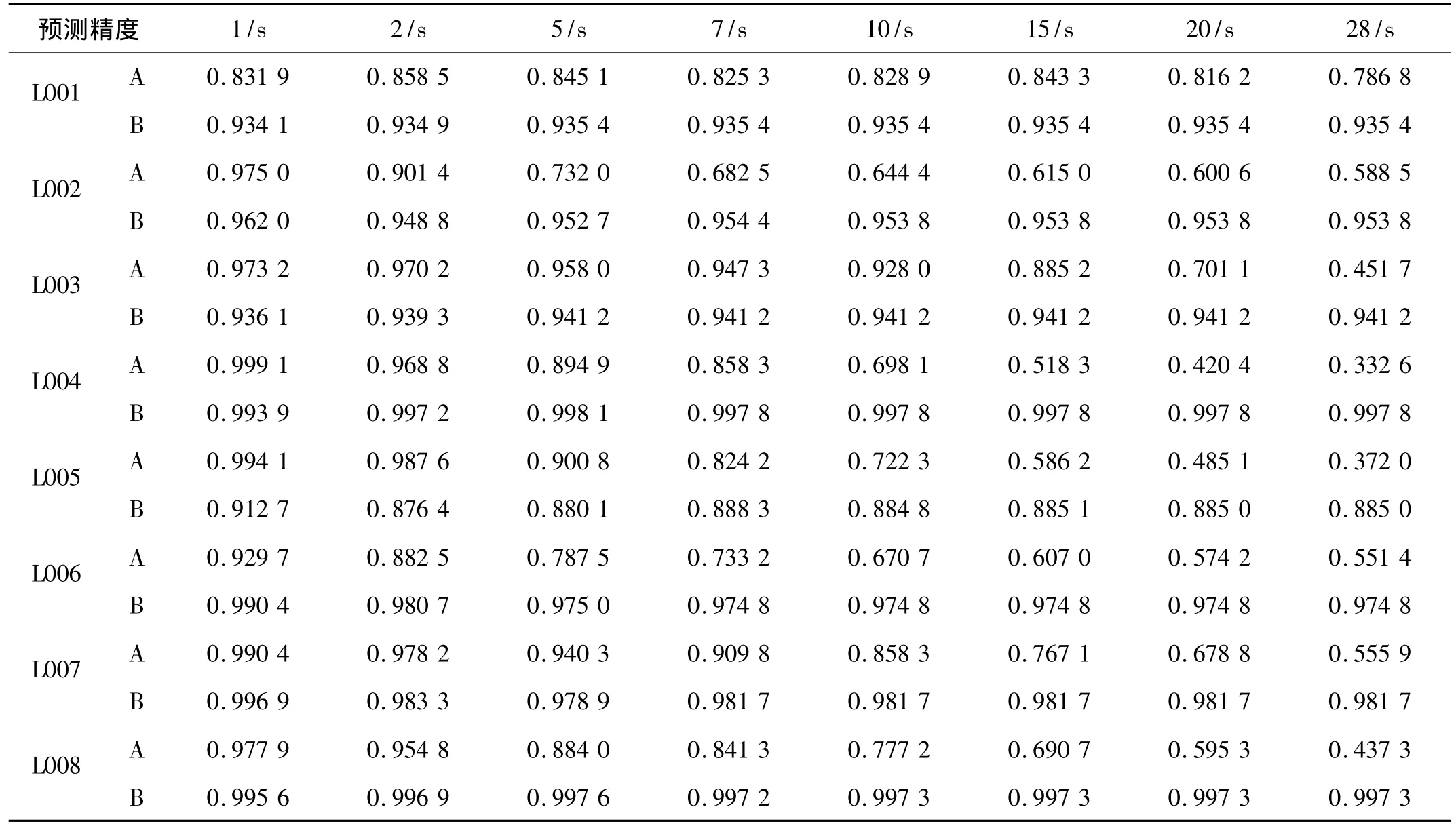
表3 不同预测时刻神经网络的逼近情况Tab.3 The approach accuracies of neural network at different prediction horizons

从上表可以看出，随着预测时间的变大，算法A逼近精度在不断地下降，如L008传感器中，逼近精度在1 s时为 0.977 9，5 s时为 0.884 0，15 s时为0.690 7，28 s时为0.437 3;而 B 算法逼近精度相对都比较高，并且我们发现，随着时间的推移，其相对逼近精度稳定在了一个值上。这进一步说明本文提出的算法更适合用于直升机主减智能状态预测系统的构建。

6 结论

直升机主减是传动装置中结构最复杂、尺寸最大、重量最重的一个部件，它运转的状况直接影响着直升机的安全性和可靠性。针对其故障特点，文中提出了一种基于离散小波变换、Kalman滤波以及Elman神经网络组成的直升机主减智能状态预测系统，通过理论分析和实验验证得到如下结论:

(1)离散小波变换中，母小波选择“db44”能很好地对信号进行分解，有利于应用Parseval定理对其各层进行特征提取。

(2)本文的 Kalman滤波预测算法更适用于对主减的特征向量进行预测，它能够对8路信号的80个特征向量进行预测，并将各路特征向量的逼近精度稳定在一个比较高的固定值上。

(3)应用DWT、Kalman滤波以及Elman神经网络构建直升机主减的智能状态预测系统是可行的，有效的，它能对主减的状态进行精确的预测，将为未来HUMS、PHM、CBM和CBM+系统的进一步开发提供新的技术参考。

［1］ Land J E.HUMS-the benefits-past，present and future［J］.IEEE，2001，6(s):3083-3094.

［2］ Samuel P D，Pines D J.A review of vibration-based techniques for helicopter transmission diagnostics［J］.Journal of Sound and Vibration，2005，282:475-508.

［3］Blunt D M，Keller J A.Detection of a fatigue crack in a UH-60A planetgearcarrierusing vibration analysis［J］.Mechanical Systems and Signal Processing，2006，20:2095-2111.

［4］Rafiee J，Rafiee M A，Tse P W.Application of mother wavelet functionsforautomatic gearand bearing fault diagnosis［J］.Expert Systems with Applications，2010，37:4568-4579.

［5］Wang D Y，Zhang W Z，Zhang J G，et al.Fault bearing identification based on wavelet packet transform technique and artificial neural network［J］.International Conference on System Science，EngineeringDesign and Manufacturing Informatization，2010，2(s):11-14.

［6］ Wu J D，Liu C H.An expert system for fault diagnosis in internal combustion engines using wavelet packet transform and neural network［J］.Expert Systems with Applications，2009，36:4278-4286.

［7］ Wu J D，Liu C H.Investigation of engine fault diagnosis using discrete wavelet transform and neural network ［J］.Expert Systems with Applications，2008，35:1200-1213.

［8］ Saravanan N，Ramachandran K I.Incipient gear box fault diagnosis using discrete wavelet transform(DWT)for feature extraction and classification using artificial neural network(ANN)［J］.Expert Systems with Applications，2010，37:4168-4181.

［9］Wu J D，Huang C K，Chang Y W.Fault diagnosis for internal combustion engines using intake manifold pressure and artificial neural network ［J］.Expert Systems with Applications，2010，37:949-958.

［10］ Wu J D，Kuo J M.An automotive generator fault diagnosis system using discrete wavelet transform and artificial neural network［J］.Expert Systems with Applications，2009，36:9776-9783.

［11］ Rafiee J，Rafiee M A，Prause N，et al.Application of mother wavelet functionsforautomatic gearand bearing fault diagnosis［J］.Expert Systems with Applications，2010，37:4568-4579.

［12］ Sikorska J Z，Hodkiewicz M，Ma L.Prognostic modelling options for remaining useful life estimation by industry［J］.Mechanical Systems and Signal Processing，2011，25:1803-1836.

［13］ Wu S L，Bechhoefer E，He D.A practical regime prediction approach for HUMS applications［J］.American Helicopter Society 63rd Annual Forum，Virginia Beach，VA，2007:1-8.

［14］Peel L，Driven D.Data driven prognostics using a kalman filter ensembleofneuralnetwork models ［J］. International Conference on Prognostics and Helth Management，2008:1-6.

［15］Lall P，Lowe R，Goebel K.Prognostics using kalman-filter models and metrics for risk assessment in BGAs under shock and vibration loads［J］. Electronic Components and Technology Conference，2010:889-901.

［16］ Carr M J， Wang W B. An approximate algorithm for prognostic modelling using condition monitoring information［J］.European Journal of Operational Research，2011，211:90-96.

［17］ Matej G，Dani J，Pavle B，et al.Model-based prognostics of gearhealth using stochastic dynamicalmodels ［J］.Mechanical Systems and Signal Processing，2010，25(2):537-548.

［18］ GaingZ L. Wavelet-basedneuralnetworkforpower disturbance recognition and classification ［J］. IEEE Transactions on Power Delivery，2004，19(4):1560-1568.