金属拉伸件拉伸过程微裂纹AE信号特征参数的优化及状态识别

骆志高，范祥伟，陈 强

（江苏大学 机械工程学院，江苏 镇江 212013）

拉伸是一种高效、节能、高利用率的加工方法，随着现代社会对拉伸加工产品的需求越来越大以及竞争的加剧，人们对拉伸件的质量提出了更高的要求。由于拉伸过程中很容易产生微小裂纹，这些微小裂纹很难被发现且难以得到控制，经常给制件带来潜在的威胁，也一直是企业棘手的技术难题。因此，对拉伸件成型过程质量的在线检测的研究显得尤为重要。本文通过声发射技术在拉伸模具中的应用，解决了对拉伸件成型时产生的微小裂纹的动态监测，实现对金属拉伸件成型质量状态的识别。声发射（Acoustic Emission简称AE），由外部条件的变化引起物体或结构某一局部或某些部分变得不稳定并迅速释放出能量且释放出某些频率的声波［1］。由于声发射信号本身具有不确定性、非平稳性、突发性等特点［2］，使得声发射波形信号处理成为声发射技术中的难点和瓶颈。金属拉伸过程中，声发射提取到的AE信号很难反映实际物理状态的信号参数［3］。本文针对AE特征参数的特点，利用遗传算法［4］对特征参数进行优化，得到最优特征参数之后，选用马氏距离判别法［5］对拉伸件质量状态进行识别。

1 最优特征参数的提取

最佳特征参数提取法包括特征参数的提取和特征参数的优化两个部分，首先对采集到的AE信号进行局域波分解之后提取各IMF的能量值作为初始特征参数，然后基于遗传算法对这些初始特征参数重组优化后得到一个最优特征参数。

1.1 初始特征参数的提取

由于声发射信号本身具有不确定性、非平稳性、突发性等特点，使得声发射波形信号处理成为声发射技术中的难点和瓶颈。局域波法［6］被提出后，经验证在很多方面都优于其它的信号处理方法。局域波法包括两个过程：局域波分解和局域波时频谱。局域波分解方法基于信号的局部特征时间尺度，能把复杂的信号函数分解为有限的本征模函数之和，每一个IMF所包含的频率成分不仅与分析频率有关而且最重要的是随信号本身变化而变化，能突出信号的局部特征，对其进行分析可以更准确有效地把握其中的裂纹特征信息。因此，局域波分解方法是自适应的信号处理方法，非常适合于非线性和非平稳过程，具有很高信噪比。当裂纹声发射信号产生时，声发射信号各频带的能量会发生变化，在各频带信号的能量中包含了丰富的信息，因而可提取各IMF能量作为特征参数来识别裂纹特征，其步骤如下：

（1）对原始采样信号进行EMD（Empirical Mode Decomposition）分解［7］，得到n个IMF分量以及一个趋势项。考虑到故障特征信息主要集中在高频段，故选取包含主要故障信息的前k个IMF分量。

（2）求出各个IMF分量的能量ei。

（3）取前k个IMF的能量作为初始特征参数来构造特征向量T。

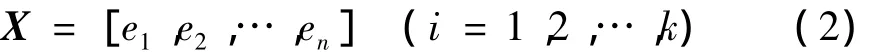
当能量较大时，ei通常是一个较大的数值，在分析时会带来一些不便，可根据式（3）和式（4）对特征向量X进行归一化处理，得到归一化后的特征向量T。

对所采集的每一组4个通道的AE信号在Matlab中进行了局域波分解，提取前k阶IMF分量的能量组成初始特征向量，而各个信号的局域波分解得到的都是8阶以上的分量，所以这里取k=8，即只需求取前8阶IMF的能量组成初始特征向量。

假设每个信号在4个声发射通道均有采集，所以对于每个AE信号我们取4个声发射通道平均能量值作为初始特征参数，根据公式（3）和公式（4），下面给出正常AE信号x1正常和裂纹AE信号y1的数据结果，其余信号依同法可求。

2 实验部分

2.1 试验系统的主要构成

实验系统主要由液压机、拉伸模以及声发射检测系统组成，主要包括：三维输送装备有限公司的350T智能式压力加载机；畚斗拉伸模；鹏翔科技的PXR15谐振式声发射传感器；PXPAIV型声发射前置放大器，50钢等。实验系统的示意图如下：

图1 试验系统原理图Fig.1 Schematic diagram of experiment

2.2 试验过程

2.2.1 主要步骤

（1）构建实验系统，主要由液压机、拉伸模及声发射仪等组成，对整个系统进行调试，分析噪声、测试断铅信号、安装及布置传感器等；

（2）调整液压机的运行速度、模具压边力等参数，以分别采集到拉伸件正常状态及裂纹状态下的AE信号；

（3）对采集到的AE信号进行数据预处理，即把各个AE信号进行局域波分解。

2.2.2 实验参数设置

（1）声发射传感器主要参数：频率带宽：100～300 kHz；灵敏度＞65 dB；谐振频率：150 kHz；使用温度范围：-20～80℃；尺寸：φ18×17 mm。

（2）前置放大器主要参数：频率带宽：15 kHz～1.5 MHz；增益：34/40 dB；噪声：2.8 μVRMS；使用温度范围：-30～80℃；电源功耗：28 V/30 mA；主要尺寸：90×35×30 mm。

（3）采集卡主要参数：声发射输入通道数：4通道/卡；输入电阻：40 Ω；信号带宽：5 kHz～4 MHz；采样分辨率：12字节；采样速度：20 MSps/S；噪声最小阀值：28 dB；最大信号幅度：100 dB；通道隔离度：≥90 dB

2.2.3 数据的采集

图2 拉伸件正常状态下的AE信号x1的波形图（CH1-CH4）Fig.2 The oscillogram of x1（CH1-CH4）for normal state

本次实验分别采集了22组正常状态的AE信号以及22组裂纹状态的AE信号，分别记为x1，x2，…，x22和y1，y2，…，y22。如图2所示是拉伸件正常状态时四个通道所采集到的AE信号x1波形图，图3所示是拉伸件裂纹状态时四个通道所采集到的 AE信号y1的波形图。

图3 拉伸件裂纹状态下的AE信号y1的波形图（CH-CH4）Fig.3 The oscillogram of x1（CH1-CH4）for crack state

3 实验数据处理

3.1 数据预处理

将已经采集到了22组正常状态的AE信号数据以及22组裂纹状态的AE信号数据输出至Excel表，通过Matlab调用函数将Excel中的数据导入进而实现局域波分解，提取各imf的能量作为初始特征参数。

由于采集到的各个AE信号均是一种典型的非平稳信号，而局域波分解方法是自适应的信号处理方法，非常适合于非线性和非平稳过程，故首先要对采集到的各个AE信号进行局域波分解，以利于进一步的数据分析及处理。本文对AE信号的局域波分解，是在Grilling的算法基础上实现的，部分程序代码如下：m=xlsread（‘00.xls’，‘sheet1’，‘A1：A2560’）；

受篇幅所限，在这里只给出其中第一通道采集的正常状态的AE信号x1和第一通道采集的裂纹状态下的AE信号y1的局域波分解的结果，如图4和图5所示，从图中可以看出，AE信号x1（CH1）经局域波分解之后得到9个本征模函数分量和一个趋势项，AE信号y1（CH1）经局域波分解之后得到9个本征模函数分量和一个趋势项。

对于正常状态的AE信号x1其数据结果如表1所示。取4个声发射通道的平均值可得AE信号x1的特征参数：

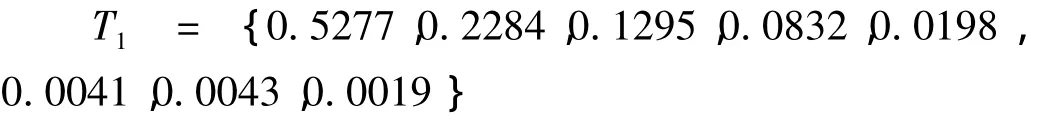
对于裂纹状态的AE信号y2其数据结果如表2所示。

表1 正常AE信号x1（CH1～CH4）的特征参数Tab.1 Characteristic parameters of x1（CH1 ～CH4）for normal state of AE signal

表2 裂纹AE信号y1（CH1～CH4）的特征参数Tab.2 Characteristic parameters of y1（CH1 ～CH4）for crack state of AE signal

取4个声发射通道的平均值可得AE信号y1的特征参数：

3.2 初始特征参数的重组优化

对前面得到的初始特征参数基于遗传算法进行优化重组，以生成一个识别能力优良的最优特征参数，记为P1、P2它们分别表示正常状态和裂纹状态的AE信号的最优特征参数。在本文中进行遗传操作其GA的参数分别取遗传因子数300，世代交替数1 000，淘汰率0.2，树形图的深度为5，对于正常AE信号x1、裂纹信号y1进行遗传操作可得到其最优特征参数的表达式为：

显然，对于其它信号进行同样操作也可以得到其最优特征参数的表达式，受篇幅所限，这里只给出其中一组正常AE信号x1、裂纹信号y1的初始特征参数经遗传算法优化重组后所的到的最优特征参数的表达式，其余信号的不再给出。

3.3 拉伸件成型时裂纹状态的识别

在提取到最优特征参数之后，最后一步就是对拉伸件质量状态的识别，这是一个模式识别的问题。本文使用的是较为简单的马氏距离判别法来进行模式识别，之所以没有采用神经网络、支持向量机等较为复杂的模式识别方法，是因为只有一个特征参数值，同时也是因为马氏距离法在其计算效率上的优势。

3.3.1 马氏距离判别法

本文分别对拉伸件的两种状态进行识别，即正常状态和裂纹状态。前面我们经初始特征参数的提取和优化之后得到了一个最优特征参数，再分别计算出各个最优特征参数的值，我们把训练样本的特征值记为Pi，检验样本的特征值记为Px，求出同类状态下所有训练样本的特征值Pi的平均值和方差 var（Pi），这里把特征值Pi的平均值称为标准特征值，i=1，2分别对应拉伸件的正常状态和裂纹状态。可以通过下式来计算Px和拉伸件质量的两个状态下的标准特征值之间的马氏距离：

然后比较D1和D2的大小，取其中最小判别距离对应的状态为测试样本的状态类型，也即：如果D1＜D2，则拉伸件的质量是正常状态；如果D1＞D2，则拉伸件的质量处于裂纹状态。

3.3.2 识别结果

对于所采集到的44组AE信号，将其中的11组AE 信号x1，x2，…，x11以及 11 组 AE 信号y1，y2，…，y11作为训练样本，其余的22组AE信号作为测试样本。分别求出拉伸件正常状态和裂纹状态下的训练样本的标准特征值和方差 var（Pi），求得的结果如表3所示。

表3 裂纹及正常状态下标准特征值和方差Tab.3 Standard eigenvalue and variance of the cracks and normal states

然后，根据式（7）分别计算出20组测试样本的特征值Px与正常状态下和裂纹状态下的标准特征值之间的距离，并比较比较D1和D2的大小，当D1＜D2时，所测试的样本是正常状态；当D1＞D2时，所测试的样本是裂纹状态。

表4 马氏距离识别结果Tab.4 Results of Mahalanobis Distance Discrimination

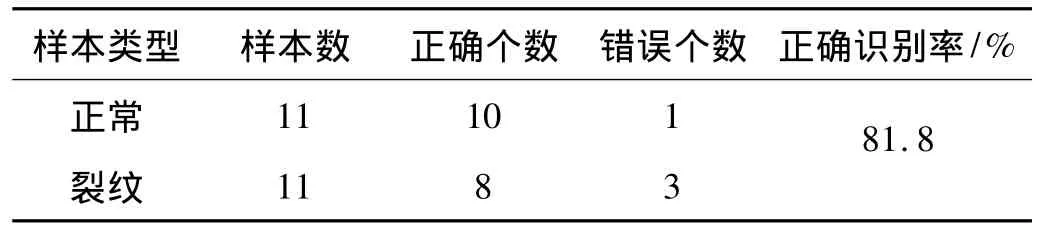
表5 修正前的正确识别率统计Tab.5 Discrimination rate before corrected

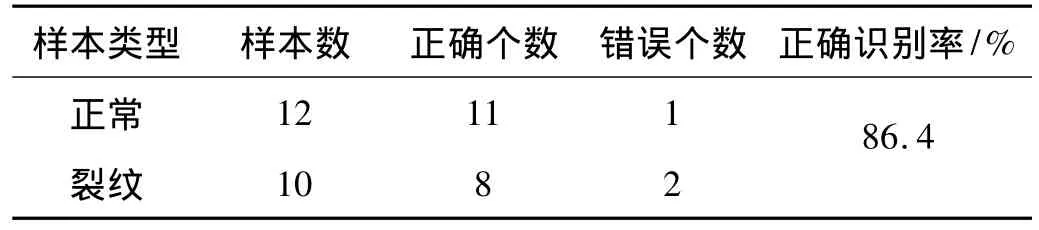
表6 修正后的正确识别率统计Tab.6 Discrimination rate after corrected

表4给出了其中10组测试样本经马氏距离识别的结果，从表中可以看出对于这10组测试样本分析结果与实际完全相符。而对于全部22组测试样本识别的正确率的统计如表5所示，从表中可以看出，对于22组测试样本，有18组样本得到了正确的识别结果，而其它4组样本中，有3组样本的D1和D2的大小相近不能判断，经分析可能是由于在实验时各种干扰因素造成的数据不准确，另1组样本的识别结果是裂纹状态而“实际”状态是“正常”状态，把这组样本所对应的拉伸件去做镜像分析，发现拉伸件内部有肉眼看不到的微裂纹，也即这组样本的识别结果与实际状态相符，那么实际上本次实验对拉伸件的质量状态的正确识别率达到了86.4%（见表6），实验结果说明了该方法可以有效地识别出拉伸件的裂纹AE信号从而判断出拉伸件的质量状态。

4 结论

本文首先将声发射初始特征参数进行提取，得出两组不同的特征向量，再运用遗传算法对AE特征参数进行重组优化，使用简单的马氏距离实现对拉伸件质量状态的识别，由此得到以下结论：

（1）提出了识别指数的概念用于评价特征参数识别两种状态的能力，从理论上推导出其计算公式，并由此来建立遗传算法的适应度函数，按照设定的相应遗传参数对局域波提取的初始能量特征参数进行重组优化能自动生成一个最优特征参数，证明了遗传算法强大的空间寻优搜索能力。

（2）对于采集到的AE信号运用本文的方法得到了一个最优特征参数，使用简单的马氏距离对拉伸件的两种质量状态成功实现了识别，总的识别率达到了85%以上，验证了“最优特征参数提取法”的有效性。

［1］ASTM E1316-1996，Terminology for Nondestructive Examination［S］.U.S.A，1996.

［2］胡昌洋，杨钢锋，黄振峰，等.声发射信号处理和分析技术［J］.无损检测，2002，24（1）：23-28.

［3］骆志高，王 祥，李 举，等.利用声发射信号的特征分析对冲压模具的状态判别［J］.振动与冲击，2008，27（3）：187-189.

［4］ Holland J H.Adaptation in natural and artificial systems［M］.Ann Arbor：The University of Michigan Press，1975.

［5］ Kalpana P，Gunavathi K.A novel implicit parametric fault detection method for analog/mixed signal circuits using wavelets［J］.ICGST-PDCS Journal，2007，7（1）：43-48.

［6］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc.Roy.Soc.Lond.A，1998，454：903-995.

［7］于德介，程军圣，杨 宇.Hilbert能量谱及其在齿轮故障诊断中的应用［J］.湖南大学学报（自然科学版），2003，30（4）：47-50.