橡胶支座与柱串联体系的动力特性分析

杜永峰，林治丹，李 慧

（1.兰州理工大学 防震减灾研究所，兰州 730050；2.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州 730050）

隔震建筑显著的隔震减震效果已在地震中得到了充分验证，使隔震结构在各国得到广泛应用［1］。目前，隔震技术的主要应用为基础隔震，即隔震层设在基础顶面。串联隔震体系是在基础隔震体系的基础上发展而来的复杂结构体系，隔震层设在地下室悬臂柱顶部，如图1、图2所示，其振动特性同时受到隔震层以上的上部结构及下部结构的影响。Gent［2］最早基于Harings理论研究了叠层橡胶支座的力学性能。Ryan等［3-4］在双自由度力学模型的基础上提出了考虑轴向荷载的叠层橡胶支座非线性模型，分析了轴向荷载对于水平刚度的影响。Kelly［5-6］基于梁柱理论，分析了叠层橡胶支座的竖向刚度、水平刚度和拉伸屈曲。周锡元、韩淼等［7-8］在 Gent 和Kelly研究基础上建立了柱串联隔震系统的分析模型 ，推导出柱串联隔震系统的水平刚度计算公式及临界荷载求解公式。马长飞等［9］针对柱顶隔震体系，提出了考虑PΔ效应动力响应的免迭代计算方法，分析了P-Δ效应对柱顶隔震结构的影响。然而，有关串联隔震体系的动力学性能的研究报道较为少见。考虑转动惯量、剪切变形以及轴向力对串联隔震体系固有频率的影响的研究更是少有。对于橡胶隔震支座与柱串联的隔震体系而言，隔震体系的转动惯量、剪切变形以及竖向轴力等将会改变体系的固有频率。

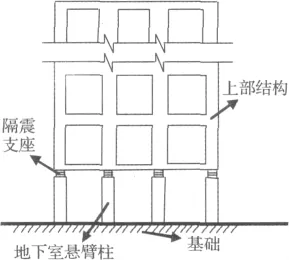
图1 串联隔震结构Fig.1 Serially isolated structure

本研究是在前人分析模型的基础上，推导出串联隔震体系自由振动边值问题的控制方程；其次，导出了频率方程，并采用微分求积单元法［10-12］对方程及边界条件进行离散；最后，数值求解频率方程，得到了相应的固有频率参数，并利用数值结果探讨了轴向力作用下，串联隔震体系动力特性以及支座等效弯曲刚度等对固有频率的影响。这些结果为深入研究串联隔震体系的动力行为提供了基础。

图2 串联隔震体系分析模型Fig.2 Deformation pattern for serially connected isolation

1 串联隔震体系的分析模型

考虑图2所示串联隔震体系总高度为H，上部为叠层橡胶隔震支座，将钢板和橡胶片组成的叠层结构简化为等价的连续均匀柱，同时考虑弯曲变形和剪切变形的影响［13-15］，其 横 截面为Ar、直径为d、等效密度为ρr，修正弯曲弹性模量为Er、剪切模量Gr、横截面惯性矩为Ir。下部为钢筋混凝土柱，且在高度为h处刚性连接隔震支座，其横截面为Ac、等效密度为ρc，弹性模量为Ec、剪切模量Gc、横截面惯性矩为Ic，另一端y=0与基础固结。

图3 串联隔震体系微元段的受力图Fig.3 Differential element

考虑转动惯量和剪切变形对体系的影响，串联隔震体系变形可由轴线挠度w（y，t）和横截面的转角θ（y，t）两个广义位移来表示。微元段的变形示于图3中，其中P为轴力，横截面弯矩和剪力分别为M和Q，θ是弯矩引起的截面转角，γ是剪力引起的剪切角，∂w/∂y为变形后轴线的切线与y轴的夹角，三者之间的关系：θ=∂w/∂y+γ。

2 控制方程和边界条件

考虑弯曲变形时轴力P的二阶效应以及微元段的平动和转动惯性效应，可得串联隔震体系的运动方程为：

本构方程：

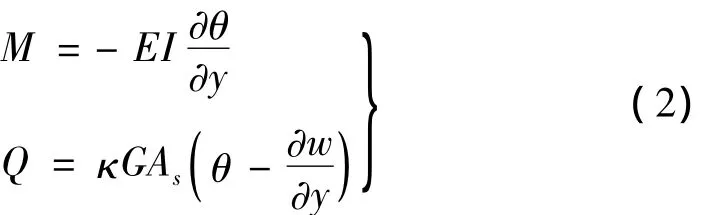
式中：κ为剪切形状因子，与横截面形状和泊松比μ有关。

将式（2）代入式（1）中，可得到考虑轴力作用的串联隔震体系动力运动方程：

引入有限元的概念，把串联隔震体系分为两个单元，变量右上标的表示第e个单元。其中，表示下部钢筋混凝土柱单元表示上部叠层橡胶隔震支座单元。则，记w1（y，t）和θ1（y，t）分别为下部钢筋混凝土柱的横向位移和弯曲引起的横截面转角，而和θ2（y，t）分别为上部叠层橡胶支座的横向位移和弯曲引起的横截面转角。考虑轴向力对串联隔震体系横向振动的影响，则串联隔震体系的运动控制方程为：

而两端的边界条件为：

钢筋混凝土柱与隔震支座存在内部边界条件（协调条件），包括位移协调条件和内力平衡条件：

3 特征方程及其微分求积格式

3.1 特征方程

3.2 无量纲化

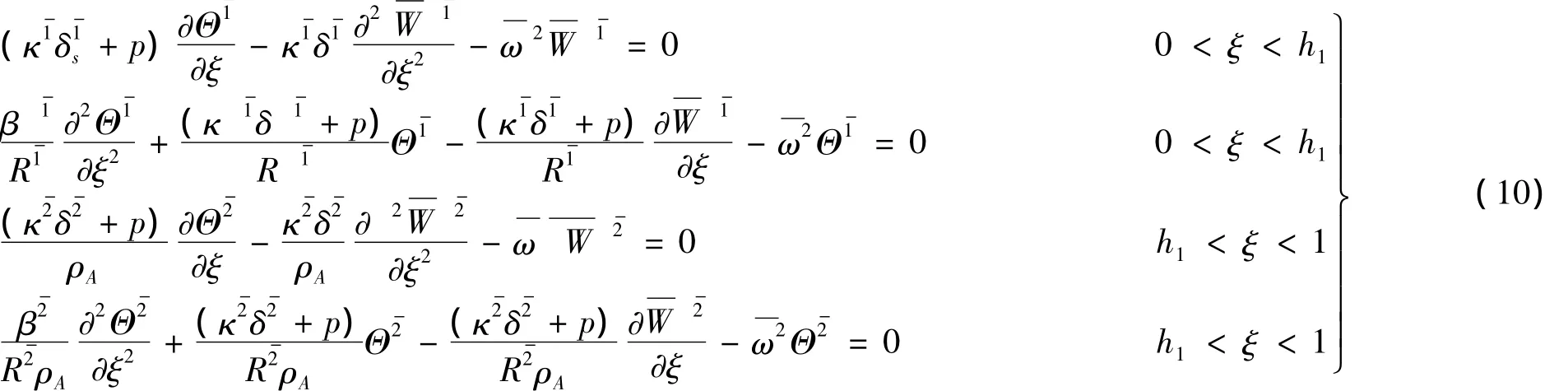
3.3 微分求积格式

微分求积法（Different Quadrature Method）本质上是把函数偏导数在某点的值近似用全域内节点函数值的加权和来表示，并在全域内运用高阶Lagrange多项式逼近域内某一待求连续函数。对于本文研究的串联隔震体系，分别在叠层橡胶支座和悬臂柱两个单元分别运用微分求积法，即微分求积单元法，在y方向各取n个节点，根据微分求积原理［16-17］，将式（10）在［0，1］区间内进行离散，其微分求积形式为：

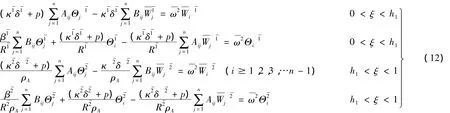
边界条件的微分求积形式为：

式中：Aij，Bij分别表示加权系数，分别由下式确定：

当r=2，3，...，n-1 时，有：

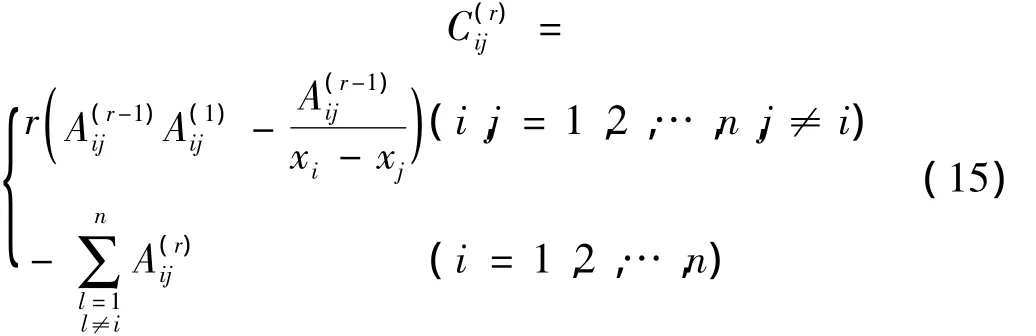
对式（12）采用非均匀的Chebyshev-Gauss-Lobatto节点布置，节点分布形式为：

采用替换法处理边界条件，联立式（12）和式（13）可以得到4n个方程，通过变形可以写成矩阵形式：

式中：［Kee］，［Kei］，［Kie］，［Kii］分别是阶数为（8 ×8），（8×（4n-8）），（（4n-8）×8），（（4n-8）×（4n-8））的矩阵；{Xe}，{Xi}分别为8维和（4n-8）维列向量，且：

式（17）可以变形得到：

式（18）即为体系固有频率的特征方程。

4 数值分析与讨论

考查实际工程中由混凝土强度等级为C30、弹性模量E=3.0e10 Pa、剪切形状因子κ=0.845、截面尺寸为1 050 mm×1 050 mm的地下室悬臂柱和橡胶隔震支座组成的总高为3 m的串联隔震体系。隔震支座剪切形状因子κ=0.899，其它参数见表1。

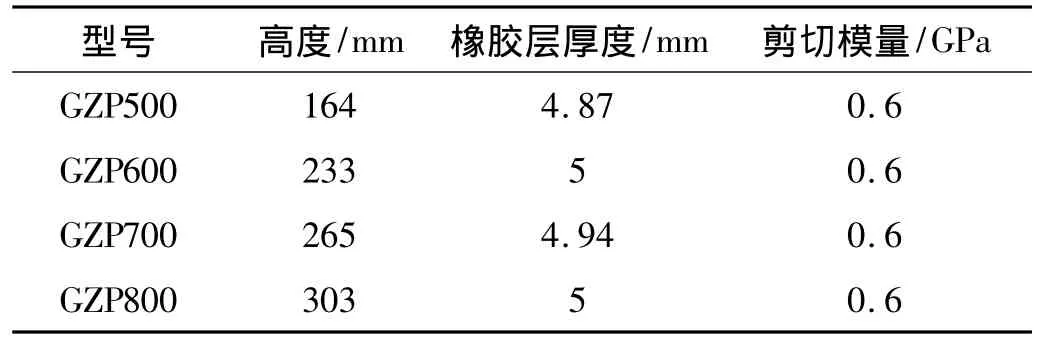
表1 橡胶隔震支座参数Tab.1 Parameters of rubber bearings

数值计算中，取每段的节点数为19，应用微分求积单元法求得串联隔震体系在竖向荷载作用时的前五阶固有频率，列于表2中。

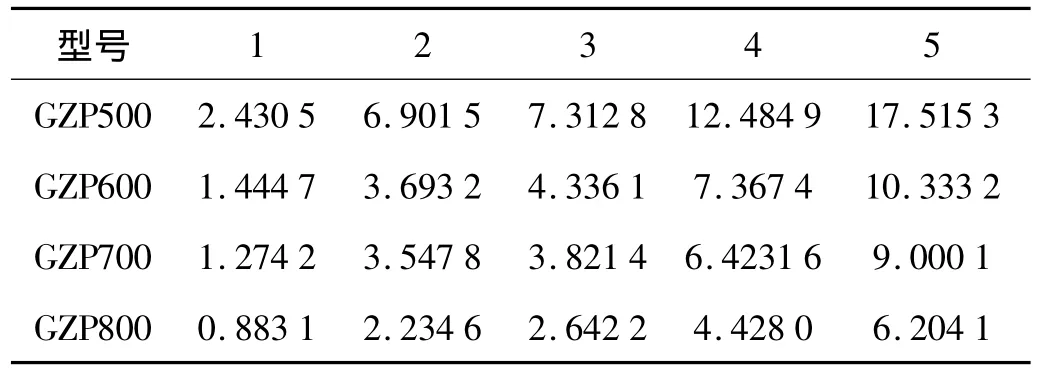
表2 10 MPa竖向荷载作用下前五阶无量纲频率参数Tab.2 Frequency under 10 MPa vertical load

图4给出了GZP500支座的第一阶和第五阶无量纲频率随着无量纲竖向荷载p的变化曲线。从图中可以看出，随着荷载的增加，串联隔震体系的第一阶、第五阶固有频率逐渐降低，当竖向荷载接近体系的临界荷载时，第一阶固有频率趋于零，串联隔震体系发散失稳。而第五阶频率随着荷载p的增加而缓慢减小。

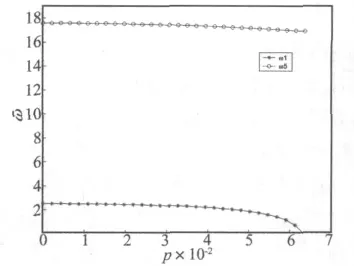
图4 GZP500支座第一阶频率和第五阶频率Fig.4 1stand 5thfrequency-vertical load curve

图5给出了各支座串联隔震体系自由振动基频随荷载p的变化曲线。从图5中可以看出，串联隔震体系的基频随着荷载p的增大而单调减少，当竖向荷载接近体系的临界荷载时，第一频率趋于零，此时GZP600、700、800支座的无量纲临界荷载分别为 0.056 9、0.068 4、0.077 9。在频率平稳下降段，第一频率随着隔震支座型号的增大而降低。图中还反映出随着隔震支座型号的增大，各临界荷载随之增大。同时，在各基频显著下降段处，有明显的交叉现象，各串联隔震体系基频之间的大小关系出现紊乱，而表2仅是频率平稳下降段的一个局部表现，因此图5结果与表2的结果是相符的。

进一步分析不同支座对于串联隔震体系第一阶频率的影响。由文献［1］可知，影响叠层橡胶隔震支座的参数较多，文中仅以叠层橡胶支座等效弯曲刚度EI为宏观参数来分析不同支座型号对于串联隔震体系基频的影响。从图6中可以看出，除p=28 MPa外，在某一定值竖向荷载作用下，串联隔震体系的基频随着支座等效刚度的增加而减少。当竖向荷载为p=28 MPa时曲线出现突变，说明在该荷载作用下GZP500、600支座已经进入基频下降段，而GZP800支座仍处于平稳下降段，因此GZP500支座的串联隔震体系的基频在此情况下出现突变，而GZP800支座的串联隔震体系变化较小，这与图5的结果相符。

将支座截面惯性矩从等效弯曲刚度中单独提取出来。图7给出了不同支座惯性矩对串联隔震体系频率的影响，其变化趋势与等效刚度类似。

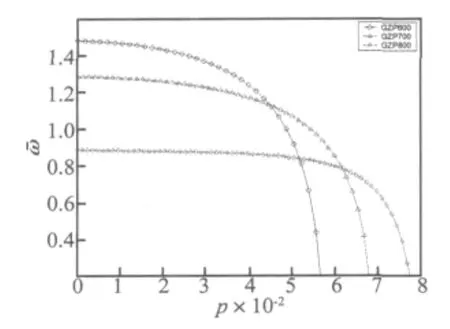
图5 串联隔震体系频率与荷载变化曲线Fig.5 Frequency of serially isolated system-vertical load curve

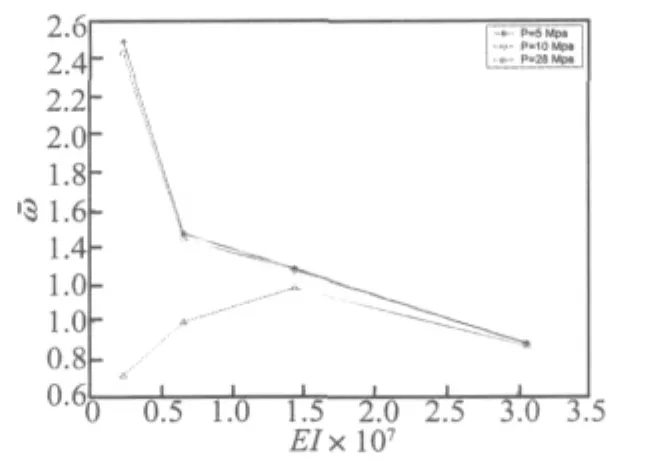
图6 串联隔震体系频率与支座等效弯曲刚度变化曲线Fig.6 Frequency of serially isolated system-equivalent stiffness curve

图7 串联隔震体系频率与惯性矩变化曲线Fig.7 Frequency of serially isolated system-moment of inertia curve

5 结论

本文在前人的研究成果之上确立了串联隔震体系动力分析模型，采用微元段的方法建立了该体系的运动方程，导出了串联隔震体系的控制方程和边界条件，并应用微分求积单元法这一较成熟的数学方法进行数值求解。研究了在竖向荷载作用下串联隔震体系的振动问题。数值结果表明：随着竖向荷载的增加，串联隔震体系的固有频率逐渐降低；当竖向荷载接近体系的临界荷载时，固有频率趋于零；在频率平稳下降段，某一竖向荷载作用下，串联隔震体系的固有频率随着叠层橡胶支座型号的增大而降低，支座等效弯曲刚度对于体系的固有频率也具有同样的影响。

［1］周福霖.工程结构减震控制［M］.北京：地震出版社，1997.

ZHOU Fu-lin.Seismic control of engineering structure［M］.Beijing：Seismological Press，1997.

［2］Gent A N.Elastic stability of rubber compression springs［J］.Journal of Engineering Mechanics，1964，6（4）：318-326.

［3］Koh C G，Kelly J M.A simple mechanical model for electrometric bearings used in base isolation［J］.Journal of Engineering Mechanics，1988，30（12）：933-943.

［4］Ryan K L，Kelly J M，Chopra A K.Nonlinear model for lead-rubber bearings including axial-load effects［J］.Journal of Engineering Mechanics，2005，131（12）：1270-1278.

［5］Kelly J M.Tension buckling in multilayerelastomeric bearings［J］. Journal of Engineering Mechanics，2003，129（12）：1363-1368.

［6］Kelly J M.Earthquake resistant design with rubber［M］.London：Spriger，2nd Ed.，1997.

［7］周锡元，韩 淼，曾德民，等.橡胶支座与R/C柱串联隔震系统水平刚度系数［J］.振动工程学报，1999，12（2）：157-165.

ZHOU Xi-yuan，HAN Miao，ZENG De-min，et al.Horizontal rigidity cofficient of the serial system of rubber bearing with column［J］.Journal of Bibration Engineering，1999，12（2）：157-165.

［8］周锡元，韩 淼，曾德民，等.组合橡胶支座及橡胶支座与住串联系统的水平刚度计算方法［J］.地震工程与工程振动，1999，19（4）：67-75.

ZHOU Xi-yuan， HAN Miao， ZENG De-min， etal.Calculatin method of lateral stiffness of combined rubber bearing and serial system of bearing with columns［J］.Earthquake Engineering and Engineering Vibration，1999，19（4）：67-75.

［9］马长飞，谭 平，张亚辉，等.考虑P-△效应的柱顶隔震结构的动力响应分析［J］.土木工程学报，2010，43：230-234.

MA Chang-fei，TAN Ping，ZHANG Ya-hui，et al.Dynamic responses Anslysis of structures with isolators on the top of the columns considering P - △ effects［J］.China Civil Engineering Journal，2010，43：230-234.

［10］ Wang X，Bert C W.A new approach in applying differential quadrature to static and free vibration analyses of beams and plates［J］.J.Sound and Vibration，1993，162（3）：566-572.

［11］Wang X W，Liu F，Wang X F，Gan L F.New approaches in application of differential quadra-ture method to fourth-order differential equations［J］.Commun.Numer.Meth.Engng，2005，21：61-71.

［12］ Liu G R，Wu T Y.Vibration analysis of beams using the generalized differential quadrature rule and domain decomposition［J］.Journal of Sound and Vibration，2001，246（3）：461-481.

［13］周锡元，韩 淼，曾徳民，等.叠层钢板橡胶垫的稳定性分析与强度验算［J］.建筑科学，1997（6）：13-19.

ZHOU Xi-yuan，HAN Miao，ZENG De-min，et al.Stability analysis and strength checing of laminated rubber bearing［J］.Building Science，1997（6）：13-19.

［14］唐家祥，刘再华.建筑结构基础隔震［M］.武汉：华中理工大学出版社，1993.

［15］ Imbimbo M，Kelly J M.Stability of isolators at large horizontal displacements［J］.Earthquake Spectra，1997，13（3）：415-430.

［16］刘金堂，杨晓东，闻邦椿.基于微分求积法的轴向运动板横向振动分析［J］.振动与冲击，2009，28（3）：178-181.

LIU Ji-tang，YANG Xiao-dong，WEN Bang-chun.Transverse vibration of an axially moving plate based on differential quadrature method［J］.Journal of Vibration and Shock，2009，28（3）：178-181.

［17］李晶晶，胡育佳，程昌钧，等.粘弹性Timoshenko梁非线性动力学行为的微分求积分析［J］.振动与冲击，2010，29（4）：143-145.

LIJing-jing， HU Yu-jia， CHENG Chang-jun， etal.DifferentalQuadrature method for nonlinear dynamical Behavior of a viscoelastic timoshenko beam ［J］.Journal of Vibration and Shock，2010，29（4）：143-145.