接触界面对拉杆组合柔性转子轴承系统的非线性动力特性影响

易 均，刘 恒，刘 意，于 明，王为民

(1.西安交通大学 机械工程学院，西安 710049;2.东方汽轮机有限公司，四川 德阳 618000)

现代燃气轮机、航空发动机等大型动力系统的核心部件均为典型的拉杆柔性组合转子。此类转子的多个独立轮盘间依靠接触界面传递各向作用力，并在拉杆预紧下组合为一体。重量轻、易于装配且具有良好的冷却效果是此类转子的特点，针对高速化、高效化的工业发展，应用前景非常广泛。

目前，针对一般整体转子稳定性的讨论已有很多，如刚性轴的稳定性有文献［1］等，简单Jeffcott柔性转子轴承系统稳定性有文献［2］等，一般柔性转子轴承系统则有文献［3］等。然而拉杆组合转子轮盘间非线性本质的接触效应，导致此类组合转子其结构本质上是不连续的，传统的视作整体转轴的转子处理方式不适用于此类分布式特种转子。针对拉杆组合转子动力特性的研究，饶柱石等［4-5］提出了拉杆组合转子的一般力学模型，王艾伦等［6-8］则进行了计及接触界面的临界转速计算，但是此处非线性动力特性的研究仍然十分有限。

运用文献［9］提出的粗糙机械结合面接触刚度的研究方法，通过计算与真实接触面等条件下的微元模型界面接触刚度并将之进行面积扩展，得到轮盘界面接触刚度;将接触界面处理成无质量均质弹簧［5］，采用哈密顿原理完成了计及接触界面的转子建模，得到了拉杆转子轮盘间界面产生的附加刚度矩阵;而后结合对整体转轴应用计及轴向力的铁木辛格梁轴单元建立的有限元模型，得出了转子轴承系统的动力学方程。最后运用打靶法结合Floquet稳定性分叉理论，对比了计及接触界面前后的系统稳态周期解的稳定性边界和分叉形式，数值结果表明接触界面对不平衡转子动力特性的影响不可忽略。

1 接触界面建模

拉杆组合转子的轮盘是通过拉杆预紧而组合在一起的。其轮盘间接触界面在预紧力作用下发生变形产生作用力而传递轴向力，因此可以将接触界面单独视作一个无质量的面弹簧单元，在对拉杆组合转子建模时，将接触界面作为一个附加弹簧单元的形式添加到系统，如图1所示。

图1 接触界面弹簧替代示意图Fig.1 Contact interface replaced by springs

附加弹簧单元刚度大小即为界面接触刚度，由预紧力大小和接触界面属性(材料，粗糙度，形貌度，波浪度等)决定。在弹性范围内，预紧力越大则其刚度越大;接触界面粗糙度、形貌度和波浪度等都是影响界面接触刚度大小的几何因素，其中粗糙度为研究各种几何因素的基础。此处研究采用的模型其接触界面仅仅计入了粗糙度的影响，对形貌度等其他几何因素影响的研究，需综合粗糙度的影响，并在此基础上进一步深入讨论。实际情况中接触界面形貌度和波浪度对界面刚度的影响均会大于单一的粗糙度的影响，二者导致的接触界面刚度变化对动力特性的影响也会比单一的粗糙度因素更大。

1.1 弹簧单元刚度确定

直接在米级的全尺寸模型中研究微米级的粗糙度对界面刚度的影响，巨大的计算尺度跨越使得此处分析非常困难。本文采用等条件的微元有限元模型分析与宏观尺寸相结合的跨尺度计算方法，从而准确得到轮盘间接触界面刚度，其步骤为:① 计算轮盘间如图1所示A接触界面面积s2，对轮盘接触界面进行受力分析，得到预紧后的真实界面压力P;② 根据文献［9］方法建立在压力P作用下的面积为s1、与轮盘接触面等条件的微观有限元模型如图2所示，对此模型进行应力应变分析并提取该微元法向接触刚度k;③ 由于线性面弹簧与弹簧面积成正比，轮盘间法向接触刚度kf由式(1)得到，切向刚度kq根据式(2)［10］得到。

图2 微观尺度的有限元计算模型Fig.2 Micro-scale finite element model

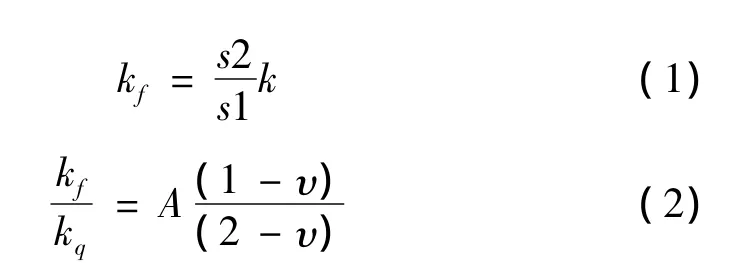
式中:A=2，υ=0.3 为泊松比，取kq=0.82kf。

1.2 附加弹簧单元建立

轮盘间接触界面处理成无质量、法向刚度为kf、切向刚度为kq的附加弹簧单元，其在系统中的附加刚度矩阵可根据弹性势能定律推导得到。附加弹簧单元势能大小由接触界面两侧附属节点的动态坐标确定。对于接触端面中心点来说，其坐标由固结连接于盘轴中心节点的动态坐标(x，y，ψ，φ)确定(轮盘与其邻近轴段简称盘轴单元)，因而其上距盘轴中心r的一点的坐标可如下确定为:建立系统的绝对坐标系oxyz，在此坐标系中t时刻盘轴1中心的坐标为(x1，y1，z1)，角坐标为(ψ1，φ1，ωt)。然后通过移轴将坐标系原点移至所考虑盘轴的中心，得到盘轴坐标系o'x'y'z'，如图3所示，再将圆盘绕y'轴旋转φ1角到达o1x1y1z1，再绕x1轴反向旋转ψ1角到达o2x2y2z2，最后再绕z2轴以角速度ω正向旋转ωt角，最终到达圆盘的随动坐标系o3x3y3z3。

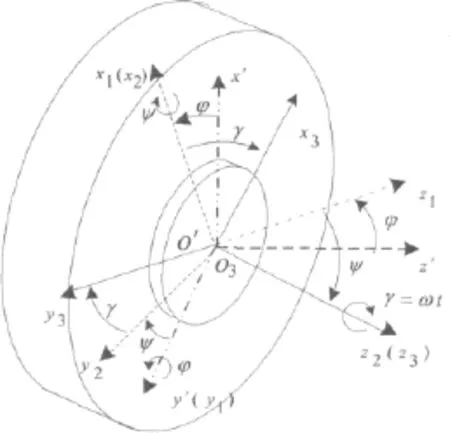
图3 刚性盘轴段坐标变换示意图Fig.3 Coordinate transformation of rigid plate

因此，在盘轴的随动坐标系o3x3y3z3中，接触界面的固接点A(xA，yA，zA)的坐标可表示为式(3)，其中x1，y1，z1分别是盘1 的动态位移，ψ1，φ1则为盘1 的动态转角，(为附加弹簧单元的端点在圆盘上的位置转角。接触界面另一端对应的固结点B(xB，yB，zB)的坐标可类似表出。

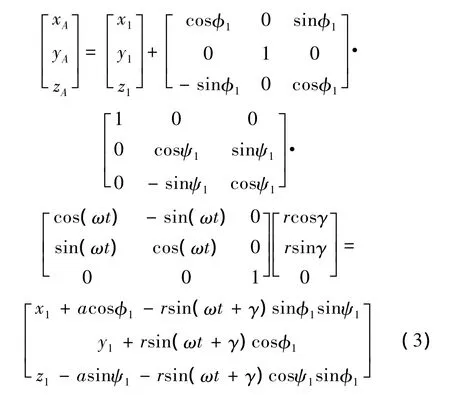
式中:a=rcos(ωt+γ)。

根据线性弹簧变形的势能原理，接触界面的弹性势能表示为:

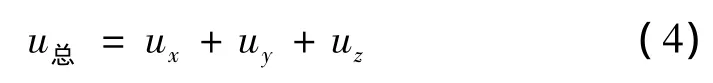
在径向x方向上的势能Ux，可根据弹簧此方向上变化量产生的势能对接触界面积分得出:

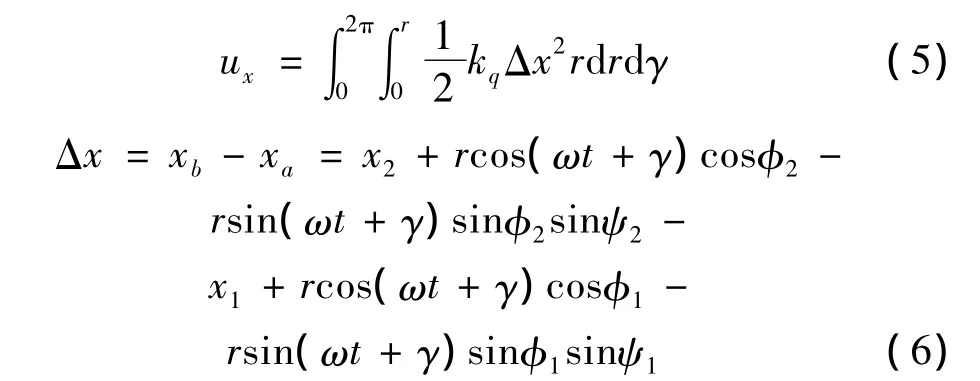
Δx2取一阶近似后可得:

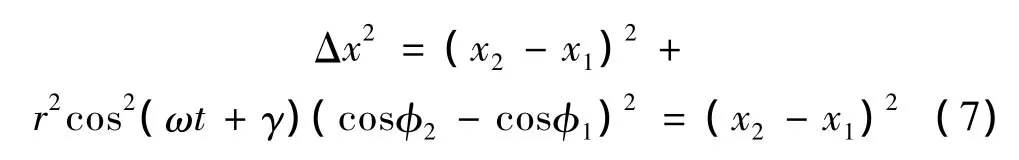
式(7)代入式(5)可知:

在径向y方向上的势能Uy，其弹簧势能与x方向推导类似，有:

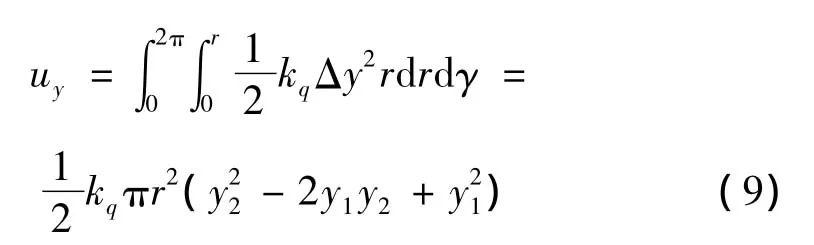
在轴向z方向上，有:

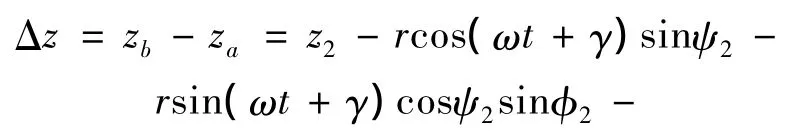
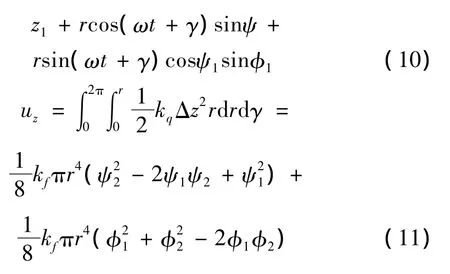
可知:

其中:

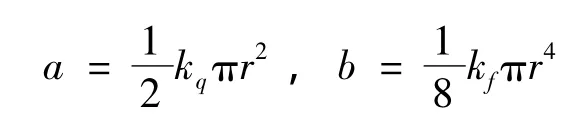
可推出接触界面处理为附加弹簧单元后，其附加刚度矩阵ke为:

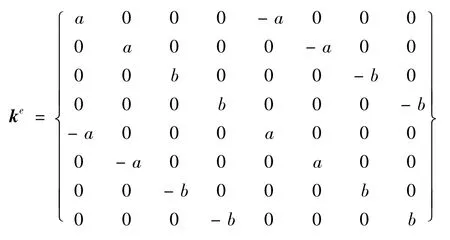
2 系统方程

对于预紧后的组合转子整体转轴，直接采用了计及轴向力的铁木辛格梁轴单元进行离散［11］，如图4所示。在整体转轴的动力方程中，根据哈密顿原理加入轮盘间接触界面、刚性圆盘和周向均布拉杆［12］的影响后，最终给出预紧后的拉杆组合转子轴承系统动力学方程:

式中:MS=Mr+Md，GS=Gr+Gd，

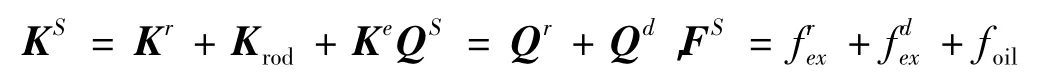
其中:Ms，Gs，Ks∈Rm×m分别是系统的质量、阻尼和刚度矩阵;Qs，Fs∈Rm×m分别是系统的重力和外力矢量;Ke为附加弹簧单元提供的附加刚度矩阵;Mr，Gr，Qr∈Rm×m分别为转轴的质量、阻尼、刚度矩阵;Md，Gd，Qd，fexd分别为刚性圆盘的质量、陀螺矩阵及重力和不平衡力矢量;foil为轴承力;系统的位移矢量为:xS={x1y1ψ1φ1…xmymψmφm}T。

其中:xj，yj和ψj，φj(j=1，2，…，p)分别为第j个节点的横向位移及转动自由度。

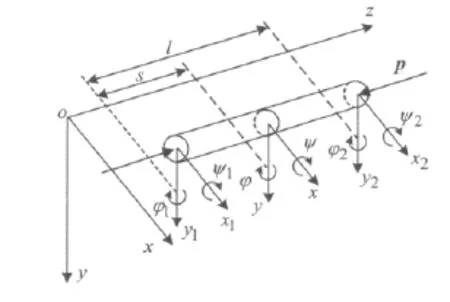
图4 预紧后的铁木辛格梁轴有限单元模型Fig.4 Timoshenko beam-shaft element after tightening

3 分析方法

假设作用于系统的载荷为周期为T的周期载荷:

则系统的稳态解为周期解、伪周期解及混沌解。对于轴承转子系统而言，工频周期解是其本征解，随外参数转速ω、不平衡量e等的变化，此解将发生失稳，而产生新的稳态解形式，如伪周期解及混沌解，或发生绝对失稳，因此求取系统的周期解及其稳定性分叉规律便成为研究此类系统非线性特性的主要内容。

3.1 周期解求解

应用打靶法求解式(13)动力系统周期解的问题可转化为两点边值问题:

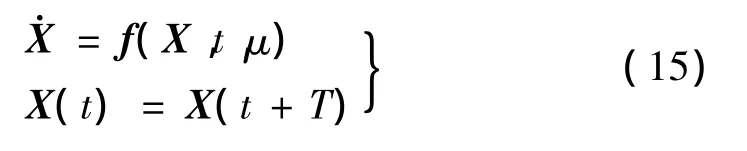
其中:

式中:μ为系统参数，如系统转速ω、不平衡量e等等。将式(15)积分一个周期T，则如下式得到满足时可求得一个T周期的周期解Xs。

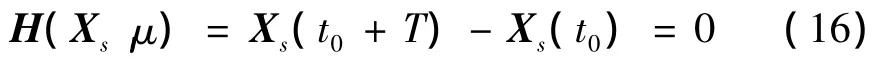
对于一个给定的参数μ=μs，对应的周期解Xs可通过对式(17)应用牛顿迭代法求得。其雅克比矩阵为:

矩阵J可通过将下式与式(15)一起对于系统轨迹Xs(t0+t)积分一个周期求出:)

显然当以［Xs(t0)，I］作为初始值积分一个Poincare 映射周期T，δS(t0)=I时，δS(t0+t)=J。以上即为打靶法的基本思路。在此基础上，采用周期解延续追踪算法［13］当外参数变化时对周期解进行预估校正，有效地得到外参数变化时周期解的演化规律。当已经求得外参数μ=μn时的周期解Xn，则第n+1步解的迭代初值为:

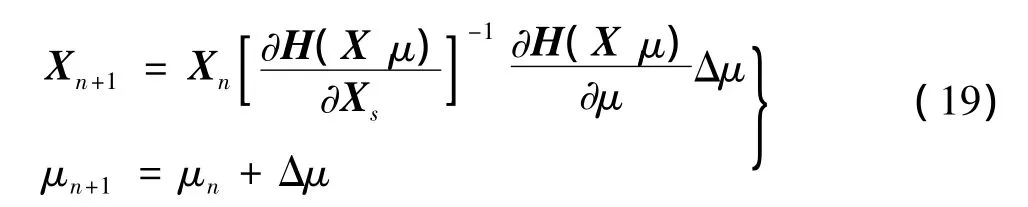
而后在μ=μn+1处用打靶法进行校准即可。∂H(X，μ)/∂μ可以通过将式(20)对轨迹Xs(t0+t)积分求得:

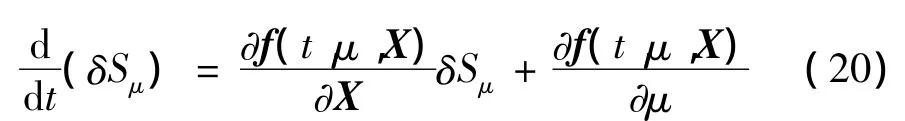
当δSμ(t0)=0 时，δSμ(t0+T)=∂H(X，μ)/∂μ。

3.2 稳定性判别的FLOQUET理论

本文周期解判稳采用Floquet理论［14］，通过求解周期解的状态转移矩阵即雅克比矩阵J的特征值(Floquet乘子)来进行。当所有Floquet乘子均位于复平面的单位圆内时，周期解稳定，而其随外参数变化穿越单位圆的不同，周期解会发生不同的分叉形式:

(1)当一个模最大的Floquet乘子由(1，0)穿出单位圆时，周期解失稳分叉的可能方式主要有鞍结分叉、叉型分叉和对称破损分叉等多种情况;

(2)当一个模最大的Floquet乘子由(-1，0)穿出单位圆时，周期解将通过倍周期分叉而失稳;

(3)当一对模最大的Floquet乘子以共轭复数方式(虚部不为0)穿出单位圆时，周期解经Hopf型伪周期分叉产生伪周期解。

4 计算实例及结果对比

如图5所示的一个典型拉杆组合转子轴承系统，其转子可以看作是由一根整体转轴和固结于其上的4个刚性轮盘，4个轮盘通过3个接触界面连接，并由固结预紧的12根周向均布拉杆组成，此处预紧量大小参照工程中重型燃机选取的拉杆长度的千分之一。计入接触界面以前，系统视作为一根整体转子，无界面单元存在，此时系统离散为11段12个节点;计入接触界面以后，轮盘间界面处理为附加弹簧单元，此时系统离散为17段18个节点。模型材料为密度ρ=7 800 kg/m3，弹性模量E=2.1×1 011的钢;接触界面粗糙度0.4 μm(kf=1.72e12，kq=1.41e12)，界面摩擦系数 0.15，轴径dshaft=0.08 m、长度lshaft=1.1 m;界面效应计入前后模型均采用文献［12］中建立的Pinkus无限长轴承模型，它是比较简单的轴承力形式之一。

图5 拉杆组合转子轴承系统结构及单元划分示意图Fig.5 Structure and finite element of FRRBS

对于此系统，首先采用前述介绍的方法，建立此系统的动力学模型，轮盘间接触界面的附加刚度矩阵通过相应的附加弹簧单元添加到系统中;转子不平衡量的添加方式为在4个刚性轮盘上加同相位的无量纲质量偏心距e;径向轴承力添加到对应轴承节点上，其主要研究内容和结果整理如下:

4.1 计入接触界面对系统e-ω特性的影响:

图6为界面计入前后系统e-ω转迁图中各类符号均为计及界面影响后的标记，无界面时见文献［12］。

通过计算，得到了计入接触界面前后此拉杆组合转子轴承系统稳态解随参数ω和e的分布变化规律，如图6。

可以看出，计及接触界面后系统稳态解的稳定性分叉规律与整体转子相比较，同样具有以下特征:

同步周期解的Hopf型伪周期分叉集Ⅱ与倍周期分叉集Ⅰ及e=ecr将所研究的参数域划分为如图6的同步周期解①、伪周期解②及倍周期解③;同步周期解的分叉在e较小时表现为伪周期分叉，而在e较大时发生倍周期分叉;不平衡量e较小时伪周期失稳转速随e增大而略微增大，较大时倍周期失稳转速随e增大而减小;系统响应峰处倍周期分叉集呈鞍形变化。

然而接触界面的计入，为系统带来的影响也是显著的:

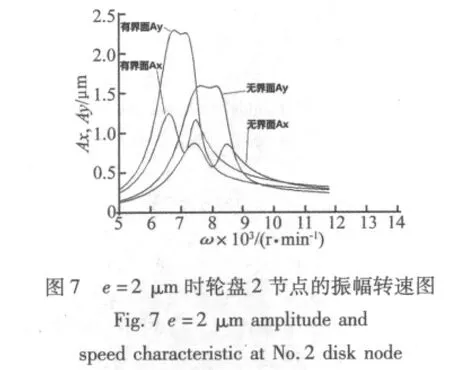
(1)轮盘间接触界面使得整体转子的刚度降低，导致其第一临界转速明显下降，如图7所示波峰所在位置明显左移，系统稳定工作的e-ω参数区域整体左移。故在工程实际中此类组合转子尽量提高轮盘间接触界面加工质量，以保证足够的接触刚度，可以有效降低接触界面对临界转速的影响。

(2)接触界面使倍周期分叉集Ⅱ和伪周期分叉集Ⅰ的临界不平量ecr增大，说明在第一临界转速以上工作的转子，较大的不平衡量将使得系统更容易发生Hopf型伪周期分叉而失稳。同时，当系统工作在第一临界转速后鞍形区域内时，定转速下发生倍周期分叉的临界不平衡量有所增大。此处界面影响一定程度上提高了系统在该e-ω参数区域稳定运行的能力。

(3)在不同参数区域，界面的作用力大小不一样，其对系统稳定性的影响不同。对高转速区域失稳转速的影响相对较大，低转速区域失稳转速的影响相对较小。

(4)由于接触界面导致整体转子刚度的降低，转子的振动量较之整体转子时有所增大。如图7，其最大振动量在y和x方向上均有显著增大，对转子的振动特性影响明显。

4.2 定参数下带界面转子系统典型轨迹

此处采用图 6 中标记的 A(11 200 r/min，2 μm)，B(6 500 r/min，6 μm)，C(10000 r/min，11 μm)和D(12 450 r/min，11 μm)四个典型点的转速和不平衡量参数，对比了界面计入前后系统的典型轨迹。结果如图8所示，其中图 8(a)代表整体转轴的转子轴承系统，图8(b)代表计及接触界面的转子轴承系统。

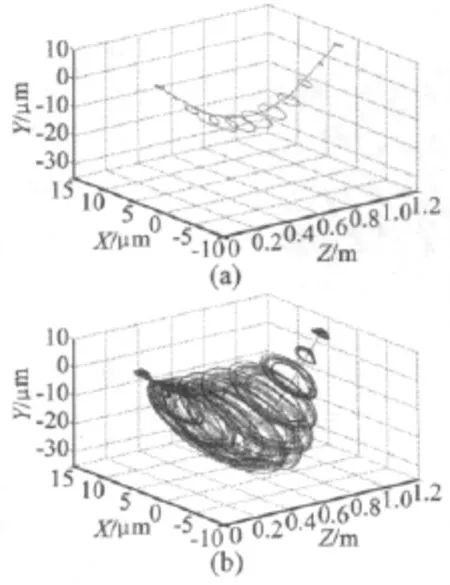
图8 ω =11 200 r/min，e=2 μmFig.8ω =11 200 r/min，e=2 μm

图9 ω =6 500 r/min，e=6 μmFig.9ω =6 500 r/min，e=6 μm

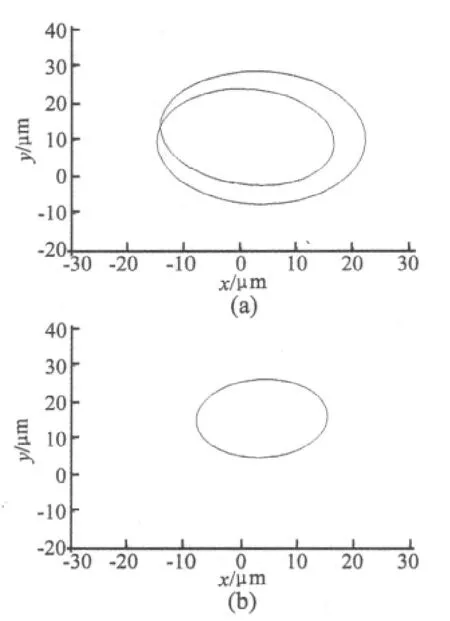
图10 ω =1 000 r/min，e=11 μmFig.10ω =1 000 r/min，e=11 μm

图11 ω =12 450 r/min，e=11 μmFig.11ω =12 450 r/min，e=11 μm

图8表明在高转速区域小不平衡量时，整体转轴系统的稳态周期解在接触界面影响下变为伪周期解，且振动量明显增大;图9表明低转速区域接触界面使得整体转轴系统由同步周期解变为倍周期解，且振动加剧;图10表明在C点参数区域接触界面使得倍周期运行状况的系统进入到稳态同步周期解，一定程度上改善了系统稳定性;图11表明在D点参数区域发生倍周期分叉的整体转轴系统，在计入接触界面以后更容易发生伪周期分叉而导致失稳。

5 结论

本文针对拉杆组合柔性转子轴承系统，完成了计及轮盘间接触界面影响的动力学系统建模，并对接触界面对其非线性动力学特性的影响进行了研究，所得出主要结论如下:

(1)接触界面使得整体转子刚度降低，导致第一临界转速减小，并且使得系统振动加剧，最大振动幅值明显增大;

(2)系统稳定工作的同步周期解e-ω区域受接触界面的影响整体左移，且在高转速区域的影响量较之低转速区域大;

(3)在高转速区较大不平衡量时，转子系统的分叉形式可能受界面影响，由倍周期分叉失稳变为位周期分叉失稳。

［1］Lund J W，Nelson H B.Instability threshold of an unbalanced rigid rotor in short journal bearings［C］//IMechE，Proceeding IMechE Conference on Vibration in Rotating Machinery，1980，Cambridge，UK.IMechE，1980:91-95.

［2］ Kim Y B，Noahst S T.Bifurcation analysis for a modified jeffcott rotor with bearing clearance［J］.Nonlinear Dynamics，1990，1(3):221-241.

［3］Sundararajan P，Noah S T.Dynamics of forced nonlinear systems using shooting/arclength continuation methodapplication to rotor system［J］.ASME Journal of Vibration and Acoustics，1997，119(1):10-20.

［4］ Zheng T，Hasebe N.Nonlinear dynamic behaviors of a complex rotor-bearing system［J］.ASME Journal of Applied Mechanics，2000，67(3):485-495.

［5］汪光明，饶柱石，夏松波.拉杆转子力学模型的研究［J］.航空学报，1993，14(8):419-423.

WANG Guang-ming， RAO Zhu-shi， XIA Song-bo. The analysis of mechanical model of rod fastening rotor［J］.Acta Aeronautica et Astronautica Sinica，1993，14(8):419-423.

［6］饶柱石.拉杆组合式特种转子力学特性及其接触刚度的研究［D］.哈尔滨:哈尔滨工业大学，1992.

［7］王艾伦，骆 舟.拉杆转子轴向振动的动力学模型［J］.机械工程学报，2009，20(13):1524-1527.

WANG Ai-lun，LUO Zhou.Research on rod fastening rotor dynamicsaxialvibration［J］. JournalofMechanical Engineering，2009，20(13):1524-1527.

［8］何 鹏，刘占生，张广辉，等.分布式拉杆转子动力学建模与分析［J］.汽轮机技术，2010，52(1):4-9.

HE Peng， LIU Zhan-sheng， ZHANG Guang-hui， et al.Dynamic modeling and analysis of distributed rod fastening rotor［J］.Turbine Technology，2010，52(1):4-9.

［9］李辉光，刘 恒，虞 烈.粗糙机械结合面的接触刚度研究［J］.西安交通大学学报，2011，45(6):1-6.

LI Hui-guang，LIU Heng，YU Lie.Study on contact stiffness of rough mechanical joint surface［J］.Journal of xi'an Jiaotong University，2011，45(6):1-6.

［10］Valadez G M，Baltazar A，Joyce D R S.Study of interfacial stiffness ratio of a rough in contact using a spring model［J］.Wear，2010，268(3-4):373-379.

［11］ Nelson H D.A finite rotating shaft element using timoshenko beam theory［J］.ASME J.Mech.Des.，1980，102:793-803.

［12］刘 恒，陈 丽.轴向均布拉杆柔性组合转子轴承系统的非线性动力特性［J］.机械工程学报，2010，46(19):53-62.

LIU Heng， CHEN Li. Nonlinear dynamic analysis of a flexible rod fastening rotor bearing system［J］.Journal of Mechanical Engineering，2010，46(19):52-62.

［13］Fey R H B，Van Campen D H，De Kraker A.Long term structuraldynamics ofmechanical systems with local nonlineariyies［J］.ASME Journal of Vibration and Acoustics，1996，118(4):147-153.

［14］Ho Y S，Liu H，Yu L.Effect of thrust magnetic bearing on stability and bifurcation of a flexible rotor active magnetic bearing system［J］. ASME JournalofVibration and Acoustics，2003，125(3):307-316.