60 MN内高压成形机拉杆预紧力对机身刚度影响
朱成成,谢文才,张 琦,刘 强,赵升吨
(1.西安交通大学机械学院,陕西 西安 710049;2.一汽轿车股份有限公司技术部,吉林 长春 130012)
0 前言
内高压成形技术 (IHF)是一种用于加工复杂空心零件的冷成形工艺,加工范围比较广,可以加工各种各样的复杂空心零件。内高压成形机是实现这种工艺的设备,用于制造管道、压力容器等类型的工件。大型内高压成形机是衡量国家机械制造水平的重要装备[1-2]。该设备通常为拉杆预紧的组合框架式结构。拉杆预紧力的大小,对机身的刚度、稳定性、安全性和加工精度都有影响。预紧力不足,则机身的刚度无法保证;预紧力过高,将致使拉杆过度变形而产生早期断裂[3]。国内大型内高压成形机的设计对拉杆预紧力,只能通过一些经验公式确定预紧力的大小,60 MN内高压成形机高12 m,左右方向宽约6 m,前后方向约宽2.5 m。本文使用有限元软件ABAQUS对60MN内高压成形机在各种预紧力情况下的状态仿真,进行相关分析。对该高压成形机拉杆预紧力与机身刚度、机身应力的关系进行了研究,确定了该机拉杆预紧力的合理取值范围为1~1.5倍工作载荷,并验证了设计的合理性。通过分析,提出了针对该机拉杆直径的优化设计方案:因靠近载荷的拉杆受力比较大,且该力的大小与预紧力大小有关,所以这些拉杆需要对强度与刚度重点设计,增大直径是简单有效的方式。
1 有限元模型建立
1.1 建立几何模型
根据设计图纸,使用三维软件建立模型。为便于有限元计算,将整体分为上横梁、下横梁、滑块、工作台、液压缸、立柱等六个部分,拉杆分为两组单独是一个部分,两组拉杆的几何模型完全相同:第一组拉杆 (拉杆1)处于机身内侧,第二组拉杆 (拉杆2)处于机身外侧。将模型导入ABAQUS。建立好的模型如图1所示。

图1 60 MN内高压成形机模型Fig.1 Model of 60MN internal high-pressure forming machine
1.2 材料定义
60MN内高压成形机机身的材料为Q235碳素钢,而拉杆的材料为45钢。

表1 材料性能Tab.1 Material performances
1.3 网格划分
用四面体单元C3D4为立柱划分网格,使用六面体单元C3D8R为其余部分划分网格。为更好的对实际工况进行模拟,在ABAQUS中建立了一个长方体作为对工作条件下的模具的代替,材料为Q235。模型划分网格之后如图2所示。

图2 机身网格划分Fig.2 Meshing of machine body
1.4 约束及载荷的施加


2 分析
2.1 机身刚度定义
刚度的大小影响机身的稳定性、加工精度等,是一项重要的指标。刚度定义为物体在外加载荷作用下,抵抗变形的能力。因为该机的工作载荷最终通过模具将力传给机身,主要的影响就是引起机身竖直方向的变形,所以本文只考虑机身整体的竖直刚度[4]。
竖直刚度是指在工作载荷作用下,机身在竖直方向产生单位变形所需的压力。以机身上横梁的下底面中部与下横梁上底面中部的平均距离作为机身位移变化的测量对象 (无明确说明时,位移变化量即指机身竖直方向的位移变化量)。
竖置刚度及位移变化量公式为[5]

式中,k为机身竖直刚度,N/m;F为工作载荷,N;Δh为机身位移变化量,即加载后,上横梁与下横梁之间高度的变化 (m)。

式中,h1为加载后,上横梁与下横梁之间的高度,m;h0为加载前,上横梁与下横梁之间的高度,m。
该机的高度比较大,而加载过程中的位移变化量又比较小,所以如果直接以竖直刚度作为衡量指标,则其巨大的数值及增量,难以看出变化规律,所以本文用位移变化量的大小衡量机身刚度。
2.2 预紧力与机身刚度关系
2.2.1 等值施加预紧力
取所有拉杆预紧力倍数都相同,依次为0、0.5、1、1.5、2、2.5。
经有限元计算,当拉杆预紧力倍数为1.5时,机身的应力及应变云图如图3所示。可以看出,机身的应力比较小,立柱、横梁的变形量也相当小,而应力及变形最大的地方出现在拉杆部分。


图3 等值施加预紧力时机身的应力应变云图Fig.3 Stress nephogram of internal high-pressure forming machine
拉杆预紧力倍数与机身位移变化量的关系如图4所示。

图4 位移变化量曲线Fig.4 Deformation nephogram of internal high-pressure forming machine
由此可见,机身在拉杆预紧力等值加载时,竖直刚度随着预紧力的增加而变大。但是随着拉杆预紧力倍数的增大,机身位移变化量降低的速度在减小。当拉杆预紧力倍数达到1.5或以上时,位移变化量已经足够小,不适合使用增加预紧力的方法继续提高机身刚度。
根据图像的特性,可以对该曲线进行数值拟合,设该曲线的近似方程为
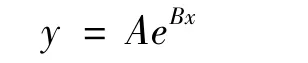
式中,x为预紧力倍数;y为位移变化量;A与B为需要确定的系数。
将计算所得的五组数据,每两组作为一对,将原方程取自然对数之后,带入该方程求解A与B。最后将所有求出的结果取算术平均值,得y=11.7315e-1.601x。拟合曲线与原始曲线的比较如图5所示。可以看出预紧力倍数为1~2.5时,拟合曲线和原始曲线很接近,此时可用拟合曲线进行刚度的近似求解。

图5 曲线比较Fig.5 Curve of displacement variable quantity
2.2.2 施加非等值预紧力
为找出刚度最高时各拉杆的预紧力关系,对两组拉杆施加不同大小的预紧力,测定这种条件下机身的刚度。同组的拉杆预紧力相等,每组拉杆预紧力倍数依次选用0、0.5、1、1.5、2、2.5。
当第1组拉杆预紧力倍数为0.5,第2组预紧力倍数为1.5时,该机的应力及变形云图如图6。以第1组拉杆预紧力的倍数为x坐标,第2组拉杆预紧力的倍数为y坐标,机身的竖直位移变化量为z坐标,通过matalab插值计算,可以得到位移变化量与两组拉杆预紧力倍数的关系,如图7所示。


在非等值预紧力的作用下,机身刚度变化有如下特点:
(1)由图3和图6比较可知当两组拉杆施加不同的预紧力时,机身的应力分布以及变形状况都会发生改变。预紧力对机身的应力及变形状态具有显著影响。
(2)由图7可知,机身位移变化量曲面呈抛物面状,随着预紧力的增加,该面越来越接近平面,并且斜率非常小。无论哪一组预紧力的增加,都会引发机身刚度的增强。在一定范围内,通过为两组拉杆施加不同大小的预紧力以增加机身刚度的方法,对于该机并不可行。两组拉杆都施以可取范围内最大的预紧力时,机身将会获得最大的刚度。当拉杆预紧力倍数都达到1.5以上时,拉杆预紧力的增加已经不能显著改变机身的竖直刚度。
2.3 机身应力与预紧力的关系
拉杆预紧力等值加载,取拉杆预紧力倍数为0、0.5、1、1.5、2、2.5,得到拉杆预紧力倍数与机身在施加工作载荷之前及加载之后最大应力的关系,如图8所示。
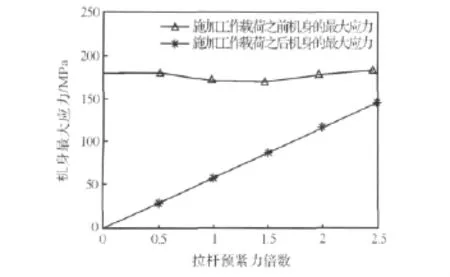
图8 拉杆预紧力倍数与机身最大应力关系图Fig.8 Deformation nephogram of internal high-pressure forming machine
加载之前,机身最大应力随拉杆预紧力倍数的增加以线性规律递增。加载之后,机身的最大应力随拉杆预紧力倍数的增加呈现先降后升的规律,当预紧力倍数在1~1.5之间时,机身的最大应力比较低。拉杆预紧力太小,不能影响机身最终的状态,立柱与横梁的接合面还是会被拉开,各处应力状态也区别不大;当拉杆预紧力逐步增大时,立柱与横梁的结合面会有越来越大的相互作用力,使得整个机身都受到了拉杆的影响,平均应力增加,而应力分布的改变则使得应力集中程度有所不同,所以最大应力有波动。
机身材料Q235的屈服强度为235 MPa,而机身的最大应力约为180 MPa,所以拉杆预紧力倍数为2.5或者更低时,机身的强度应该足够。考虑到拉杆预紧力倍数为1~1.5时,机身的最大应力值较低,拉杆预紧力倍数在这一区间比较合适。
2.4 拉杆应力与预紧力的关系
拉杆平均应力通过导出所有单元的Mises应力值,求其平均得到。

对所有拉杆施加等值预紧力时,以拉杆全体作为研究对象,则拉杆的最大应力、平均应力与拉杆预紧力倍数的关系如图9所示:

图9 拉杆应力与预紧力倍数关系图Fig.9 Curved surface of displacement variable quantity when non-equivalence preload of pull bar
随着预紧力的增加,拉杆的平均应力和最大应力在不断变大,并且增幅相近。根据仿真结果,当拉杆预紧力倍数为1.5时,拉杆的最大应力为345 MPa、平均应力296 MPa,接近45钢的屈服极限。所以拉杆预紧力倍数不能超过1.5。在计算过程中,发现两组拉杆的应力状态并不相同。两组拉杆的应力与拉杆预紧力倍数的关系见图10所示。


图10 两组拉杆的应力与拉杆预紧力倍数关系Fig.10 multiple of pull bar preload force versus maximum stress of machine body
由图10a可知,施加工作载荷之后,第1组拉杆的最大应力和平均应力始终大于第2组拉杆的应力,并且同名应力的变化趋势相同。由图10b可知,两组拉杆的最大应力差值约为18 MPa,随着拉杆预紧力倍数的增加,该值先减小后缓慢变大。当拉杆预紧力倍数为1时,两组拉杆的最大应力之差最小,为17.1 MPa。两组拉杆的平均应力差值也呈现先减小后变大的趋势,但是最小值出现在预紧力倍数为2的时候。因为第1组拉杆受到的应力比较大,所以需要将第1组拉杆的应力降低或者将拉杆的强度增加,否则很可能先于第2组拉杆发生损坏。
可以看出,该型机床靠近工作载荷的拉杆在工作过程中受力比较大,在设计时可以考虑增加其直径,使各拉杆的应力值相同且都比较小。
如需为拉杆增加安全系数,可在图10a中对第1组拉杆的最大应力取点,确定相应的预紧力倍数。
通过以上分析发现,拉杆预紧力的大小并不能显著改变机身的应力值,仅能改变应力分布。但是预紧力对拉杆的应力大小和分布都有很大的影响,特别是使得两组拉杆的应力状态不同。这是因为工作载荷与拉杆的拉力会使得机身发生弯曲,导致拉杆的弯曲变化,改变了拉杆的应力状态。
3 结论
(1)对于60 MN内高压成形机,各组拉杆施加不同预紧力并不能显著降低机身的位移变化量,两组拉杆同时施以可取范围内最大的预紧力,机身将会获得最大的刚度。等值加载,拉杆预紧力倍数小于2时,机身位移变化量随着预紧力倍数的增加而显著减小;当预紧力倍数超过2时,机身位移变化量只能随着预紧力倍数的增加略有减小,此时位移变化量已经非常小。所以只考虑刚度时,选取各拉杆预紧力倍数相等,在1~2之间,且取值越大,刚度越好。
(2)考虑机身和拉杆应力因素时,拉杆预紧力倍数应在1~1.5之间,此时机身的最大应力较小,拉杆应力也在允许范围内。过高的预紧力会使得拉杆的应力过大。
(3)综合考虑刚度及强度因素,该机的拉杆应该采用等值预紧的方式,预紧力倍数在1~1.5之间,且取值越大,刚度越好,应力值越大。
(4)靠近载荷的拉杆可以将直径增大,使得各拉杆的应力状态接近且应力值较小。
[1]Hans-Jörg Bullinger,Technology Guide:Principles,Applications,Trends[M].Springer,2009.
[2]Heinz Tschätsch ,Metal Forming Practise:Processes,Machines,Tools[M].Springer,2006.
[3]段志东,苏铁明.组合机架的刚度分析和拉杆预紧力研究 [J].机械科学与技术,2009(4):450-454.
[4]Steve Krar,Arthur Gill,Exploring Advanced Manufacturing Technologies[M]. Industrial Press,Inc,2003.
[5]周杰,伍驭美.拉紧螺栓预紧力对闭式组合机身内高压成形机精度的影响[J].锻压机械,2001,36(1):35-37.
[6]蔡怀崇,闵行.材料力学基础 [M].西安:西安交通大学出版社,2004.

