旋转机械故障诊断的图形识别方法研究

窦 唯，刘占生

(1.北京航天动力研究所，北京 100076;2.哈尔滨工业大学 能源科学与工程学院，哈尔滨 150001)

目前，应用于旋转机械故障诊断的智能方法，如神经网络、模糊推理、专家系统等诊断方法的故障特征多数是来自于对振动数据进行各种信号处理提取得到的，然后进行诊断识别［1-4］。但是在实际工程应用中更为关注的是一些由振动数据得到的参数图形，如振动三维谱图、轴心轨迹图及趋势图等，因为这些图形中含有设备运行过程中的大量状态信息，在以往的故障诊断系统中图形中的信息没有得有效的利用，在一定程度上影响诊断技术的推广和利用。

近年来，利用图形识别技术进行故障诊断已引起人们的极大兴趣，如利用振动三维谱图诊断发电设备中的各种常见故障［5-6］;提出了在二维全息谱的基础上重构低频和倍频轴心轨迹的方法诊断旋转机械常见故障［7］;文献［8］探讨了图形处理技术在柴油机振动故障诊断中的应用，为图形识别技术能应用在旋转机械故障诊断中提供了新的思路;文献［9-11］根据图形识别技术研究了基于灰度-基元共生矩阵、灰度-梯度共生矩阵及融合灰度共生矩阵的旋转机械故障诊断方法。

图形信息在以往的旋转机械故障诊断中没有得到较好的利用，主要是图形特征的提取和描述困难。因此，能否准确描述图形的纹理特征也是制约着图形识别技术在故障诊断中应用的瓶颈之一。

灰度图形特征主要包括形状、纹理等。纹理信息是图形的最基本特征，包含着图形主要目标边界信息，反映了图形本身的属性。纹理分析方法有统计法、结构法等［12］。本文根据统计方法和结构方法的各自特点，针对旋转机械振动参数图形提出了基于灰度-基元-梯度共生矩阵的旋转机械故障诊断方法，该方法首先根据旋转机械图形的特点，将振动三维图形转化为二维灰度图形，然后根据灰度图形的纹理分布特点，利用图形的灰度空间分布情况(概率)、梯度空间分布规律以及各像素点与其领域像素点之间的空间关系和描述纹理的纹理基元将统计法和结构法结合起来描述图形的纹理特征，这样可以有效地提取和挖掘旋转机械状态参数图形中纹理特征信息，然后利用人工神经网络实现旋转机械故障诊断。在600MW模化汽轮机转子试验台上进行了转子正常、转子不平衡、转子不对中、轴承松动、汽流激振和动静碰磨6种状态试验，诊断结果表明所提出方法具有较高的诊断准确率，为旋转机械故障诊断探索了一条新路。

1 基于灰度-基元-梯度共生矩阵的旋转机械状态参数图形特征提取

图形特征主要体现在灰度信息、形状信息和纹理信息等方面。灰度共生矩阵是图形纹理特征的统计描述方法，而基元方法是图形纹理特征的结构描述方式。根据灰度图形的纹理分布特点，利用图形的灰度空间分布情况(概率)、描述纹理的纹理基元及能清晰地描绘图形内各像素点灰度与梯度的分布规律及像素点与其邻域像素点的空间关系的灰度-梯度空间，将统计法和结构法结合起来描述图形的纹理特征。这样即能利用梯度的方向性反映纹理的方向性，又能充分利用统计方法和结构方法的各自优点较好地描绘图形的纹理特征，从而可以有效地提取和挖掘旋转机械状态参数图形中灰度统计和空间结构的纹理特征信息。因此，针对旋转机械灰度纹理图形的特点，在本文中提出以描述图形纹理特征的灰度-基元-梯度共生矩阵的统计量作为特征向量进行旋转机械振动故障诊断方法研究。

1.1 灰度-基元-梯度共生矩阵

灰度-基元-梯度共生矩阵是利用图形的灰度信息、反映图形纹理结构的基元信息，以及反映图形灰度空间变化率的梯度信息，将它们综合起来形成一种数学描述方法，用以提取图形纹理的数字特征。

定义:设B(m，n，p)为灰度-基元-梯度三维共生矩阵，F(i，j)为图形灰度矩阵，TG(i，j)为归一化的图形基元矩阵，QG(i，j)为归一化的图形梯度矩阵。统计使F(i，j)=m，TG(i，j)=n，QG(i，j)=p的像元数量，该值即为灰度-基元-梯度三维共生矩阵的第(m，n，p)个元素值，即:

其中:m，n，p=1，2…16，所以B(m，n，p)矩阵中有 163个元素。

计算灰度-基元-梯度共生矩阵，首先按照灰度矩阵求出基元矩阵和梯度矩阵，由于图形的灰度矩阵、基元阵和梯度矩阵的值域存在差异，需要将它们统一起来，进行正规化处理。把这些值域不同的矩阵有效地等价到具有共同值域的矩阵上来，这样就可以得到了灰度-基元-梯度三维共生矩阵B。

1.2 灰度-基元-梯度共生矩阵的图形特征提取

三维共生矩阵尽管能反映图形的特征，但是冗余信息过多，为了准确地对旋转机械进行故障诊断，需要根据旋转机械参数图形特点从三维共生矩阵提取统计数字特征，本文中从三维共生矩阵中提取角度二阶矩、对比度、绝对值、反差矩、自相关系数、熵6个统计特征。

角度二阶矩:

对比度:

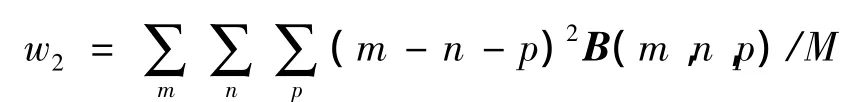
绝对值:

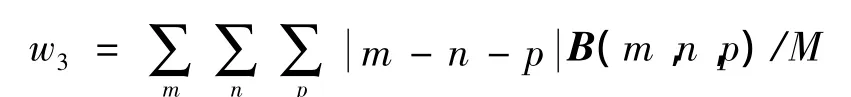
反差矩:

自相关系数:

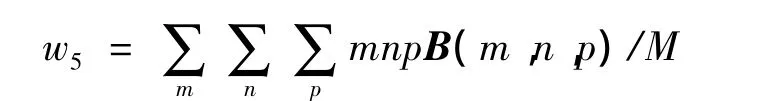
熵:

M为三维共生矩阵元素总数，如果灰度、基元和梯度归一化为16级别，则三维共生矩阵元素总数M为163。

这样由以上6个特征就可以组成了图形的纹理特征向量:

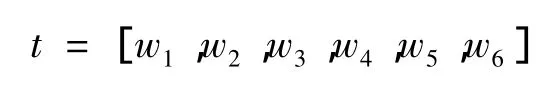
由于该特征向量中的6个分量的物理意义和取值范围不同，小的分量和大的分量相比，在以欧氏距离作为量度时，小的分量容易被忽略，所以需要对各个特征分量进行内部特征归一化。本文用高斯归一化方法后，在计算相似距离时，可使各分量具有相同的权重［9］。

原始特征向量为［w1，w2…w6］，归一化的特征向量为［T1，T2…T6］，归一化步骤为:① 计算各个原始特征向量的平均值m和标准差σ。② 进行归一化运算:

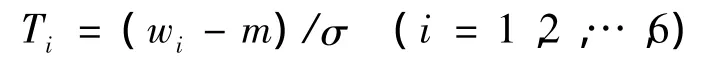
2 基于人工神经网络的故障诊断

根据上文所提供的纹理特征，运用人工神经网络进行旋转机械故障识别。BP神经网络的应用研究较多，但是BP神经网络的由于收敛速度慢，限制了它在故障诊断领域中的应用。BP神经网络是全局逼近网络，对于每个输入输出数据对，网络的每一个权值均需要调整，从而导致学习速度很慢，这个缺点对于在线诊断常常是不可忽视的。RBF网络是一种局部逼近神经网络，对于每个输入输出数据对，只有少量的权值需要进行调整，因而具有学习速度快的优点。RBF网络在逼近能力、分类能力和学习速度等方面均优于BP网络。RBF网络结构如图1。该网络为2层网络，其中隐层的转换函数为径向基函数，输出层的转换函数为线性函数。图中R为输入特征向量的维数(R=6);Y1为隐层神经元数(Y1=3);Y2为输出层神经元数(Y2=6)。

图1 RBF神经网络模型Fig.1 RBF neural network

利用上文提取的样本特征向量对所建立的神经网络进行学习训练后即可诊断识别，对于实际的故障诊断问题，经数据采集的原始振动信号为时间序列信号，一般需要对原始训练样本进行预处理生成三维谱图，根据旋转机械振动特点，将三维图形转换为二维灰度图形，对灰度矩阵进行处理，提取基元阵、梯度阵及灰度-基元-梯度三维共生矩阵及其统计量特征，对纹理特征向量并进行归一化处理，这样就得到故障特征向量样本。在有了含大量故障信息的故障样本后，就可以训练所建的神经网络，训练后的网络即可实施诊断。在线进行故障诊断过程时，必须按照同样的方法对信号进行处理和特征提取。训练及诊断过程如图2所示。在图2中，上半部流程为离线学习过程，下半部为诊断过程。在实际诊断过程中，只需要把待诊断的样本特征向量输入已训练的神经网络即可实现快速诊断。

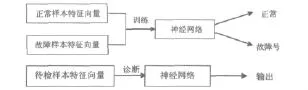
图2 神经网络训练及在线故障诊断过程Fig.2 On-line fault diagnosis and training process of neural network

3 实例诊断

为了应用本文所提出的诊断方法，在600 MW超临界汽轮发电机组轴系试验台上进行了试验研究，采集了转子正常、转子不平衡故障、转子不对中故障、汽流激振故障、轴承松动和动静碰磨6种状态各50个启停机振动数据。图3所示为600 MW超临界汽轮发电机组轴系和动力系统实物图。每个轴承座均安装BENTLY 3 000XL8 mm电涡流传感器，输出为7.87 V/mm，在实验过程中，采样频率为转速的32倍，每个样本数据采集1 024个数据，实验时转子最高工作转速为3 200 r/min。图4～图9分别为6种状态下的三维谱图。

图3 600 MW超临界汽轮发电机组轴系实验台Fig.3 Rotor-bearing system test-bed of 600 MW Supercritical steam unit turbine

图4 转子正常振动三维谱图Fig.4 3-D spectrum of normal rotor vibration

图5 转子不平衡故障振动三维谱图Fig.5 3-D spectrum of rotor unbalanced fault vibration

图6 转子不对中故障振动三维谱图Fig.6 3-D spectrum of rotor misalignment fault vibration

图7 汽流激振振动三维谱图Fig.7 3-D spectrum of steam exciting vibration fault

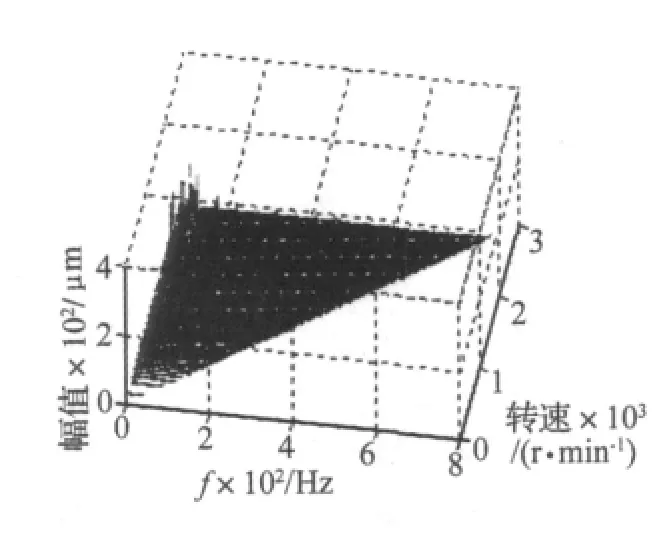
图8 轴承松动故障三维谱图Fig.8 3-D spectrum of bearing pedestal looseness

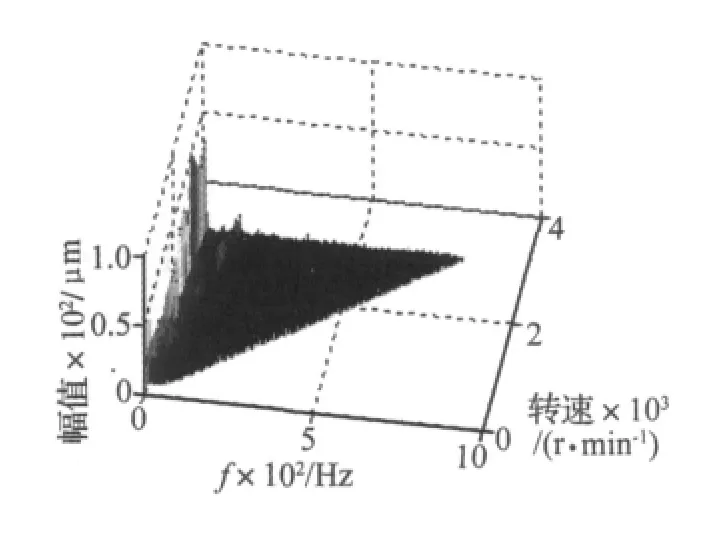
图9 动静碰磨故障三维谱图Fig.9 3-D spectrum of contact rubbing

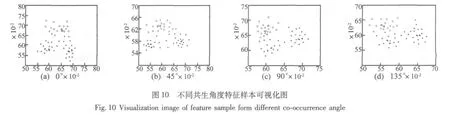
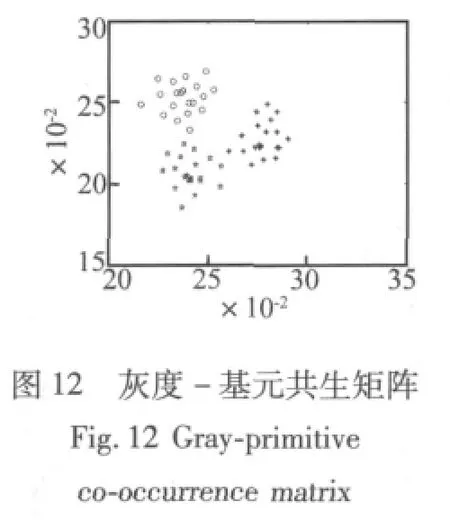
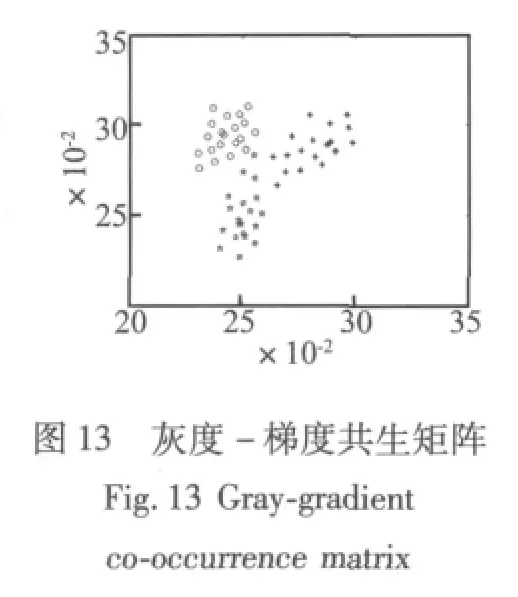
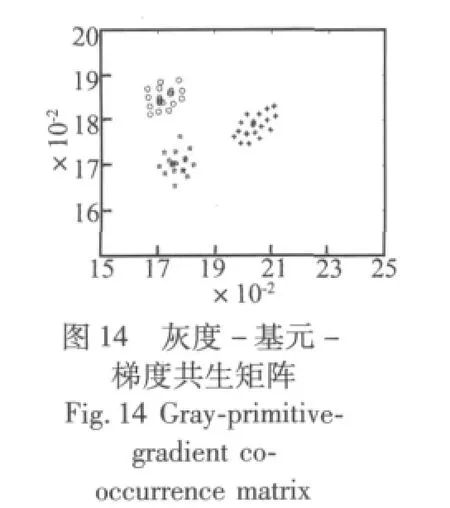
为了验证本文的三维共生矩阵图形特征提取方法的有效性，本文依次利用灰度共生矩阵、灰度-基元共生矩阵、灰度-梯度共生矩阵以及本文提出的灰度-基元-梯度共生矩阵提取图形特征。下面以正常状态、不平衡故障和轴承松动的三维图形样本各20个为例进行图形特征提取。本文中图形选取最大灰度级别为64，图 10 是三种样本提取其 0°、45°、90°、135°共生矩阵后的特征二维可视化图形，由于从共生矩阵中提取的多维统计特征无法在二维空间法描其分类特性，为此，本文利用人工免疫能量降维法［13］，在保证多维分类数据的类别特性的基础上对多维数据进行降维处理。图中“○”表示降维后的正常样本，“☆”表示降维后的不平衡样本，“*”表示降维后的轴承松动样本。从图中可以清楚的看出同类的样本具有明显的聚类性，共生角度不同，降维空间分布略有不同，且不同类别样本在与其他样本混合分布区域有明显的类别交叉样本，这些样本在诊断时往往很难进行准确的分类，但同类样本的聚类性基本不变。考虑到共生角度的影响图11给出了融合共生矩阵［11］提取的特征图，从图中可以看出不同状态特征的聚类分布性较好，混合交叉分布的样本较少，利用这样的样本特征进行诊断有利于诊断精度的提高。同样图12和图13给出灰度-基元共生矩阵和灰度-梯度共生矩阵三种样本的二维特征图，从图中可以看出三种共生矩阵特征分布明显不同，灰度-基元共生矩阵和灰度-梯度共生矩阵同样存在样本混合分布区域交叉现象，但是灰度-基元-梯度三维共生矩阵的样本就没有混合交叉分布样本，利用这样的样本特征进行故障诊断可以获得较高的诊断精度。

获取了图形的特征向量以后就可以利用人工神经网络进行故障识别。本文中利用每种状态的前20个样本特征训练神经网络，剩下的30个样本进行诊断测试，训练后的神经网络即可进行诊断，结果用灰度-基元-梯度共生矩阵图形特征诊断准确率达到85%以上，6种状态的30个测试样本分别错分了1个，3个，4个、3个、4个和 2个，诊断准确率为 96.7%，90.0%，86.7%，90.0%，86.7%和 93.3%，由此可以得出，人工神经网络具有较好的分类效果。也证明了本文所提出的基于灰度-基元-梯度共生矩阵图形特征提取方法的可行性。

为了进一步验证灰度-基元-梯度共生矩阵能有效地提取灰度图形特征，本文用同样训练和测试样本进行了融合灰度共生矩阵、灰度-基元共生矩阵和灰度-梯度共生矩阵的统计特征提取。为了利用上文建立的神经网络，故在共生矩阵中提取统计特征时统一用6个特征描述图形，诊断结果见表1。从表中可以看出基于灰度-基元-梯度共生矩阵的诊断准确率高于其他方法，从而验证了本文提出的灰度-基元-梯度共生矩阵提取旋转机械参数图形特征的有效性。

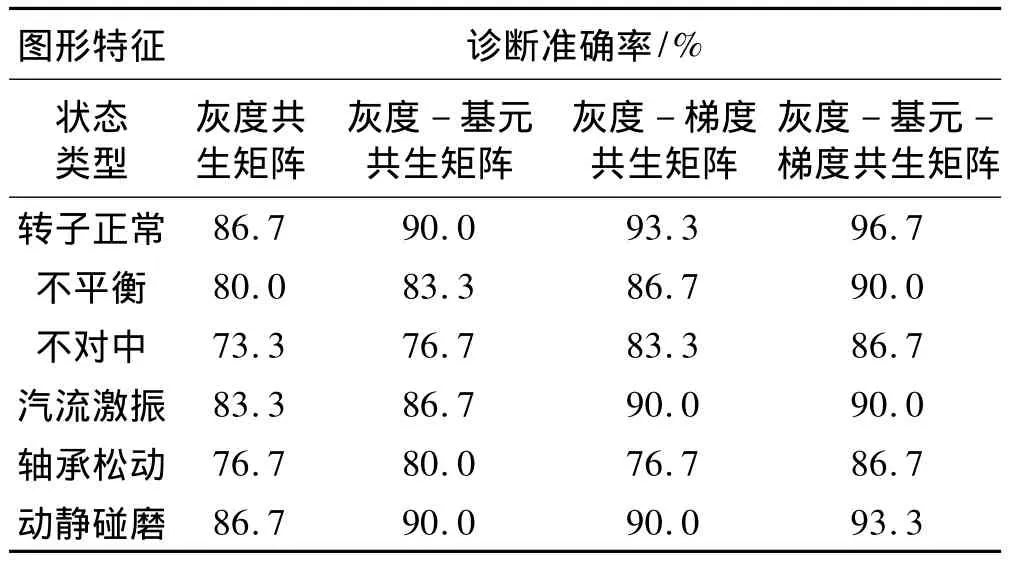
表1 诊断结果统计表Tab.1 Statistics of fault diagnosis result

4 结论

以旋转机械振动状态参数图形为研究对象，依据图形识别技术提出了直接提取和挖掘旋转机械状态参数图形中特征信息的灰度-基元-梯度共生矩阵方法，给出了三维灰度-基元-梯度共生矩阵的概念，对比了灰度共生矩阵、灰度-基元共生矩阵和灰度-梯度共生矩阵图形特征的诊断结果，本文方法可以获得较高的准确率，通过实验验证了该方法能较好地实现旋转机械故障诊断。

［1］冯志鹏，宋希庚，薛冬新.旋转机械振动故障诊断理论与技术进展综述［J］.振动与冲击，2001，20(4):36-41.

［2］Zhan Y M，Makis V.A robust diagnostic model for gearboxes subject to vibration monitoring［J］.Journal of Sound and Vibration，2006，290(3-5):928-955.

［3］Cho S J，Kim J H.Bayesian network modeling of strokes and their relationships for on-line handwriting recognition［J］.Pattern Recognition，2004，37:253-264.

［4］Yang B S，Han T，An J L.ART-KOHONEN neural network for fault diagnosis of rotating machinery［J］.Mechanical Systems and Signal Processing，2004，18:645-657.

［5］褚福磊，李贵三，张正松.旋转机械常见故障的振动三维谱特征及其识别［J］.清华大学学报，1996，36(7):86-91.

［6］吴峰崎，孟 光，荆建平.基于声信号三维谱分析的转子复合碰摩故障特征提取［J］.振动与冲击，2005，24(6):79-85.

［7］史东锋，屈梁生.轴心轨迹定量特征提取技术在回转机械诊断中的应用［J］.化工机械，1998，26(1):25-31.

［8］ Li Z，Chen X C，Zhang Z R，et al.Application of image processing to diesel fault vibration diagnosis［J］.Journal of Vibration Measurement＆ Diagnosis，2002，22:300-305.

［9］窦 唯，刘占生，马晓峰.旋转机械故障诊断的灰度-基元共生矩阵方法研究［J］.航空动力学报，2008，23(9):1609-1616.

［10］窦 唯，刘占生.基于灰度-梯度共生矩阵的旋转机械振动时频图形识别方法［J］.振动工程学报，2009，22(1):85-91.

［11］刘占生，窦 唯.基于旋转机械振动参数图形融合灰度共生矩阵的故障诊断方法［J］.中国电机工程学报，2008，28(2):88-95.

［12］王惠明，史 萍.图像纹理特征的提取方法［J］.中国传媒大学学报，2006，13(1):49-52.

［13］ Tarakanov A. Mathematical models of bio-molecular information processing:formal peptide instead of formal neuron［J］.Journal of Problem of Information，2001，1(2):46-51.