基于改进人工鱼群算法的机械故障聚类诊断方法

陈安华，周 博，张会福，文 宏

（1.湖南科技大学 湖南省机械设备健康维护重点实验室，湖南 湘潭 411201；2.湖南科技大学 知识处理与网络化制造湖南省普通高校重点实验室，湖南 湘潭 411201）

在复杂设备的状态监测信号中必然包含各种复杂联系，而这些复杂的联系对应着不同的故障类型。当前应用于机械故障诊断的逻辑推理分类方法常见的有人工神经网络、贝叶斯分类、遗传算法和决策树、粗糙集理论、蚁群聚类等［1-6］。而常规逻辑推理方法难以从大量的测试数据中既快又准地诊断出被测系统测试数据中的故障类型。发展新的理论或方法快速准确地实现机械故障信号的聚类诊断是众多学者研究热点。

人工鱼群算法是李晓磊等［7］提出的一种基于动物自治体的自下而上设计的新型寻优策略，该算法模拟了自然界中鱼群的觅食、聚群、追尾行为。由于人工鱼群算法具有结构简单、良好的并行性、快速性等特点被应用于传感器网络增强及电力系统的无功优化、最优潮流计算、短期负荷预测、系统在线辨识、前向神经网络优化等领域［8-9］。人工鱼群算法是在人工鱼所处环境的食物浓度及拥挤度的引导下来实现鱼的聚群与追尾，最终实现所有人工鱼聚集在几个极值中心周围。机械故障特征信号聚类是故障样本在相似度因子及聚类判别因子的引导下，使得所有的故障样本聚集在几个极值样本附近，实现故障的聚类诊断。这两者过程极为相似，因此本文把人工鱼群算法应用于机械故障诊断中，建立了基于鱼群追尾行为的故障聚类诊断模型，通过故障聚类诊断仿真，验证了该方法的有效性。

1 人工鱼群算法

自然中鱼的生活习性为：在食物浓度的引导及对该区域鱼群是否拥挤判断的前提下，通过自行或尾随其他鱼等行为找到营养物质最丰富的地方，即鱼生存数目最多的地方就是水域中富含营养物质最多的地方。人工鱼群算法就是通过模拟鱼的觅食行为、聚群行为、追尾行为自下而上设计的寻优算法，在食物浓度等引导下，通过觅食、聚群、追尾行为使得人工鱼最终聚集在几个局部极值点附近。

1.1 人工鱼模型的定义［7］

个体鱼的状态为X=（x1，x2，x3，…，xn），其中xi（i=1，2，3，…，n）为各寻优变量；人工鱼当前所在位置的食物浓度为Y=f（X），其中Y为目标函数值；dij表示鱼群中个体鱼之间的距离；visual表示个体鱼的视野范围；step表示个体鱼的移动步长；δ表示拥挤度因子。

1.2 人工鱼群算法的基本原理［7］

觅食行为：设人工鱼当前的状态为Xi，在该个体鱼的视野范围内随机选择一条状态为Xj的人工鱼，如果Xj周围的食物浓度Yj大于Xj周围的食物浓度Yi，则Xi向Xj移动一步；否则，再重新随机选择Xj，判断是否满足条件，反复几次后如仍不满足条件，则随机移动一步。

具体应用中可根据问题的需要只采用其中的一种或几种行为。

通过上述行为可以看出，人工鱼群算法的基本原理就是人工鱼在食物浓度的引导下，当选择的食物源处鱼不拥挤时，人工鱼就游向该食物源，最终实现人工鱼都聚集在几处食物浓度较大的食物源附近。

2 改进人工鱼群追尾聚类算法及其在故障聚类诊断中的应用

2.1 基本原理

2.2 改进的人工鱼群追尾聚类算法

（1）初始化鱼群：每条人工鱼都作为一个独立的群；Y为食物浓度；人工鱼的可视范围为visual；给定拥挤度因子δ；step为移动步长；d为鱼群间的距离。

（2）随机选择一条人工鱼Xi，找出其可视域内的食物浓度最大的鱼群中心Xj；

（3）如果存在多处最大值则随机选择一个鱼群中心Xj，并以Xj作为中心找出除Xi以外的食物浓度最大的鱼群中心Xk，若食物浓度满足Yi＞Yk，则把Xi作为中心，否则把Xj作为中心；

（4）若以Xi为中心，判断Xj周围的拥挤度是否小于设定的拥挤度因子δ，如果小于（即满足追尾条件）则Xj向Xi移动步长step（即Xi和Xj聚为一类），聚类中心为Xi；如果不满足追尾条件，判断是否达到设置迭代最大值，若未达到，则返回（3）继续执行；若达到，则返回（2）继续执行；

（5）判断是否所有人工鱼都找到了各自的聚类中心，如果未完成则返回（2）继续执行；

（6）输出各聚类中心。

由于该算法是一个无导师学习过程，可设置迭代次数作为算法的终止条件。

2.3 相似度因子及聚类判别因子的定义

设X=（x1，x2，…，xn）为样本的故障特征向量，定义两样本间的相似度因子为两样本间的欧氏距离的倒数即：

其中，Xik为故障样本Xi的第k个特征；Xjk为表示故障样本Xj的第k个特征；Yij为故障样本Xi和Xj间的相似度因子。

由式（1）可知Xi和Xj欧氏距离越小表明两故障样本为同一故障的概率越大，即Yij越大表示两故障样本的相似度越高。但当某些特征量变化较大时使得欧氏距离在样本分类时误差变大，为减小因某些特征量变大而引起分类误差，本文引入了向量夹角的余弦，向量夹角的余弦值能够反映特征值内部的变化。因此本文把故障样本间夹角的余弦值作为聚类判别因子，由余弦定理公式，两样本夹角的余弦值为：式中：Xik为故障样本为Xi的第k个特征；Xjk为故障样本为Xj的第k个特征；θ为故障样本间的余弦角；hij为故障样本Xi和Xj间的聚类判别因子。

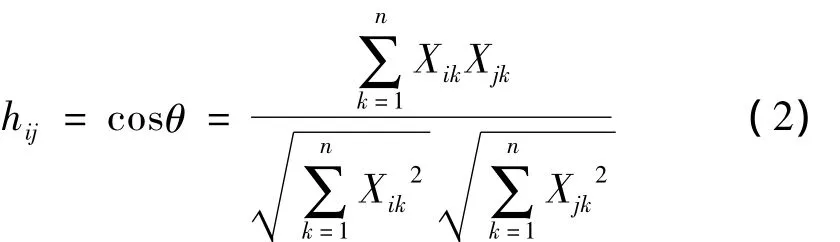
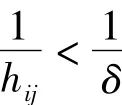
2.4 基于改进人工鱼群追尾聚类算法的故障聚类诊断模型

首先对采集的数据进行预处理，按照一定的规则把数据形成鱼群追尾算法能够处理的测试数据样本，然后对预处理后的数据进行故障聚类及模式识别。基于人工鱼群追尾聚类算法的故障聚类诊断模型描述如图1所示。

图1 基于改进人工鱼群追尾聚类算法的故障聚类诊断模型Fig.1 The model of clustering in mechanical fault diagnosis based on improved fish-swarm algorithm

3 实例分析

为了较直观的体现该算法与其他算法效果的优劣，本文采用文献［10］中往复机械（柴油机）的供油系统的故障诊断为例，表1所示为运行历史数据形成的故障诊断决策系统。

其中，U={1，2，…，10}表示柴油机油路系统的10个故障状态；k表示各故障状态对应的样本数。C={a，b，c，d，e，f}表示柴油机油管压力波形特征的 6 个征兆属性集合，a表示喷油起点油管的残余压力；b表示最大喷油压力；c表示二次喷射压力；d表示喷射压力第三峰值；e表示压力升高率；f表示喷油提前角。在故障征兆属性a，b，e，f的取值中：0表示降低；1表示不变；2表示增高。在故障征兆属性c，d的取值中：0表示无；1 表示有。g={1，2，3，4，5，6}表示柴油机油路系统的故障类别：1表示喷油器针阀故障；2表示供油提前或滞后；3表示喷油压力异常；4表示供油量异常；5表示出油阀针面磨损；6表示油管接头处漏油。

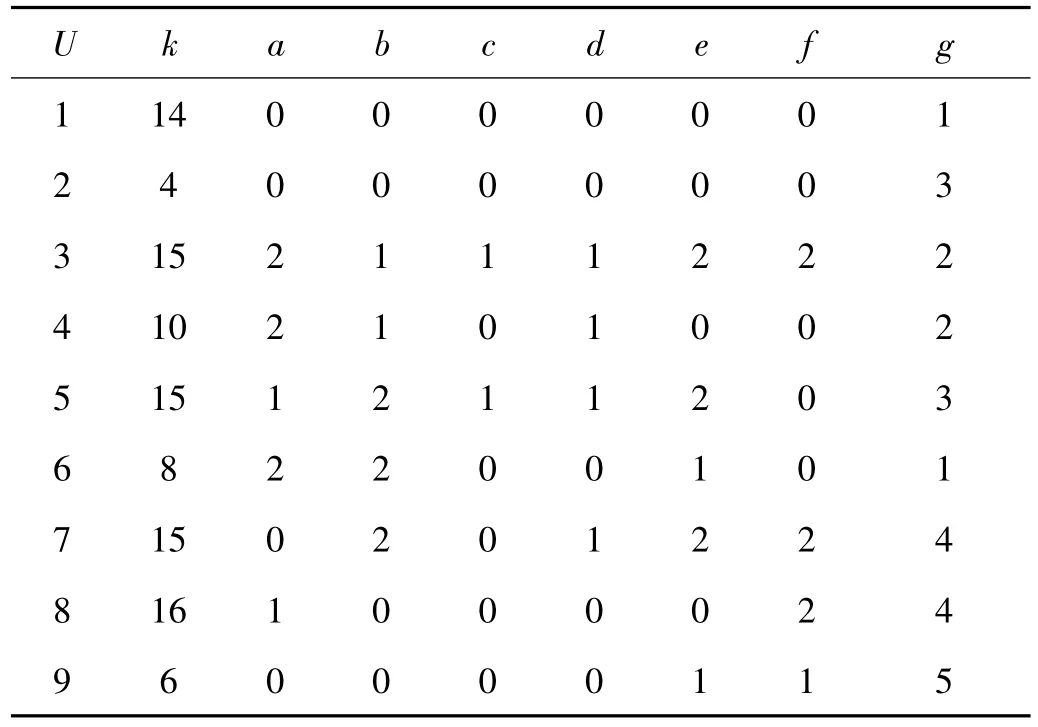
表1 原始故障诊断决策表Tab.1 The decision table of initial fault diagnosis

把上述106个样本中选出包含所有故障的30个样本作为测试样本，剩余的76个样本作为训练样本。在76个训练样本中以20个样本数据为一组随机选取了三组作为训练样本，在30个测试样本中以10个样本为一组随机选取三组作为测试样本，算法中移动步长取值为step=1，当取不同的聚类判别因子时，得出了图2所示的三条聚类判别因子与诊断正确率的关系曲线。

图2 聚类判别因子与诊断正确率Fig.2 Discriminant factor and diagnosis rate

图2中横坐标表示聚类判别因子，纵坐标表示整体故障诊断正确率；由图2知当判别聚类因子取值为δ=0.95时正确率最高，因此本文实验均取聚类判别因子为δ=0.95。

为直观的了解该方法的效果，做如下实验随机选取76个训练样本中的40个数据作为训练样本，在30个测试样本中选取了包含6种故障的10个数据样本作为测试样本（表2），设置训练样本的迭代次数为30，对训练样本做训练，然后对测试样本做的测试。

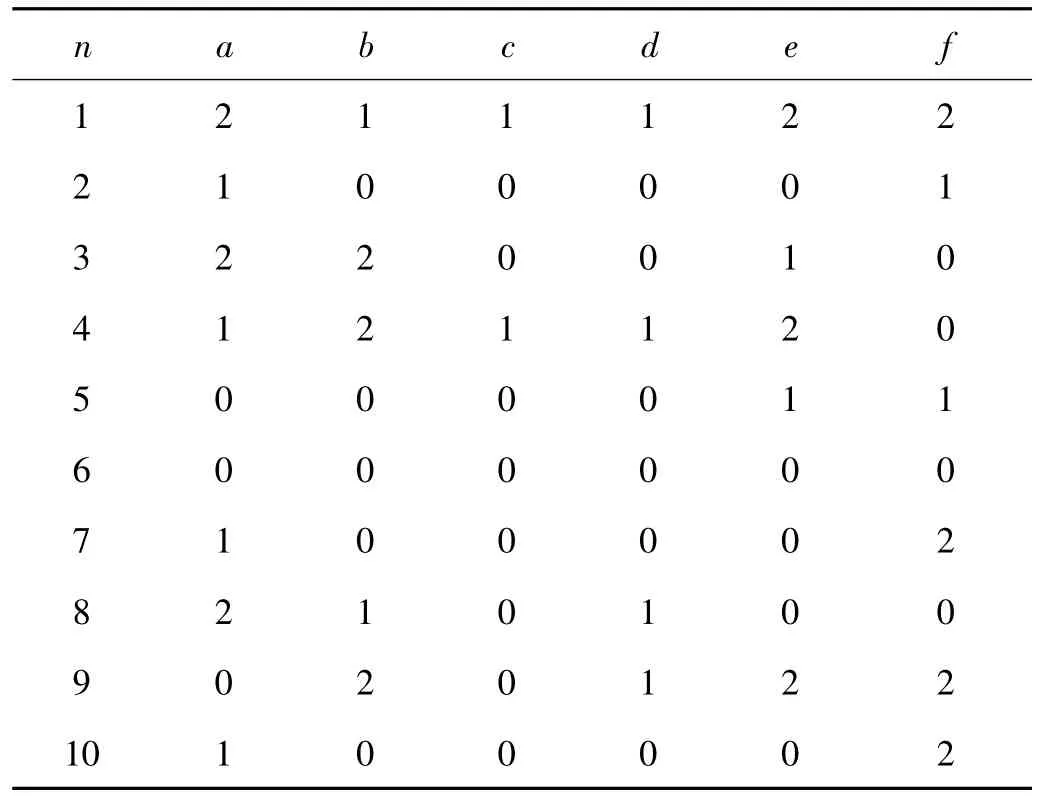
表2 测试样本数据Tab.2 Data of text sample

表2中，n表示测试样本编号，测试结果如表3所示。

表3 测试样本分类表Tab.3 The classification table of text sample

表3中n表示测试样本的编号，g表示的是样本所对应的故障类别。在样本数为10时，迭代30次整体的故障诊断正确率在90%。表4给出了训练样本为60，测试样本数目为30，迭代次数分别取20，50，70时三组测试样本的测试结果。

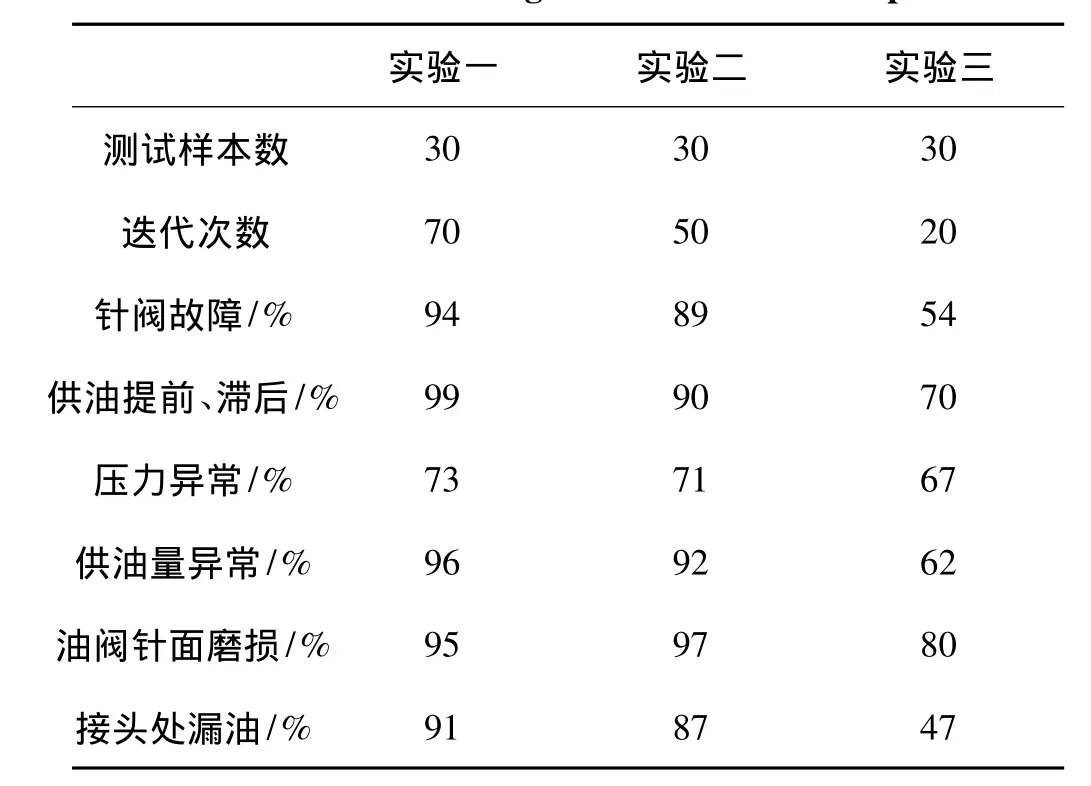
表4 测试样本各故障诊断正确率表Tab.4 The fault diagnosis rate of text sample

表4所示为不同迭代次数该算法所得出的各故障的正确率。由表4可知，对同一样本当设置的迭代次数不同时，各故障的诊断正确率也不同，当迭代次数为70时，所有故障的平均诊断正确率达到91%以上。迭代次数与整体故障诊断正确率得关系，如图3所示。

图3 迭代次数与整体正确率Fig.3 Iterations ＆ overall accuracy

图3中横坐标表示的是在测试样本为30时，设置的迭代次数；纵坐标表示的是与迭代次数对应的整体故障诊断正确率。由图3反映出随着迭代次数的增加整体故障诊断正确率也随之增高，当迭代次数达到70时正确率达到最大值，诊断正确率不再随着迭代次数的增加而增高。

在76个训练样本中随机选取60个数据样本作为训练样本，重复三次，得到三组不同的训练样本，然后分组对30个测试样本进行测试，迭代次数为70时该算法的三组诊断结果均值与文献［11］中算法的最终结果比较，如表5所示。

表5 改进人工鱼群追尾聚类算法、RS＆PCA、遗传算法的比较Tab.5 The comparison result of RS＆PCA，genetic algorithm and improved fish-swarm algorithm

表5可知，改进人工鱼群追尾聚类算法的故障样本诊断正确率高于RS＆PCA和遗传算法，正常样本的诊断正确率和整体正确率都高于遗传算法。但正常样本和整体正确率低于RS＆PCA算法。

4 结论

本文结合人工鱼群算法的特点，模拟人工鱼群追尾行为提出了改进的人工鱼群追尾聚类算法，在此基础上发展了一种基于人工鱼群追尾聚类算法的机械故障聚类诊断的新方法，通过与遗传算法和RS＆PCA算法比较可知能达到较好的故障诊断效果。该算法不需要提前定义聚类组数，能够对特征变化不确定的故障提供有效的判别依据。但该算法还存在进一步完善的空间，主要在迭代次数及拥挤度因子的选取上，如何实现针对不同数据能自适应地选取迭代次数和拥挤度因子是有待深入研究的问题。

［1］陈 果.粗糙集-遗传算法-神经网络集成分类器及其在转子故障诊断中的应用研究［J］.中国机械工程，2008，19（1）：85-90.

［2］ Zhou Q M，Yin C B，Li Y S.Application of variable precision rough set model and neural network to rotating machinery fault diagnosis［J］.Lecture Notes in Computer Science，2005，3642：575-584.

［3］杨昌昊，竺长安，胡小健.基于贝叶斯网的复杂系统故障诊断方法［J］.中国机械工程，2009，20（22）：2726-2732.

［4］Sakthivel N R，Sugumaran V，Nair B B.Comparison of decision tree-fuzzy and rough set-fuzzy methods for fault categorization of mono-block centrifugal pump［J］.Mechanical Systems＆ Signal Processing，2010，24（6）：1887-1907.

［5］ Zhang Y Z，Shi L S，Qin L.Rolling bearings fault diagnosis based on adaptive genetic algorithm and spectral kurtosis algorithm［J］.Bearing，2010（3）：27-32.

［6］ Zhang X L，Chen X F，He Z J.Fault diagnosis based on support vector machines with parameter optimization by an ant colony algorithm［J］.ProceedingsoftheInstitution of MechanicalEngineers. PartC， Journalofmechanical engineering science，2010，224（1）：217-229.

［7］李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法［J］.系统工程理论与实践，2002（11）：32-38.

［8］ Zhang K，Zhang W，Dai C Y，et al.Artifical fish-swarm based coverage-enhancing algorithm for visible light sensor networks［J］.Optoelectronics letters，2010，6（3）：229-231.

［9］何登旭，曲良东.人工鱼群聚类分析算法［J］.计算机应用研究，2009，26（10）：3665-3668.

［10］黄文涛，赵学增，王伟杰，等.基于粗糙集理论的故障诊断决策规则提取方法［J］.中国电机工程学报，2003，23（11）：150-154.

［11］姜万录，刘思远.粗糙集及主元分析的机械故障诊断研究［J］.机床与液压，2009，37（12）：215-218.