飞机噪声计算通用模型研究

刘 洲，蔡良才，方 华，邵 斌，杜宜霖，孙 捷

（1.空军工程大学 工程学院机场建筑工程系，西安 710038；2.环境保护部环境工程评估中心，北京 100012）

随着经济的迅速发展和人民生活水平的不断提高，航空事业也赢来了全新的发展时期，世界各地军用和民用机场建设如火如荼，由此而带来的机场飞机噪声问题也日益突出［1-3］。为确保机场与周边环境的和谐发展，科学地预测新建或改扩建机场飞机噪声的影响范围与强度就显得非常重要。国内外的许多学者对此展开了深入研究［4-7］，探寻飞机噪声的产生机理和传播规律，以期望找到行之有效的噪声预测方法。这些研究大都集中于飞机噪声的基础理论和预测评价量的计算和修正方面，尚没有建立一整套完善的可直接用于实际工程的噪声计算体系。美国INM（Integrated Noise Model，综合噪声模型）软件是一套比较先进的噪声计算软件，其民用部分已经成功的运用于我国民航飞机的噪声评价，军用部分则由于机型、航线和飞行训练等方面的差异，无法直接用于我国军用机场，而且军航和民航分开在一定程度上限制了其在军民合用机场上的运用［8］。

文献［9］中的附录A对飞机噪声环境影响预测和评价的基本程序进行了介绍，给出了评价量的计算公式和相关的附加修正方法。目前的机场飞机噪声环境影响评价大都依此规范进行，但在实际运用过程发现，由于飞行航线多种多样，构造复杂，飞机沿航线飞行时速度、功率、爬升率等飞行状态都在不断变化，其飞行轨迹也有弯道和直线交替变化的现象，噪声计算时如何确定预测点到航线的最短距离，如何考虑飞机不同飞行状态的影响，这就需要有一套完整的可操作性强的计算模型才行，仅仅知道评价量的计算公式无法解决这些技术问题。且传统的计算方法由于缺乏通用的航线模型和规范的数据管理，所建立的飞行航线缺乏通用性，无法适用与其他机场，导致噪声环境影响评价时的重复工作量较大，既费时又费力，且由于大量的计算工作需要人工操作完成，容易出错，增加后期的数据管理难度。

本文在深入分析各种航线特点的基础上，考虑将航线进行分段研究，建立通用的适合各种机型不同航线的噪声计算模型，完善飞机噪声计算体系，规范飞机噪声环境影响评价工作模式，提高工作效率，提高整个评价过程的智能性和科学性。

1 航线分解

分析飞行航线的特点可以发现，任何一条航线，不论是军用飞机航线还是民用飞机航线，不管其构成多么复杂，都可以分解成为许多航线片段（简称航段）的组合，每一片段的速度、功率、飞机仰角等飞行状态相对比较稳定，只要确定了每一片段的轨迹，整个航线就确定了。通过对这些组成片段加以分析，发现其主要有两大类，一类是直线（包括起飞滑跑、着陆滑跑、直线爬升、直线下滑以及直线平飞等）；另一类是曲线（包括左转弯爬升、右转弯爬升、左转弯平飞、右转弯平飞、左转弯下滑、右转弯下滑等）。这两类基本航段就是飞行航线组成的基本要素，其不同的排列组合共同构成了不同的飞行航线。每一要素的几何特征具有相似性，其数学模型基本相同，不同的只是相关参数而已，因此只要建立直线和曲线航段这两个基本要素的通用模型，就可以任意增加删减航段，变换相关参数，组合而成任何所需要的飞行航线。计算出飞机沿各个航线片段飞行时在预测点的噪声，再进行叠加就可以得到整个飞行事件在预测点产生的噪声。假定图1中的航线在如图所示的四段中飞行状态相对稳定，那么噪声计算时就可以将该航线划分成编号为①、②、④的三个直线航段和编号为③的曲线航段，P点的噪声就是各航段对该点的噪声贡献之和。

图1 飞行航线水平投影图Fig.1 Horizontal projection of an air line

2 航线片段通用模型的建立

以跑道中心线的中点为坐标原点，中心线延长线方向为X轴，垂直跑道方向为Y轴，高程用Z轴表示，建立直角坐标系。

2.1 直线航段通用模型

该航线片段示意图如图2、图3所示。

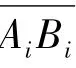
由航线的连续性和传递性可知，第i个航段的起点坐标是第i-1个航段的终点坐标，第i个航段的终点坐标可由相关参数求得：

起点坐标：

终点坐标：

2.1.1 影响区域计算

现行的飞机噪声计算是以飞机噪声距离特性（Noise-Power-Distance，简称NPD）曲线为基础的。NPD数据把噪声级定义为飞机以稳定的功率、恒定的参考速度飞行时，理想无限长的直线航迹上垂直距离的函数，即该噪声级是飞机飞越预测点上空整个过程的综合噪声效应。飞机飞跃一次，预测点就叠加一次噪声。计算该噪声级的关键在于确定预测点到飞行轨迹的最短距离（斜距），以及最短距离位置处发动机功率、速度等飞行状态，然后结合NPD数据插值相应的噪声级。当飞行航线由若干航段表示时，噪声计算就只与飞跃预测点的航段有关。这并不是说其它航段对预测点的噪声没有贡献，而是预测点的噪声计算不需要其他航段的参数信息，事实上这些航段的噪声贡献都已经涵盖在根据飞跃预测点的航段所计算的噪声级里了。因此，对于每个航段来说，其都将存在一个影响区域，若预测点落在影响区域内，则噪声计算与该航段有关，若预测点落在影响区域外，则噪声计算与该航段无关。直线航段的影响区域为该航段平面投影沿其垂直方向运动所覆盖的区域，如图3所示，即为y=k'（xxAi）+yAi和y=k'（x-xBi）+yBi所夹区域。

根据αi取值的不同，影响区域的表达式也不相同。

αi=0时，影响区域为：

αi=π/2时，影响区域为：

αi=π时，影响区域为：

αi=3π/2时，影响区域为：

0＜αi＜π 且α≠π/2 时，由k=tanαi，得k'=-1/k，影响区域为：

π ＜αi＜2π 且α≠3π/2 时，由k=tanαi，得k'=-1/k，影响区域为：

2.1.2 噪声计算

若预测点落在影响区域外，噪声计算与航段无关，为了计算方便，记Ei=0，其中Ei表示第i个航段在预测点的声能量贡献值。若预测点落在影响区域内，如图4所示，则需要计算该航段的噪声贡献值。

首先计算斜距，各参量计算如下：

图4 预测点落在影响区域内Fig.4 The point inside the coverage

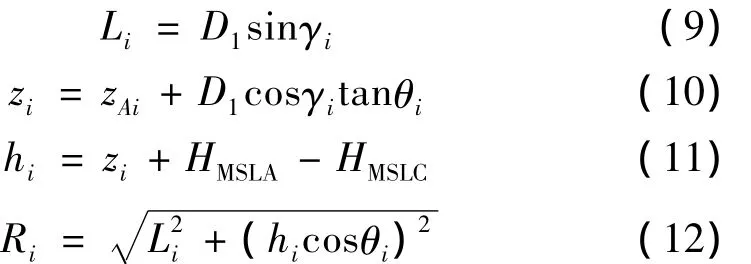
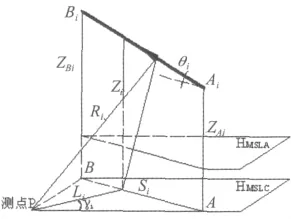
图5 直线航段斜距计算示意图Fig.5 Distance calculation between the point and straight segment

式中：D1，D2，D3分别为点PAi，PBi，AiBi之间的平面投影距离（如图5所示）；Li为预测点到航线的水平距离；zi为飞机相对于机场的飞行高度；hi为飞机相对于预测点的飞行高度；HMSLA为机场海拔高程；HMSLC为预测点海拔高程；Ri为斜距；各符号的具体意义见图5；

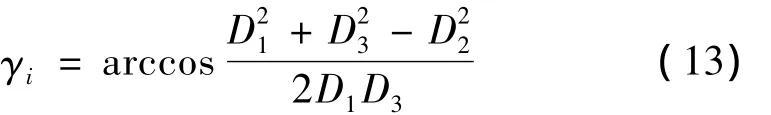
根据斜距和NPD数据，插值可得到预测点初始有效感觉噪声级，记为LEPN0i，也可将斜距代入NPD回归曲线方程计算LEPN0i。NPD数据描述的是噪声级、发动机功率和斜距三者之间的关系，为了应用方便，通常将功率相对固定，求得某些特定功率条件下飞机噪声级和斜距之间的关系式，再在功率之间线性插值来修正功率对噪声级的影响。曲线方程通常采用二次多项式拟合［10］，即某功率条件下噪声级和斜距之间的关系为：

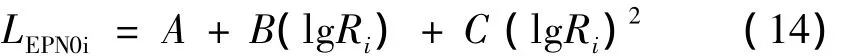
式中：A、B、C为拟合所得的某种飞机的噪声距离特征曲线系数。

由于飞机的飞行线路、发动机推力、速度等飞行状态都在不断变化，因此就需要对LEPN0i值进行修正。修正包括速度修正、温度和湿度修正、侧向衰减修正等。修正时预测点相应功率和速度的计算按距离线性内插计算。修正方法文献［9］附录A已有介绍，这里不再赘述。经过修正最终得到飞机沿该航线片段飞行时预测点的有效感觉噪声级LEPNi，其声能量贡献值为：

2.2 曲线航段通用模型

该航线片段示意图如图所示：

与直线航段相似，完整描述该航段模型并计算飞机沿该航线片段飞行时的噪声所需要的参数有航段序号i，飞行航迹水平夹角θi（爬升角为正，下滑角为负，平飞为零），末端高度zBi，航线的水平转角αi（0＜αi＜π），转弯半径ri，末端速度vBi，末端功率wBi以及转弯中心的平面坐标Oi∶（x0i，y0i）等。

起点坐标：

终点坐标：

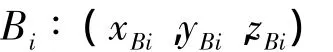
其中：

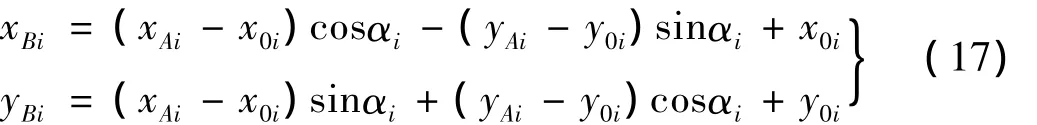
2.2.1 影响区域计算

水平投影面内，曲线航段取圆弧两端点与圆心之间的连线所夹的区域为影响区域，如图7所示，令kA=（yAi-y0i）/（xAi-x0i），kB=（yBi-y0i）/（xBi-x0i），根据Oi、Ai、Bi不同的位置关系分以下四种情况：

当x0i=xAi时，影响区域为：

当x0i=xBi时，影响区域为：

当（x0i-xAi）（x0i-xBi）＞0时，影响区域为：

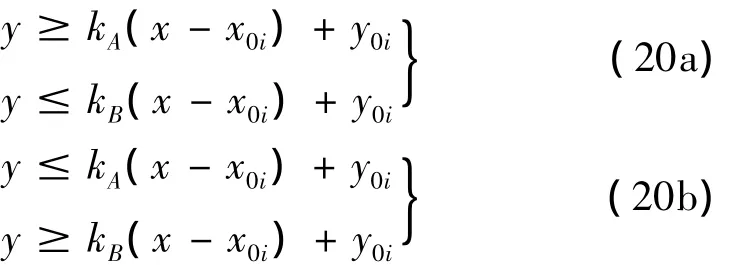
当（x0i-xAi）（x0i-xBi）＜0时，影响区域为：

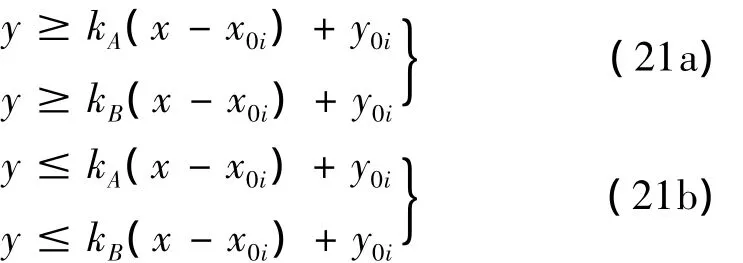
2.2.2 噪声计算

同直线航段一样，噪声计算之前，需要判断测点是否落在影响区域内，若不在则取Ei=0，若在则按与直线航段相同的步骤计算预测点的噪声。由于曲线航段的影响区域为两个扇形区域，测点落在不同的扇形区域时，其斜距计算公式略有差别，计算前需要先判断预测点的位置属于哪一种情况，如图8所示。

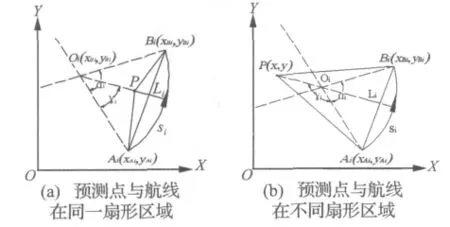
图8 预测点位置示意图Fig.8 Different location of the point

当预测点与航线在同一扇形区域时，斜距计算按图9（a）进行，各参量如下：

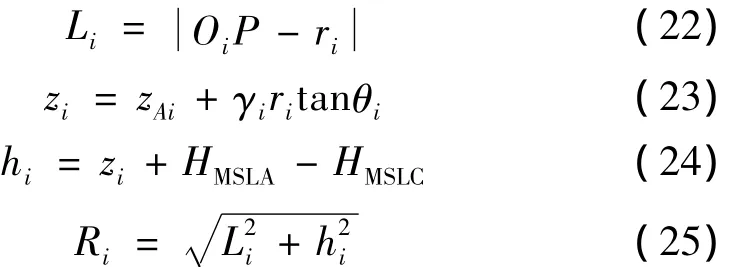
图9 曲线航段斜距计算图Fig.9 Distance calculation between the point and curve segment

当预测点与航线在不同扇形区域时，斜距计算按图9（b）进行，各参量如下：

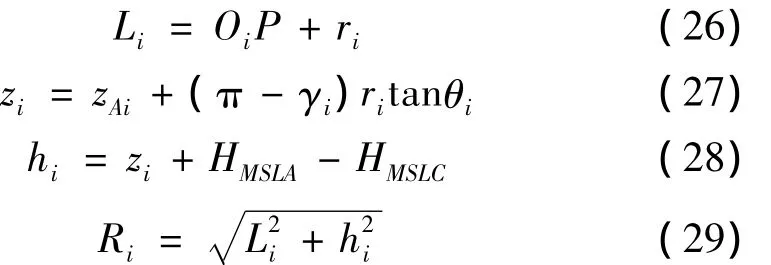
其中：OiA、OiP、AP为两点之间的距离。

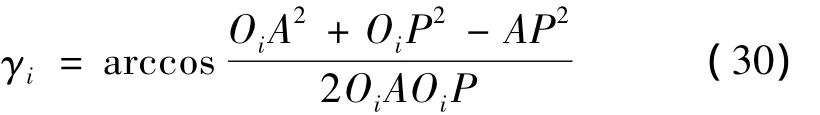
将斜距代入NPD回归曲线方程计算LEPN0i并加以修正最终得到飞机沿该航线片段飞行时预测点的有效感觉噪声级LEPNi及其声能量贡献值Ei。

3 单次飞行在预测点的噪声计算

由于航线是由一系列状态相对稳定的直线和曲线航段共同组成的，根据每个航段的输入参数以及前面建立的通用数学模型，可以分别求得每个航段对预测点的噪声能量贡献值。只要把所有航段相对于预测点的噪声叠加就得到飞机沿整个航线单次飞行时在预测点的噪声能量值。

将能量换算成声压级的形式就得到飞机单次飞行的有效感觉噪声级LEPN。

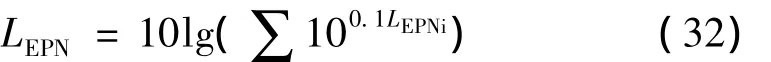
注：计算时航线片段第一段需要指定起点坐标，也就是航线的起始点坐标。

4 应用实例

如图10所示的一条航线供某型飞机离场使用，根据飞机沿航线的飞行状态将其分成四个航段，各航段的飞行参数见表1。

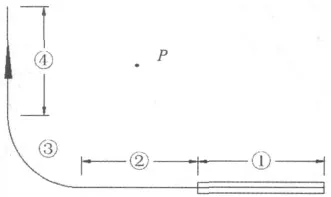
图10 某离场航线示意图Fig.10 Schematic diagram of a departure procedure

表1 航线各航段的飞行参数统计表Tab.1 The flight parameters of each segment

预测点P的坐标为（-4 500，5 500），机场海拔高度124 m，预测点海拔高度126 m，根据空军工程大学工程学院机场建筑工程系的实测资料，拟合出该飞机在不同发动机推力条件下的噪声距离特性曲线公式如下：

推力为23 500磅时，

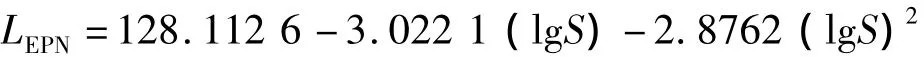
推力为18 000磅时，

要计算该飞机沿航线单次飞行时在P点的噪声，就要分别计算各航段对P点的噪声影响，最后进行叠加。采用本文提出的方法进行计算，结果如表2：

表2 航线各航段噪声计算结果Tab.2 Noise calculation result of each segment

将各航段对预测点P的噪声影响累积，就可以得到飞机沿整个航线单次飞行时的噪声能量值和有效感觉噪声级，E=0+96 105+40 761+52 091=188 957 dB，LEPN=10lg（188 957）=53 dB。

5 结论

本文针对现行飞机噪声计算方法的不足之处，从飞行航线的特点出发，提出“直线段”和“曲线段”这两个基本的航线元素，把航线看作是一系列飞行状态相对稳定的直线和曲线片段的排列组合，飞机沿航线单次飞行时预测点的噪声就等于飞机沿各个航线片段飞行时在预测点产生的噪声之和。建立了直线和曲线航段的噪声计算通用模型，并通过实例验证了该模型的可行性和实用性。本模型具有以下优点：

（1）科学性。模型考虑了飞机沿航线飞行时飞行状态和飞行轨迹的变化，解决了实际噪声计算过程中的相关技术问题，使得整个计算体系更完善，更科学。

（2）通用性。适用于任何航线任何航段，只需要输入航线各阶段的飞行参数，就能自动生成整个航线模型，并进行噪声计算，更智能，更实用。

（3）规范性。航线的生成、模型的计算都可以实现参数化输入输出，容易编程实现，计算过程更规范，数据管理更有效。

（4）可扩展性。本模型可用于计算单次飞行噪声，也可进一步拓展计算多个飞行事件的噪声，满足对整个机场的噪声环境影响评价要求。

［1］ Thomas C S，Hume K I，Hooper P D.Aircraft noise，airport crowth and regional development［J］.American Institute of Aeronautics and Astronautics，2004，2806：477-488.

［2］ DfT.The future development of Air transport in the united kingdom：south east［M］.London：A National Consultation.Department for Transport，2002.

［3］钱炳华，张玉芬.机场规划设计与环境保护［M］.北京：中国建筑工业出版社，2000.

［4］ Ionescu A C，Dumitrescu H.Aircraft noise modeling and noise perception through CDA procedure，the Impact on Communities［J］.American Institute of Aeronautics and Astronautics，2009，3399：220-226.

［5］ Zaporozhets O L，Tokarev V I.Aircraft noise modelling for environmental assessment around airports［J］.Journal of Applied Acoustics，1998，55（2）：99-127.

［6］Farassat F，Casper J H.Towards an airframe noise prediction methodology：survey of current approaches［J］.American Institute of Aeronautics and Astronautics，2006，210：170-182.

［7］ ICAO.CIRCULAR 205-AN/1/25.Recommended method for computing noise contours around airports［S］.Montreal，1988.

［8 ］ Dinges，Hemann，Rickel，et al.Integrated Noise Model（INM）Version 7.0 User＇s Guide［R］.Washington，D.C.：Federal Aviation Administration，2007.

［9］HJ/T 87-2002，环境影响评价技术导则-民用机场建设工程［S］.

［10］沈洪艳，刘劲松.机场噪声预测模型及应用实例［J］.河北师范大学学报，2000，24（1）：137-140.