斜距归算成水平距离误差定量分析

郑佳荣，崔有祯，刘俞含

(北京工业职业技术学院，北京 100042)

斜距归算成水平距离误差定量分析

郑佳荣，崔有祯，刘俞含

(北京工业职业技术学院，北京 100042)

基于两点间斜距及投影到椭球上的原理，选取研究数据，设计程序，进一步绘制了误差等值线，研究了随着A、B两点间距离和竖直角的变化，并通过A、B两点间斜距计算水平距离误差W的变化规律。

斜距；水平距离；竖直角；等值线

测距原理是测量两点间斜距并归算到椭球面上。因此，若测区范围较大时,需要考虑地球曲率的影响,不能把地球表面看作平面[1-2]。本文将通过程序设计定量研究两点间斜距、竖直角对两点间水平距离计算的影响，对工程测量中斜距化为水平距离归算具有实际应用意义。

1 两点间斜距归算水平距离原理[2-3]

把地球上任意两点简化为如图1所示A、B两点，AE是过A点的切线，因此，SAE是测量中归算出的水平距离，即

SAE=SABcos(∠BAE)

(1)

式中，∠BAE为AB的竖直角；SAB为A、B两点的斜距。

SAB′=R∠AOB

(2)

A、B两点间水平距离不归算到椭球面上的误差为W，即

W=SAE-SAB′

(3)

其中，式(1)中角度、距离可观测；式(2)中R已知，圆心角∠AOB的弧度可以在△BAO中通过余弦定理和正弦定理计算，即

(4)

(5)

由式(1)—式(3)可以看出，影响误差W的变量为A、B两点间的距离和竖直角。

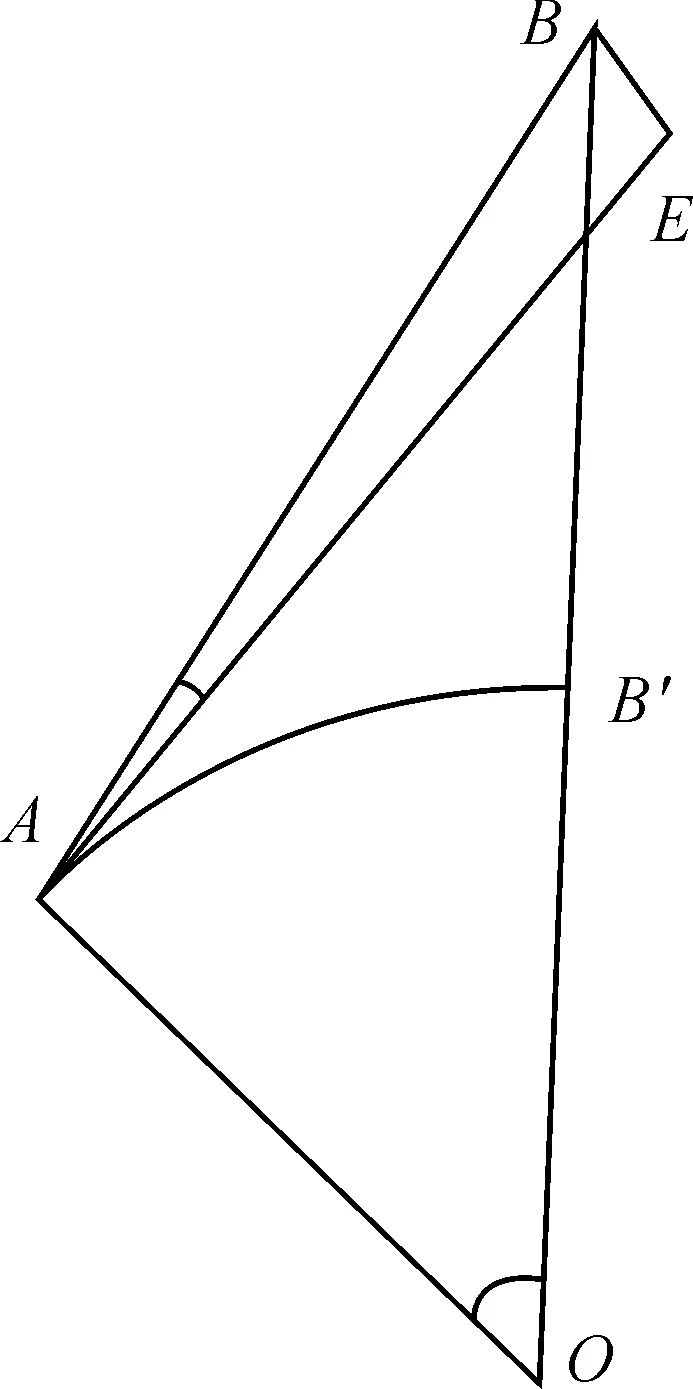
图1 A、B斜距归算平距

2 两点间斜距归算水平距离定量计算

2.1 研究数据及内容

利用两点间斜距归算水平距离的原理，研究随着A、B两点间距离和竖直角的变化，A、B两点间斜距计算水平距离误差W的变化规律。

选取斜距1～10 000 m，间隔为200 m，竖直角0°～3°，间隔为0.05°，计算两点间斜距归算为水平距离的误差W的变化：①相同斜距，随着竖直角变化，W的变化规律；②相同竖直角，随着斜距变化，W的变化规律；③随着斜距、竖直角变化，W的变化规律，见表1。

表1 研究数据

2.2 计算A、B两点间水平距离不归算到椭球面上的误差程序设计及实现

根据两点间斜距归算水平距离原理及设计数据，完成如图2所示算法流程。两个循环嵌套完成斜距从1～10 000 m的循环，竖直角从0°～3°的循环。通过斜距计算A、B两点间水平距离不归算到椭球面上的误差W。

For xj=1 To 10000 Step 200′循环斜距1到10公里

For sj=0 To 3 Step 0.05′循环竖直角0到3度

sj=Round(sj, 2)

sjhd=sj * pi/180′计算竖直角弧度数

pj=xj * Cos(sjhd)′投影面上的平距

q=(90+sj)* pi/180′斜距和半径成的角度

OB=Sqr(xj^2+r^2-2 * xj * r * Cos(q))′点0到B的距离

SinYXJ=xj * Sin(q)/OB′圆心角的正弦值

CosYXJ=Sqr(1-SinYXJ^2)′圆心角的余弦值

TanYXJ=SinYXJ/CosYXJ′圆心角的正切值

jiao=Atn(TanYXJ)′圆心角弧度值

wc=pj-r * jiao′计算距离计算和投影到椭球上弧度之差

Print #1, xj, sj, wc

Next sj

Next xj

图2 AB斜距归算平距流程

3 两点间斜距归算水平距离误差等值线分析

用程序生成数据，距离作为X值(单位km)，角度作为Y值(单位(°))，通过斜距计算的A、B两点间水平距离的误差W作为Z值(单位m)，绘制等值线，生成如图3所示的两点斜距归算水平距离的误差等值线。

图3 两点间斜距归算水平距离w误差等值线

由图3两点间斜距归算水平距离误差等值线可以看出：

(1) 相同竖直角，随着距离增加，通过斜距计算A、B两点间水平距离的误差W递增，竖直角为3°时，斜距为10 km，大于0.7 m。

(2) 相同斜距，随着竖角的增加，通过斜距计算A、B两点间水平距离的误差W递增。

(3) 在水平方向，等值线密度逐渐增加，即随着距离的增大，通过斜距计算A、B两点间水平距离的误差W递增速率加大。

(4) 在竖直方向，等值线密度逐渐增加，即随着竖直角的增大，通过斜距计算A、B两点间水平距离的误差W递增速率加大。

(5) 斜距小于200 m，竖直角小于3°，误差W小于3 mm；距离小于400 m，竖直角小于1°，误差小于3 mm；距离小于600 m，竖直角小于0.4°，误差小于3 mm；距离小于800 m，竖直角小于0.2°，误差小于3 mm；竖直角小于0.05°，斜距小于1400 m,误差小于1 mm；竖直角趋近0°，距离等于10 km，误差约0.02 m。

4 结 论

(1) 竖直角为3°，距离为200 m，误差达到3 mm，因此，当地形不平坦，无论哪一级控制测量计算，其边长的距离改正都不能忽视。

(2) 竖直角趋近0°，量测10 km斜距，投影误差0.02 m，相对误差小于1/500 000，因此，竖角趋近0°，10 km范围内，可以用计算平距代替投影弧长。

[1] 翟翊,魏忠邦,李惠芳. 斜距归算成水平距离的若干问题[J]. 测绘科学技术学报，2009(1):5-7.

[2] 翟翊, 赵夫来.现代测量学[M].北京:测绘出版社,2008.

[3] 施一民. 电磁波测距边归算至投影面的公式论证及应用讨论[J]. 测绘通报，2000(12):6-7.

[4] 王勃慧.全站仪及测距全站仪使用方法浅谈[J]. 西部探矿工程，2008(3):130-133.

[5] 魏忠邦,翟翊. 光电测距水平距离的计算[J]. 测绘通报，2005(9):61-62.

[6] 张高兴.全站仪长距离测量的计算方法及精度研究[J]. 龙岩师专学报，2003(6):64-65.

[7] 北京市测绘设计研究院.城市测量规范：CJJ8—1999[S].北京:中国建筑工业出版社,1999.

[8] 沈洪,施明利,朱军.VB程序设计[M].北京:清华大学出版社,2010.

[9] 王珍.距离归化改正在地铁精密导线测量中的应用[J].工程勘察，2010(S1):670-676.

[10] 孙燕.竖角对光电测距的影响[J].地理空间信息，2005(6):55-58.

Quantitative Analysis of the Calculated Horizontal Distance by Slope Distance

ZHENG Jiarong，CUI Youzhen，LIU Yuhan

(Beijing Polytechnic College, Beijing 100042, China)

Based on the principle of the oblique distance between two points, this paper selects the research data, designs procedure and calculates the difference between the calculated horizontal distance by slope distance and the projection distance to the ellipsoid. Further, the error contour is drawn, and the variation of the horizontal distance error with the variation of the distance between two points and the vertical right angle is studied.

slope distance；horizontal distance；vertical angle；contour line

郑佳荣，崔有祯，刘俞含.斜距归算成水平距离误差定量分析[J].测绘通报，2017(2)：95-97.

10.13474/j.cnki.11-2246.2017.0057.

2016-05-04

北京市教育委员会2015年度科技计划面上项目(KM201510853005)；北京工业职业技术学院(bgzyky201604)

郑佳荣(1979—)，女，博士，副教授，主要研究方向为测绘相关研究及教学。E-mail：zhengjrcumtb@sina.com

P226

A

0494-0911(2017)02-0095-03