声子晶体平板组合成像特性分析

覃世冬，邓芳圆，刘绍娥，李晓春，，周科朝

（1.中南大学 物理科学与技术学院，长沙 410083；2.中南大学 粉末冶金研究院，长沙 410083）

Veselago［1］提出了负折射率的假设。但由于自然界不存在天然的负折射率介质，这方面的研究也就没有得到足够的重视。Pendry等［2-3］利用两种不同金属构成的结构，从理论上实现了GHz频段上负的等效介电常数和负的等效磁导率。实验上，2000年，Smith等［4］同时实现了负的等效介电常数和负的等效磁导率，即得到负的折射率介质。Shelby等［5］在实验上观察到了负折射现象。Pendry［13］关于负折射介质平板可以突破衍射极限、实现完美成像的建议，更是激起了科学工作者的空前兴趣。负折射现象研究也从光子晶体［6-7］扩展到了声子晶体领域［8-11，14-15］。传统的光学透镜及其共轴球面系统成像可以完全地基于单球面正常折射加以解释。声子晶体负折射在引入负折射率后可用反Snell定律描述，但这种描述在成像时，特别是多平板成像过程中，面对实物实像、虚物虚像的复杂情况，是否仍然适用，有必要进行细致的分析。作为声子晶体类似物的光子晶体，也无这方面的详细报道。而且，平板透镜区别于曲面透镜，其独有的成像特性如何也不清楚。针对这些问题，本文以二维声子晶体平板为模型，对声子晶体平板的单板成像和多板成像进行分析，以期更好地认识平板透镜的成像规律，并加深对声子晶体多重散射和负折射之间的贯通理解。

1 基本模型

本文所用的模型为钢圆柱以三角形排列植入空气中组成的二维二组元声子晶体，材料参数为：空气，ρ空气=1.29 ×10-3（kg·m-3），cl空气=0.34 ×103（m·s-1），ct空气=0（m·s-1）；钢柱，ρ钢=7.67 ×103（kg·m-3），cl钢=6.01 ×103（m·s-1），ct钢=3.23 ×103（m·s-1），其中ρ，cl，ct分别表示材料的质量密度，纵波波速和横波波速。钢柱的半径r=0.36（以晶格常数a为长度单位，下同），对应的单胞填充率为f=0.47。用多重散射方法计算模型能带结构及等频线，结果如图1所示。图1（a）中，从Γ点出发的直线表示空气的色散线。从图1（a）中可以看出，在频率0.62～0.95（归一化频率，下同）之间，Γ点的频率比其它点的频率都要高，说明该频段就是能发生负折射现象的频率区间［16］。图1（b）是等频线图，当频率达到0.62时，等频线凹向Γ点，与带结构图中的提示一致。

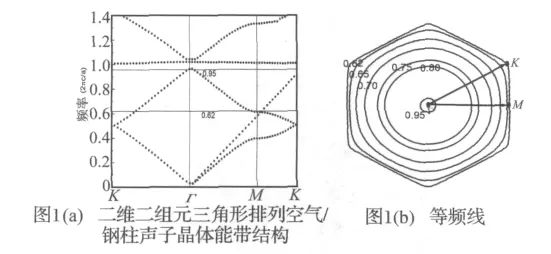
图1 Fig.1（a）Band structure two-dimensional two-component triangular arrangement steel/air phononic erystal（b）Equivalent frequency drawing

图1（b）显示，对于本文讨论的模型，在频段0.65～0.95之间，等频线的形状近似为圆形。这说明，在该频段内可用等效负折射率的概念来描述该声子晶体中的负折射行为，并可用neff=-k c/ω计算其等效负折射率［12］。本文所用声源的归一化频率为0.70，对应的等效负折射率为-0.54（下同）。

2 声子晶体平板单板成像

声子晶体平板负折射成像过程可用示意图2表示。图2中，d为声子晶体平板的厚度，点声源S到平板左表面距离为物距u，外部像到平板右表面的距离为像距v。点声源经平板两个表面折射后的像点分别成内部像点S0和外部像点S1。其中θi，θr分别代表入射角和折射角，平板的等效负折射率用neff表示。

根据反Snell定律及图中的几何关系可得，

当入射角θi较小时，利用近轴近似，表达式（1）、式（2）可简化为：

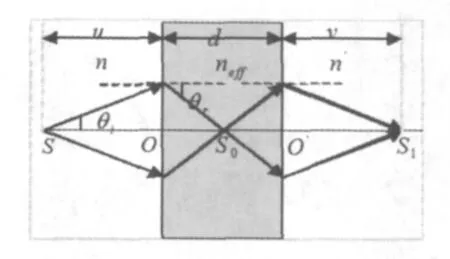
图2 负折射率声子晶体平板成像过程可用示意图Fig.2 Negative refractive index phononic crystal tablet imaging process available schematic diagram

从式（3）和式（4）可以看出：在近轴近似下，声子晶体平板内部像点S0的位置与声波的入射角θi、声子晶体平板的等效负折射率neff及声源离平板的距离u（即物距）有关，而与平板的厚度无关；而平板外部的像点S1，声波的入射角θi、声子晶体平板的等效负折射率neff及声子晶体平板的厚度有关，而与物距u无关。

图3、图4为声子晶体平板单板多重散射模拟的负折射成像图，图中白直线标记了平板的轮廓和像的中心位置。其中，图3（a）、（b）、（c）的物距保持不变，都为10.6。对应的平板厚度分别为11层、9层和5层。图3表明，这些不同厚度声子晶体平板内部的像点位置基本不变，符合式（3）的描述；平板外部的像点随着平板厚度的减少，离点声源的距离随之减少，符合式（4）描述。这说明声子晶体平板成像的‘宏观’过程可以用负的等效折射率和反Snell定律加以描述。需要特别指出的是，图3（c）中的平板的厚度几乎减少到了在一定物距下平板内部成像所需的最小厚度。图3中（a）、（b）、（c）对应的平板厚度分别为11层、9层和5层。

图3 物距相同（u=10.6），平板厚度不同的负折射成像。Fig.3 Negative refractive imaging with the same object distance（u=10.6）

图4 相同平板厚度（9层），不同物距下的负折射成像比较Fig.4 Negative refractive imaging with the same thickness

图4（a）、（b）、（c）中，平板厚度不变（都为9层板），对应的物距分别为 10.6，6.6 和 2.6。这表明，随着物距的减小，声子晶体平板内部的汇聚像点离平板入射面的距离随之减小，而平板外部的像点位置离平板出射面的距离则随之增大，但整个物像的距离基本保持不变，符合式（4）描述，即厚度一定时，物象之间的平板位置可以任意放置（但物距要在一定范围内，以保证平板内部有像点）。这一特性，可用平板折射只会平移出射波的位置，而不会改变声波的出射方向的性质来解释。进一步地，可以预见，一个厚平板的折射效果，可以用若干个薄平板的累积折射来等效，只要这些薄平板的厚度之和等于厚平板的厚度即可。图4中的（a）、（b）、（c）对应的物距分别为 10.6、6.6 和2.6。。

图3、图4说明，声子晶体单平板负折射成像可以用反Snell定律加以定量描述，可借用几何光学透镜成像的方法来分析。几何光学中，共轴多球面系统里实物实像、虚物虚像的复杂成像过程，是否也可以推广到声子晶体组合平板成像?为此，本文继续探讨组合平板成像的情况。

3 组合平板成像

以声子晶体双平板组成的透镜组为模型，讨论多平板声学透镜的成像情况。平板的结构和材料同前，声子晶体双板分别由7层板（以下称A板）和8层板（以下称B板）的钢/空气介质柱组成。模拟点声源经A、B双板后的成像情况。整个系统的物距为点声源（物点）到A板的距离，像距为系统右边像点到B板的距离。成像过程通过多重散射模拟，结果如图5中的左图所示。

图5（a）中，由于系统的物距适当，物点经A板后，在A、B两板之间成一实像；又因为A、B板的间距适当，A板所成的实像点成为B板的物点，经B板再折射后，得到系统最后的实像。整个成像过程可以用图5（b1）描述。其最后所成像的位置，也可多次利用式（3）、式（4），通过A、B板依次成像得到，类似于几何光学中多球面共轴系统的成像过程。图5（a1）的成像特点是：A、B板内部都有像点，整个系统实物成实像。

图5（a2）中，物距增大，A、B两平板的间距减小，这时，物点声波在入射A板左表面后，未来得及在A板内部汇聚，就从A板右表面折射出来了，相当于A板左表面实现了实物成实像，而右表面实现了虚物成虚像的过程；其后，声波很快以发散状进入B板，A板右表面的虚像成为B板左表面的实物，在B板中折射波会聚成B板内部的像点，再后，经B板右表面折射形成最后的实像点，即B板左、右表面都实现了实物成实像的过程。整个成像过程也可以用图5（b2）描述。同样地，也可多次利用式（3）、式（4），通过A、B板依次成像得到。图5（a2）的成像特点是：因系统物距过大，A板内部没有像点，但B板内部有像点，整个系统实物成实像。

图5 声子晶体双平板成像Fig.5 Phononic crystal twin slabs imaging

图5（a3）的成像存在类似的依次成像的组合成像规律。图5（a3）中，物距合适，A板内部有实像点，但A、B板的间距很短，这使得B板太靠近A板，在A板的出射波成实像之前，声波就碰到了B板。负折射平板界面总是使折射波的发散/会聚状与入射波的会聚/发散状态相对应，因而提供了成实像的可能。这一点非常不同于正常折射的光学平板界面。正常折射的光学平板界面，折射波只是继承入射波的聚散特征，而不会改变聚散特征。图5（a3）中，当声波经A板后，以会聚状进入B板时，在B内声波就呈发散状，B板内部没有像点，但经B板右表面出射后，又能会聚成实像。整个系统也实现了实物成实像的过程。图5（a3）成像特点是：A板内部有像点，B板内部没有像点，整个系统还是实物成像。

图5（a4）中，A板由于物距过大，声波在板内会聚之前就遭遇右表面折射出射，A板整体呈实物成虚像的过程。A板的虚像成为B板的实物，但A、B两平板间的距离过长，B板成像时的物距仍然过大，B板成像类似于A板，也呈实物成虚像的过程。因此，图5（a4）的成像特点是：因系统物距过大，A板、B板两板单独成像时的物距都过大，都是实物成虚像，两平板内部都没有像点存在，虽然各个折射面都有明显的负折射行为发生，但整个系统也没有最后形成实像。

根据物像式（3）、式（4），按照成像的顺序，对图5中的各次成像的物距、像距进行计算，得到系统最后的物距、像距的理论计算值，并与多重散射模拟成像图中直接读出的物像数据进行比较，结果见表1。表1表明：在引入等效折射率后，利用反Snell定律的近似理论计算值和多重散射成像图中的直读值基本一致。数据的些许差异与近轴近似和读数误差有关。

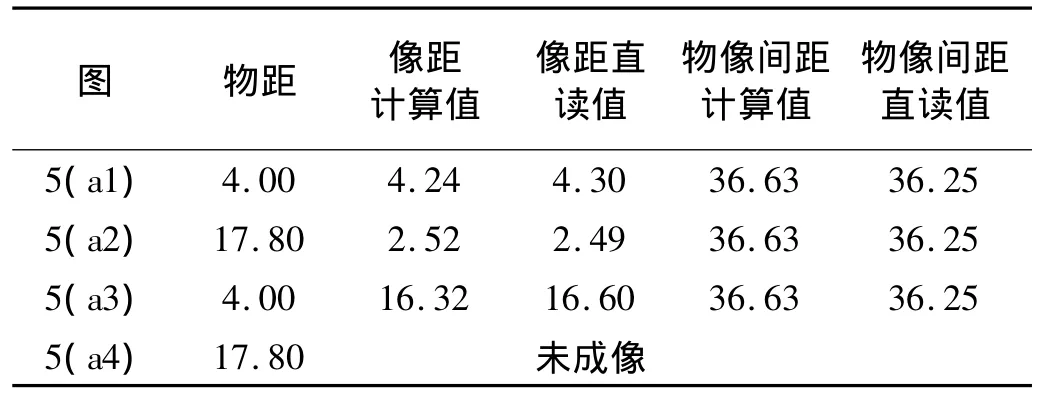
表1 理论计算值与成像直读值比较Tab.1 Theoretical calculation and imaging direct-read value comparison

对图5和表1的分析说明，声子晶体平板多板系统成像，符合依次成像的规律，可借用几何光学多球面共轴系统中实（虚）物、实（虚）像的类似的复杂过程来进行分析。每次折射从理论上都可以用反Snell定律进行定量的描述。同时，由于平板透镜系统的折射面是平面，入射波经平板折射后，无论是正常折射还是负折射，出射波相对于入射波只是平移了位置，不改变方向。因此，图5（a1）、（a2）、（a3）中，A、B 板相同，尽管A、B板在物象之间摆放的位置不一样，但只要能成实像，总的物像距离保持不变（见表1）。这一结论在图6中得到进一步证实。

图6显示了15层厚的单板与等厚度的多个薄板组成的系统的成像情况。其中，图6（a）为三个5层平板（即每板由5层介质柱形成的平板）组合而成的透镜系统的成像情况；图6（b）为7层板和8层板两个平板组合的成像情况；图6（c）为单个15层板的成像情况。点声源经过这些平板数不同但总厚度相同的系统后，都能成像，而且物像间距相同。平板透镜的这一性质在调节物距、像距和摆放平板透镜方面提供了更多的灵活性。在平板摆放受空间限制时，这一特点就显出优势来。

图6 等厚度的平板组合成像的比较Fig.6 Combination tablet imaging comparison with the same thickness

4 结论

本文以二维钢圆柱/空气三角排列声子晶体为模型，分析了声子晶体平板透镜的成像特性。结果显示，在特定频率范围内，声子晶体平板可以用作独立的声平板透镜，利用负折射效应成像；平板透镜在引入等效负折射率后，其成像服从反Snell定律，可以解析表达；多平板组合系统成像服从依次成像规律，可借用几何光学中的多球面共轴系统成像的方法、引入实（虚）物实（虚）像的概念来分析；无论正常折射还是负折射，虽然在平板内部声波都是折射的，但整体上看，入射平板的声波和出射平板的声波，方向相同，只是出射波的位置相对入射平板的位置有一个平移，且平移的距离与平板的厚度有关；正常折射因入射线和折射线分列法线两侧而不能成像，负折射因入射线和折射线列法线同侧而能成像；在总厚度不变的情况下，单平板透镜和多平板透镜的最终成像效果相同，这一性质虽然给多平板透镜的摆放提供了一些方便，但多个平板亦须有适当的位置关系，才可取得等厚度单板成像相同的效果。多重散射看似无规的过程，在声子晶体周期结构的调制下，表现出了足够的规律性来。声子晶体负折射，实际上是特定的声子晶体平板，对声波进行多重散射的特殊结果。在引入等效负折射率后，声子晶体平板成像过程的描述，也变得简单和容易掌握。平板成像的其它性质及影响因素有待进一步的研究。

［1］Veselago V G.The electrodynamics of substances with simultaneous negative values ofεandμ［J］.Soviet Physics Uspekhi，1968，10（4）：509-514.

［2］ Pendry J B，Holden A J，Stewart W J，et al.Extremely low frequency plasmons in metallic meso structure［J］.Phys.Rev.Lett，1996，76（25）：4773-4776.

［3］ Pendry J B，Holden A J，Robbins D J，et al.Mag-netism from conductors and enhanced nonlinear phe-nomena［J］.IEEE Trans.Microwave Theory Tech.，1999，47（11）：2075-2084.

［4］ Smith D R，Padilla W J，Vier D C，et al.Composite medium with simultaneously negative permeability and permittivity［J］.Phys Rev Lett，2000，84（18）：4184-4187.

［5］ Shelby R A，Smith D R，Schultz S.Experimental verification of a negative index of refraction［J］. Science，2001，292（5514）：77-79.

［6］Notomi M.Theory of light propagation in strongly modulated photonic crystals：refraction like behavior in the vicinity of the photonic band gap［J］.Phys.Rev.B，2000，62（16）：10696-10705.

［7］ Moussa R，Foteinopoulou S，Zhang L，et al.Negative refraction and superlens behavior in a two-dimensional photnic crystal［J］. Phys. Rev. B， 2005，71（8）0851061-0851065.

［8］Feng L，Liu X P，Lu M H，et al.Acoustic backward-wave negative refractions in the second band of a sonic crystal［J］.Phys.Rev.Lett.，2006，96（1）：0143011-0143014.

［9］Zhang Y，Fluegel B，Mascarenhas A.Does optical anisotropy lead to negative refraction at an interface［J］.Phys.Rev.Lett，2003，91：157404.

［10］ Zhang X D.Universal non-near-field focus of acoustic waves through high-symmetry quasicrystals［J］.Phys，Rev.B，2007，75：024209.

［11］ Sukhovich A，Li J，Page J H.Negative refraction and focusing of ultrasound in 2D phononic crystals［J］.Phys，Rev.B，2008，77（014301）：1-9.

［12］ Li J，Chan C T.Double-negative acoustic metamaterial［J］.Phys.Rev.E，2004，70（5）：0556021-0556024.

［13］ Pendry J B.Negative refraction makes a perfect lens［J］.Phys Rev Lett，2000，85（18）：3966-3969.

［14］Qiu C Y，Zhang X D，Liu Z Y.Far-field imaging of acoustic waves by a two-dimensional sonic crystal［J］.Phys.Rev.B，2005，71（5）：0543021-0543026.

［15］李晓春，高俊丽，刘绍娥，等.二维声子晶体平板成像中的通道特征［J］.物理学报，2010，59（1）：376-380.

［16］ Li S，Thomas F G，Chen L S，et al.Disorder effect on the focus image of sonic crystal in air［J］.Phys.Rev.E，2006，73（5）：0566151-0566154.