飞行管理系统水平引导过渡路径构建算法

庞 寅，章卫国，李广文

（西北工业大学自动化学院，西安 710027）

飞行水平引导是飞行管理系统的重要功能之一。为了实现飞行引导功能，必须要有完整的引导路径。然而，对ARINC424编码解析得到的航段可能存在折线过渡、航向突变、航段不连续等问题，各航段间必须建立平滑的过渡路径，才能生成合理的引导路径。因此过渡路径的建立是实现水平引导的关键技术之一。同时，并非所有航段间都可以平滑过渡，在某些情况下，就会出现非常特殊的“fish-bird”类型。若无法解决“fish-bird”类型的过渡问题，也无法得到平滑的引导路径。针对上述问题，首先给出建立过渡路径的方法，并在此基础上给出“fish-bird”类型的过渡问题解决方案，最后提出了航段间建立过渡路径的完整流程。

1 飞行计划中的航段类型及其过渡路径

1.1 航段类型简介

在ARINC424中，按照起点和终点的不同划分了23种不同类型的航段，常用的航段类型如表1所示。

1.2 航段间的不同过渡类型

ARINC424编码逐行进行解析，航段的过渡也逐航段进行分析，这样有利于实现计算机自动解析。在ARINC424中，共有6种不同情况的过渡类型。

1）切线过渡，如图 1 所示。要求已知 Pi、Pm、Pn3 个航路点，一般为2航段以直线相交于Pm点，这时就需要一段圆弧进行平滑过渡。

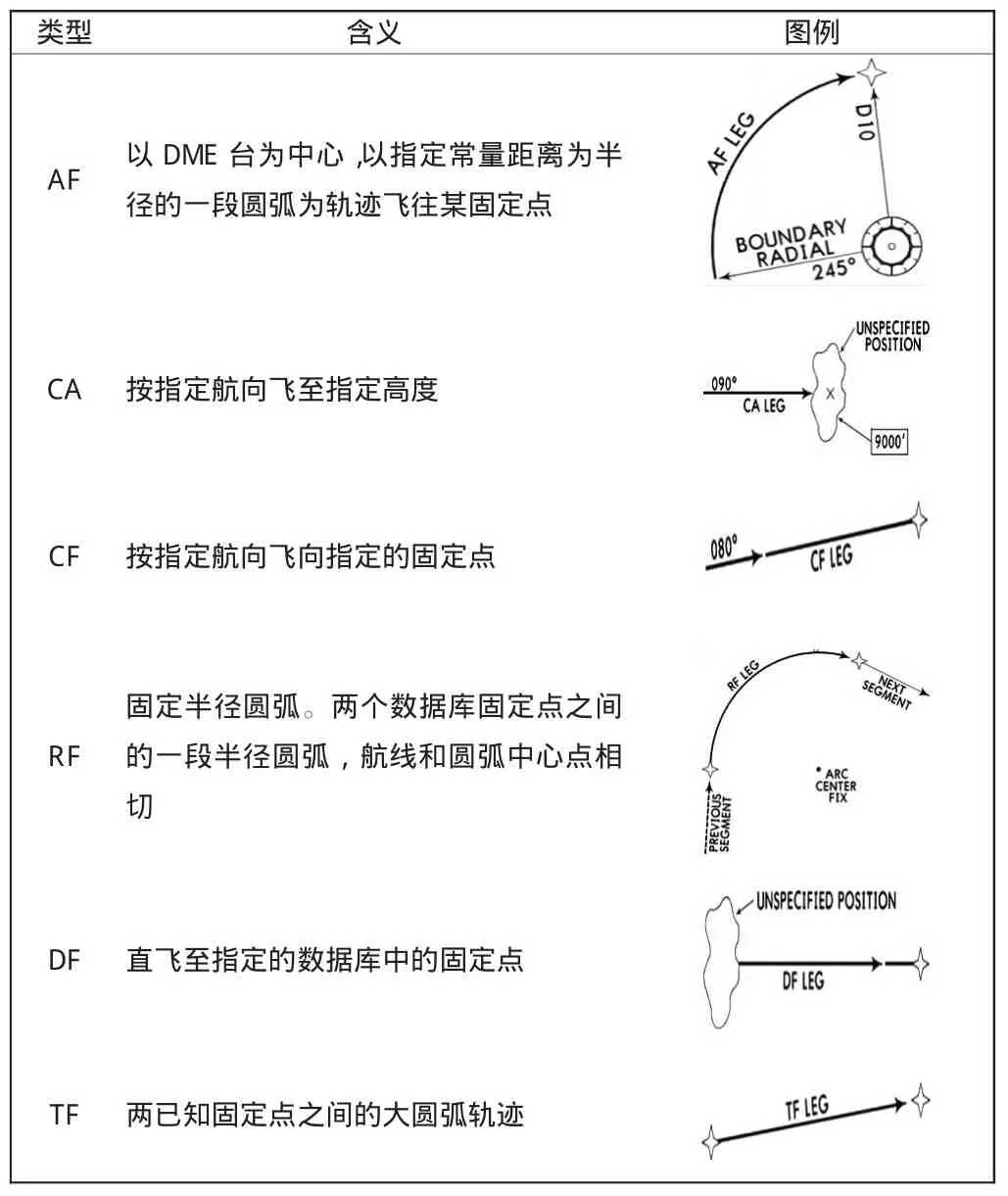
表1 ARINC424中常用的航段类型Tab.1 Common leg types in ARINC424

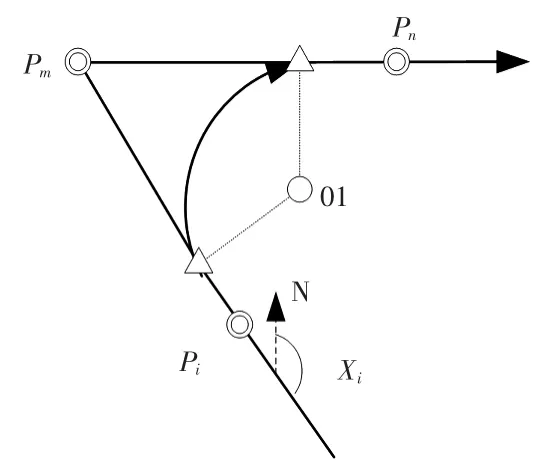
图1 切线过渡Fig.1 Tangent transition

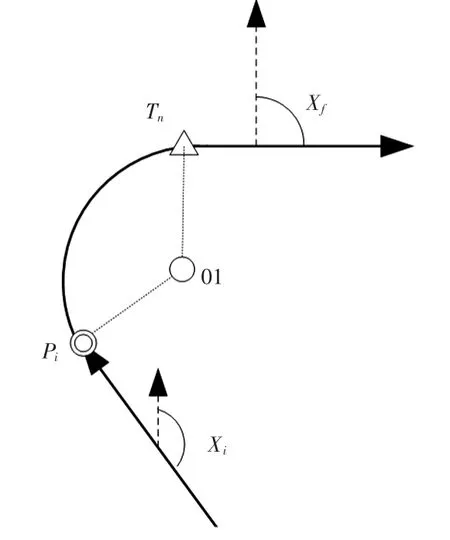
图2 方位截获Fig.2 Position interception

2）方位截获，如图2所示。当前航段要求已知航向角Xf。

图 3 45°截获Fig.3 45°interception

3）45°截获，如图3所示。当前航段要求已知航路点Pn、航向角Xf。飞机先以方位截获到与Xf夹角45°的航线上，再以切线过渡到下一航段。

4）直飞过渡，如图4所示。当前航段要求已知航路点 Pn。

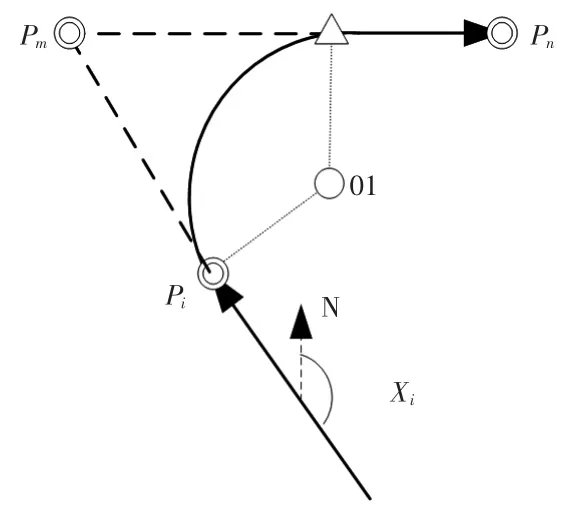
图4 直飞过渡Fig.4 Direct transition

5）圆弧过渡，如图5所示，已知航段终止时飞机的航向角Xi、航段终止点Pi的坐标、当前航段航路点Pm、Pn、过渡圆弧圆心 O1、过渡半径 R，当前航段为一段圆弧。

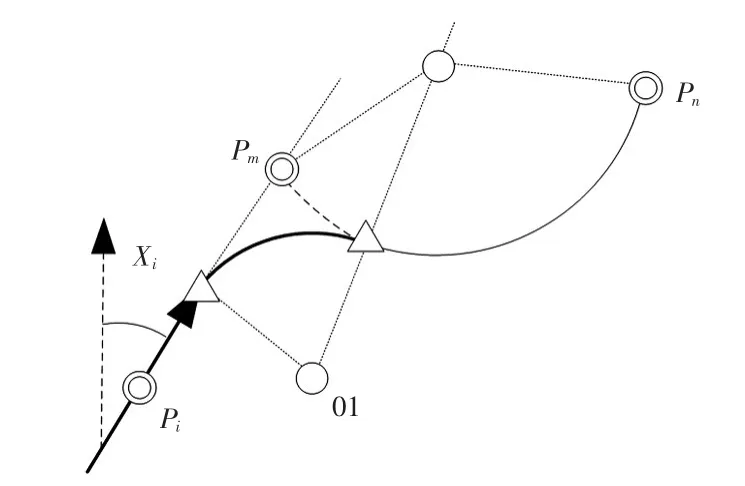
图5 圆弧过渡Fig.5 Arc interception

6）等待，如图6所示，已知航段终止时飞机的航向角Xi、航段终止点Pi的坐标、当前航段航路点Pn。当前航段为等待程序。

其中，航段终止时飞机的航向角、航段终止点由解析过的航段给出，当前航段信息都由飞行计划给出，直接从ARINC424编码解析的结果提取所需信息。过渡半径r已知。

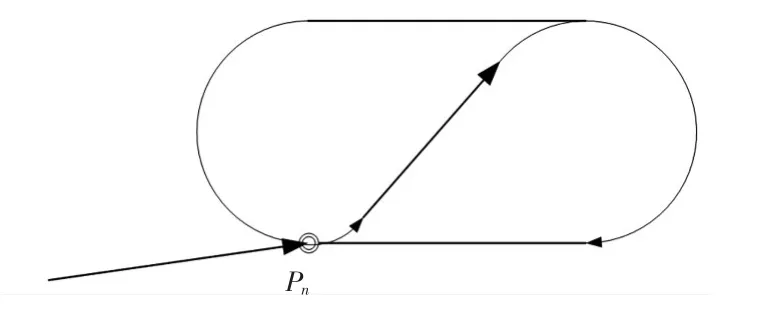
图6 等待Fig.6 Holding

根据过渡路径给出的已知条件，可通过几何解析得到过渡路径空间几何信息，包括过渡圆弧半径，圆心以及过渡起始点和终止点。

在圆弧过渡和进入等待程序时，要求飞机直飞向当前航段要求航路点。因此在前一航点终止后，需要通过直飞过渡直飞向当前航段要求航路点，再进入圆弧过渡或等待。

2 特殊过渡路径

2.1 fish-bird类型介绍

当航段都足够长时，生成的引导路径中连续、平滑过渡路径可以实现，过渡路径之间不会冲突。但当支路比较短或夹角大于90°时，易出现非连续路径，如图7、图8所示。这就要求将这些特殊路径处理得到合理的可飞路径，以实现引导路径的自动生成。图7中过渡路径AB超过了支路L2的终点，这种情况称为“fish”。在这种情况下正常方法无法计算L2到L3的过渡路径。图8中过渡路径AB终止点B超过了过渡路径CD的起始点C，这种情况称为“bird”。在这种情况下飞机需要从B点倒飞到C点才能完成过渡，这是不合理的。这2种特殊路径合称为“fish-bird”。

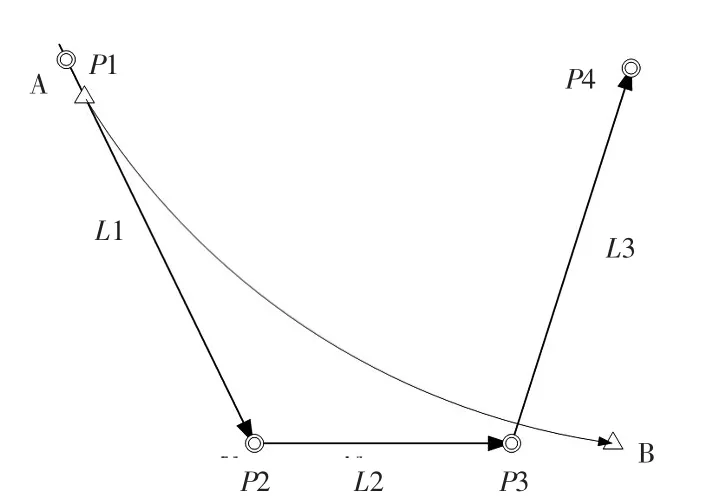
图7 “fish”类型Fig.7 Type of“fish”

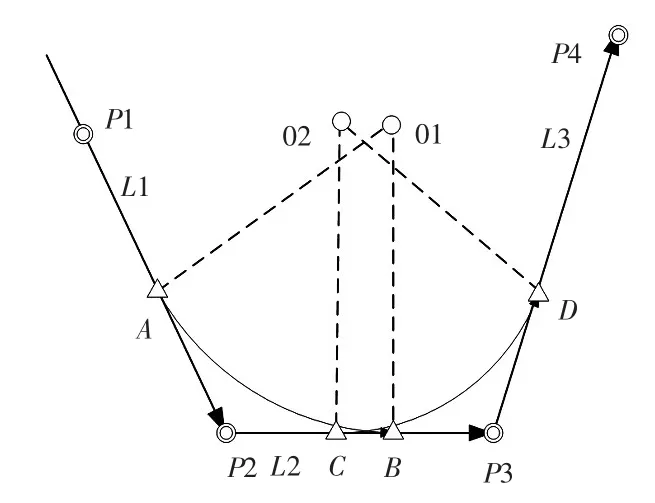
图8 “bird”类型Fig.8 Type of“bird”

2.2 fish-bird类型的判断

如 L1、L2、L3为 3 个连续航段，L1航段过渡到 L2航段时，根据已知的P1、P2、P3点经纬度坐标，转弯半径可解出过渡圆弧的起始点A、终止点B的经纬度坐标，如图9所示。

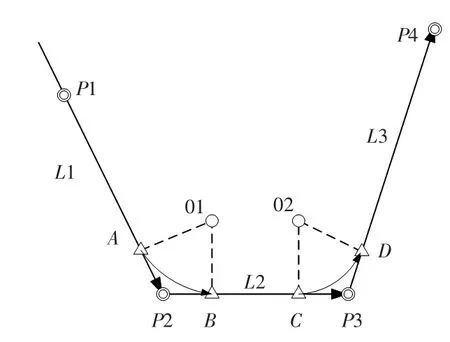
图9 特殊路径判断Fig.9 Judgemeng of special transition

1）判断过渡终止点B与L2航段终止点P3之间的相对位置。首先根据B、P2、P3点经纬度计算出B点到 P2点的距离｜BP2｜、B 点到 P3点的距离｜BP3｜、P2点到P3点的距离｜P2P3｜。若｜BP2｜< ｜P2P3｜且｜BP3｜< ｜P2P3｜，则说明过渡路径未超过了航段终点，否则出现“fish”类。

2）若过渡路径未超过航段终点，继续解析L2航段到L3航段的过渡路径，根据已知的P2、P3、P4点经纬度坐标，转弯半径可解出过渡圆弧的起始点C、终止点D的经纬度坐标，这时，判断L1、L2航段过渡终止点B与L2、L3航段过渡起始点C之间的相对位置。首先根据B、C、P3点经纬度计算出 B 点到 C 点的距离｜BC｜、B点到 P3点的距离｜BP3｜、C 点到 P3点的距离｜CP3｜。若｜BC｜< ｜BP3｜且｜CP3｜< ｜BP3｜，则不出现特殊过渡路径，可以正常过渡；否则出现“bird”类型。

2.3 fish-bird类型的过渡处理

由fish-bird类型的判断过程可知，2种特殊路径的出现都是由于L2太短造成的，这时可舍弃L2航段，由L1航段直接过渡到L3航段。2种特殊路径的不同在于“fish”类型特殊路径在L1过渡到L2时出现的，这是舍弃L2航段，相当于舍弃了当前航段。而“bird”类型特殊路径在L2过渡到L3时出现的，这是舍弃L2航段，相当于舍弃了前一航段。

3 航段过渡解析流程

3.1 过渡类型的选择

根据当前航段的要求不同，结合前文中介绍的不同过渡类型的要求已知条件不同，可以把过渡类型的选择归纳如下：

1）当前航段给定航向角时，采用方位截获；

2）当前航段给定航路点时，采用直飞过渡；

3）当前航段给定航路点和航向角时，由于45°截获当前航段要求已知航路点、航向角，因此可采用45°截获；

4）过渡时两条直线支路相交，采用切线过渡；

5）当前航段为一段圆弧时，先直飞向当前航段要求航路点，然后采用圆弧过渡；

6）当前航段为HA航段、HF航段或HM航段时，先直飞向当前航段要求航路点，然后进入等待程序。

3.2 过渡解析流程

航段间过渡路径解析流程如图10所示。

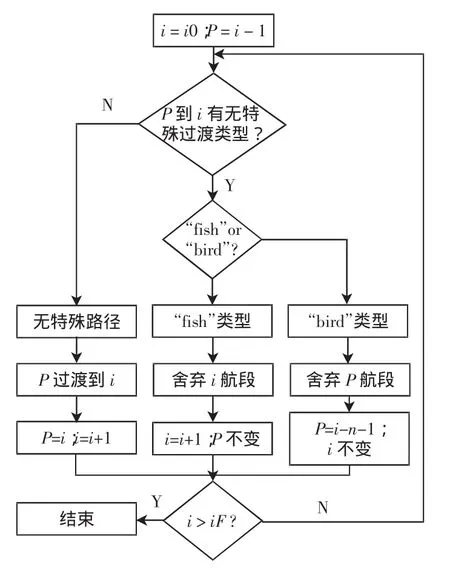
图10 航段过渡解析流程Fig.10 Analyzing process of flight plan

图中，i表示当前航段序号；P是指前一未舍弃航段的序号；i0表示起始航段；n指连续跳过航段的个数。

解析流程如下：

初始化 i=i0，P=i-1；

For i=1：n

If P航段能正常过渡到i航段

建立P航段到i航段的过渡路径（过渡类型选择由上文 3.1给出）P=i，i+1

Else

If出现“fish”类型特殊路径

舍弃i航段，i+1

Else出现“bird”类型特殊路径

舍弃P航段，P=i-n-1

End

End

4 仿真验证

对如表2中所列飞行计划进行解析，飞机初始位置为[36，110]，起始航向角为340°。将和航段解析最关键的飞行计划信息列出，如表2所示。

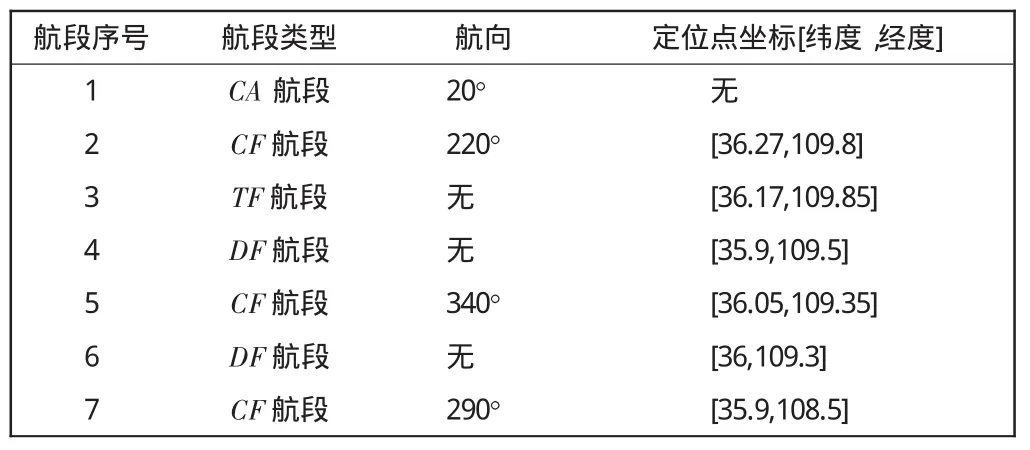
表2 飞行计划航段关键信息提取Tab.2 Key information of flight plan

1）从CA航段开始解析，起始航向与CA航段要求航向不同，因此应采用方位截获过渡到CA航段的要求航向角20°，爬升到指定高度CA航段结束。

2）第2段航段为CF航段，要求航向角合航路点坐标，根据前文中给出的方式判断可采用切线过渡，到达CF航段指定定位点[36.27，109.8]，CF航段结束。

3）在从CF航段过渡到TF航段时，为两直线支路相交，采用切线过渡，但经判断出现“bird”类型路径，因此舍弃第2段航段CF航段，再从CA航段直接过渡到TF航段，采用切线过渡，到达TF航段航路点[36.17，109.85]，TF 航段结束。

4）TF航段过渡到DF航段时，采用直飞过渡，经判断出现“bird”类型路径，因此舍弃第3段航段TF航段；再从CA航段直接过渡到DF航段，采用直飞过渡，到达DF航段指定航路点[35.9，109.5]，DF航段结束。

5）DF航段过渡到CF航段时，经判断可以采用切线过渡，采用切线过渡过渡到CF航段，到达CF航段指定定位点[36.05，109.35]，CF航段结束。

6）CF航段过渡到DF航段时，过渡类型选择直飞过渡，经判断出现“fish”类型路径，舍弃第6段航段DF航段。

7）从第5段航段CF航段过渡到第7段航段CF航段时，经判断无法使用切线过渡，因此采用45°截获过渡，到达CF航段指定定位点[35.9，108.5]，CF航段结束。至此解析完毕。

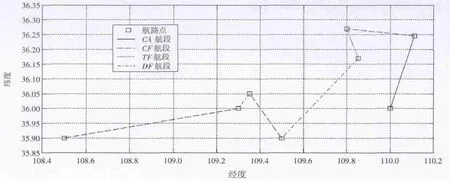
图11 解析前飞行计划路径Fig.11 Flight plan path before analyzing process

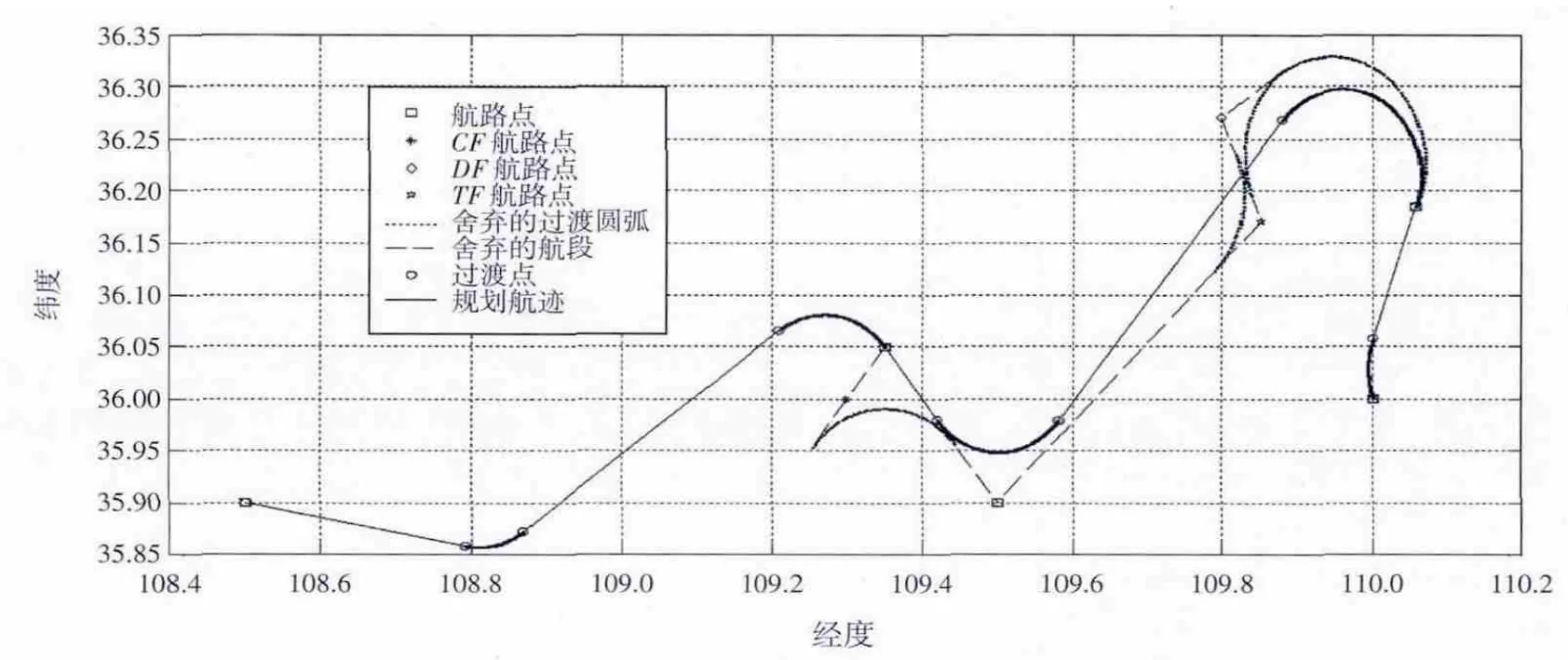
图12 路径过渡解析结果Fig.12 Simulation of analyzing process

图11是解析前飞行计划路径。路径过渡解析仿真结果如图12所示。仿真结果说明解析流程可解决航段过渡问题，证明了解析流程的可行性，同时算例中出现了连续fish-bird类型路径，该流程也可有效解决。

5 结语

针对水平引导航段间平滑过渡的问题，首先介绍了航段间的不同过渡类型，然后重点分析了“fishbird”路径的问题。先介绍问题的出现，接着进行分析判断，并给出解决方案。最后将特殊路径的问题与航段正常过渡的问题进行总结归纳为过渡类型的选择问题，并给出完整的解析流程。应用所研究理论，可在所有航段间建立平滑可飞的过渡路径，为水平引导功能的实现提供了理论支持。

[1]Specification A.424-16 Navigation System Database[S].2002.

[2]RTCA（Firm）.SC-181.Minimum Aviation System Performance Standards：Required Navigation Performance for Area Navigation[S].RTCA，2000.

[3]BARHYDT R，WARREN A W.Development of Intent Information Changes to Revised Minimum Aviation System Performance Standards for Automatic Dependent Surveillance Broadcast（RTCA/DO-242A）[M].National Aeronautics and Space Administration，Langley Research Center：2002.

[4]宋 柯.ARINC424终端区程序编码解析与轨迹还原[J].空中交通管理，2010（8）：50-53.

[5]王 军，杨 辉，蒋志锋.民航导航数据库国内数据更新技术研究——实现国内导航数据的ARINC424编码与整合[J].空中交通管理，2009（5）：23-26.

[6]KLOOSTER J，TORRES S，EARMAN D，et al.Trajectory Synchronization and Negotiation in Trajectory Based Operations[C].Digital Avio-nics Systems Conference（DASC），2010 IEEE：A.3-11.

[7]TORRES S，DELPOME K L.An integrated approach to air traffic management to achieve trajectory based operations[C]//Digital Avionics Systems Conference（DASC），2012 IEEE/AIAA 31st.IEEE，2012：3E6-1-3E6-16.